벡터 메손

가벼운 쿼크로 구성된 벡터 메손은 노넷을 형성한다.

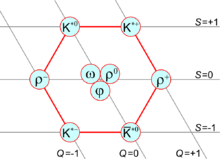
고에너지 물리학에서 벡터 메손은 총 스핀 1과 홀수 패리티(일반적으로 J^P = 1⁻)를 갖는 메손이다.벡터 메손은 1960년대 이후 실험에서 볼 수 있었으며, 질량의 분광 패턴으로 잘 알려져 있다.^[1]

벡터 중간자는 전체 스핀 1을 갖지만 그 대신 짝수 패리티를 갖는 유사벡터 중간자와 대조된다.벡터 메손과 유사 메손은 벡터 메손의 분광법이 거의 순수한 구성 쿼크 맛의 상태를 보여주는 경향이 있는 반면 유사 메손과 스칼라 메손은 혼합 상태의 복합체로 표현되는 경향이 있다는 점에서 또한 다르다.

고유하게 순수한 맛 상태

머레이 겔만(그리고 조지 즈바이그에 의해서도 독립적으로)에 의한 쿼크 모델의 개발 이후 벡터 메손은 순수 상태의 분광법을 실증해 왔다.^[2]^[3]^[4]The fact that the $I$ = 1 rho meson (ρ) and $I$ = 0 omega meson (ω) have nearly equal mass centered on 770–780 MeV/c², while the phi meson (φ) has a higher mass around 1020 MeV/c², indicates that the light-quark vector mesons appear in nearly pure states, with the φ meson having a nearly 100 percent amplitude of hidden strangeness.

벡터 중간자 특성의 이러한 거의 순수한 상태는 가성 중자 또는 스칼라 중자 다중자에서는 전혀 명백하지 않으며, 텐서 중자와 유사 중자 다중자 사이에서만 약간만 실현될 수 있다.이 사실은 벡터 중간자를 다른 유형의 벡터 중간점으로 비벡터 중간자의 각각의 붕괴율을 통해 측정된 다른 유형의 중간체의 쿼크 맛 함량에 대한 훌륭한 탐사로 만든다.이러한 실험은 혼합된 주 중간의 맛을 결정하려는 이론가들에게는 매우 명백하다.

중원 분광학의 백본

더 높은 질량에서 벡터 중간은 그들의 구조에 매력과 바닥 쿼크를 포함한다.이 영역에서는 복사 과정이 두드러지는 경향이 있는데, 광자 방출에 의해 중텐더와 스칼라 중간자가 주로 벡터 중간체로 부패한다.유사 공정에서 유사 공정의 유사성 중수로의 전환.헤비 메손의 스펙트럼의 많은 부분이 벡터 메손에 복사 작용에 의해 묶여 있기 때문에, 일반적으로 벡터 메손의 분광에 대한 일종의 백본을 형성하는 것으로 생각할 수 있다.

일부 벡터 메손은 다른 메손에 비해 매우 높은 정밀도로 측정할 수 있다.이는 그들이 광자, 즉^PC J = 1과⁻⁻ 동일한 양자수를 가지고 있다는 사실에서 비롯된다. 여기서 J = 각운동량 양자수, P = 패리티, C = 패리티.따라서 전자-양전자 충돌에서 $e^{-}e^{+}\to \gamma \to q{\bar {q}}$ - $e^{-}e^{+}\to \gamma \to q{\bar {q}}$ + → $e^{-}e^{+}\to \gamma \to q{\bar {q}}$ → $e^{-}e^{+}\to \gamma \to q{\bar {q}}$ 의 $e^{-}e^{+}\to \gamma \to q{\bar {q}}$ 의 $q$ 의 q $.{-}e^{+}\to \bar{q}}$ 에 나타나는데 $e^{-}e^{+}\to \gamma \to q{\bar {q}}$ 이는 hadronic 프로세스를 사용해야 하는 다른 측정에 비해 실험적으로 명확한 신호를 제공한다.벡터 메손은 강한 해드론 힘을 연구하는 데 큰 역할을 한다.

벡터 중간자 목록

가상의

메손

참고 항목

참조

^ Nichitiu, F. (November 2, 1995). "An Introduction to the Vector Meson" (PDF). Retrieved June 1, 2021.
^ Gell-Mann, M. (4 January 1964). "A Schematic Model of Baryons and Mesons". Physics Letters. 8 (3): 214–215. Bibcode:1964PhL.....8..214G. doi:10.1016/S0031-9163(64)92001-3.
^ Zweig, G. (17 January 1964). An SU(3) Model for Strong Interaction Symmetry and its Breaking (PDF) (Report). CERN Report No.8182/TH.401.
^ Zweig, G. (1964). An SU(3) Model for Strong Interaction Symmetry and its Breaking: II (PDF) (Report). CERN Report No.8419/TH.412.

이 입자물리학 관련 기사는 단조롭다.위키피디아를 확장하여 도울 수 있다.

[1] Nichitiu, F. (November 2, 1995). "An Introduction to the Vector Meson" (PDF). Retrieved June 1, 2021.

[2] Gell-Mann, M. (4 January 1964). "A Schematic Model of Baryons and Mesons". Physics Letters. 8 (3): 214–215. Bibcode:1964PhL.....8..214G. doi:10.1016/S0031-9163(64)92001-3.

[3] Zweig, G. (17 January 1964). An SU(3) Model for Strong Interaction Symmetry and its Breaking (PDF) (Report). CERN Report No.8182/TH.401.

[4] Zweig, G. (1964). An SU(3) Model for Strong Interaction Symmetry and its Breaking: II (PDF) (Report). CERN Report No.8419/TH.412.

[1]

[2]

[3]

[4]

Search

벡터 메손

네임스페이스

더

목차

고유하게 순수한 맛 상태

중원 분광학의 백본

벡터 중간자 목록

가상의

참고 항목

참조