총계
Summation| 산술 연산 | ||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||
수학에서, 덧셈은 덧셈 또는 덧셈이라고 불리는 모든 종류의 숫자의 수열을 더하는 것이다; 그 결과는 그들의 합 또는 합계이다.숫자 외에도, 함수, 벡터, 행렬, 다항식, 그리고 일반적으로 "+"로 표시된 연산이 정의된 모든 유형의 수학적 객체의 요소 등 다른 유형의 값들도 합산될 수 있다.
무한 수열의 합계를 급수라고 합니다.이러한 개념에는 한계라는 개념이 포함되며 이 문서에서는 다루지 않습니다.
명시적 수열의 합계는 일련의 덧셈으로 나타난다.예를 들어 [1, 2, 4, 2]의 합은 1 + 2 + 4 + 2로 표시되고 9가 됩니다. 덧셈은 연관성과 가환성이 있기 때문에 괄호가 필요하지 않으며 결과는 합산의 순서에 관계없이 동일합니다.하나의 요소만으로 이루어진 시퀀스를 합하면 이 요소 자체가 됩니다.관례상 빈 시퀀스(원소가 없는 시퀀스)의 합계는 0이 됩니다.
대부분의 경우 시퀀스의 요소는 규칙적인 패턴을 통해 시퀀스 내의 각 요소의 함수로 정의됩니다.단순한 패턴의 경우 긴 시퀀스의 합계는 대부분의 합계가 타원으로 대체되어 표현될 수 있다.예를 들어, 처음 100개의 자연수의 합계는 1 + 2 + 3 + 4 + 99 + 99 + 100으로 쓸 수 있습니다.그렇지 않으면 δ 표기법을 사용하여 합계를 나타냅니다. 여기서δ {은 대문자 그리스 문자 시그마입니다.예를 들어, 첫 번째 n개의 자연수의 합은 . { _}^{로 표시될 수 있다.
긴 합계 및 가변 길이의 합계(타원 또는 δ 표기로 정의)의 경우, 결과의 닫힌 형식의 식을 찾는 것은 일반적인 문제입니다.예를 들어,[a]
이러한 공식들이 항상 존재하는 것은 아니지만, 많은 합계 공식들이 발견되었으며, 이 문서의 나머지 부분에는 가장 일반적이고 기본적인 공식들이 나열되어 있습니다.
표기법
대문자 시그마 표기법
수학 표기법은 많은 유사한 용어의 합계를 간략하게 나타내는 기호를 사용합니다. 즉, 그리스 문자 시그마의 확대된 형태인 합계 기호 δ \입니다.이것은 다음과 같이 정의됩니다.
여기서 i는 합계의 지수, a는i 합계의 각 항을 나타내는 지수 변수, m은 합계의 하한, n은 합계의 상한입니다.합산 기호 아래의 "i = m"은 지수 i가 m과 동일하게 시작됨을 의미한다.지수 i는 연속항마다 1씩 증가하며 i = [b]n일 때 멈춘다.
이것은 "ii = m에서 n까지의 a의 합"으로 읽힌다.
다음으로 제곱의 합계를 나타내는 예를 나타냅니다.
반면 어떤 변수 가중( 없는 모호성 발생된다 제공되)들이 가장 흔한 예가의 인덱스로 사용될 수 있는 그런으로 ,[c]j{j\displaystyle}, k{k\displaystyle}, n의{n\displaystyle}{\displaystyle 나는}일반적으로, 후자 또한 종종 summatio의 상한에 사용되는 편지를 포함한다.n.
또는 맥락이 충분히 명확할 경우 합계의 정의에서 지수와 한계가 생략되는 경우가 있다.이는 특히 지수가 1에서 [1]n까지 실행될 때 적용됩니다.예를 들어 다음과 같이 쓸 수 있습니다.
이 표기법의 일반화는 종종 사용되며, 임의의 논리 조건이 제공되며, 그 조건을 만족시키는 모든 값에 대해 합계를 취하도록 의도되어 있습니다.예를 들어 다음과 같습니다.
는 된 범위의 모든 kk에 대한 f의 (\\sum _99))의 (의 대체 표기법입니다.유사하게,
의 모든 x에 대한f {f의 입니다.
는n[d]n을 모든 의 정수 d d의 입니다.
또한 많은 시그마 부호의 사용을 일반화하는 방법도 있습니다.예를들면,
와 같다
시퀀스의 곱에도 같은 표기법이 사용됩니다.여기서 그리스 대문자 파이(pi)의 확대형식인 는 대신 사용됩니다.
특수한 경우
2개 미만의 숫자를 합산할 수 있습니다.
이러한 퇴화 케이스는 보통 특별한 경우에서 퇴화 결과를 합산 표기법에 의해 제공할 때만 사용됩니다.예를 들어 위의 정의에서 n { n=이면 합계에 항이 하나뿐이고, -1 { n이면 항이 없습니다.
형식적 정의
합계는 다음과 같이 재귀적으로 정의할 수 있습니다.
- δ i g( i ) \0 b < a;의 경우
- a g( )g ( b ) +∑ = - g( i ){ \i)+\a}^{ig(i)}(i) (b)의 경우 bg(i)입니다.
측정 이론 표기법
측정과 적분 이론의 표기법에서, 합은 확실한 적분으로 표현될 수 있다.
서a[ , b { [ a , b는 ~의 서브셋이며,μ { \ \는 카운트 측도입니다.
유한차이의 미적분
[m, n] 구간의 정수에 대해 정의된 함수 f가 주어지면 다음 방정식이 성립한다.
이것은 유한 차이의 미적분학에서 미적분학의 기본 정리의 유사체이다.
어디에
f의 도함수입니다.
위의 방정식의 적용 예는 다음과 같습니다.
위의 공식은 다음과 같이 정의되는 연산자 \Delta 의 반전에 더 일반적으로 사용됩니다.
여기서 f는 음이 아닌 정수에 정의된 함수입니다.따라서 이러한 함수 f가 주어지면 F = F F= ( + ) F ( \\ F의 역차별을 하는 것이 문제입니다} 이 함수는 상수의 덧셈까지 정의되며 다음과 같이 선택할[2] 수 있다
이러한 합계에 항상 닫힌 형식 식이 있는 것은 아니지만, Faulhaber의 공식은 f() n {\f(n)= k}인 경우 그리고 선형에 의해 n의 모든 다항식 함수에 대해 닫힌 형식을 제공한다.
일정한 적분에 의한 근사
이러한 많은 근사치는 증가 함수 f에 대해 유지되는 합계와 적분 사이의 다음과 같은 연결을 통해 얻을 수 있다.
그리고 모든 감소 함수 f:
좀 더 일반적인 근사치에 대해서는 오일러-매클로린 공식을 참조한다.
지수의 적분 가능한 함수에 의해 합계가 주어지는(또는 보간될 수 있는) 합계의 경우, 합계는 대응하는 확정 적분의 정의에서 발생하는 리만 합계로 해석될 수 있다.따라서 예를 들어 다음과 같은 것을 기대할 수 있다.
오른쪽은 정의상 왼쪽의 n n n {\ \ n \ \에 한계이기 때문입니다.그러나, 주어진 합계 n이 고정되어 있고, f에 대한 추가적인 가정 없이는 위의 근사치의 오차에 대해 거의 말할 수 없다: 심하게 진동하는 함수의 경우 리만 합이 임의로 리만 적분으로부터 멀어질 수 있다는 것은 분명하다.
아이덴티티
아래의 공식은 유한합계를 포함한다; 삼각함수나 다른 초월함수와 관련된 표현의 무한합 또는 유한합은 수학 급수 목록을 참조한다.
일반 아이덴티티
- n= t ( n )= n = t f( n ) { \{ n=\ f ( ) \ \ _ { n}f ( ) \cdot f ( n ) \ cdot } f ( [3]n )
- n= f (n )± ∑ = ( n) ( ( )± ( display \{ n= t ( \} g ( = s n } f ( ) \ pm } ( n )
- ∑ = f( n ) ∑ + +p f( -p ) { \{ n=s ( n ) \{ n= s + p f ( n - p )\ _ t + } f ( n - p )
- 유한 집합 A에서 집합 로의 바이젝션 θ에 대한 nB ( n) m A ( n ) \{ n \ f ( \ ( m ) 、 \ sum f ( \ sigma ) 、 \ sigma } } f ( \ sum } f ( n )} f ( \ in A )、 \ 、 \ sigm 、 \ } f ( \ sigm } f ( \ sigma } f ( \ sigma
- n= t ( n ) (n ) +∑ + (n ) { \ n=s ( n ) \{ n=s } f ( n ) + \ { s}f ( n ) + { n \ sum _ { j + t f ( n ) ( n ) f ( n ) ( n ) ( n ) sum ) sum )
- n= (n )=∑ n= b (n ) -∑ = - (n ){ \ { n=ab ( n ) f ( n ) \{ n= ( n ) ( n ) - \ sumb ( n ) f ( n ) - ( 。
- n= t ( n ) ∑ = t - f( -n ){ display \_ =}{} (첫 번째 항에서 마지막까지의 합은 마지막 항까지의 합과 첫 번째 항까지의 합과 같다
- n= f (n ) ∑ = ( -n ){ \n=} (위 공식의 특정 경우
- i= k 1 j= , j 1、 = , \{ i = _ { 0 } { _ {} \ { jl _ { 0 } = { l _ { l _ { n 1} = { } _ { l _ i }
- }(환산성과 연관성의 다른 응용 프로그램)
- = s + f( n ) n= (n ) +∑ = t ( +1 ) ( \{ n= 2 s +f ( n ) \_ {=s + f ( n + 1f ( n )
- = + 2 ( n ) s + ( ) + n s + 1t ( -1 ){ \ sum { n = 1 f ( n ) f ( n_ { n + f ( n +) _
- ) ( = j ) 0 j b \ \ \ left ( \ { i= 0 }^{ } _ { } \ ) \ ( \ _ }^{ right ) _ n 0 .
- = s m= c j (∑ = m i ) (display =t j ) ( j = t j ) { \{ = { { i } { _ { j } = \_ (((((( ( ( ( ( )
- n= log b ( n ) b n t f ( n ) \{ n= \ _ { } \_ { b } \ log _ { n{ } f ( )\ log _ { n } f ( n )\log _ n )\ log _ t (곱)\ log f (곱셈의 로그 인수의 합)
- n t ( ) n t ( C _)}C} (지수의 합은 지수의 곱이다.)
산술 급수의 거듭제곱과 로그
- i에 의존하지 않는 모든 c에 대해 i= c = c { \{ i=1} = \ exc}
- i= ni i= n ( + 1 )_ i=1)}{2 \} (자연수로 [2]: 52 이루어진 가장 간단한 산술 수열의 합계
- i= n ( - 1) 2 ( \ \ { i=1} ( } 첫 번째 홀수 자연수의 합계)
- i= i ( +1 ){ \1)\} (첫 번째 짝수 자연수의 합계
- i= log i=log ! { \i=1}\ i n!\qquad} (대수의 합은 곱의 로그
- 6}}\}(첫 번째 정사각형의 합, 정사각형의 숫자를 참조).[2]: 52
- )^{2}}{4}}{2}(니코마치 정리)
보다 일반적으로 p>에 Faulhaber 공식(\ p)이 있습니다.
서 B k})는 베르누이 수를 나타내고 ( k {는 이항 계수입니다.
지수 단위의 합계 지수
다음 합계에서는 a가 1과 다른 것으로 가정한다.
- i= - - n 1- a - a 1 - a \ \}^{ a^{i} = n}} { (기하 급수의 합
- i= - 1 2 i - - 1 { \{ 0 }^{ n - 1 }{\{ }= - { \ { 2 ^ { - 1 }} = 2 - { 2 = 1 / 2)
- i= - - a +( - ) + 1 (- ) 2 ( \ 0}^{ia^{i}=}}{n-1a}}}}}{n-a}}}}}}}}}}}}}}}{n__________1-a__________
-
- (산술-수열 합계)
이항 계수 및 인자
이항 계수와 관련된 매우 많은 합계 식별성이 존재합니다(구체 수학의 전체 장은 기본 기술에만 전념합니다).가장 기본적인 것 중 몇 가지는 다음과 같습니다.
이항 정리 포함
- i= ( ) - b ( a+ b) , { \ a^{b^{in}, 이항 정리
- i= ( ni )=n , { \{ i= 0 \}} 한 경우a = b = 1
- i= n ( i ) i( - ) - i \ \ { i= 0n \ choose i } p^{ i }(1 p = a = 1 - b ( ≤ 0 0 0 , {\ 1 ) n、 \ sum _ 1 \ i \ q {\ 1 \ 1 \ 、 \ 0 1 \ q 1 \ , 1 \ sum _ q 1 \q 1 \ q 1 q 1 \
- i= (n i ) ( -1) , { \ \2^{ = b = a에 대한 도함수 값
- i= n ( i) + 1= n+ - n+ , \ \+1 a = b+1의 이항식 a에 대한 값
치환 번호 포함
- n i _}=\ n en\{Z 여기서 x { \는 바닥 함수를 나타냅니다.
다른이들
조화수
증가율
- -1보다 큰 실수 c에 대해 i= n ∈( + 1) { _ i ( 1})
- i= n i∈( ( log ) {_ { \_{n)\in \Theta(\ (\log _{e}n) 참조
- i= ∈( (n ) { \i=1 c \ (c})
- 음이 아닌 실수 c의 경우 = n ( ) c ∈ c \ \ }^{ \( n \ (c}} }
- i= n ( ) c⋅ + 1⋅( ) c \)^{ \ ( )
- i= n ( ) c⋅ d⋅ i∈ 、 ⋅ ( ) n\ \{ i=1 }^{ n ( )^{
역사
- 1675년, 고트프리드 빌헬름 라이프니츠는 헨리 올덴부르크에게 보낸 편지에서, 미분(라틴어: 미적분 수마토리우스)의 합을 표시하기 위해 기호 the를 제안했고, 따라서 [4][5][6]S자 모양을 만들었다.이 기호의 이름은 나중에 요한 베르누이와의 [6]교환에서 비롯되었다.
- 1755년, 합계 기호 δ는 Leonhard Oiler의 Institutiones calci differentialis에서 [7][8]증명되었다.오일러는 다음과 같은 식에서 기호를 사용합니다.
- 1772년에 Lagrange는 [7][9]σ과 is의n 사용을 증명했다.
- 1823년에는 대문자 S가 급수의 합계 기호로서 증명된다.이 사용법은 분명히 [7]널리 퍼져 있었다.
- 1829년에 푸리에와 C. G. J. 자코비가 가산 기호 [7]δ를 증명했다.푸리에에는 다음과 같은 하한 및 상한이 사용됩니다.[10][11]
「 」를 참조해 주세요.
- 대문자 pi 표기법
- 아인슈타인 표기법
- Iverson 브래킷
- 반복 이진 연산
- 카한 가산 알고리즘
- 제품(수학)
- 부품별 합계
- ∙ 단일 글리프 (U+2211 N-ARY SUMMATION)
- ∙ 페어링된 글리프의 시작(U+23B2 SUMMATION TOP)
- ∙ 페어링된 글리프의 끝부분(U+23B3 SUMTION Bottom)
메모들
- ^ 자세한 내용은 삼각형 번호를 참조하십시오.
- ^ 합계 표기법 및 합계 산술에 대한 자세한 설명은 를 참조하십시오.Graham, Ronald L.; Knuth, Donald E.; Patashnik, Oren (1994). "Chapter 2: Sums". Concrete Mathematics: A Foundation for Computer Science (PDF) (2nd ed.). Addison-Wesley Professional. ISBN 978-0201558029.[영구 데드링크]
- ^ 의 와 혼동할 가능성이 없는 상황에서
- ^ 더미 변수의 이름은 (정의상) 상관없지만 혼동의 위험이 있는 경우 정수를 나타내기 위해 보통 알파벳 중간 문자( i ~q를 사용합니다.예를 들어, 이 해석에 의심의 여지가 없다고 해도, 많은 수학자들이 k k가 x x를 k(\ k와 된 위의 공식에서 보는 은 약간 혼란스러워 보일 수 있습니다. 수학 공식의 표기법도 참조하십시오.
레퍼런스
- ^ "Summation Notation". www.columbia.edu. Retrieved 2020-08-16.
- ^ a b c d 이산 및 조합 수학 핸드북, Kenneth H. Rosen, John G.마이클스, CRC 프레스, 1999, ISBN 0-8493-0149-1.
- ^ a b "Calculus I - Summation Notation". tutorial.math.lamar.edu. Retrieved 2020-08-16.
- ^ Burton, David M. (2011). The History of Mathematics: An Introduction (7th ed.). McGraw-Hill. p. 414. ISBN 978-0-07-338315-6.
- ^ Leibniz, Gottfried Wilhelm (1899). Gerhardt, Karl Immanuel (ed.). Der Briefwechsel von Gottfried Wilhelm Leibniz mit Mathematikern. Erster Band. Berlin: Mayer & Müller. p. 154.
- ^ a b 카조리(1929), 페이지 181-182.
- ^ a b c d 카조리(1929년), 페이지 61
- ^ Euler, Leonhard (1755). Institutiones Calculi differentialis (in Latin). Petropolis. p. 27.
- ^ Lagrange, Joseph-Louis (1867–1892). Oeuvres de Lagrange. Tome 3 (in French). Paris. p. 451.
- ^ Mémoires de l'Académie royale des sciences de l'Institut de France pour l'année 1825, tome VIII (in French). Paris: Didot. 1829. pp. 581-622.
- ^ Fourier, Jean-Baptiste Joseph (1888–1890). Oeuvres de Fourier. Tome 2 (in French). Paris: Gauthier-Villars. p. 149.
참고 문헌
- Cajori, Florian (1929). A History Of Mathematical Notations Volume II. Open Court Publishing. ISBN 978-0-486-67766-8.
외부 링크
 Wikimedia Commons에서의 요약 관련 매체
Wikimedia Commons에서의 요약 관련 매체










![{\displaystyle \scriptstyle {\sqrt[{\text{degree}}]{\scriptstyle {\text{radicand}}}}\,=\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5582d567e7e7fbcdb728291770905e09beb0ea18)






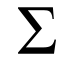




 대한 f
대한 f
 대체 표기법입니다.유사하게,
대체 표기법입니다.유사하게,










 합계에 항이 하나뿐이고,
합계에 항이 하나뿐이고, 


![\sum _{k{\mathop {=}}a}^{b}f(k)=\int _{[a,b]}f\,d\mu](https://wikimedia.org/api/rest_v1/media/math/render/svg/3df03fc79c21c319ce553adbbd688204560d2f47)

![[a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)














































 이항식
이항식 























