대체모형

생물학에서 DNA 시퀀스 진화의 모델이라고도 불리는 대체 모델은 진화 시간에 따른 변화를 설명하는 마르코프 모델이다.이들 모델은 기호의 순서(DNA의 경우 A, C, G, T)로 대표되는 고분자의 진화적 변화(예: DNA 시퀀스)를 설명한다.치환 모델은 다중 시퀀스 정렬 데이터를 사용하여 계통 생성 트리의 가능성을 계산하는 데 사용된다.따라서 치환 모델은 치핵생식에 대한 베이지안 추론뿐만 아니라 치핵생식에 대한 최대우도 추정의 중심이다.진화 거리 추정치(공통 조상으로부터 분리된 한 쌍의 시퀀스 이후 발생한 대체물의 수)는 대체 모델을 사용하여 일반적으로 계산된다(진화 거리는 이웃 결합과 같은 거리 방법에 대한 입력으로 사용된다.대체 모델은 또한 계통 위상이 주어진 현장 패턴 빈도의 빈도를 예측하는 데 사용될 수 있기 때문에 계통발생적 불변성의 중심이다.대체 모델은 특정 나무와 관련된 유기체 그룹에 대한 시퀀스 데이터를 시뮬레이션하기 위해 필요하다.

Phylogenetic tree 토폴로지

계통생성 트리 위상은 종종 관심의 매개 변수다.^[1] 따라서 가지 길이와 대체 과정을 설명하는 다른 매개 변수는 종종 성가신 매개 변수로 간주된다.그러나 생물학자들은 때때로 모델의 다른 측면에 관심을 가진다.예를 들어 가지 길이, 특히 나뭇가지 길이가 화석 기록의 정보 및 진화의 기간을 추정하는 모델과 결합되는 경우.^[2]진화 과정의 다양한 측면에 대한 통찰력을 얻기 위해 다른 모델 매개변수가 사용되어 왔다.K_a/K_s 비율(코돈 대체 모델에서는 Ω이라고도 함)은 많은 연구에서 관심 있는 매개 변수다.K_a/K_s 비율은 단백질 코딩 부위에서 자연선택의 작용을 검사하는데 사용될 수 있다;^[3] 그것은 아미노산(비동기 대체)을 인코딩된 아미노산(동명 대체)을 변경하지 않는 것과 바꾸는 뉴클레오티드 대체물의 상대 비율에 대한 정보를 제공한다.

데이터 시퀀싱에 응용 프로그램

대체 모델에 대한 대부분의 작업은 DNA/RNA와 단백질 시퀀스 진화에 초점을 맞춰왔다.알파벳이 네 개의 뉴클레오티드(A, C, G, T)에 해당하는 DNA 시퀀스 진화의 모델은 아마도 이해하기 가장 쉬운 모델일 것이다.DNA 모델은 RNA 바이러스 진화를 검사하는데도 사용될 수 있다; 이것은 RNA가 또한 4개의 뉴클레오티드 알파벳 (A, C, G, U)을 가지고 있다는 사실을 반영한다.그러나 치환 모델은 모든 크기의 알파벳에 사용될 수 있다; 알파벳은 단백질을 위한 20개의 단백질 발생 아미노산과 정렬된 단백질 코딩 유전자 배열의 감지 코돈(즉, 표준 유전자 코드에 아미노산을 인코딩하는 61개의 코돈)이다.실제로 대체 모델은 특정 알파벳을 사용하여 인코딩할 수 있는 모든 생물학적 문자(예: 3차원 단백질 구조에서 아미노산의 순응에^[4] 대한 정보와 결합한 아미노산 시퀀스)에 대해 개발될 수 있다.

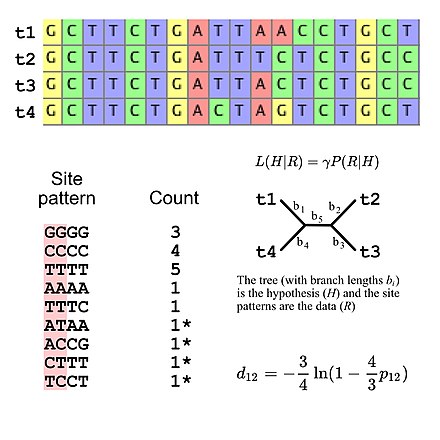
진화 연구에 사용되는 대부분의 대체 모델은 현장 간의 독립성을 가정한다(즉, 현장 패턴이 시퀀스 정렬에 있는 위치에 관계없이 특정 현장 패턴을 관찰할 확률은 동일하다).이것은 선형에 나타나는 모든 현장 패턴의 확률을 계산하고 그 값을 사용하여 선형의 전체 우도를 계산하면 되기 때문에 우도 계산을 단순화한다(예: DNA 시퀀스 진화의 일부 모델이 주어진 3개의 "GGGGG" 현장 패턴의 확률은 단순히 a의 확률이다).단일 "GGGG" 사이트 패턴이 세 번째 전력으로 상승).즉, 대체 모델은 부지 패턴 주파수에 대한 특정 다항 분포를 암시하는 것으로 볼 수 있다.4개의 DNA 시퀀스에 대한 다중 시퀀스 정렬을 고려할 경우 256개의 가능한 사이트 패턴이 있으므로 사이트 패턴 빈도에 대해 255도의 자유도가 있다.만약 DNAevolution,[5]는 한 주파수만 나무 형태와 가지 길이가 예상 사이트 패턴을 계산할 수 있는 단순한 대체 모델은 Jukes-Cantor 모델을 이용하여(4taxa 사회적 기반이 없는 bifurcating 나무 제공 하지만 추세가 예상되는 사이트 패턴~주파수를 자유의 5도를 사용하여 지정할 수 있습니다.e5가지 분지 길이를 가지다.

대체 모델은 또한 몬테카를로 방법을 사용하여 시퀀스 데이터를 시뮬레이션할 수 있게 한다.시뮬레이션된 다중 시퀀스 정렬은 분자 진화와 분자 계통 유전학 분야에서 특정 통계적 시험에^[6] 대한 null 분포를 생성하는 데 사용될 수 있다.이러한 테스트의 예로는 트리 토폴로지를 검사하는 데 사용할 수 있는 모델 적합성^[7] 테스트와 "SOWH 테스트"가 있다.^[8][9]

형태학적 데이터에 대한 적용

대체 모델을 사용하여 생물학적 알파벳을 분석할 수 있다는 사실은 표현형 데이터 집합^[10](예: 형태학적 및 행동적 특성)에 대한 진화 모델을 개발할 수 있게 했다.일반적으로 "0"은 특성이 없음을 나타낼 때 사용되며 "1"은 복수의 상태를 이용하여 문자를 채점할 수도 있지만 특성이 있음을 나타낼 때 사용된다.이 프레임워크를 사용하여 적절한 모드를 사용하여 분석하기 전에 일련의 표현형들을 이진 문자열로 인코딩할 수 있다.이것은 "토이"의 예를 사용하여 설명될 수 있다: 우리는 이진 알파벳을 사용하여 "깃털", "레이즈 알", "모피", "온혈성", "동력 비행 가능" 등의 표현형질을 평가할 수 있다.이 장난감 예에서 벌새는 순서 11011(대부분의 다른 새들은 같은 줄을 가지고 있을 것이고, 타조는 순서 11010, 소는 (그리고 대부분의 다른 육지 포유류는) 00110, 박쥐는 00111을 가질 것이다.계통생성 트리의 가능성은 이러한 이항 시퀀스와 적절한 대체 모델을 사용하여 계산할 수 있다.이러한 형태론적 모델의 존재는 형태론적 데이터만을^[11] 사용하거나 형태론적 데이터와 분자적 데이터의^[12] 조합(화석세자의 누락 데이터로 채점됨)을 이용하여 화석세금으로 데이터 행렬을 분석할 수 있게 한다.

피복물학 분야에서 분자 또는 표현형 데이터의 사용과 대체 모델을 이용한 형태학적 문자 분석 사이에는 분명한 유사성이 있다.그러나 시스템 커뮤니티에서는 '모델 없는 분석'으로 봐야 하는지에 대한 문제를 놓고 떠들썩한 논쟁이^[a] 벌어졌다.클래지스틱스 분야(가장 엄격한 의미에서 정의됨)는 계통생리학적 추론에 대한 최대 편협성 기준의 사용을 선호한다.^[13]많은 외피스트들은 최대 파시모니가 대체모델에 근거한다는 입장을 거부하며 (많은 경우) 칼 포퍼의 철학을 이용한 파시모니의 사용을 정당화한다.^[14]그러나 "파시모니와 동등한" 모델^[15](즉, 분석에 사용될 때 최대 파시모니 트리를 산출하는 대체 모델)이 존재하면 파시모니를 대체 모델로 볼 수 있다.^[1]

분자 시계와 시간 단위

일반적으로 계통생식수(Phylogenetic tree)의 가지 길이는 사이트당 예상 대체수로 표현된다. 진화모델이 조상순서의 각 사이트가 특정 자손순서로 진화할 때까지 전형적으로 x 대체를 경험하게 된다는 것을 나타내는 경우, 조상 및 자손은 다음과 같이 간주된다.가지 길이 x로 구분하여

때때로 나뭇가지 길이는 지질학적 연도로 측정된다.예를 들어, 화석 기록은 조상 종과 후손 종 사이의 연수를 결정하는 것을 가능하게 할 수 있다.어떤 종들은 다른 종들보다 빠른 속도로 진화하기 때문에, 가지 길이의 이 두 척도가 항상 직접적인 비례는 아니다.연간 사이트당 예상 대체 횟수는 그리스 문자 mu(μ)로 표시되는 경우가 많다.

모델은 어떤 종의 진화를 조사하든 연간 μ당 예상 대체 횟수가 일정하다면 엄격한 분자시계를 가지고 있다고 한다.엄격한 분자시계의 중요한 함축은 조상의 종과 현재의 후손들 사이에서 예상되는 대체의 수는 어떤 후손 종을 검사하는 것과 무관해야 한다는 것이다.

분자 시계가 엄격하다는 가정은 특히 오랜 진화 기간 동안 비현실적인 경우가 많다는 점에 유의하십시오.예를 들어, 설치류는 영장류와 유전적으로 매우 유사하지만, 게놈의 일부 영역에서 분리한 이후 추정된 시간 동안 훨씬 더 많은 대체물을 경험했다.^[16]이것은 그들의 짧은 생성 시간,^[17] 더 높은 신진대사율, 인구 구조 증가, 분화율 증가, 또는 더 작은 신체 크기 때문일 수 있다.^[18][19]분자 시계 가정 하에서 캄브리아기 폭발과 같은 고대 사건을 연구할 때, 클래디스트 데이터와 계통생성 데이터 사이의 빈약한 동시성이 종종 관찰된다.다양한 진화 속도를 허용하는 모델에 대한 연구가 있었다.^[20][21]

계통생성 내 서로 다른 진화 라인 사이에서 분자 시계의 비율의 변동성을 고려할 수 있는 모델을 "강성"에 반대하여 "완화"라고 부른다.그러한 모델에서는 비율이 조상들과 후손들 사이에 상관관계가 있거나 없는 것으로 가정할 수 있으며, 라인업들 간의 비율 변동은 많은 분포에서 도출될 수 있지만 대개 지수 분포와 대수 정규 분포가 적용된다.계통생식을 적어도 두 칸(직렬의 집합)으로 나누고 각각에 엄격한 분자시계를 적용하지만 비율이 다른 특별한 경우를 '국소외분자시계(local molecular clock, lineages set)가 있다.

시간 경과 및 정지 모델

많은 유용한 대체 모델은 시간을 되돌릴 수 있다. 수학의 관점에서 모델은 다른 모든 매개변수(예: 두 시퀀스 사이에 예상되는 사이트당 대체 횟수)가 일정하게 유지되는 한 어떤 시퀀스가 조상이고 어떤 하위 시퀀스인지는 상관하지 않는다.

실제 생물학적 데이터의 분석을 수행할 때, 일반적으로 현재 종에 대해서만 조상 종의 서열에 접근할 수 없다.그러나 모델이 시간을 되돌릴 수 있을 때, 어떤 종이 조상의 종이었는지는 상관이 없다.대신 계통생식 나무는 어느 종을 사용해도 뿌리를 내릴 수 있고, 나중에 새로운 지식을 바탕으로 다시 뿌리를 내리거나 뿌리째 뽑지 않은 채 방치할 수 있다.왜냐하면 '특별한' 종은 없기 때문인데, 결국 모든 종은 같은 확률로 서로에게서 파생될 것이다.

모델은 특성을 만족하는 경우에만 시간을 되돌릴 수 있다(아래에 표기법이 설명됨).

${\displaystyle \pi _{i}Q_{ij}=\pi _{j}Q_{ji}}}}$

또는 동등하게, 상세 잔액 속성,

${\displaystyle \pi _{i}P(t)_{ij}=\pi _{j}P(t)_{ji}}}}$

모든 i, j, t에 대해.

시간 경과성을 역학성과 혼동해서는 안 된다.Q가 시간에 따라 변하지 않으면 모델은 정지해 있다.아래의 분석은 고정 모델을 가정한다.

대체 모델의 수학

고정, 중립, 독립, 유한 현장 모델(진화의 일정한 비율을 가정)에는 염기(또는 문자) 주파수의 평형 벡터인 π과 한 유형의 염기들이 다른 유형의 염기들로 변하는 비율을 설명하는 비율 매트릭스 Q가 있다. i parametersj에 대한 요소 ${\displaystyle {Qi}_{}}$ ${\displaystyle j_{}}$ ${\$는 다음과 같다.베이스 J에 어느 베이스로 가는지 평가하다.Q 행렬의 대각선은 행의 합이 0이 되도록 선택된다.

${\displaystyle Q_{i}=-{\sum _{\lbrace j\mid j\neq i\rbrace }Q_{ij}}\...}$

평형 열 벡터 π은 속도 매트릭스 Q:에 의해 소멸되어야 한다.

${\displaystyle \pi \,Q=0\,.}$

전환 행렬 함수는 가지 길이(일부 시간 단위, 대체 가능한 경우)에서 조건부 확률 행렬까지의 함수다.$P{\displaystyle }$( ${\displaystyle t}$) ${\displaystyle P(t)}$로 표시된다$.$i^th 열과 ${\displaystyle \mathrm{j^th}}$ 행의 $항목$인 P ${\displaystyle i_{}}$ ${\displaystyle j_{}}$( t${\displaystyle }$) ${\displaystyle P_{ij}(t$는 시간 t 후에 주어진 위치에 base j가 있을 확률로, 0시에 그 위치에 base i가 있을 것을 조건으로 한다.모델이 시간을 되돌릴 수 있는 경우, 한 시퀀스가 다른 시퀀스의 조상이 아니더라도 두 시퀀스 사이의 총 분지 길이를 알면 두 시퀀스 간에 이 작업을 수행할 수 있다.

P_ij(t)의 점증적 특성은 P_ij(0) = Δ이며_ij 여기서 Δ는_ij Kronecker 델타 함수다.즉, 수열과 그 자체 사이에는 염기 구성의 변화가 없다.At the other extreme, ${\displaystyle \lim _{t\rightarrow \infty }P_{ij}(t)=\pi _{j}\,,}$ or, in other words, as time goes to infinity the probability of finding base j at a position given there was a base i at that position originally goes to the equilibrium probability that there is base j at that 위치(원래 베이스와 무관하게)더욱이, 모든 t에 대해$$ ${\displaystyle p}$ P${\displaystyle }$(${\displaystyle t}$) = ${\displaystyle \pi }$ ${\displaystyle \pi$P($t)=\pi$}을 따른다.

전환 매트릭스는 매트릭스 지수를 통해 속도 매트릭스에서 계산할 수 있다.

${\displaystyle P(t)=e^{Qt}=\sum _{n=0}^{\n^{n}{\frac{t^{n}}{n!}}\,,}$

여기서 Q는ⁿ 매트릭스 Q에 n의^th 힘을 부여하기에 충분한 횟수를 곱한 것이다.

Q가 대각선이 가능한 경우 매트릭스 지수 값을 직접 계산할 수⁻¹ 있다: Q = U of U를 Q의 대각화(대각화)로 한다.

${\displaystyle \lambda ={\begin{pmatrix}\lambda _{1}\ldots &0&\ldots &\lambda _{4}\end{pmatrix}\...}}$

여기서 λ은 대각 행렬이며$,{\displaystyle }$ 여기서 { ${\displaystyle {\lambda }_{}}$ i${\displaystyle {}_{}}$ ${\displaystyle \lbrace \lbrace$ \$lambda$_{i}\rbrace $}}$은 Q의 고유값이며, 각각 그 다중성에 따라 반복된다.그러면

${\displaystyle P(t)=e^{Qt}=e^{U^{-1}(\Lambda t)U}=U^{-1}e^{\Lambda t}\,U\...}$

대각 행렬 e가^Λt 주어지는 위치

${\displaystyle e^{\lambda t}={\begin{pmatrix}e^{\lambda _{1}t}&\ldots &0&\ldots &e^{4}lambda _{4}t}\end{pmatrix\},},\,},\,\,\,\,\,\,},},}}$

일반화 시간 되돌리기 가능

GTR(Generalized time roversible)은 가능한 가장 일반적인 중립적이고 독립적이며 유한한 시간역전 모델이다.1986년 사이먼 타바레(Simon Tavaré)에 의해 일반 형식으로 처음 서술되었다.^[22]GTR 모델은 흔히 출판물에서 일반 시간 되돌릴 수 있는 모델이라고 불리며,^[23] REV 모델이라고도 불린다.^[24]

뉴클레오티드에 대한 GTR 파라미터는 평형 베이스 주파수 벡터${\displaystyle \stackrel{}{}}\pi {\displaystyle \stackrel{}{}}$→ = (${\displaystyle {1\mathrm{}}_{}}$ 1${\displaystyle {}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$2, ${\displaystyle {}_{}{3\mathrm{}}_{}}$ , ${\displaystyle {4\mathrm{}}_{}}$ 4$){\displaystyle {\vec{\pi }}}}=(\pi _{1},\pi _{2},\pi {}}, 속도 매트릭스$로 구성된다$.$

${\displaystyle Q={\begin{pmatrix}{-(x_{1}+x_{2}+x_{3})}&, x_{1}&, x_{2}&, x_{3}\\{\pi_{1}x_{1}\over \pi _{2}}&{-({\pi_{1}x_{1}\over \pi_{2}}+x_{4}+x_{5})}&, x_{4}&, x_{5}\\{\pi_{1}x_{2}\over \pi _{3}}&{\pi_{2}x_{4}\over \pi _{3}}&{-({\pi_{1}x_{2}\over \pi_{3}}와{\pi_{2}x_{4}\over \pi_{3}}+x_{6})}&, x_{6}\\{\pi. _{1}x_{3}\over \pi _{4}}&{\pi_{2}x._{5} \over \pi _{4}}&{\pi _{3}x_{6} \over \pi _{4}}&{-({\pi _{1}x_{3} \over \pi _{4}}+{\pi _{2}x_{5} \over \pi _{4}}+{\pi _{3}x_{6} \over \pi _{4}})}\end{pmatrix}}}$

모델은 시간을 되돌릴 수 있어야 하고 긴 시간 동안 평형 뉴클레오티드(기본) 주파수에 접근해야 하기 때문에 대각선 아래의 각 속도는 대각선 위의 호혜율에 두 베이스의 평형비를 곱한 것과 같다.이와 같이 뉴클레오티드 GTR은 6개의 치환율 파라미터와 4개의 평형 베이스 주파수 파라미터를 필요로 한다.4개의 주파수 파라미터는 1로 합해야 하기 때문에 자유 주파수 파라미터는 3개뿐입니다.총 9개의 자유 매개변수는 종종 8개의 매개변수에 단위 시간당 전체 대체 횟수인$$$\mu {\displaystyle }$({\$displaystyle \mu })$를 더하여 감소한다.대체물에서 시간을 측정할 때(${\displaystyle }$ ${\displaystyle \mu }$=1) 8개의 자유 매개변수만 남게 된다.

일반적으로 파라미터 수를 계산하려면 매트릭스에서 대각선 위의 항목 수를 계산한다. 즉 사이트 ${\displaystyle \frac{{n\mathrm{}}^{}}{}}$ 2${\displaystyle \frac{{}^{}}{}}$- ${\displaystyle \frac{\mathrm{}}{}}$ 2 ${\$\$2}$ \{$n{\displaystyle }$} \}{n} $\}{$$n$}} \$displaystyle \mu$$}}}$ 사이트당 특성 값 n을 계산한 다음 평형 주파수에 대해 n-1을 추가하고 1을 뺀다.알겠지

${\displaystyle {{n^{2}-n} \over 2}+(n-1)-1={1 \over 2}n^{2}+{1 \over 2n-2}}$

예를 들어, 아미노산 염기서열(단백질을 구성하는 20개의 "표준" 아미노산이 있다)의 경우 208개의 매개변수가 있음을 발견할 수 있을 것이다.그러나 게놈의 코딩 영역을 연구할 때는 코돈 대체 모델(코돈은 단백질 내 아미노산 1개에 대해 3개의 베이스와 코드)으로 작업하는 것이 더 일반적이다.4 3$$ = ${\displaystyle {64\mathrm{}}^{}}$ ${\displaystyle 4^{3}=64}$ 코돈이 있어 2078개의 자유 매개변수가 발생한다.$단$, 둘 이상의 베이스가 다른 코돈 간 전환 속도는 0으로 가정하는 경우가 많아 무료 파라미터의 개수가 ${\displaystyle \frac{20}{}}$× ${\displaystyle \frac{19}{}}$× ${\displaystyle \frac{\mathrm{}}{}}$ +${\displaystyle }$3 ${\displaystyle 2}$+ ${\displaystyle 63}$- 1 = ${\displaystyle 632}${\$displaystyle$19\$time$ 3$} \{20$\time 3} $\{}}{}}}}+63-1=632}$ 매개$$ $변수$를 초과하여 감소시킨다.또 다른 일반적인 관행은 중지(또는 말도 안 되는) 코돈을 금지함으로써 코돈의 수를 줄이는 것이다.이는 생물학적으로 타당한 가정이다. 왜냐하면 정지 코돈을 포함하면, 조상 $코돈$이 i ${\displaystyle i}$인 경우$$, $지각{\displaystyle }$ $코돈{\displaystyle }$ j ${\displaystyle t}$ 이후에$$ 감지 코돈 j {\displaysty t$}$을 찾을 확률을 계산하고 있다는 것을 의미하기 때문이다.숙성한 코돈

뉴클레오티드 GTR 모델에 대한 즉각적인 속도 행렬(${\displaystyle }$ ${\displaystyle Q$} 행렬$$)을 작성하는 대안(일반적으로 사용되는^{[23][25][26][27]}) 방법은 다음과 같다.

${\displaystyle Q={\begin{pmatrix}{-(a\pi_{C}+b\pi_{G}+c\pi_{T})}&, a\pi _{C}&, b\pi _{G}&,c\pi _{T}\\a\pi _{A}&,{-(a\pi_{A}+d\pi_{G}+e\pi_{T})}&, d\pi _{G}&,e\pi _{T}\\b\pi _{A}&, d\pi _{C}&,{-(b\pi_{A}+d\pi_{C}+f\pi_{T})}&,f\pi _{T}\\c\pi _{A}&, e\pi _{C}&, f\pi _{G}&,{-(c\pi_{A}+e\pi_{C}+f\pi_{G})}\end{시.atrix}}}$

$Q{\displaystyle }$ ${\displaystyle Q}$ 행렬이$$ 정규화되므로 -${\displaystyle \underset{}{\overset{}{}}}$ ${\displaystyle \underset{}{\overset{}{k}}}$= 1 ${\displaystyle \underset{}{\overset{}{\mathrm{}}}}$ ${\displaystyle \underset{}{\overset{}{}}{}_{}}$ i ${\displaystyle Q_{}}$ ${\displaystyle {}_{}{}_{}}$= ${\displaystyle 1}$ ${\displaystyle -\sum _{k=1}^{4}\pi _{i}Q_{i}=1$}는 정규화된다$.$

${\displaystyle {이}_{}}$ 표기법은 모든 모델 매개변수가 "교환성" 매개변수$({\displaystyle a$$}$ ~ ${\displaystyle }$ ${\$$displaystyle$ $f$$\})$에 해당하기 때문에 Tavaré가 원래 사용한 표기법보다 이해하기 쉽다.encies${\displaystyle \stackrel{}{}}\pi {\displaystyle \stackrel{}{}}$ →${\displaystyle }$= ($\pi {\displaystyle }$ ${\displaystyle A_{}}$, ${\displaystyle {}_{}}$ ${\displaystyle C_{}}$ ,${\displaystyle {}_{}{}_{}}$ G ,${\displaystyle {}_{}{\pi }_{}}$ T${\displaystyle {}_{}}$) ${\displaystyle {\vec{\pi }}=(\pi _{A},\pi$ $_$${G},\T$}). Q ${\$$displaysty$ Q$}$ 행렬의$$ 뉴클레오티드가 알파벳 순서로 작성되었다는 점에 유의한다$.$즉, 위의 $Q{\displaystyle }$ ${\displaystyle Q}$ 행렬에$$ 대한 전환 확률 행렬은 다음과 같을 것이다.

${\displaystyle P(t)=e^{Qt}={\begin{pmatrix}p_{\mathrm{AA}}(t)&, p_{\mathrm{AC}}(t)&, p_{\mathrm{AG}}(t)&, p_{\mathrm{AT}}(t)\\p_{\mathrm{CA}}(t)&, p_{\mathrm{CC}}(t)&, p_{\mathrm{CG}}(t)&, p_{\mathrm{CT}}(t)\\p_{\mathrm{GA}}(t)&, p_{\mathrm{GC}}(t)&, p_{\mathrm{GG}}(t)&, p_{\mathrm{GT}}(t)\\p_{\mathrm{TA}. }(t)&, p_{\mathrm{TC}}(t)&, p_{\mathrm{TG} }(t)&p_{\mathrm {TT} }(t)\end{pmatrix}}$

어떤 출판물은 뉴클레오티드를 다른 순서로 쓴다(예를 들어, 어떤 저자들은 두 개의 청주와 두 개의 피리미딘을 함께 그룹화하기로 선택한다; DNA 진화의 모델도 참조한다).이러한 표기법 차이 $때문$에 Q$${\$displaystyle Q$} 행렬을$$ 작성할 때 주의 순서에 대해 명확히 하는 것이 중요하다.

$이{\displaystyle }$ 표기법의 값은 뉴클레오티드 i ${\displaystyle i}$에서 뉴클레오티드 j ${\$$displaystyle j}$ {\$displaystyle r_{ij}\pi _{j$로 즉시 변경될 수 있다는$$ 것이다. 여기서 ${\displaystyle {\mathrm{ri}}_{}}$ ${\displaystyle j_{}}$ ${\$은 뉴클레오티드의 교환성 $i}$및 {\$displaystytytytytimestytimestytimestym$ i}이다.${\displaystyle j}$$$ ${\displaystyle j}$과(와) $\$ j {\$displaystyle$ \$pi$_{$j}$는 j ${\displaystyle t^{}}$h {\$displaysty$j^{$th}}$ 뉴클레오티드의$$ 평형 주파수다.위에 표시된 행렬은 판독성을 위해 교환성 매개변수에 $대해{\displaystyle }$$$ ${\displaystyle a}$ ~ $f$ ${\displaystyle f}$ 문자를 사용하지만, 이러한 매개변수는 $r{\displaystyle {}_{}}$ ${\displaystyle i_{}}$ ${\displaystyle j_{}}$ ${\$ 표기법$$($예{\displaystyle }$: a${\displaystyle }$= ${\displaystyle R_{}}$ ${\displaystyle C_{}}$ ${\$을 사용하여 체계적으로 작성할 수도 있다.$AC$ b${\displaystyle }$= ${\displaystyle {}_{}}$ ${\displaystyle A_{}}$ ${\displaystyle G_{}}$ ${\$$AG}$등).

교환성 매개변수에 대한 뉴클레오티드 첨자의 순서는 무관하다는 점에 유의하십시오(예: $r{\displaystyle {}_{}}$ ${\displaystyle A_{}}$= r ${\displaystyle {}_{}}$ ${\displaystyle A_{}}$ ${\$$AC}=r_{CA}}$) but the transition probability matrix values are not (i.e., ${\displaystyle p_{\mathrm {AC} }(t)}$ is the probability of observing A in sequence 1 and C in sequence 2 when the evolutionary distance between those sequences is ${\displaystyle t}$ whereas ${\displaystyle p_{\math$$rm {CA} }(t)}$은 동일한 진화 거리에서 순서 1에서 C를, 순서 2에서 A를 관측할 확률이다$$.

임의로 선택한 교환성 매개변수(예: $f{\displaystyle }$= r ${\displaystyle {}_{}}$ ${\displaystyle T_{}}$ ${\$$GT$는 일반적으로 교환성 모수 추정치의 가독성을 높이기 위해 1의 값으로 설정된다(사용자가 선택한 교환성 모수에 대해 그러한 값을 표현할 수 있기 때문이다).$Q{\displaystyle }$ ${\displaystyle Q}$ 행렬이$$ 정규화되기 때문에 상대적인 용어로 교환성 매개변수를 표현하는 관행은 문제가 없다.정규화를 통해 매트릭스 지수 $P{\displaystyle (}$ ${\displaystyle t}$)${\displaystyle }$= e ${\displaystyle Q^{}}$ ${\displaystyle t^{}}$ ${\$의 $t{\displaystyle }$ ${\displaystyle t}($시간)를 부위별 예상 대체 단위로 표현할 수 있다$$(분자 혈전학 표준 실습).이는 돌연변이율 $[\displaystyle \mu }}$을(를) 1로$$ 설정하고 자유 매개변수 수를 8개로 줄인다는 진술과 맞먹는 것이다.구체적으로는 5개의 자유 교환성 매개변수($e$ ${\displaystyle a}$ ~ e ${\displaystyle$e})가 있으며$,$ $고정{\displaystyle }$f = ${\displaystyle r_{}}$ ${\displaystyle G_{}}$T = ${\displaystyle 1}${\$displaystyle f=r_{$에 대해 표현된다.이 예에서는$$ $GT}=1})$ 및 3개의 평형 기본 주파수 파라미터(위에서 설명한 바와 같이 $\pi {\displaystyle {}_{}}$ ${\displaystyle i_{}}$ ${\$ 값만$$ 지정하면 $\pi {\displaystyle \stackrel{}{}}$→ ${\$이(가) 1에 합해져야 하기 때문이다$$.

또한 대체 표기법은 GTR 모델의 하위 모델을 이해하기 쉽게 해주는데, 이는 단순히 교환성 및/또는 평형기준 주파수 파라미터가 동일한 값을 차지하도록 제약되는 경우에 해당한다.많은 특정 하위 모델들이 주로 원본 출판물에 기초하여 명명되었다.

분자 유전체학에서 종종 사용되는 DNA 진화의 선택된 모델

모델	교환성 매개변수	기본 주파수 파라미터	참조
JC69(또는 JC)	${\displaystyle a=b=c=d=e=f}$	${\displaystyle \pi _{A}=\pi _{C}=\pi _{G}=\pi _{T}=0.25}$	주크스와 칸토르(1969년)[5]
F81	${\displaystyle a=b=c=d=e=f}$	모든 $\pi {\displaystyle {}_{}}$ ${\displaystyle i_{}}$ ${\$ 값$$ 사용 가능	펠젠슈타인 (1981년)[28]
K2P(또는 K80)	${\displaystyle a}$= ${\displaystyle c}$= d${\displaystyle }$= ${\displaystyle f}$ ${\displaystyle a=c=d=f}($변환), ${\displaystyle b}$= e ${\displaystyle b=e}($변환)	${\displaystyle \pi _{A}=\pi _{C}=\pi _{G}=\pi _{T}=0.25}$	키무라 (1980년)[29]
HKY85	${\displaystyle a}$= ${\displaystyle c}$= d${\displaystyle }$= ${\displaystyle f}$ ${\displaystyle a=c=d=f}($변환), ${\displaystyle b}$= e ${\displaystyle b=e}($변환)	모든 $\pi {\displaystyle {}_{}}$ ${\displaystyle i_{}}$ ${\$ 값$$ 사용 가능	하세가와 외 연구진(1985)[30]
K3ST(또는 K81)	${\displaystyle }$$a{\displaystyle }$${\displaystyle }$= ${\displaystyle f}$ ${\displaystyle a=f$$}({\$displaystyle \properties } transversions$$), c${\displaystyle }$= ${\displaystyle d}$ ${\displaystyle c=d}($${\displaystyle }$ ${\displaystyle \$properties$$ $}),$ b${\displaystyle }$= ${\displaystyle e}$ ${\displaysty$ b$=e}($iops)	${\displaystyle \pi _{A}=\pi _{C}=\pi _{G}=\pi _{T}=0.25}$	키무라(1981년)[31]
TN93	${\displaystyle a}$= ${\displaystyle c}$= ${\displaystyle d}$ = f ${\displaystyle a=c=f}($변환), b${\displaystyle }${\$displaystyle b$${\displaystyle \}(<img\; alt="b"\; aria-hidden="true"\; class="mwe-math-fallback-image-inline"\; src="https://wikimedia.org/api/rest\_v1/media/math/render/svg/f11423fbb2e967f986e36804a8ae4271734917c3"\; style="vertical-align:\; -0.338ex;\; width:0.998ex;\; height:2.176ex;"\; papago-attr-id="325">A}${\$displaystyle A\왼쪽$ 화살표 $G}$ 전환$$), $e{\displaystyle }$ ${\displaysty$ e$}($${\displaystyle C}$ ${\displaystyle \pounds }$ T ${\displaystyle C\왼쪽$ 화살표 T$$$})$	모든 $\pi {\displaystyle {}_{}}$ ${\displaystyle i_{}}$ ${\$ 값$$ 사용 가능	타무라·[32]네이(1993)
SYM	모든 교환성 매개 변수 사용 가능	${\displaystyle \pi _{A}=\pi _{C}=\pi _{G}=\pi _{T}=0.25}$	자르키크 (1994년)[33]
GTR(또는 REV[24])	모든 교환성 매개 변수 사용 가능	모든 $\pi {\displaystyle {}_{}}$ ${\displaystyle i_{}}$ ${\$ 값$$ 사용 가능	타바레(1986)[22]

JC69^[5] 및 F81^[28] 모델(모든 교환성 매개변수가 동일한 경우)부터 SYM^[33] 모델 및 전체 GTR^[22](또는 REV^[24]) 모델(모든 교환성 매개변수가 자유로운 경우)^[34]에 이르기까지 교환성 매개변수를 GTR의 하위 모델을 형성하도록 제한할 수 있는 203가지 방법이 있다.The equilibrium base frequencies are typically treated in two different ways: 1) all ${\displaystyle \pi _{i}}$ values are constrained to be equal (i.e., ${\displaystyle \pi _{A}=\pi _{C}=\pi _{G}=\pi _{T}=0.25}$); or 2) all ${\displaystyle \pi _{i}}$ values are treated자유 매개 변수로서평형기준 주파수는 다른 방법으로는 대부분 제약될 수 있지만 생물학적 관점에서 모든 ${\displaystyle {link}_{}}$ i ${\$ 값은$$ 비현실적이다.The possible exception is enforcing strand symmetry^[35] (i.e., constraining ${\displaystyle \pi _{A}=\pi _{T}}$ and ${\displaystyle \pi _{C}=\pi _{G}}$ but allowing ${\displaystyle \pi _{A}+\pi _{T}\neq \pi _{C}+\pi _{G}}$).

대체 표기법은 또한 GTR 모델이 더 큰 상태 공간(예: 아미노산 또는 코돈)을 가진 생물학적 알파벳에 어떻게 적용될 수 있는지를 쉽게 알 수 있게 한다.평형 상태 주파수 집합은 $\pi {\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$ ${\$$\pi {\displaystyle {}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$ ${\$}}, $...$로 작성할 수 있다.${\displaystyle {\pi }_{}}$ ${\displaystyle k_{}}$ ${\$$displaystyle \pi _{k}}$ 및 $k$ {\$displaystyle r_$${ij$$}$ 문자$$ 상태의 모든 알파벳에 대한 교환성 파라미터 집합(r ${\displaystyle i_{}}$ ${\displaystyle j_{}}$ ${\$ r_{ij$\}\}).$These values can the be used to populate the ${\displaystyle Q}$ matrix by setting the off-diagonal elements as shown above (the general notation would be ${\displaystyle Q_{ij}=r_{ij}\pi _{j}}$), setting the diagonal elements ${\displaystyle Q_{ii}}$ to the negative sum of the off-diag동일 행의 온-온-요소 및 정규화.분명히 $k{\displaystyle }$= 아미노산의 경우$$ ${\displaystyle 20}$ ${\displaystyle k=20},$ 코돈의 경우$$ $k{\displaystyle }$= ${\displaystyle 61}$ ${\displaystyle k=61}($표준 유전자 코드를 가정)이다.그러나 아미노산에는 감소된 알파벳을 사용할 수 있기 때문에 이 표기법의 일반성이 이롭다.$예$를 들어${\displaystyle ,}$ k = 6 {\$displaystyle k=6}$을(를) 사용하고, 마가렛 데이호프가 제안한 ${\displaystyle \mathrm{6개}}$ 범주를 이용하여 아미노산을 재암호화하여 아미노산을 인코딩할 수 있다.감소된 아미노산 알파벳은 구성 변화 및 포화도의 영향을 감소시키는 방법으로 간주된다.^[36]

기계론적 대 경험적 모델

진화 모델의 주요 차이점은 검토 중인 데이터 세트에 대해 매회 얼마나 많은 매개변수를 추정하는지, 그리고 그 중 얼마나 많은 매개변수를 대규모 데이터 세트에서 한 번 추정하는지이다.기계론적 모델은 모든 대체를 분석된 모든 데이터 집합에 대해 추정되며, 가급적 최대우도를 사용하여 추정된 다수의 매개변수의 함수로 설명한다.이는 모델을 특정 데이터 세트의 특수성(예: DNA의 다른 구성 편향)에 맞게 조정할 수 있다는 장점이 있다.문제는 너무 많은 매개변수를 사용할 때 발생할 수 있으며, 특히 서로 보상할 수 있는 경우(이는 식별 불가능으로^[37] 이어질 수 있음) 문제가 발생할 수 있다.따라서 데이터 세트가 너무 작아서 모든 모수를 정확하게 추정하기에 충분한 정보를 산출할 수 없는 경우가 많다.

경험적 모형은 큰 데이터 집합에서 많은 매개변수(일반적으로 문자 빈도뿐만 아니라 속도 행렬의 모든 항목, 위의 GTR 모델 참조)를 추정하여 생성된다.이 매개변수는 고정되며 모든 데이터 집합에 재사용된다.이는 그러한 매개변수를 더 정확하게 추정할 수 있다는 장점이 있다.일반적으로 현재 데이터 집합에서만 대체 행렬의 모든 항목을 추정할 수 있는 것은 아니다.단점에서는 교육 데이터에서 추정된 매개변수가 너무 일반적이어서 특정 데이터 집합에 적합하지 않을 수 있다.이 문제에 대한 잠재적 해결책은 최대우도(또는 다른 방법)를 사용하여 데이터로부터 일부 모수를 추정하는 것이다.단백질 진화에 관한 연구에서는 평형 아미노산 $주파수{\displaystyle \stackrel{}{}}$ ${\displaystyle \stackrel{}{\to }}$→ =${\displaystyle }$( a ${\displaystyle {}_{}}$, ${\displaystyle r_{}}$ R${\displaystyle {}_{}}$, ${\displaystyle n_{}}$N${\displaystyle }$, . . ${\displaystyle v_{}}$ V${\displaystyle {}_{}}$) ${\displaystyle {\vec{\pi }}}=(\pi$_{$A},\pi _{R},\pi$ _${N},$ ...}...$\pi _{V}($아미노산의 평형 주파수를 나타내기 위해 1글자 IUPAC 코드를 사용하여)는 교환성 매트릭스를 고정하면서 데이터로부터^[38] 추정하는 경우가 많다.데이터로부터 아미노산 주파수를 추정하는 일반적인 관행을 넘어, 단백질 진화를 위해 교환성^[39]$$파라미터를 추정하거나 $Q{\displaystyle }$ {\$displaystyle Q}$ 행렬을$$^[40] 다른 방법으로 조정하는 방법이 제안되었다.

대규모 게놈 염기서열 분석은 여전히 매우 많은 양의 DNA와 단백질 염기서열을 생성하므로, 경험적 코돈 모델을 포함하여 어떤 수의 매개변수를 가진 경험적 모델을 만들 수 있는 충분한 데이터가 있다.^[41]위에서 언급한 문제들 때문에, 대부분의 매개변수를 대규모 데이터에 한 번 추정함으로써, 두 가지 접근방식이 결합되는 경우가 많은 반면, 몇 가지 남은 매개변수는 고려 중인 데이터 세트로 조정된다.다음 절에는 DNA, 단백질 또는 코돈 기반 모델에 대해 취해진 다양한 접근방식에 대한 개요가 수록되어 있다.

DNA 대체 모델

DNA 진화의 첫 모델은 1969년 쥬크스와 캔터사가^[5] 제안되었다.Jukes-Canter(JC 또는 JC69) 모델은 모든 베이스에 대해 동일한 평형 주파수와 동일한 전환 속도를 가정하며 GTR 모델의 가장 단순한 하위 모델이다.1980년에 기무라 모투는 전환용과 변환률용 2개의 매개변수(K2P 또는 K80^[29])를 가진 모델을 도입했다.1년 후, 기무라 3대체 형식. 하나는 전이율에, 하나는 strong/weak 속성(↔ T{A\leftrightarrow T\displaystyle}, C↔ G{\displaystyle C\leftrightarrow G}, 지정된 β{\disp 보존하는 것 transversions의 비율을 위한 것과 두번째 모델(K3ST, K3P, 또는 K81[31일])을 소개했다.놓다$스타일 \beta }$ 기무라$$^[31]) 및 뉴클레오티드의 아미노/케토 특성을 보존하는 트랜스퍼션 비율(${\displaystyle }$^[31](기무라$$) 1파운드 $displaystyle A\leftrightarrow C}$ 및 $G파운드$ T$[\displaysty$ $G$$\leftrigharrow$ $T$$})$에 $대한{\displaystyle }$ 것$.$1981년, Joseph Felsenstein은 대체 비율이 표적 핵분열체의 평형 주파수에 해당하는 4-모수 모델(F81^[28])을 제안했다.하세가와, 기시노, 야노는 마지막 두 모델을 5변수 모델(HKY^[30])으로 통일했다.이러한 선구적 노력 이후 1990년대에 GTR 모델의 많은 추가 하위 모델이 문헌(및 일반용도)에 도입되었다.^[32][33]구체적인 방법으로 GTR 모델을 넘어서는 다른 모델들도 여러 연구자들에 의해 개발되고 다듬어졌다.^[42][43]

거의 모든 DNA 대체 모델은 (위에서 설명한 바와 같이) 기계론적 모델이다.이러한 모형에 대해 추정해야 하는 모수의 수가 적기 때문에 데이터에서 그러한 모수를 추정할 수 있다.DNA 염기서열 진화의 패턴이 유기체와 유기체 내 유전자에 따라 다른 경우가 많기 때문에 또한 필요하다.후자는 특정 목적을 위한 선택 작용(예: 빠른 표현 또는 메신저 RNA 안정성)에 의한 최적화를 반영하거나 대체 패턴의 중립적 변화를 반영할 수 있다.따라서 유기체와 유전자의 종류에 따라 이러한 상황에 맞게 모델을 조정할 필요가 있을 것 같다.

2-상태 대체 모델

DNA 염기서열 데이터를 분석하는 다른 방법은 뉴클레오티드를 청진(R)과 피리미딘(Y)으로 재코딩하는 것이다.^[44][45] 이러한 관행을 흔히 RY-코딩이라고 한다.^[46]다중 시퀀스 정렬에서 삽입 및 삭제도 이진 데이터로^[47] 인코딩하여 2-상태 모델을 사용하여 분석할 수 있다.^[48][49]

시퀀스 진화의 가장 간단한 2개 상태 모델은 캐번더-파리스 모델 또는 캐번더-파리스-네이만(CFN) 모델이라고 불린다. 이 모델의 이름은 그것이 여러 다른 출판물에 독립적으로 설명되었다는 사실을 반영한다.^[50][51][52]The CFN model is identical to the Jukes-Cantor model adapted to two states and it has even been implemented as the "JC2" model in the popular IQ-TREE software package (using this model in IQ-TREE requires coding the data as 0 and 1 rather than R and Y; the popular PAUP* software package can interpret a data matrix comprising only R and Y as data to CFN 모델을 사용하여 분석한다).계통발생학 하다마드 변환을 이용해 2진수 데이터를 분석하는 것도 간단하다.^[53]대안적인 2-상태 모델은 단일 자유 매개변수를 추가하여 R과 Y (또는 0과 1)의 평형주파수 매개변수가 0.5 이외의 값을 취할 수 있도록 한다. 이 모델을 다양하게^[44] CFU 또는 GTR2(IQ-TREE)라고 부른다.

아미노산 치환 모델

많은 분석, 특히 더 긴 진화 거리의 경우 진화는 아미노산 수준에 따라 모델링된다.모든 DNA 대체물이 인코딩된 아미노산을 바꾸는 것은 아니기 때문에 뉴클레오티드 베이스 대신 아미노산을 볼 때 정보가 손실된다.그러나, 몇 가지 장점은 아미노산 정보 사용에 찬성한다: DNA는 아미노산보다 구성적 편향성을 보이는 경향이 훨씬 더 높으며, DNA의 모든 위치가 같은 속도로 진화하는 것은 아니다(비동기 돌연변이는 동의어보다 모집단에 고정될 가능성이 적다). 그러나 아마도 그것들 때문에 가장 중요한 것일 것이다.빠른 진화의 위치와 제한된 알파벳 크기(가능한 4개 상태만 가능), DNA는 더 많은 후방 대체에 시달려 진화적인 더 긴 거리를 정확하게 추정하기 어렵다.

DNA 모델과 달리 아미노산 모델은 전통적으로 경험적 모델이다.이들은 데이호프와 동료들에 의해 1960년대와 1970년대에 적어도 85%의 정체성을 가진 단백질 정렬에서 대체율을 추정함으로써 개척되었다(원래는 데이터가^[54] 매우 제한되어 있고 결국 1978년의^[55] 데이호프 PAM 모델에서 정점을 찍었다).이를 통해 현장에서 여러 대체물을 관찰할 수 있는 가능성을 최소화했다.추정된 비율 매트릭스에서 PAM250과 같은 이름으로 알려진 일련의 대체 확률 매트릭스가 도출되었다.왜냐하면 블로섬 매트릭스 더 진화적 거리읜 다양한 민감하게, PAMlog-odds 매트릭스와는 달리 나타나지만 블로섬 matrices[56]이 컨텍스트에 있는 PAMlog-odds 매트릭스 대체되고 있Log-odds 매트릭스는 Dayhoff PAM에게 법적 모델에 기반한 일반적으로 상동 순서 검색 결과의 중요성을 평가하기 위한, 사용되었다.[57]

데이호프 PAM 매트릭스는 단백질 데이터를^[58] 사용한 혈류 발생의 첫 번째 최대 우도 분석 중 하나에 사용된 교환성 매개변수의 출처였으며 PAM 모델(또는 DCMut라고^[59] 하는 PAM 모델의 개선 버전)은 혈류 발생학에서 계속 사용된다.그러나 PAM 모델을 생성하기 위해 사용된 한정된 정렬 수(1970년대에 사용 가능한 제한된 시퀀스 데이터의 양을 반영)는 거의 확실히 일부 속도 매트릭스 파라미터의 분산을 부풀렸다(대안적으로 PAM 모델을 생성하기 위해 사용된 단백질은 대표적이지 않은 집합일 수 있음).그럼에도 불구하고 PAM 모델이 더 현대적인 경험적 모델만큼 대부분의 데이터셋에 잘 맞는 경우는 거의 없다는 것은 분명하다(Keane et al. 2006^[60]) (Keane et al. 2006)는 수천 개의 척추동물, 프로테오박테리아, 고고학적 단백질을 시험했고 그들은 데이호프 PAM 모델이 최대 <4%의 단백질에 가장 잘 맞는다고 밝혔다.

1990년대부터 시퀀스 기술의 향상으로 시퀀스 데이터베이스의 급속한 확장이 많은 새로운 경험적 매트릭스를 추정하게 되었다(전체 목록은 참조).초기 노력에서는 새로운 로그-오드 매트릭스와^[62] JTT(Jones-Taylor-Thornton) 모델을 생성하기 위해 단백질 데이터베이스의 대규모 매칭을 사용하여 데이호프가 사용하는 방법과 유사한 방법을 사용했다.^[63]이 시기 동안 컴퓨팅 파워의 급속한 증가(무어의 법칙과 같은 반영 요소)는 최대우도(예: WAG^[38] 및 LG^[64] 모델)와 기타 방법(예: VT^[65] 및 PMB^[66] 모델)을 사용하여 경험적 모델에 대한 매개변수를 추정할 수 있게 했다.

NCM(공통 메커니즘) 모델 및 최대 구문 분석

1997년, 터플리와^[67] 스틸은 공통 메커니즘(No common mechanism, NCM) 모델명을 붙인 모델을 설명했다.NCM 모델이 주어진 특정 데이터 집합의 최대우도 트리의 토폴로지는 최대 구문 분석 기준이 주어진 동일한 데이터에 대한 최적 트리의 토폴로지와 동일하다.NCM 모델은 모든 데이터(예: 동질 뉴클레오티드, 아미노산 또는 형태론적 문자)가 공통 계통생성 트리에 의해 관련된다고 가정한다.$그런{\displaystyle }$ 다음 각 동음이의 문자마다 2 ${\displaystyle T}$- ${\displaystyle 3}$ ${\displaystyle$ 2T-3$} 매개$ 변수가 도입되며$$, 여기서 T ${\displaystyle T}$은 시퀀스 수입니다.이는 데이터 집합의 모든 문자 × 분기 쌍에 대해 별도의 속도 매개변수를 추정하는 것으로 볼 수 있다(완전하게 분해된 계통생성 트리의 분기 수는 ${\displaystyle 2}$ ${\displaystyle \mathrm{T}}$- 3 ${\displaystyle 2T-3}).$따라서 NCM 모델의 자유 매개변수 수는 항상 데이터 매트릭스의 동음이의 문자 수를 초과하며, NCM 모델은 일관되게 "과대변수"라는 비판을 받아왔다.^[68]

참조

외부 링크

• 아미노산 치환 실험모델

메모들