유한 상태 기계

유한 상태 기계(FSM) 또는 유한 상태 오토마타(FSA, 복수: 오토마타), 유한 상태 오토마타 또는 단순히 상태 기계는 계산의 수학적 모델입니다.그것은 주어진 시간에 유한한 수의 상태들 중 하나에 정확히 있을 수 있는 추상적인 기계입니다.FSM은 일부 입력에 응답하여 한 상태에서 다른 상태로 변경될 수 있습니다. 한 상태에서 다른 상태로 변경하는 것을 전환이라고 합니다.^[1]FSM은 해당 상태, 초기 상태 및 각 전환을 트리거하는 입력의 목록에 의해 정의됩니다.유한 상태 기계는 결정론적 유한 상태 기계와 비결정론적 유한 상태 기계의 두 가지 유형입니다.^[2]비결정론적 유한 상태 기계에 대해서는 동등한 결정론적 기계를 구성할 수 있습니다.

상태 기계의 행동은 현대 사회의 많은 장치에서 관찰될 수 있는데, 이 장치는 일련의 사건에 따라 미리 정해진 일련의 행동을 수행합니다.간단한 예로는 동전의 적절한 조합이 입금되면 제품을 제공하는 자동판매기, 정류장 순서가 탑승자가 요청하는 층에 따라 결정되는 엘리베이터, 자동차가 대기할 때 순서를 바꾸는 신호등, 숫자 순서를 올바른 순서로 입력해야 하는 조합 잠금 장치 등이 있습니다.

유한 상태 기계는 튜링 기계와 같은 다른 계산 모델보다 계산 능력이 낮습니다.^[3]계산력 구별은 튜링 기계는 할 수 있지만 FSM은 할 수 없는 계산 작업이 있음을 의미합니다.이것은 FSM의 메모리가 보유한 상태 수에 따라 제한되기 때문입니다.유한 상태 기계는 머리가 "읽기" 연산만 수행할 수 있도록 제한된 튜링 기계와 동일한 계산 능력을 가지며 항상 왼쪽에서 오른쪽으로 이동해야 합니다.FSM은 오토마타 이론의 보다 일반적인 분야에서 연구됩니다.

예: 동전으로 작동하는 개찰구

상태 기계에 의해 모델링될 수 있는 간단한 메커니즘의 예는 개찰구입니다.^[4][5]지하철과 놀이공원의 놀이기구에 대한 접근을 통제하기 위해 사용되는 개찰구는 하나는 진입로를 가로질러 하나는 허리 높이로 세 개의 회전하는 팔이 있는 문입니다.처음에는 팔이 잠겨서 출입구를 막고, 손님들이 지나갈 수 없도록 했습니다.개찰구의 슬롯에 동전이나 토큰을 넣으면 암이 잠금 해제되어 한 명의 고객이 통과할 수 있습니다.고객이 지나가면 다른 동전이 들어갈 때까지 암이 다시 잠깁니다.

상태 기계로 간주되는 개찰구는 다음과 같은 두 가지 가능한 상태가 있습니다.잠김과 잠김.^[4]그 상태에 영향을 미치는 두 가지 가능한 입력이 있습니다: 슬롯(코인)에 동전을 넣는 것과 팔을 밀어 넣는 것입니다.잠금 상태에서 암을 누르는 것은 아무런 영향을 주지 않으며, 입력 푸시를 아무리 많이 해도 암은 잠금 상태를 유지합니다.동전을 넣으면(즉, 기계에 동전을 입력하면) 상태가 잠금에서 해제로 바뀝니다.잠금이 해제된 상태에서 추가 코인을 투입해도 효과가 없습니다. 즉, 추가 코인 투입을 해도 상태가 변경되지 않습니다.하지만 고객이 암을 밀면서 푸시 입력을 하면 상태가 다시 잠금 상태로 전환됩니다.

개찰구 상태 기계는 각각의 가능한 상태, (기계에 제공된 입력에 기초하여) 그들 사이의 전환 및 각 입력에 의한 출력을 보여주는 상태 전이 표로 나타낼 수 있습니다.

현재 상태	인풋	다음 상태	산출량
잠김	동전을	잠금 해제됨	고객이 통과할 수 있도록 개찰구의 잠금을 해제합니다.
	밀다	잠김	없음.
잠금 해제됨	동전을	잠금 해제됨	없음.
	밀다	잠김	고객이 통과하면 개찰구를 잠급니다.

개찰구 상태 기계는 상태도(위)라고 하는 지시 그래프로 나타낼 수도 있습니다.각 상태는 노드(circle)로 표시됩니다.가장자리(화살표)는 한 상태에서 다른 상태로의 전환을 보여줍니다.각 화살표는 해당 전환을 트리거하는 입력으로 레이블이 지정됩니다.상태 변경을 유발하지 않는 입력(예: 잠금 해제 상태의 코인 입력)은 원래 상태로 돌아가는 원형 화살표로 표시됩니다.검은 점에서 Locked(잠금) 노드로 들어가는 화살표는 초기 상태임을 나타냅니다.

개념 및 용어

상태는 전환을 실행하기 위해 대기 중인 시스템의 상태에 대한 설명입니다.전환은 조건이 충족되거나 이벤트가 수신될 때 실행할 동작 집합입니다.예를 들어 오디오 시스템을 사용하여 라디오를 들을 때(시스템이 "라디오" 상태임), "다음" 자극을 받으면 다음 스테이션으로 이동합니다.시스템이 "CD" 상태일 때 "다음" 자극은 다음 트랙으로 이동합니다.동일한 자극은 현재 상태에 따라 다른 행동을 유발합니다.

일부 유한 상태 시스템 표현에서는 동작을 상태와 연결할 수도 있습니다.

• 진입 작업: 상태를 입력할 때 수행합니다.
• 종료 작업: 상태를 종료할 때 수행됩니다.

표현

상태/이벤트 테이블

여러 가지 상태 전이 테이블 유형이 사용됩니다.가장 일반적인 표현은 다음과 같습니다. 현재 상태(예: B)와 입력(예: Y)의 조합은 다음 상태(예: C)를 나타냅니다.전체 작업의 정보는 표에 직접 설명되어 있지 않으며 각주를 사용하여 추가할 수 있습니다.^{[further explanation needed]}전체 작업의 정보를 포함하는 FSM 정의는 상태 테이블을 사용하여 가능합니다(가상 유한 상태 시스템도 참조).

상태 전이표

현재의 주 인풋	A주	주 B	주 C
입력X	...	...	...
입력 Y	...	주 C	...
입력 Z	...	...	...

UML 상태 기계

Unified Modeling Language에는 상태 시스템을 설명하는 표기법이 있습니다.UML 상태 기계는 기존 유한 상태 기계의 한계를^{[citation needed]} 극복하면서도 주요 이점을 유지합니다.UML 상태 기계는 동작의 개념을 확장하면서 계층적으로 중첩된 상태와 직교 영역의 새로운 개념을 도입합니다.UML 상태 기계는 Mealy 기계와 Moore 기계의 특성을 모두 가지고 있습니다.Mealy 시스템에서와 같이 시스템의 상태와 트리거 이벤트에 모두 의존하는 작업과 Moore 시스템에서와 같이 전환보다는 상태와 관련된 진입 및 퇴출 작업을 지원합니다.^{[citation needed]}

SDL 상태 시스템

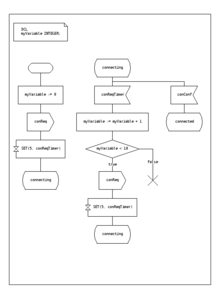
사양 및 설명 언어는 ITU의 표준으로 전환 시 동작을 설명하기 위한 그래픽 기호가 포함되어 있습니다.

• 이벤트를 보내다
• 이벤트를 받다
• 타이머를 걸다
• 타이머를 끊다
• 다른 동시 상태 시스템 시작
• 결정

SDL은 "추상 데이터 유형"이라는 기본 데이터 유형과 동작 언어, 실행 시맨틱을 내장하여 유한 상태 머신을 실행할 수 있도록 합니다.^{[citation needed]}

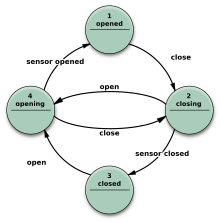
기타 상태도

그림 3과 같은 FSM을 나타내는 많은 변형이 있습니다.

사용.

유한 상태 기계는 여기에 제시된 반응형 시스템 모델링에 사용되는 것 외에도 전기 공학, 언어학, 컴퓨터 과학, 철학, 생물학, 수학, 비디오 게임 프로그래밍 및 논리학 등 다양한 분야에서 중요합니다.유한 상태 기계는 오토마타 이론과 계산 이론에서 연구되는 오토마타의 한 종류입니다.컴퓨터 과학에서 유한 상태 기계는 응용 행동 모델링(제어 이론), 하드웨어 디지털 시스템 설계, 소프트웨어 엔지니어링, 컴파일러, 네트워크 프로토콜 및 컴퓨터 언어학에 널리 사용됩니다.

분류

유한 상태 기계는 수용기, 분류기, 변환기 및 시퀀서로 세분화될 수 있습니다.^[6]

억셉터즈

수신기(검출기 또는 인식기라고도 함)는 수신된 입력이 허용되는지 여부를 나타내는 이진 출력을 생성합니다.수락자의 각 상태는 수락 또는 수락하지 않습니다.모든 입력이 수신되면 현재 상태가 수락 상태이면 입력이 수락되고 그렇지 않으면 거부됩니다.규칙적으로 입력은 기호(문자)의 시퀀스이며, 동작은 사용되지 않습니다.시작 상태는 수락 상태일 수도 있으며, 이 경우 수락자는 빈 문자열을 수락합니다.그림 4의 예는 "nice" 문자열을 받아들이는 수락자를 보여줍니다.이 수용체에서 유일한 수용 상태는 상태 7입니다.

(아마도 무한한) 기호 수열 집합은 공식 언어라고 불리며, 만약 그 집합을 정확히 받아들이는 수용체가 있다면 일반 언어입니다.예를 들어 0이 짝수인 이진 문자열의 집합은 정규 언어(cf)입니다.도 5), 길이가 소수인 모든 문자열의 집합은 그렇지 않은 경우.^{[7]: 18, 71}

승인자는 승인자가 승인한 모든 문자열을 포함하지만 거부된 문자열은 포함하지 않는 언어를 정의하는 것으로 설명될 수 있습니다. 해당 언어는 승인자가 승인합니다.정의상 수용자가 수용하는 언어는 일반 언어입니다.

주어진 수용체에 의해 수용된 언어를 결정하는 문제는 대수 경로 문제의 한 예이며, 그 자체는 (임의) 반올림의 요소로 가중된 에지를 갖는 그래프로 최단 경로 문제를 일반화합니다.^{[8][9][jargon]}

그림 5: 이진 입력 문자열이 짝수 개의 0을 포함하는지 여부를 감지하는 결정론적 유한 자동화(DFA)는 수용 상태의 예를 보여줍니다.

S₁(시작 상태)는 짝수 개의 0이 입력된 상태를 나타냅니다.따라서 S는₁ 허용 상태입니다.이진 문자열에 짝수 개의 0이 포함된 경우(0이 포함되지 않은 이진 문자열 포함), 이 수락자는 수락 상태로 종료됩니다.이 수용기에 의해 수용되는 문자열의 예는 ε(빈 문자열), 1, 11, 11..., 00, 010, 1010, 10110 등입니다.

분류자

분류기는 n이 엄밀하게 2보다 큰 n-ary 출력을 생성하는 수용기의 일반화입니다.^[10]

트랜스듀서

변환기는 동작을 사용하여 주어진 입력 및/또는 상태에 기초하여 출력을 생성합니다.제어 응용 분야와 컴퓨터 언어학 분야에서 사용됩니다.

제어 응용 프로그램에서는 두 가지 유형으로 구분됩니다.

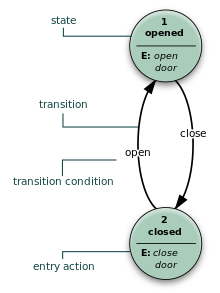
무어머신

FSM은 엔트리 동작만 사용합니다. 즉, 출력은 상태에 따라서만 달라집니다.무어 모델의 장점은 행동을 단순화하는 것입니다.엘리베이터 문을 생각해 보세요.상태 시스템은 상태 변경을 트리거하는 "command_open"과 "command_close"의 두 가지 명령을 인식합니다."Opening" 상태의 엔트리 동작(E:)은 도어를 여는 모터를 시작하고, "Closing" 상태의 엔트리 동작은 도어를 닫는 다른 방향의 모터를 시작합니다."열림" 및 "닫힘" 상태는 완전히 열리거나 닫히면 모터를 정지시킵니다."문이 열려 있습니다" 또는 "문이 닫혀 있습니다"라는 상황을 외부 세계(예: 다른 상태 기계)에 알립니다.

밀기

FSM은 또한 입력 동작을 사용합니다. 즉, 출력은 입력과 상태에 따라 달라집니다.Mealy FSM을 사용하면 종종 상태 수가 줄어듭니다.그림 7의 예는 무어 예에서와 동일한 동작을 구현한 Mealy FSM을 보여줍니다(동작은 구현된 FSM 실행 모델에 따라 달라지며 가상 FSM에서는 작동하지만 이벤트 중심 FSM에서는 작동하지 않습니다).입력 동작은 "command_close가 도착하면 도어를 닫기 위해 모터를 시작"하고 "command_open이 도착하면 도어를 열기 위해 다른 방향으로 모터를 시작"하는 두 가지입니다."열림" 및 "닫힘" 중간 상태는 표시되지 않습니다.

시퀀서

시퀀서(생성기라고도 함)는 단일 문자 입력 알파벳을 가진 수용기 및 변환기의 하위 클래스입니다.이들은 수용기 또는 변환기 출력의 출력 시퀀스로 볼 수 있는 하나의 시퀀스만 생성합니다.^[6]

결정론

결정론적 오토마타(DFA)와 비결정론적 오토마타(NFA, GNFA) 사이의 또 다른 차이입니다.결정론적 자동화에서 모든 상태는 가능한 각 입력에 대해 정확히 하나의 전이를 가집니다.비결정론적 오토마톤에서 입력은 주어진 상태에 대해 하나 이상, 또는 하나 이상의 전환을 초래할 수 있습니다.파워셋 구성 알고리즘은 모든 비결정적 자동화를 동일한 기능을 가진 (일반적으로 더 복잡한) 결정적 자동화로 변환할 수 있습니다.

하나의 상태만을 갖는 유한 상태 기계를 "조합형 FSM"이라고 합니다. 이 기계는 상태로 전환할 때에만 동작을 허용합니다.이 개념은 다수의 유한 상태 기계가 함께 작동해야 하는 경우와 설계 도구에 적합한 FSM의 한 형태로서 순수하게 결합적인 부분을 고려하는 것이 편리할 때 유용합니다.^[11]

대안적 의미론

상태 시스템을 나타내는 데 사용할 수 있는 다른 의미론 집합이 있습니다.예를 들어, 임베디드 컨트롤러의 로직을 모델링하고 설계하는 도구가 있습니다.^[12]이들은 계층적 상태 기계(일반적으로 둘 이상의 현재 상태를 가짐), 플로우 그래프 및 진리표를 하나의 언어로 결합하여 다른 형식주의 및 의미론 집합을 생성합니다.^[13]이러한 차트는 Harrel의 원래 상태 시스템과 마찬가지로 ^[14]계층적으로 중첩된 상태, 직교 영역, 상태 작업 및 전환 작업을 지원합니다.^[15]

수학적 모형

일반적인 분류에 따라 다음과 같은 공식적인 정의가 있습니다.

결정론적 유한 상태 기계 또는 결정론적 유한 상태 수용체는 5중 (σ${\displaystyle ,}$ ${\displaystyle S,}$ ${\displaystyle {s0}_{}}$ δ${\displaystyle ,}$ ${\displaystyle F)}$ ${\displaystyle (\Sigma,S,s_{0},\delta,F)}$이며$,$ 여기서:

• ${\displaystyle$ \Sigma$}$은(는) 입력 알파벳(유한 비어 있지 않은 기호 집합)입니다.
• ${\displaystyle S}$ ${\displaystyle S}$은(는) 유한한 비어 있지 않은 상태 집합입니다.
• ${\displaystyle s_{}}$ ${\displaystyle {0\mathrm{}}_{}}$ ${\$은(는) $초기{\displaystyle }$ 상태$,$ S {\$displaystyle S}$의 요소입니다$;$
• ${\displaystyle }${\$displaysty$ ${\displaystyle \}}$은(는) 상태 전이 함수입${\displaystyle 니}$다. ${\displaystyle \delta }$ : ${\displaystyle S}$ ${\displaystyle \times }$${\displaystyle \mathrm{\sigma }}$ S ${\displaysty$${\displaystyle \mathrm{le\; \backslash d}}$$elta$ :$S\times \Sigma \rightarrow S}$ (비결정론적 유한 자동화에서는 $δ$일 것입니다:$$× $σ$ $→$ ${\displaystyle P}$ ( S${\displaystyle$ :$S\times \Sigma \rightarrow {\mathcal {P}}(S),$즉 $δ$ ${\displaystyle \delta}$이(가) 상태 집합을 반환합니다.
• ${\displaystyle F}$ ${\displaystyle F}$은 $S{\displaystyle }$ ${\displaystyle$ S$}$의 ($아마도$ 비어 있는) 부분 집합인 최종 상태 집합입니다$.$

결정론적 FSM과 비결정론적 FSM 모두에서 ${\displaystyle \delta }$ δ을 부분 함수로 허용하는 것이 일반적입니다. 즉, δ${\displaystyle }$($s$ x$)$ ${\displaystyle s$$\in$ $S}$ $및$ x σ ∈ ${\displaystyle$ x$\in \sigma}$의 모든 조합에 대해 ∈ {\displaystyle M}을$($를) 정의할 필요는 없습니다$.$ $FSM$ M$${\$displaystyle$ M$}$이(가) s $상태$ ${\di$$spaystyles$ 다음 기호는 $x$ ${\displaystyle x}$이고 $δ$${\displaystyle (s,}$ x${\displaystyle )}$ ${\displaystyle \delta(s,x)}$이(가) 정의되지 않았습니다. 그러면 $M$ ${\displaystyle M}$이(가) 오류를 알릴 수 있습니다(즉, 입력 거부).일반 상태 시스템의 정의에서는 유용하지만, 시스템을 변환할 때는 덜 유용합니다.기본 형태의 일부 알고리즘에는 총 함수가 필요할 수 있습니다.

유한 상태 기계는 머리가 "읽기" 연산만 수행할 수 있도록 제한된 튜링 기계와 동일한 계산 능력을 가지며 항상 왼쪽에서 오른쪽으로 이동해야 합니다.즉, 유한 상태 기계에 의해 받아들여지는 각각의 형식 언어는 그러한 종류의 제한된 튜링 기계에 의해 받아들여지고, 그 반대의 경우도 마찬가지입니다.^[16]

유한 상태 변환기는 6중$($σ,${\displaystyle }$γ, ω${\displaystyle ,}$ ${\displaystyle S,}$ ${\displaystyle {s0}_{}}$ δ${\displaystyle ,}$ ω${\displaystyle )}$ ${\displaystyle(\Sigma,\Gamma,S,s_{0},\delta,\omega )}$이며$,$ 여기서:

• ${\displaystyle$ \Sigma$}$은(는) 입력 알파벳(유한 비어 있지 않은 기호 집합)입니다.
• ${\displaystyle \mathrm{}}${\$displaystyle$ \$Gamma}$은(는) 출력 알파벳(유한 비어 있지 않은 기호 집합)입니다.
• ${\displaystyle S}$ ${\displaystyle S}$은(는) 유한한 비어 있지 않은 상태 집합입니다.
• ${\displaystyle s_{}}$ ${\displaystyle {0\mathrm{}}_{}}$ ${\$은 S {\$displaystyle S}$의 요소인 초기 상태입니다$.$
• ${\displaystyle }${\$displaysty$ ${\displaystyle \}}$은(는) 상태 전이 함수입${\displaystyle 니}$다. ${\displaystyle \delta }$ : ${\displaystyle S}$ ${\displaystyle \times }$${\displaystyle \mathrm{\sigma }}$ S ${\displaysty$${\displaystyle \mathrm{le\; \backslash d}}$$elta$ :$S\times \Sigma \rightarrow S$
• ${\displaystyle }${\$displaystyle \omega$}이$($가) 출력 함수입니다.

출력 기능이 상태 및 입력 기호(ω : S ×${\displaystyle }$σ${\displaystyle }$→ γ ${\displaystyle \omega$:$S\times \Sigma \rightarrow \Gamma$ 정의는 Mealy 모델에 해당하며 Mealy 기계로 모델링할 수 있습니다.출력 기능이 상태에만 의존하는 경우( ω :${\displaystyle S}$ → γ ${\displaystyle \omega$:$S\rightarrow \Gamma$ 정의는 무어 모델에 해당하며 무어 기계로 모델링할 수 있습니다.반자동화(semiautomaton) 또는 전이(transition) 시스템은 출력 기능이 전혀 없는 유한 상태 기계입니다.

무어 기계의 첫 번째 출력 기호인 ω ${\displaystyle ({}_{}}$ ${\displaystyle 0_{}}$ ${\displaystyle \omega (s_{0})}$를 무시하면 대상 무어 상태의 출력 기호로 모든 Mealy 전환의 출력 함수(즉, 모든 에지에 라벨링)를 설정하여 출력 등가 Mealy 기계로 쉽게 변환할 수 있습니다$.$Mealy 기계 상태는 들어오는 변환(에지)에서 출력 레이블이 다를 수 있기 때문에 역변환은 덜 간단합니다.이러한 모든 상태는 사고 출력 기호마다 하나씩 여러 무어 기계 상태로 나누어져야 합니다.^[17]

최적화

FSM을 최적화한다는 것은 동일한 기능을 수행하는 상태의 수가 최소인 기계를 찾는 것을 의미합니다.이를 수행하는 가장 빠른 알고리즘은 Hopcroft 최소화 알고리즘입니다.^[18][19]다른 기법으로는 암시표를 사용하거나 무어 축소 절차를 사용하는 것이 있습니다.^[20]또한, 비순환적 FSA는 선형 시간으로 최소화될 수 있습니다.^[21]

실행

하드웨어 응용 프로그램

디지털 회로에서 FSM은 프로그래밍 가능한 논리 장치, 프로그래밍 가능한 논리 제어기, 논리 게이트 및 플립 플롭 또는 릴레이를 사용하여 제작될 수 있습니다.보다 구체적으로, 하드웨어 구현은 상태 변수들을 저장하는 레지스터, 상태 전이를 결정하는 조합 로직 블록 및 FSM의 출력을 결정하는 두 번째 조합 로직 블록을 필요로 합니다.고전적인 하드웨어 구현 중 하나가 Richards 컨트롤러입니다.

메드베데프 기계에서 출력은 상태 플립플롭에 직접 연결되어 플립플롭과 출력 사이의 시간 지연을 최소화합니다.^[22][23]

저전력 상태 기계에 대한 관통 상태 인코딩은 전력 소모를 최소화하기 위해 최적화될 수 있습니다.

소프트웨어 응용 프로그램

유한 상태 기계로 소프트웨어 응용 프로그램을 구축하는 데 일반적으로 사용되는 개념은 다음과 같습니다.

• 오토마타 기반 프로그래밍
• 이벤트 구동 유한 상태 기계
• 가상 유한 상태 기계
• 상태설계패턴

유한 상태 기계 및 컴파일러

유한 오토마타는 종종 프로그래밍 언어 컴파일러의 프론트엔드에 사용됩니다.이러한 프론트엔드는 어휘 분석기 및 파서를 구현하는 여러 개의 유한 상태 기계로 구성될 수 있습니다.어휘 분석기는 일련의 문자에서 시작하여 일련의 언어 토큰(예: 예약된 단어, 리터럴 및 식별자)을 작성하며, 이를 통해 파서는 구문 트리를 작성합니다.어휘 분석기와 파서는 프로그래밍 언어의 문법에서 규칙적이고 문맥이 없는 부분을 처리합니다.^[24]

참고 항목

참고문헌

추가열람

일반적

• Sakarovitch, Jacques (2009). Elements of automata theory. Translated from the French by Reuben Thomas. Cambridge University Press. ISBN 978-0-521-84425-3. Zbl 1188.68177.
• Wagner, F., "유한 상태 기계를 갖는 모델링 소프트웨어: 실용적 접근법", Auerbach Publications, 2006, ISBN 0-8493-8086-3
• ITU-T, 권장 Z.100 규격 및 설명 언어(SDL)
• Samek, M., C/C++, CMP Books, 2002, ISBN 1-57820-110-1.
• Samek, M., Practical UML State chart in C/C++, 2nd Edition, Newnes, 2008, ISBN 0-7506-8706-1
• Gardner, T., Wayback Machine에서 2008-11-19 고급 상태 관리 보관, 2007
• Cassandras, C., Laforte, S., "불연속 이벤트 시스템 소개"Kluwer, 1999, ISBN 0-7923-8609-4.
• Timothy Kam, 유한 상태 기계의 합성: 기능 최적화.Kluwer Academic Publishers, Boston 1997, ISBN 0-7923-9842-4
• Tiziano Villa, 유한 상태 기계의 합성: 논리 최적화Kluwer Academic Publishers, Boston 1997, ISBN 0-7923-9892-0
• Carroll, J., Long, D., Finite Automata 이론과 형식언어 도입프렌티스 홀, 엥글우드 클리프스, 1989.
• Kohavi, Z., 스위칭과 유한 오토마타 이론맥그로힐, 1978년
• Gill, A., 유한 상태 기계 이론 소개맥그로힐, 1962년
• 긴즈버그, S., 수학기계론 개론애디슨 웨슬리, 1962.

유한 상태 기계(오토마타 이론) 이론 컴퓨터 과학

• Arbib, Michael A. (1969). Theories of Abstract Automata (1st ed.). Englewood Cliffs, N.J.: Prentice-Hall, Inc. ISBN 978-0-13-913368-8.
• Bobrow, Leonard S.; Arbib, Michael A. (1974). Discrete Mathematics: Applied Algebra for Computer and Information Science (1st ed.). Philadelphia: W. B. Saunders Company, Inc. ISBN 978-0-7216-1768-8.
• Booth, Taylor L. (1967). Sequential Machines and Automata Theory (1st ed.). New York: John Wiley and Sons, Inc. Library of Congress Card Catalog Number 67-25924.
• Boolos, George; Jeffrey, Richard (1999) [1989]. Computability and Logic (3rd ed.). Cambridge, England: Cambridge University Press. ISBN 978-0-521-20402-6.
• Brookshear, J. Glenn (1989). Theory of Computation: Formal Languages, Automata, and Complexity. Redwood City, California: Benjamin/Cummings Publish Company, Inc. ISBN 978-0-8053-0143-4.
• Davis, Martin; Sigal, Ron; Weyuker, Elaine J. (1994). Computability, Complexity, and Languages and Logic: Fundamentals of Theoretical Computer Science (2nd ed.). San Diego: Academic Press, Harcourt, Brace & Company. ISBN 978-0-12-206382-4.
• Hopcroft, John; Ullman, Jeffrey (1979). Introduction to Automata Theory, Languages, and Computation (1st ed.). Reading Mass: Addison-Wesley. ISBN 978-0-201-02988-8.
• Hopcroft, John E.; Motwani, Rajeev; Ullman, Jeffrey D. (2001). Introduction to Automata Theory, Languages, and Computation (2nd ed.). Reading Mass: Addison-Wesley. ISBN 978-0-201-44124-6.
• Hopkin, David; Moss, Barbara (1976). Automata. New York: Elsevier North-Holland. ISBN 978-0-444-00249-5.
• Kozen, Dexter C. (1997). Automata and Computability (1st ed.). New York: Springer-Verlag. ISBN 978-0-387-94907-9.
• Lewis, Harry R.; Papadimitriou, Christos H. (1998). Elements of the Theory of Computation (2nd ed.). Upper Saddle River, New Jersey: Prentice-Hall. ISBN 978-0-13-262478-7.
• Linz, Peter (2006). Formal Languages and Automata (4th ed.). Sudbury, MA: Jones and Bartlett. ISBN 978-0-7637-3798-6.
• Minsky, Marvin (1967). Computation: Finite and Infinite Machines (1st ed.). New Jersey: Prentice-Hall.
• Papadimitriou, Christos (1993). Computational Complexity (1st ed.). Addison Wesley. ISBN 978-0-201-53082-7.
• Pippenger, Nicholas (1997). Theories of Computability (1st ed.). Cambridge, England: Cambridge University Press. ISBN 978-0-521-55380-3.
• Rodger, Susan; Finley, Thomas (2006). JFLAP: An Interactive Formal Languages and Automata Package (1st ed.). Sudbury, MA: Jones and Bartlett. ISBN 978-0-7637-3834-1.
• Sipser, Michael (2006). Introduction to the Theory of Computation (2nd ed.). Boston Mass: Thomson Course Technology. ISBN 978-0-534-95097-2.
• Wood, Derick (1987). Theory of Computation (1st ed.). New York: Harper & Row, Publishers, Inc. ISBN 978-0-06-047208-5.

추상적 상태 기계 이론 컴퓨터 과학

• Gurevich, Yuri (July 2000). "Sequential Abstract State Machines Capture Sequential Algorithms" (PDF). ACM Transactions on Computational Logic. 1 (1): 77–111. CiteSeerX 10.1.1.146.3017. doi:10.1145/343369.343384. S2CID 2031696.

유한 상태 알고리즘을 이용한 기계학습

• Mitchell, Tom M. (1997). Machine Learning (1st ed.). New York: WCB/McGraw-Hill Corporation. ISBN 978-0-07-042807-2.

하드웨어 공학 : 상태 최소화 및 순차회로 합성

• Booth, Taylor L. (1967). Sequential Machines and Automata Theory (1st ed.). New York: John Wiley and Sons, Inc. Library of Congress Card Catalog Number 67-25924.
• Booth, Taylor L. (1971). Digital Networks and Computer Systems (1st ed.). New York: John Wiley and Sons, Inc. ISBN 978-0-471-08840-0.
• McCluskey, E. J. (1965). Introduction to the Theory of Switching Circuits (1st ed.). New York: McGraw-Hill Book Company, Inc. Library of Congress Card Catalog Number 65-17394.
• Hill, Fredrick J.; Peterson, Gerald R. (1965). Introduction to the Theory of Switching Circuits (1st ed.). New York: McGraw-Hill Book Company. Library of Congress Card Catalog Number 65-17394.

유한 마르코프 연쇄 과정

"우리는 마르코프 체인이 일련의 상태를₁ 통해₂ 연속적으로_r 이동하는 과정이라고 생각할 수 있습니다. s, s. 상태에_i 있으면 p 확률의_ij 상태로_j 다음 단계로 이동합니다.이러한 확률은 전이 행렬의 형태로 나타낼 수 있습니다"(Kemeny(1959), 페이지 384).

유한 마르코프 체인 프로세스는 유한 유형의 서브쉬프트라고도 합니다.

• Booth, Taylor L. (1967). Sequential Machines and Automata Theory (1st ed.). New York: John Wiley and Sons, Inc. Library of Congress Card Catalog Number 67-25924.
• Kemeny, John G.; Mirkil, Hazleton; Snell, J. Laurie; Thompson, Gerald L. (1959). Finite Mathematical Structures (1st ed.). Englewood Cliffs, N.J.: Prentice-Hall, Inc. Library of Congress Card Catalog Number 59-12841. 6장 "무한 마코프 체인".

외부 링크

• 컬리의 유한 상태 오토마타
• 유한 상태 기계를 이용한 단순 인공지능 동작 모델링 비디오 게임에서의 사용 예시
• 유한 상태 기계의 자유 온라인 전산 사전 설명
• NIST 유한 상태 기계의 알고리즘 및 데이터 구조 사전 설명
• Mealy, Moore, Harrel 및 UML 상태 기계의 이론적 측면을 비교하는 상태 기계 유형에 대한 간략한 개요.