폭 우선 검색

폭 우선 검색
	노드가 확장되는 순서
학급	검색 알고리즘
data 구조	그래프
최악의 경우 성능
최악의 경우 공간의 복잡성

폭 우선 검색의 애니메이션 예제입니다.검정: 탐색 완료, 회색: 나중에 탐색하기 위해 대기열에 있음

메이즈 해결 알고리즘에서의 BFS

Tic-tac-toe 게임 트리 상단

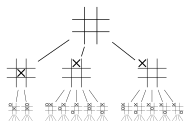
폭 우선 검색(BFS)은 주어진 속성을 충족하는 노드의 트리 데이터 구조를 검색하는 알고리즘입니다.트리 루트에서 시작하여 현재 깊이의 모든 노드를 탐색한 후 다음 깊이 수준에서 노드로 이동합니다.발견되었지만 아직 탐색되지 않은 하위 노드를 추적하려면 추가 메모리(일반적으로 큐)가 필요합니다.

예를 들어 체스 엔드게임에서 체스 엔진은 가능한 모든 동작을 적용하여 현재 위치에서 게임 트리를 구축하고 폭 우선 검색을 사용하여 흰색의 우승 위치를 찾을 수 있다.암묵적인 트리(게임 트리 또는 기타 문제 해결 트리 등)의 크기는 무한할 수 있습니다. 솔루션 노드가^[1] 존재할 경우 폭 우선 검색이 보장됩니다.

반면 (일반) 깊이 우선 검색은 다른 노드를 ^[2]역추적 및 확장하기 전에 노드 브랜치를 최대한 탐색하여 무한 브랜치로 손실되어 솔루션 노드에 도달하지 못할 수 있습니다.깊이 우선 검색을 반복하면 트리의 꼭대기를 반복해서 탐색하는 대가를 치르고 후자의 결점을 피할 수 있습니다.한편, 두 가지 깊이 우선 알고리즘 모두 추가 메모리 없이도 잘 작동합니다.

폭 우선 검색은 시작 노드(때로는 '^[3]검색 키'라고도 함)가 명시적으로 주어지고 정점을 두 번 따르는 것에 대한 예방 조치를 취할 때 그래프로 일반화할 수 있습니다.

BFS와 그래프의 연결된 구성요소를 찾기 위한 응용은 1945년 Konrad Zuse가 Plankalkül 프로그래밍 언어에 대한 박사 학위 논문에서 발명했지만,^[4] 이것은 1972년까지 발표되지 않았다.그것은 1959년 에드워드 F에 의해 재창조되었다. Moore는 미로에서 ^[5]^[6]최단 경로를 찾기 위해 이것을 사용했으며, 나중에 C. Y. 리에 의해 와이어 라우팅 알고리즘으로 개발되었습니다(1961년 ^[7]출판).

유사 코드

입력: $그래프$ G와 G의 $시작$ $정점근$

출력: 목표 상태.부모 링크는 $루트$ 까지의^[8] 최단 경로를 추적합니다.

1 프로시저 BFS(G, root)는 2로 Q를 4 Q.enqueue(root) 5로 큐3 라벨 루트로 하고 Q가 비어 있지 않은 경우 6 v:= Q.dequeue() 7을 실행하며 v가 목표인 경우 8은 v에서 w까지의 모든 에지에 대해 v 9를 반환합니다.adjacentEdges(v)는 11로 검색되지 않은 경우 10 w를 수행합니다.라벨 w는 12 Q.enqueue(w)로 조사됩니다.

상세

이 비재귀적 구현은 깊이 우선 검색의 비재귀적 구현과 유사하지만 다음과 같은 두 가지 점에서 다릅니다.

스택 대신 큐(First In First Out)를 사용합니다.
정점이 큐에서 큐잉 해제될 때까지 이 검사를 지연시키는 대신 정점을 큐잉하기 전에 탐색했는지 여부를 확인합니다.

G가 트리인 $경우$ 이 폭 우선 검색 알고리즘의 큐를 스택으로 대체하면 깊이 우선 검색 알고리즘이 생성됩니다.일반 그래프의 경우 반복 깊이 우선 검색 구현의 스택을 대기열로 대체하면 너비 우선 검색 알고리즘이 생성되지만 다소 비표준적입니다.^[9]

Q 큐에는 알고리즘이 현재 검색 중인 프런티어가 포함됩니다.

노드에는 실장에 따라 세트에 저장하거나 각 노드의 속성을 사용하여 탐색된 것으로 라벨을 붙일 수 있습니다.

단어 노드는 보통 단어 정점과 호환됩니다.

각 노드의 부모 어트리뷰트는, 예를 들면, BFS 가 실행되어 이전 노드의 설정이 끝난 후, 행선지 노드에서 기동 노드로의 백트래킹에 의해서 최단 패스로의 노드에 액세스 하는 경우에 편리합니다.

너비 우선 검색은 이른바 너비 우선 트리를 생성합니다.다음 예에서 너비 첫 번째 트리의 모양을 볼 수 있습니다.

예

다음은 프랑크푸르트에서 시작하는 독일 도시에서 BFS를 실행하여 얻은 너비 우선 트리의 예입니다.

도시 간 연결이 있는 남부 독일의 지도 예

지정된 지도에서 BFS를 실행하고 프랑크푸르트에서 시작할 때 얻은 너비 우선 트리

분석.

시간과 공간의 복잡성

모든 정점과 모든 $O(|V|+|E|)$ 가 $O(|V|+|E|)$ 의 $O(|V|+|E|)$ 경우 $O(|V|+|E|)$ 탐색되기 때문에 시간 $복잡도$ 는 O ( V + E ) {displaystyle O ( V + $E$ ) $O(|V|+|E|)$ 로 $O(|V|+|E|)$ 할 수 있습니다. $displaystyle$ V $)$ 는 $|V|$ 정점 수이고 $|E|$ E(\ $displaystyle$ E $)$ 는 $|E|$ 그래프에서 모서리 수입니다. $O(|E|)$ ( $O(|E|)$ ) { $display style$ O ( $E$ ) }는 $O(|E|)$ 입력 그래프의 ^[10]빈도에 따라 $O(1)$ O ( $O(1)$ ) { $display style$ O ( $1)$ $O(|V|^{2})$ ( $O(|V|^{2})$ 2 ) $O(|V|^{2})$ （ \ $displaystyle$ O ( V $^$ {2} ) $O(|V|^{2})$ 。

그래프의 꼭지점 수를 미리 알고 있고 큐에 이미 추가된 꼭지점을 확인하기 위해 추가 데이터 구조를 사용하는 경우 공간의 $O(|V|)$ 는 O $O(|V|)$ ( $O(|V|)$ ) \ $display style$ O ( $V$ ) $O(|V|)$ 。 $|V|$ 서 $|V|$ V { $display style$ V $|V|$ }는 $|V|$ 꼭지점 수입니다.이는 그래프 자체에 필요한 공간에 더하여 알고리즘 구현에 사용되는 그래프 표현에 따라 달라질 수 있습니다.

때도 명시적으로(또는 무한한)저장할 수 있을 만큼 크다 그래프와 함께 일하면서, 더 다른 개념에서:거리 d에 시작 노드(가장자리 traversals에서 측정)가 노드를 찾을breadth-first 검색의 복잡성을 묘사하는 것은 실제적입니다, BFS이의 b는"분기 계수"O(bd+1)시간과 기억이 걸린다.graph(평균 외도).^[11]^{: 81}

완전성

알고리즘 분석에서 폭 우선 탐색에 대한 입력은 인접 리스트, 인접 매트릭스 또는 유사한 표현으로 표현되는 유한 그래프라고 가정한다.그러나 인공지능에서 그래프 통과 방법의 적용에서 입력은 무한 그래프의 암묵적인 표현일 수 있다.이 문맥에서 검색방법은 목표상태가 존재하는 경우 반드시 목표상태를 찾을 수 있는 경우 완전한 것으로 설명된다.폭 우선 검색이 완료되었지만 깊이 우선 검색은 완료되지 않았습니다.암묵적으로 표현된 무한 그래프에 적용하면 폭 우선 검색은 결국 목표 상태를 찾지만 깊이 우선 검색은 목표 상태가 없는 그래프의 일부에서 손실되어 ^[12]반환되지 않을 수 있습니다.

BFS 주문

그래프의 꼭지점 열거는 BFS가 이 그래프에 적용 가능한 출력일 경우 BFS 순서라고 한다.

G $=$ ( $G=(V,E)$ , $G=(V,E)$ ) {\ $displaystyle$ G=( $V, E)}$ 을 $G=(V,E)$ $n$ $($ 를 $) n개$ 의 정점이 $있는$ 그래프라고 $G=(V,E)$ . $N(v)$ ) { $displaystyle$ N $(v)}$ 은 $N(v)$ v { $displaystyle$ v $v$ 의 네이버 집합입니다. = ( $\sigma =(v_{1},\dots ,v_{m})$ , $\sigma =(v_{1},\dots ,v_{m})$ , $\sigma =(v_{1},\dots ,v_{m})$ v $\sigma =(v_{1},\dots ,v_{m})$ m ) { $displaystyle$ \ $displaystyle =$ ( $v _$ {1} , \ $\sigma =(v_{1},\dots ,v_{m})$ $displaystyle$ , $v$ _ { $m$ $V$ )는 $\sigma =(v_{1},\dots ,v_{m})$ V { $v\in V\setminus \{v_{1},\dots ,v_{m}\}$ 1 $v\in V\setminus \{v_{1},\dots ,v_{m}\}$ 의 $v\in V\setminus \{v_{1},\dots ,v_{m}\}$ 요소 목록입니다 $v\in V\setminus \{v_{1},\dots ,v_{m}\}$ $m$ $v_{i}$ $\nu _{\sigma }(v)$ $displaystyle v_{i}$ 가 $v_{i}$ $v$ 의 $v$ 가 $v_{i}$ $\nu _{\sigma }(v)$ $(v$ $)$ 로 $\nu _{\sigma }(v)$ $i$ 하고 $,$ 그렇지 않으면 $vi$ \ $displaystyle$ $\infty$ v_{i $v$ 가 $\infty$ v $\displaystyle$ v의 네이버가 되도록 합니다 $.$

$\sigma =(v_{1},\dots ,v_{n})$ $\sigma =(v_{1},\dots ,v_{n})$ ( $\sigma =(v_{1},\dots ,v_{n})$ 1, $\sigma =(v_{1},\dots ,v_{n})$ , v $\sigma =(v_{1},\dots ,v_{n})$ ) $\sigma =(v_{1},\dots ,v_{n})$ { $displaystyle$ \ $displaystyle$ = ( v _ ${$ 1 $}$ , \ $\sigma =(v_{1},\dots ,v_{n})$ $displaystyle$ , $v$ _ { $n$ } $V$ } be $\sigma =(v_{1},\dots ,v_{n})$ an、 V $の$ of of of erationerationerationerationerationerationeration erationerationerationerationerationerationerationerationeration 。열거형 σ{\displaystyle \sigma}은 꼭지점 w∈ V∖{v1,…, vi1−}{\displaystyle w\in V\setminus){v_{1},\dots ,v_{i-1}\}가 되BFS 주문( 넣어 소스 v1{\displaystyle v_{1}})만약 모든 1개체,;in{\displaystyle 1<,i\leq n}≤, 나는}{\displaystyle v_{나는}v}s다고 한다uch지 $\nu _{(v_{1},\dots ,v_{i-1})}(w)$ $\nu _{(v_{1},\dots ,v_{i-1})}(w)$ ( $\nu _{(v_{1},\dots ,v_{i-1})}(w)$ $\nu _{(v_{1},\dots ,v_{i-1})}(w)$ , $\nu _{(v_{1},\dots ,v_{i-1})}(w)$ , $\nu _{(v_{1},\dots ,v_{i-1})}(w)$ i $\nu _{(v_{1},\dots ,v_{i-1})}(w)$ - 1 $\nu _{(v_{1},\dots ,v_{i-1})}(w)$ ) ( $\nu _{(v_{1},\dots ,v_{i-1})}(w)$ w ) { $displaystyle$ \ $nu$ _ { ( $v$ _ {1} , \ $displaystyle$ , $v$ _ { i - $\nu _{(v_{1},\dots ,v_{i-1})}(w)$ } } ( $w$ )는 $\nu _{(v_{1},\dots ,v_{i-1})}(w)$ 최소입니다.만약 내 < 모두 1≤,;j<>Equivalently,σ{\displaystyle \sigma}은 BFS, v와 k≤ n{\displaystyle 1\leq i<, j<,k\leq n}나는}N(vkm그리고 4.9초 만)∖ N(vj){\displaystyle v_{나는}\in N(v_{k})\setminus N(v_{j})∈를 주문하고,v j{\displaystyle의 이웃'v'm{\displaystyle v_{m}}존재한다.v_{j}}such $m<i$ < $m<i$ \ $display style m <$ i $m<i$

적용들

너비 우선 검색을 사용하여 그래프 이론의 많은 문제를 해결할 수 있습니다. 예를 들어 다음과 같습니다.

가비지 컬렉션 복사, 체니의 알고리즘
에지 수로 측정된 경로 길이를 사용하여 두 노드 u와 v 사이의 최단 경로 찾기(깊이 우선 ^[13]검색보다 이점)
(후진) Cuthill-McKee 메시 번호부여부
흐름 네트워크의 최대 흐름을 계산하는 Ford-Fulkerson 방법
바이너리 트리의 시리얼화/디시리얼화 vs 시리얼화를 정렬된 순서로 실시하면 트리를 효율적으로 재구성할 수 있습니다.
Aho-Corasick 패턴 매처 고장 함수 구축
그래프의 초당성을 테스트합니다.
그래프의 전이적 닫힘을 계산하기 위한 병렬 알고리즘 구현.^[14]

「」를 참조해 주세요.

레퍼런스

^ 즉, 지정된 속성을 충족하는 노드입니다.
^ Cormen Thomas H.; et al. (2009). "22.3". Introduction to Algorithms. MIT Press.
^ "Graph500 benchmark specification (supercomputer performance evaluation)". Graph500.org, 2010. Archived from the original on 2015-03-26. Retrieved 2015-03-15.
^ Zuse, Konrad (1972), Der Plankalkül (in German), Konrad Zuse Internet Archive. 링크된 pdf 파일의 96–105 페이지 (내부 번호 2.47–2.56)를 참조하십시오.
^ Moore, Edward F. (1959). "The shortest path through a maze". Proceedings of the International Symposium on the Theory of Switching. Harvard University Press. pp. 285–292. Cormen, Leiserson, Rivest 및 Stein이 인용한 바와 같이.
^ Skiena, Steven (2008). "Sorting and Searching". The Algorithm Design Manual. Springer. p. 480. Bibcode:2008adm..book.....S. doi:10.1007/978-1-84800-070-4_4. ISBN 978-1-84800-069-8.
^ Lee, C. Y. (1961). "An Algorithm for Path Connections and Its Applications". IRE Transactions on Electronic Computers. doi:10.1109/TEC.1961.5219222.
^ Cormen, Thomas H. "22.2 Breadth-first search". Introduction to algorithms. ISBN 978-81-203-4007-7. OCLC 1006880283.
^ "Stack-based graph traversal ≠ depth first search". 11011110.github.io. Retrieved 2020-06-10.
^ Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001) [1990]. "22.2 Breadth-first search". Introduction to Algorithms (2nd ed.). MIT Press and McGraw-Hill. pp. 531–539. ISBN 0-262-03293-7.
^ Russell, Stuart; Norvig, Peter (2003) [1995]. Artificial Intelligence: A Modern Approach (2nd ed.). Prentice Hall. ISBN 978-0137903955.
^ 코핀, B. (2004)인공지능이 켜졌다.Jones & Bartlett Learning, 페이지 79-80.
^ Aziz, Adnan; Prakash, Amit (2010). "4. Algorithms on Graphs". Algorithms for Interviews. p. 144. ISBN 978-1453792995.
^ Dhulipala, Laxman; Blelloch, Guy E.; Shun, Julian (August 21, 2019). Theoretically Efficient Parallel Graph Algorithms Can Be Fast and Scalable. p. 17. arXiv:1805.05208. doi:10.1145/3210377.3210414. ISBN 9781450357999. S2CID 44126609.

Knuth, Donald E. (1997), The Art of Computer Programming Vol 1. 3rd ed., Boston: Addison-Wesley, ISBN 978-0-201-89683-1

외부 링크

오픈 데이터 구조 - 섹션 12.3.1 - 폭 우선 검색, Pat Morin

[1] 즉, 지정된 속성을 충족하는 노드입니다.

[2] Cormen Thomas H.; et al. (2009). "22.3". Introduction to Algorithms. MIT Press.

[3] "Graph500 benchmark specification (supercomputer performance evaluation)". Graph500.org, 2010. Archived from the original on 2015-03-26. Retrieved 2015-03-15.

[:0-4] Zuse, Konrad (1972), Der Plankalkül (in German), Konrad Zuse Internet Archive. 링크된 pdf 파일의 96–105 페이지 (내부 번호 2.47–2.56)를 참조하십시오.

[5] Moore, Edward F. (1959). "The shortest path through a maze". Proceedings of the International Symposium on the Theory of Switching. Harvard University Press. pp. 285–292. Cormen, Leiserson, Rivest 및 Stein이 인용한 바와 같이.

[skiena-6] Skiena, Steven (2008). "Sorting and Searching". The Algorithm Design Manual. Springer. p. 480. Bibcode:2008adm..book.....S. doi:10.1007/978-1-84800-070-4_4. ISBN 978-1-84800-069-8.

[7] Lee, C. Y. (1961). "An Algorithm for Path Connections and Its Applications". IRE Transactions on Electronic Computers. doi:10.1109/TEC.1961.5219222.

[8] Cormen, Thomas H. "22.2 Breadth-first search". Introduction to algorithms. ISBN 978-81-203-4007-7. OCLC 1006880283.

[9] "Stack-based graph traversal ≠ depth first search". 11011110.github.io. Retrieved 2020-06-10.

[clrs-10] Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001) [1990]. "22.2 Breadth-first search". Introduction to Algorithms (2nd ed.). MIT Press and McGraw-Hill. pp. 531–539. ISBN 0-262-03293-7.

[11] Russell, Stuart; Norvig, Peter (2003) [1995]. Artificial Intelligence: A Modern Approach (2nd ed.). Prentice Hall. ISBN 978-0137903955.

[coppin-12] 코핀, B. (2004)인공지능이 켜졌다.Jones & Bartlett Learning, 페이지 79-80.

[13] Aziz, Adnan; Prakash, Amit (2010). "4. Algorithms on Graphs". Algorithms for Interviews. p. 144. ISBN 978-1453792995.

[14] Dhulipala, Laxman; Blelloch, Guy E.; Shun, Julian (August 21, 2019). Theoretically Efficient Parallel Graph Algorithms Can Be Fast and Scalable. p. 17. arXiv:1805.05208. doi:10.1145/3210377.3210414. ISBN 9781450357999. S2CID 44126609.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

v t 데이터 구조 및 알고리즘
데이터 구조	어레이 연관 배열 이진 검색 트리 펜윅나무 그래프 해시 테이블 히프 링크 리스트 큐 세그먼트 트리 스택 스트링 트리 트리
알고리즘	역추적 바이너리 검색 폭 우선 검색 깊이 우선 검색 분열시켜 정복하다. 동적 프로그래밍 접다 욕심쟁이 미니맥스 재귀 정렬 스트리밍 스위프 라인 토폴로지 정렬
데이터 구조 목록 알고리즘 목록

Search

폭 우선 검색

네임스페이스

더

목차

유사 코드

상세

예

분석.

시간과 공간의 복잡성

완전성

BFS 주문

적용들

「」를 참조해 주세요.

레퍼런스

외부 링크

Search

폭 우선 검색

유사 코드

상세

예

분석.

시간과 공간의 복잡성

완전성

BFS 주문

적용들

「 」를 참조해 주세요.

레퍼런스

외부 링크

「」를 참조해 주세요.