추체함수

함수
x ↦ f (x)
도메인 및 코도메인의 예
$(\displaystyle X}$ → ${\displaystyle \mathbb{B}}$ ${\$ $\},$ $\displaystyle \mathb {B} }$ → ${\displaystyle X}$ ${\displaystyle$ X$\},$ ${\displaystyle \mathb{B} ^{n}}$ → $(\displaystyle X}$ $(\displaystyle X}$ → ${\displaystyle \mathbb{Z}}$ ${\$ $\displaystyle \mathb {Z} }$ → $(\displaystyle X}$ $(\displaystyle X}$ → ${\displaystyle \mathbb{R}}$ ${\$ $\},$ ${\displaystyle \mathb {R} }$ → ${\displaystyle X}$ ${\displaystyle$ X$\},$ ${\displaystyle \mathb{R} ^{n}}$ → $(\displaystyle X}$ $(\displaystyle X}$ → ${\displaystyle \mathbb{C}}$ ${\$ ${\displaystyle \mathb {C} }$ → ${\displaystyle X}$ ${\displaystyle$ X$\},$ ${\displaystyle \mathb{C} ^{n}}$ → $(\displaystyle X}$
클래스/속성
상수 아이덴티티 선형 다항식 이성적 대수학 분석적 부드러움 연속 측정 가능 주입식 굴욕적인 비주사적
시공
제한 구성 λ 반비례
일반화
부분적 다중값 암묵적
v t

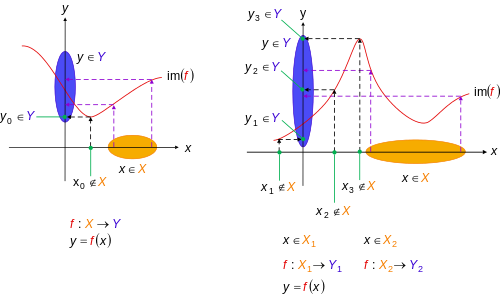
수학에서 굴절 함수(설사 또는 함수 위로도 알려져 있음)는 원소 x를 모든 원소 y에 매핑하는 함수 f이다. 즉, 모든 y에 대해 f(x) = y와 같은 x가 있다. 즉, 함수 코도메인의 모든 원소는 그 영역의 적어도 한 원소의 이미지다.^[1][2] x가 고유할 필요는 없다. 함수 f는 하나 이상의 X 요소를 Y의 동일한 요소에 매핑할 수 있다.

이 가명으로 1935년부터 현대 고급 수학의 전시를 제시하는 시리즈 책을 쓴 프랑스 20세기 수학자들의 모임인 ^[3][4]니콜라스 부르바키에 의해 '굴욕적'이라는 용어와 관련 용어들이 소개되었다. 프랑스어 sur는 오버나 그 이상을 의미하며, 굴절함수의 영역 이미지가 함수의 코도메인을 완전히 덮는다는 사실과 관련된다.

어떤 기능도 그것의 코도메인을 그것의 도메인의 이미지로 제한함으로써 추론을 유도한다. 모든 굴절함수는 오른쪽 역수를 가지고 있고, 오른쪽 역수를 가진 모든 함수는 반드시 추론이다. 처절함수의 구성은 언제나 처절하다. 어떤 기능도 투약과 주입으로 분해될 수 있다.

정의

허탈함수는 이미지가 코도메인과 동일한 함수를 말한다. $마찬가지$로, $Y{\displaystyle }$ ${\displaystyle X$$}$ 도메인과$$$$ Y$${\$displaystyle$ $Y}$ $코도메인{\displaystyle }$ $Y{\displaystyle }$ ${\displaystyle$ $Y$$}$이(가) 있는$$$$ $모든{\displaystyle }$ $y{\displaystyle }$ {\displaystyle Y$}$에 ${\displaystyle \mathrm{대해}}$ f${\displaystyle (x)}$= ${\displaystystyle x$$}$이($가)$ 하나 이상 존재하면$$ percuffective이다.$y$^[1] 거부는 $때때로{\displaystyle }$ f${\displaystyle }$: ${\displaystyle X}$ ${\displaystyle \twoheadrightarrow }$ ${\displaystyle Y}$ ${\displaystyle f\colon X\twohead rightarrow$ Y$}$에서와 같이 두 개의 머리 오른쪽 화살표(U+21A0 ↠ RIGHWARDS TWORD TWORKED ARROW)^[5]로 표시된다$.$

상징적으로

$f{\displaystyle }$: ${\displaystyle X}$→ ${\displaystyle Y}$ ${\displaystyle f\colon X\rightarrow Y}$인 경우$,$$$f {\displaystyle f$}$은(는) 다음인 경우, $다음$인 경우, p {\$displaystyle$ f}은(는) 굴절적이라고 한다$$.

${\displaystyle \mathrm{\forall }}$ ${\displaystyle y}$ ,${\displaystyle \exists \mathrm{}}$ ${\displaystyle x}$ ${\displaystyle \in }$ ${\displaystyle X}$, f${\displaystyle }$( ${\displaystyle x}$)${\displaystyle }$= ${\displaystyle y}$ ${\\displaystyle$\$forall y\in Y,\,\exists x\in X,\;f(x)=y}$^[2][6].

예

• 설정된 X에 대해 X의 ID 함수 ID는_X 추연적이다.
• f(n) = n mod 2로 정의된 f : Z → {0, 1} 함수(즉, 짝수 정수도 0으로 매핑되고 홀수 정수도 1로 매핑됨)는 굴절적이다.
• f(x) = 2x + 1로 정의한 함수 f : R → R은 굴절적이다(그리고 심지어 비굴절적이다). 왜냐하면 우리는 모든 실제 숫자 y에 대해 f(x) = y: 그러한 적절한 x는 (y - 1)/2이다.
• f(x) = x³ - 3x로 정의한 함수 f : R → R = x - 3x는 임의의 실수 y의 사전 이미지가 입방 다항 방정식³ x - 3x - y = 0의 솔루션 집합이고, 실제 계수를 가진 모든 입방 다항식은 최소 하나의 실제 루트를 가지기 때문에 굴절적이다. 그러나, 예를 들어, y = 2의 사전 이미지가 {x = -1, x = 2}이기 때문에, 이 함수는 주입되지 않는다(그러므로, 이 함수의 사전 이미지는 모든 y, -2 ≤ y ≤ 2에 대해 둘 이상의 요소가 있다).
• g²(x) = x에² 의해 정의된 함수 g : R → R은 x = -1과 같은 실제 숫자 x가 없기 때문에 굴절적이지 않다. 단, g(x) = x²(제한된 코도메인 포함)로 정의한 함수 g : R → R은_≥0 부차적인데, 비음성의 실제 코도메인 Y의 모든 y에 대해 실제 영역 X에는 x² = y와 같은 x가 적어도 하나 이상 존재하기 때문이다.
• 자연 로그 함수 ln : (0, +biques) → R은 (양수 실수의 집합에서 모든 실수의 집합으로 매핑) 굴절적이고 짝수 이심적인 것이다. 그것의 역수인 지수함수는, 실수의 집합을 도메인으로 정의한다면, (그 범위는 양의 실수의 집합이기 때문에) 허탈하지 않다.
• 매트릭스 지수라는 것은 모든 n×n 매트릭스의 공간으로부터 그 자체로 지도로 볼 때 추월적이지 않다. 그러나, 일반적으로 모든 n×n 행렬의 공간으로부터 일반적인 n×n도 선형 그룹(즉, 모든 n×n 반전성 행렬의 그룹)에 이르는 지도로 정의된다. 이 정의에 따르면 매트릭스 지수(matrix indexial)는 실제 매트릭스에 대해서는 여전히 굴절적이지 않지만 복잡한 매트릭스에 대해서는 굴절적이다.
• 데카르트 제품 A × B에서 그 요인 중 하나에 대한 투영법은 다른 요인이 비어 있지 않는 한 절망적이다.
• 3D 비디오 게임에서 벡터는 허탈적 기능을 통해 2D 평면 스크린에 투영된다.

특성.

함수는 그것이 굴절적이거나 주입적이거나 둘 다인 경우에만 비굴적이다.

(흔히 행해지는 대로) 함수가 그 그래프로 식별되는 경우, 허탈성은 함수 자체의 속성이 아니라 매핑의 속성이 된다.^[7] 이것은 코도메인과 함께 함수를 말한다. 주입도와는 달리 함수의 그래프에서만 허탈성을 읽을 수 없다.

우측 되돌릴 수 없는 함수로써 거부

함수 g : Y → X는 함수 f : X → Y의 모든 y에 대해 f(g(y) = y(g는 f로 실행 취소할 수 있음)의 역행이라고 한다. 즉, g의 구성 f o g와 f가 g의 도메인 Y에 있는 ID 함수라면 g는 f의 오른쪽 역순이다. 함수 g는 f의 도메인 X에서 다른 순서인 go f의 구성이 ID 함수가 아닐 수 있기 때문에 f의 완전한 역순일 필요는 없다. 즉 f는 되돌리거나 "역행" g를 할 수 있지만 반드시 그것에 의해 역전될 수는 없다.

모든 함수의 역행은 필연적으로 추론이다. 모든 허탈함수가 올바른 역수를 가지고 있다는 명제는 선택의 공리와 동등하다.

f : X → Y가 허탈적이고 B가 Y의 부분집합이라면 f(f ⁻¹(B) = B. 따라서 B는 그 프리이미지 f ⁻¹(B)에서 회복될 수 있다.

예를 들어 위의 첫 번째 그림에는 g(C) = 4와 같은 함수 g가 있다. f(4) = C와 같은 기능도 있다. g(C)도 3과 같을 수 있다는 것은 중요하지 않다. 단지 f가 "역전"하는 것만이 중요하다.

• 

  허탈적 구성: 첫 번째 기능은 허탈할 필요가 없다.

• 

  또 다른 처절함수. (이것은 우연히 편견이다)

• 

  비주사 함수. (이것은 우연히 주사를 맞았다)

경구적 표현으로서의 거절

함수 f : X → Y는 우측 취소인 경우에만 ^[8]굴절적이다: 어떤 함수 g,h : Y → Z가 주어지면 go f = h o f, g = h. 이 특성은 기능 및 그 구성의 관점에서 공식화되며, 범주의 형태와 구성의 보다 일반적인 개념으로 일반화될 수 있다. 오른쪽 취소형 형태는 경구형이라고 불린다. 구체적으로는 추체함수는 정확히 집합의 범주에 있는 인식함수다. 접두사 epi는 그리스 전치사 ἐπί에서 따온 것이다.

올바른 역의 어떤 형태론도 인식론이지만, 그 역행은 일반적으로 사실이 아니다. 형태론 f의 오른쪽 역 g는 f의 한 섹션이라고 불린다. 오른쪽 역의 형태론을 분할 인식론이라고 한다.

이항 관계로서의 거절

도메인 X와 코도메인 Y를 가진 모든 함수는 함수 그래프로 그것을 식별함으로써 X와 Y 사이의 왼쪽 총 및 오른쪽 고유 이진 관계로 볼 수 있다. 도메인 X와 코도메인 Y를 가진 허탈 함수는 오른쪽 단일한 X와 Y 사이의 이진 관계가 되며 왼쪽 총계와 오른쪽 총계가 모두 된다.

추론 영역의 카디널리티

처절함수 영역의 카디널리티는 코도메인의 카디널리티보다 크거나 같다. f : X → Y가 굴절 함수라면, X는 적어도 추기경 숫자의 의미에서 Y만큼의 원소를 가지고 있다.(증거는 Y의 모든 Y에 대해 함수 g : Y → X를 만족시키는 f(g(y) = y가 존재한다는 것을 보여주는 선택 공리에 호소한다. g는 주입하는 것으로 쉽게 볼 수 있으므로, Y x X의 공식적 정의가 충족된다.)

구체적으로는 X와 Y가 모두 동일한 수의 원소를 가지고 유한한 경우, f : X → Y는 f가 주입적인 경우에만 추연적이다.

X와 Y의 두 세트가 주어졌을 때,^* X notation Y라는 표기법은 X가 비어 있거나 Y에서 X로 추론하는 데 사용된다. 선택 공리를 사용하면 X ≤^* Y와 Y ≤^* X가 함께 슈뢰더-베른슈타인 정리의 변종인 Y = X를 암시한다는 것을 알 수 있다.

구성 및 분해

허탈함수의 구성은 항상 허탈함수: f와 g가 모두 허탈함수이고, g의 코도메인이 f의 영역과 같다면 f o g는 허탈함수다. 반대로 f o g가 허탈적이라면 f는 허탈적(그러나 g, 먼저 적용된 함수, 그럴 필요는 없다)이다. 이러한 속성은 집합 범주의 거절에서 어떤 범주의 어떤 경시현상까지 일반화한다.

모든 기능은 투사 및 주입으로 분해될 수 있다. 모든 함수 h : X → Z에 대해 h = g o f와 같은 분사 f : X → Y, 그리고 주입 g : Y → Z가 존재한다. 이를 확인하려면 Y를 z가 h(X)에 있는 사전 이미지 집합으로⁻¹ 정의하십시오. 이 프리이미지들은 분리되어 있고 칸막이 X이다. 그런 다음 f는 각 x를 포함하는 Y의 요소로 운반하고, g는 각 y의 요소를 h가 점을 보내는 Z의 점으로 운반한다. 그러면 f는 투영지도이기 때문에 허탈하고, g는 정의에 의해 주입된다.

유도분사 및 유도분사

어떤 기능이라도 코도메인을 그 범위로 제한함으로써 추론을 유도한다. 어떤 처절함수는 주어진 고정된 이미지에 매핑되는 모든 인수를 접음으로써 그 영역의 지수에 정의된 편차를 유도한다. 더 정확히 말하면, 모든 투영 f : A → B는 다음과 같은 투영으로 간주될 수 있다. A/~는 다음과 같은 동등성 관계에서 A의 동등성 등급이 되도록 한다: f(x) = f(y)인 경우에만 x ~ y. 동등하게, A/~는 f 아래의 모든 사전 이미지의 집합이다. 렛츠 P(~) : A → A/~의 각 x를 등가 등급[x]_~으로 보내는 투영지도가 되고 f_P : A/~B는 f_P([x]_~ = f(x)가 주는 잘 정의된 함수다. 그러면 f = f_P o P(~)가 된다.

거절의 공간

A와 B가 고정되어 있으면 A ↠ B의 기각 집합을 형성할 수 있다. The cardinality of this set is one of the twelve aspects of Rota's Twelvefold way, and is given by ${\textstyle B !{\begin{Bmatrix} A \\ B \end{Bmatrix}}}$, where ${\textstyle {\begin{Bmatrix} A \\ B \end{Bmatrix}}}$ denotes a Stirling number of t그는 이류다.

참고 항목

위키미디아 커먼스는 추태와 관련된 미디어를 보유하고 있다.

허탈, 허탈, 혹은 무료 사전인 위키트리노에서 찾아보자.

• 바이어스, 주입 및 분사
• 커버(알지브라)
• 커버링 맵
• 열거
• 섬유다발
• 인덱스 세트
• 단면(범주 이론)

참조

추가 읽기

• Bourbaki, N. (2004) [1968]. Theory of Sets. Elements of Mathematics. 1. Springer. doi:10.1007/978-3-642-59309-3. ISBN 978-3-540-22525-6. LCCN 2004110815.