파티션(숫자 이론)

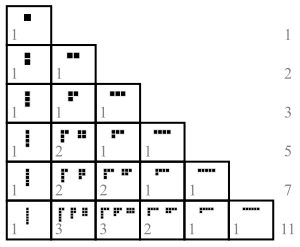
정수론과 조합론에서, 음이 아닌 정수 n의 파티션은 양의 정수의 합으로 n을 쓰는 방법입니다.합의 순서만 다른 두 합은 동일한 분할로 간주됩니다.(순서가 중요한 경우 합은 구성이 됩니다.)예를 들어 4는 다음과 같은 다섯 가지 방법으로 분할할 수 있습니다.

4

3 + 1

2 + 2

2 + 1 + 1

1 + 1 + 1 + 1

0의 유일한 분할은 부분이 없는 빈 합입니다.

순서에 의존하는 조성 1 + 3은 3 + 1과 같은 파티션이고, 두 개의 다른 조성 1 + 2 + 1과 1 + 1 + 2는 2 + 1 + 1과 같은 파티션입니다.

파티션의 개별 합을 부품이라고 합니다.n의 파티션 수는 파티션 함수 p(n)에 의해 주어집니다.소프(4) = 5.표기 ⊢ λ λ는 is가 n의 분할임을 의미합니다.

파티션은 영 다이어그램 또는 페러 다이어그램으로 그래픽으로 시각화할 수 있습니다.이들은 일반적으로 대칭 다항식과 대칭군 및 군 표현 이론의 연구를 포함한 수학 및 물리학의 여러 분야에서 발생합니다.

예

5의 7개의 칸막이는

• 5
• 4 + 1
• 3 + 2
• 3 + 1 + 1
• 2 + 2 + 1
• 2 + 1 + 1 + 1
• 1 + 1 + 1 + 1 + 1

일부 저자는 파티션을 더하기 기호가 있는 표현이 아니라 감소하는 요약 순서로 취급합니다.예를 들어, 파티션 2 + 2 + 1은 대신 튜플(2, 2, 1)로 쓰이거나 위첨자가 부품의 반복 횟수를 나타내는 훨씬 더 압축된 형태²(2, 1)로 쓸 수 있습니다.

파티션에 대한 이 다중도 표기는 ${\displaystyle 1^{}}$ m ${\displaystyle {1_{}}^{}}$ ${\displaystyle {{}_{}}^{}}$ ${\displaystyle {m_{}}^{}}$ ${\displaystyle {{}_{}}^{}}$ ${\displaystyle 3^{}}$ m ${\displaystyle {3_{}}^{}}$ ⋯ {\$displaystyle$ 1$^{m_{1}},$ 2$^{m_{2}},$ 3$^{m_{3}}\cdots$여기서 m은 1의 개수, m은 2의 개수 등)로 대체하여 쓸 수 있습니다. (m = 0인 성분은 생략할 수 있습니다.)예를 들어, 이 표기법에서 5의 파티션은 ${\displaystyle {5\mathrm{}}^{}}$ ${\displaystyle {\mathrm{}}^{}{}^{}}$1, ${\displaystyle {1\mathrm{}}^{}}$1 ${\displaystyle {\mathrm{}}^{}}$ ${\displaystyle {1\mathrm{}}^{}}$, ${\displaystyle {2\mathrm{}}^{}}$1 ${\displaystyle {}^{}{\mathrm{}}^{}}$ ${\displaystyle {\mathrm{}}^{}}$,${\displaystyle {}^{}{1\mathrm{}}^{}}$ ${\displaystyle {\mathrm{}}^{}}$ 3 ${\displaystyle {1\mathrm{}}^{}}$ ${\displaystyle {\mathrm{}}^{}}$ 2 2, 1 ${\displaystyle {}^{}{\mathrm{}}^{}}$ 2 ${\displaystyle {1\mathrm{}}^{}}$ ${\$ 5$^{1},$ 1$^{1}, 2^{1}3^{1}, 1^{2}3^{1},$ 1$^{2}, 1^{3}2^{1$ ${\displaystyle {15\mathrm{}}^{}}${\$displaystyle$ 1$^{5$로 $적습니다{\displaystyle {\mathrm{}}^{}}$.

파티션의 다이어그램 표현

파티션을 나타내는 두 가지 일반적인 다이어그램 방법은 Norman Macleod Ferrers의 이름을 딴 Ferrers 다이어그램과 Alfred Young의 이름을 딴 Young 다이어그램입니다.둘 다 몇 가지 가능한 규칙이 있습니다. 여기서는 왼쪽 상단에 도표가 정렬된 영어 표기법을 사용합니다.

페러스 도표

숫자 14의 파티션 6 + 4 + 3 + 1은 다음 다이어그램으로 나타낼 수 있습니다.

14개의 원은 4개의 행으로 정렬되어 있으며, 각 원은 파티션의 일부 크기입니다.숫자 4의 5개 파티션에 대한 다이어그램은 다음과 같습니다.

4	=	3 + 1	=	2 + 2	=	2 + 1 + 1	=	1 + 1 + 1 + 1

영도

정수 파티션의 대안적인 시각적 표현은 영 다이어그램(종종 페러 다이어그램)입니다.페러 다이어그램처럼 점으로 파티션을 표시하는 대신 영 다이어그램은 상자 또는 정사각형을 사용합니다.따라서 파티션 5 + 4 + 1에 대한 영 다이어그램은

동일한 파티션에 대한 페러 다이어그램은

영 다이어그램은 대칭 함수와 군 표현 이론의 연구에서 매우 유용한 것으로 밝혀졌습니다. 영 다이어그램의 상자를 숫자로 채우는 것은 다양한 규칙을 따르는 것은 윤이라고 불리는 대상의 패밀리로 이어집니다.gtableaux와 이 tableaux는 조합론적, 표현론적 의미를 ^[1]갖습니다.인접한 사각형들이 서로 결합하여 만든 형태로서, 영 다이어그램은 폴리오미노의 ^[2]특별한 종류입니다.

파티션 함수

파티션 $함수{\displaystyle }$p (${\displaystyle n}$ )$${\$displaystyle$ p$(n)}$은(는) 음이 아닌 $정수{\displaystyle }$ n$${\$displaystyle$ n$\}$의 파티션을 카운트합니다. 예를 들어${\displaystyle }$$정수{\displaystyle \mathrm{}}$ 4$$${\$$displaystyle$ 4$}$에는 $파티션{\displaystyle \mathrm{}}$1 +${\displaystyle 1}$ +${\displaystyle 1}$ + ${\displaystyle 1}$ ${\displaystyle$1 +$1$ + 1 + 1 + 1 +$$${\displaystyle 1}$$\},$${\displaystyle 1}$${\displaystyle }$+${\displaystyle }$${\displaystyle 3}${\$displaystyle$1 +$1$ + $2$ $2{\displaystyle \mathrm{}}$${\displaystyle }$+ 2$${\$displaystyle$1 + 3}, {\displaystyle 1 + $3$ 2 + ${\displaystyle 2}$ {\$displaystyle$ 1 + 3$}$이${\displaystyle (}$가) $있습니다$.$aystyle$ 2$+2$ $및{\displaystyle \mathrm{}}$ 4$${\$displaystyle$ 4$\}.$n = ${\displaystyle 0,}$ ${\displaystyle 1,}$ $2$… {\$displaystyle$ n =$0, 1,$ 2,\$display}$에 $대한$ 이 함수의 값은 다음과 같습니다.

1, 1, 2, 3, 5, 7, 11, 15, 22, 30, 42, 56, 77, 101, 135, 176, 231, 297, 385, 490, 627, 792, 1002, 1255, 1575, 1958, 2436, 3010, 3718, 4565, 5604, ...(OEIS의 서열 A000041).

p ${\displaystyle$ p$}$의 생성 함수는

${\displaystyle \sum _{n=0}^{\infty }p(n)q^{n}=\sum _{j=1}^{\infty }\sum _{i=0}^{\infty }q^{ji}=\sum _{j=1}^{\infty }(1-q^{j})^{-1}}$

분할 함수에 대한 닫힌 형식 표현은 알려져 있지 않지만, 정확하게 근사하는 점근적 확장과 정확하게 계산할 수 있는 반복 관계를 모두 가지고 있습니다.이는 다음과 같이 인수의 제곱근의 지수 함수로 성장합니다.^[3]

${\displaystyle p}$(${\displaystyle n}$) ~ ${\displaystyle \frac{\mathrm{14}}{}}$ n ${\displaystyle 3}$ ${\displaystyle e}$xp ${\displaystyle }$ ( ${\displaystyle \pi }$ 2 ${\displaystyle \sqrt{\frac{n}{}\frac{}{}}}$ )$${\$displaystyle$ p$(n$)\$sim${\$frac {1}{4n{\sqrt {3}}}\exp \l$ ({\$pi${\$sqrt${\$frac {2n}{3}}\right)}$를 ${\displaystyle n}$ ${\displaystyle \to }$ $∞$ {\$displaystyle$ n$\to \infty$}

생성 함수의 곱셈 역수는 오일러 함수입니다. 오일러의 오각수 정리에 의해 이 함수는 인수의 오각수 거듭제곱의 합입니다.

${\displaystyle p(n)=p(n-1)+p(n-1)-p(n-5)-p(n-7)+\cdots }$

스리니바사 라마누잔(Srinivasa Ramanujan)은 모듈러 산술에서 분할 함수가 중요하지 않은 패턴을 갖는다는 것을 발견했는데, 이를 라마누잔의 합이라고 합니다.예를 들어 n ${\displaystyle$ n$}$의 십진수 표현이 숫자 4 또는 9로 끝날 때마다 n$${\$displaystyle$ n$}$의 파티션 수를 ^[4]5로 분할할 수 있습니다.

제한된 파티션

조합론과 수론 모두에서 다양한 제한을 받는 파티션 계열이 자주 ^[5]연구됩니다.이 절에서는 몇 가지 제한 사항을 조사합니다.

컨쥬게이트 파티션 및 자체 컨쥬게이트 파티션

분할 6 + 4 + 3 + 1 의 도표를 주 대각선을 따라 뒤집으면 다음과 같은 14개의 분할을 얻을 수 있습니다.

	↔
6 + 4 + 3 + 1	=	4 + 3 + 3 + 2 + 1 + 1

행을 열로 만들어서 숫자 14의 파티션 4 + 3 + 3 + 2 + 1 + 1을 얻습니다.이러한 파티션은 서로 ^[6]공역이라고 합니다.숫자 4의 경우, 칸막이 4와 1+1+1+1+1은 켤레쌍이고, 칸막이 3+1과 2+1+1+1은 서로 켤레쌍입니다.특히 관심있는 것은 2 + 2와 같은 칸막이들인데, 이 칸막이들은 스스로 결합체로 존재합니다.이러한 파티션은 자가 ^[7]결합이라고 합니다.

청구항: 자체 결합 파티션의 개수는 홀수 부분이 뚜렷한 파티션의 개수와 동일합니다.

증명(개요):중요한 관찰은 모든 홀수 부분이 중간에 접혀져서 자기 결합 다이어그램을 형성할 수 있다는 것입니다.

↔

그러면 홀수 부분이 뚜렷한 파티션 집합과 자체 결합 파티션 집합 사이의 편사를 얻을 수 있습니다. 예를 들어 다음과 같습니다.

	↔
9 + 7 + 3	=	5 + 5 + 4 + 3 + 2
디스트 홀수		자숙의

홀수 부분과 구별되는 부분

숫자 8의 22개의 파티션 중 홀수 부분만을 포함하는 6개가 있습니다.

• 7 + 1
• 5 + 3
• 5 + 1 + 1 + 1
• 3 + 3 + 1 + 1
• 3 + 1 + 1 + 1 + 1 + 1
• 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1

또는 숫자가 두 번 이상 발생하지 않는 파티션을 셀 수 있습니다.이러한 파티션을 구분되는 부분이 있는 파티션이라고 합니다.서로 다른 부분이 있는 8의 파티션을 세어보면 다음과 같은 6을 얻을 수 있습니다.

• 8
• 7 + 1
• 6 + 2
• 5 + 3
• 5 + 2 + 1
• 4 + 3 + 1

이것은 일반적인 재산입니다.각 양수에 대해 홀수 부분이 있는 파티션의 수는 q(n)^[8][9]으로 표시되는 개별 부분이 있는 파티션의 수와 같습니다.이 결과는 1748년^[10] 레온하르트 오일러에 의해 증명되었고 후에 글라이셔 정리로 일반화되었습니다.

제한된 파티션의 모든 유형에 대해 지정된 제한을 만족하는 파티션 수에 해당하는 함수가 있습니다.중요한 예로는 q(n)(파티션을 구분되는 부분으로 구분)이 있습니다.q(n)의 처음 몇 개의 값은 (q(0)=1로 시작):

1, 1, 1, 2, 2, 3, 4, 5, 6, 8, 10, ... (OEIS의 시퀀스 A000009).

q(n)에 대한 생성 함수는 다음과^[11] 같습니다.

${\displaystyle \sum _{n=0}^{\infty }q(n)x^{n}=\displaystyle \sum _{k=1}^{\infty }(1+x^{k})=\displaystyle \sum _{k=1}^{\infty }{\frac {1-x^{2k-1}}}$

오각수 정리는 ^[12]q에 대한 반복을 제공합니다.

q(k) = a + q(k - 1) + q(k - 2) - q(k - 5) - q(k - 7) + q(k - 12) + q(k - 15) - ...

여기서 a는 어떤 정수 m에 대하여 k = 3m - m이면 (-1)이고, 그렇지 않으면 0입니다.

제한된 부품 크기 또는 부품 수

공액을 취함으로써 n의 파티션 수 p_k(n)는 가장 큰 부분이 k의 크기를 갖는 n의 파티션 수와 같습니다.함수_k p(n)이 재발을 만족합니다.

p(n) = p(n - k) + p(n - 1)

n ≤ 0 또는 k ≤ 0이고 n 및 k가 모두 0이 아닌 경우 초기값 p(0) = 1 및 p(n) = 0인 경우.

함수 p(n)을 다음과 같이 복구합니다.

${\displaystyle p(n)=\sum _{k=0}^{n}p_{k}(n).}$

k개의 고정 변수와 n개의 변수를 사용하여 이러한 파티션을 생성할 수 있는 하나의 가능한 함수는 다음과 같습니다.

${\displaystyle \sum _{n\geq 0}p_{k}(n)x^{n}=x^{k}\frac _{i=1}^{k}{\frac {1}{1-x^{i}}}$

보다 일반적으로, T가 양의 정수의 집합일 경우, 부분이 모두 T에 속하는 n의 분할 수는 생성 함수를 갖습니다.

${\displaystyle \prod _{t\in T}(1-x^{t})^{-1}}$

이것은 (집합 T가 사용 가능한 코인을 지정하는) 변경 문제를 해결하는 데 사용될 수 있습니다.두 가지 특정한 경우로서, 하나는 모든 부분이 1 또는 2인 n의 파티션 수(또는 동등하게 n을 1 또는 2 부분으로 분할하는 파티션 수)가 다음과 같습니다.

${\displaystyle \left\loor {\frac {n}{2}}+1\rfoor,}$

그리고 모든 부분이 1, 2 또는 3인 n의 파티션 수(또는 n에서 최대 세 부분으로 분할된 파티션의 수)는 (n + ²3) ^[14]/ 12에 가장 가까운 정수입니다.

직사각형의 파티션 및 가우스 이항 계수

부품의 개수와 크기를 동시에 제한할 수도 있습니다.p(N, M;n)를 최대 M개의 부품을 가진 n의 파티션 수, 각각의 크기는 최대 N개라고 하자. 이와 동일하게 이들은 영 다이어그램이 M × N 직사각형 안에 들어맞는 파티션들입니다.재발 관계가 있습니다.

p${\displaystyle }$(${\displaystyle N,M}$ ;${\displaystyle n}$) -${\displaystyle p}$ (${\displaystyle N,M}$ -${\displaystyle 1}$ ;${\displaystyle n}$ )$${\$displaystyle$p ($N, M;n)$ - p ($N, M-1;n)}$가 n의 파티션을 최대 N개의 크기로 정확히 계산하고, 그러한 파티션의 각 부분에서 1을 빼면 n - M의 파티션이 최대 M개의 ^[15]파티션으로 계산됩니다.

가우스 이항 계수는 다음과 같이 정의됩니다.

가우스 이항 계수는 p(N, M;n)의 생성 함수와 등식에 의해 연관됩니다.

랭크와 더피 사각형

파티션의 순위는 최소 k개 이상의 크기의 부분을 포함하도록 가장 큰 k개입니다.예를 들어 파티션 4 + 3 + 3 + 2 + 1 + 1은 ≥ 3인 부분 3을 포함하지만 ≥ 4인 부분 4를 포함하지 않기 때문에 순위 3을 갖습니다.순위 r의 분할의 페러 다이어그램 또는 영 다이어그램에서 왼쪽 위에 있는 항목의 r × r 제곱을 더피 제곱이라고 합니다.

Durfee 사각형은 ^[16]다양한 파티션 ID의 증명에 조합론 내에서 응용 프로그램이 있습니다.그것은 또한 h-index의 형태로 실용적인 의미가 있습니다.

다른 통계량은 파티션(또는 다이슨 랭크)의 순위, 즉 k 부분이 ${\displaystyle {가장}_{}}$ 큰 k 부분의 파티션 λ k ${\displaystyle \lambda$ _${k$k$}$의 차이 λ k${\displaystyle {}_{}}$- ${\displaystyle k}${\$displaystyle \lambda$ _{k$}-k}$라고도 합니다.이 통계치(위에서 설명한 통계치와 무관함)는 라마누잔 합동 연구에서 나타납니다.

영의 격자

Young diagram을 포함하여 주어진 파티션에 대한 자연스러운 부분 순서가 있습니다.이 부분 순서 집합은 영의 격자로 알려져 있습니다.격자는 원래 표현 이론의 맥락에서 정의되었으며, 특성 0에서 모든 n에 대한 대칭 그룹_n S의 축소할 수 없는 표현을 설명하는 데 사용됩니다.또한 순수하게 조합적인 특성으로 상당한 연구를 받았습니다. 특히 미분 포셋의 동기를 부여하는 예입니다.

참고 항목

메모들

참고문헌

• Abramowitz, Milton; Stegun, Irene (1964). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. United States Department of Commerce, National Bureau of Standards. ISBN 0-486-61272-4.
• Andrews, George E. (1976). The Theory of Partitions. Cambridge University Press. ISBN 0-521-63766-X.
• Andrews, George E.; Eriksson, Kimmo (2004). Integer Partitions. Cambridge University Press. ISBN 0-521-60090-1.
• Apostol, Tom M. (1990) [1976]. Modular functions and Dirichlet series in number theory. Graduate Texts in Mathematics. Vol. 41 (2nd ed.). New York etc.: Springer-Verlag. ISBN 0-387-97127-0. Zbl 0697.10023. (라데마허의 공식에 대한 현대 교육학 개론은 5장 참조).
• Bóna, Miklós (2002). A Walk Through Combinatorics: An Introduction to Enumeration and Graph Theory. World Scientific Publishing. ISBN 981-02-4900-4. (Ferrers graph에 대한 토론을 포함하여 정수 파티션에 대한 주제에 대한 기본적인 소개)
• Hardy, G. H.; Wright, E. M. (2008) [1938]. An Introduction to the Theory of Numbers. Revised by D. R. Heath-Brown and J. H. Silverman. Foreword by Andrew Wiles. (6th ed.). Oxford: Oxford University Press. ISBN 978-0-19-921986-5. MR 2445243. Zbl 1159.11001.
• Lehmer, D. H. (1939). "On the remainder and convergence of the series for the partition function". Trans. Amer. Math. Soc. 46: 362–373. doi:10.1090/S0002-9947-1939-0000410-9. MR 0000410. Zbl 0022.20401. A(n)에 대한_k 주식(도함수 없음), 나머지 및 구식을 제공합니다.)
• Gupta, Hansraj; Gwyther, C.E.; Miller, J.C.P. (1962). Royal Society of Math. Tables. Vol. 4, Tables of partitions. (문자가 있고, 거의 완전한 서지를 가지고 있지만, 그들(그리고 아브라모위츠)은 화이트맨에 있는 A(n)의_k 셀버그 공식을 놓쳤습니다.)
• Macdonald, Ian G. (1979). Symmetric functions and Hall polynomials. Oxford Mathematical Monographs. Oxford University Press. ISBN 0-19-853530-9. Zbl 0487.20007. (섹션 I.1 참조)
• Nathanson, M.B. (2000). Elementary Methods in Number Theory. Graduate Texts in Mathematics. Vol. 195. Springer-Verlag. ISBN 0-387-98912-9. Zbl 0953.11002.
• Rademacher, Hans (1974). Collected Papers of Hans Rademacher. Vol. v II. MIT Press. pp. 100–07, 108–22, 460–75.
• Sautoy, Marcus Du. (2003). The Music of the Primes. New York: Perennial-HarperCollins. ISBN 9780066210704.
• Stanley, Richard P. (1999). Enumerative Combinatorics. Vol. 1 and 2. Cambridge University Press. ISBN 0-521-56069-1.
• Whiteman, A. L. (1956). "A sum connected with the series for the partition function". Pacific Journal of Mathematics. 6 (1): 159–176. doi:10.2140/pjm.1956.6.159. Zbl 0071.04004. (Selberg 공식을 제공합니다.더 오래된 형태는 셀버그의 유한 푸리에 확장입니다.)

외부 링크

• "Partition", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• 구획구성계산기
• Weisstein, Eric W. "Partition". MathWorld.
• 윌프, 허버트 S.
• 정수 시퀀스의 On-Line Encyclopedia에 대한 참조 테이블이 있는 파티션으로 계산
• FindStat 데이터베이스의 정수 파티션 항목
• 정수::CPAN의 Partition Perl 모듈
• 정수 파티션 생성을 위한 고속 알고리즘
• 모든 파티션 생성: 두 인코딩 비교
• Grime, James (April 28, 2016). "Partitions - Numberphile" (video). Brady Haran. Archived from the original on 2021-12-11. Retrieved 5 May 2016.