부정 굴절
Negative refraction이 글은 대부분의 독자들이 이해하기에는 너무 기술적인 것일 수도 있다. (2020년 7월)(이과 시기 |
부정 굴절은 더 흔히 관측되는 양의 굴절 특성과는 반대인 인터페이스에서 광선이 굴절되는 전자기 현상이다. 음의 굴절은 (전기) 허용도(ε) 및 (자기) 투과성(μ)에 대한 음의 값을 달성하도록 설계된 메타 물질을 사용하여 얻을 수 있다. 이 경우 물질은 음의 굴절 지수를 할당할 수 있다. 이런 물질을 '이중 음성' 물질이라고 부르기도 한다.[1]
음의 굴절은 일반적인 양의 위상 속도(즉, 양의 굴절률)를 가진 물질과 이국적인 음의 위상 속도(음의 굴절률)를 가진 물질 사이의 인터페이스에서 발생한다.
음상 속도
음상 속도(NPV)는 매질 내 광 전파의 속성이다. NPV의 정의는 서로 다르다. 가장 일반적인 것은 파동 벡터의 반대와 (아브라함) 포앵팅 벡터의 반대라는 빅토르 베셀라고의 원래 제안이다. 다른 정의에는 그룹 속도에 대한 파동 벡터 및 속도에 대한 에너지의 반대가 포함된다.[2] "위상 속도"는 위상 속도가 파형 벡터와 동일한 기호를 가지기 때문에 관습적으로 사용된다.
Veselago의 NPV를 결정하는 데 사용되는 일반적인 기준은 Poynting 벡터 및 파형 벡터의 도트 곱이 음(즉, P → k→< \script 이지만 이 정의는 공변량적이지 않다. 이러한 제약이 실질적으로 유의미한 것은 아니지만, 그 기준은 공변량 형태로 일반화되었다.[3] 베셀라고 NPV 매체는 오른손 법칙 대신 왼손 법칙을 따르는 평면파(전기장, 자기장, 파장 벡터)의 성분이 통과하기 때문에 왼손(메타) 재료라고도 불린다. '왼손잡이'와 '오른손잡이'라는 용어는 일반적으로 치랄매체를 지칭하는 용어로도 쓰이기 때문에 피하는 것이 일반적이다.
부 굴절률
전파 광장의 포아닌팅 벡터와 파동 벡터를 직접 고려하지 않고, 그 대신 물질의 반응을 직접 고려할 수 있다. 물질이 아치랄이라고 가정할 때 어떤 허용도( ()와 투과도(µ) 값이 음상 속도(NPV)를 초래하는지 고려할 수 있다. µ와 µ 모두 일반적으로 복잡하기 때문에, µ의 상상 부분은 수동(즉, 손실) 소재가 음수 굴절을 나타내려면 음수일 필요가 없다. 이러한 물질에서 음상 속도의 기준은 데핀과 라흐타키아가 도출해낸 것이다.
여기서 , 는 각각 µ와 µ의 실제 가치 부품이다. 활성물질의 경우 기준이 다르다.[4][5]
NPV 발생이 반드시 음의 굴절(음의 굴절 지수)을 의미하는 것은 아니다.[6][7] 일반적으로 굴절률 은(는) 다음을 사용하여 결정된다.
- = ± n
여기서 관례에 의해 에 대해 양의 제곱근을 선택하지만 NPV 재료에서는 음의 제곱근을 선택하여 파동 벡터와 위상 속도도 역전된다는 사실을 모방한다. 굴절률이란 파형 벡터가 빛의 광 주파수 및 전파 방향과 어떻게 관련이 있는지를 설명하는 파생량으로서, 물리적 상황과 하도록 n 의 기호를 선택해야 한다.
치랄 소재에
굴절률 은(는) 또한 처럴리티 {{\}에 따라 달라지며 그에 따라 다음과 같이 지정되는 좌우 원형 편극 파형에 대해 구별되는 값이 발생한다.
- = ± ± μ r r {\
{\ > r sqrton sqrton 이 경우 r {\ _{ 및/또는 r \mu \mu \ \mu \mu \ 치례로 인한 음의 굴절률은 펜드리 및 트레야코프 외 연구진이 예측했으며,[8][9] 2009년 플럼 외 연구진과 장 외 연구진이 동시에 독립적으로 처음 관측했다.[10][11]
굴절
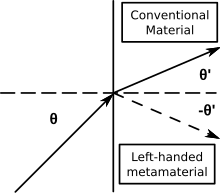
부정 굴절의 결과는 도표에 나타난 바와 같이 재료에 들어갈 때 광선이 정상의 같은 면과 스넬의 일반적인 법칙에 의해 굴절된다는 것이다.
참고 항목
- 음향 메타물질
- 메타물질
- 음지수 메타물질
- 메타물질 안테나
- 다자유분산 이론
- N-슬릿 간섭 방정식
- 퍼펙트 렌즈
- 광자성 메타물질
- 포토닉 크리스털
- 지진 메타물질
- 스플릿링 공진기
- 튜닝성 메타물질
전자기 상호작용
참조
- ^ Slyusar, Vadym I. (2009-10-10). "Metamaterials on antenna solutions" (PDF). Proceedings of International Conference on Antenna Theory and Techniques: 19–24. doi:10.1109/ICATT.2009.4435103 (inactive 31 October 2021).
{{cite journal}}: CS1 maint : 2021년 10월 현재 DOI 비활성화(링크) - ^ Veselago, Viktor G (1968-04-30). "THE ELECTRODYNAMICS OF SUBSTANCES WITH SIMULTANEOUSLY NEGATIVE VALUES OF ε AND μ". Soviet Physics Uspekhi. 10 (4): 509–514. Bibcode:1968SvPhU..10..509V. doi:10.1070/pu1968v010n04abeh003699. ISSN 0038-5670.
- ^ M. W. McCall (2008). "A Covariant Theory of Negative Phase Velocity Propagation". Metamaterials. 2 (2–3): 92. Bibcode:2008MetaM...2...92M. doi:10.1016/j.metmat.2008.05.001.
- ^ R. A. Depine and A. Lakhtakia (2004). "A new condition to identify isotropic dielectric-magnetic materials displaying negative phase velocity". Microwave and Optical Technology Letters. 41 (4): 315–316. arXiv:physics/0311029. doi:10.1002/mop.20127. S2CID 6072651.
- ^ P. Kinsler and M. W. McCall (2008). "Criteria for negative refraction in active and passive media". Microwave and Optical Technology Letters. 50 (7): 1804. arXiv:0806.1676. doi:10.1002/mop.23489.
- ^ Mackay, Tom G.; Lakhtakia, Akhlesh (2009-06-12). "Negative refraction, negative phase velocity, and counterposition in bianisotropic materials and metamaterials". Physical Review B. 79 (23): 235121. arXiv:0903.1530. Bibcode:2009PhRvB..79w5121M. doi:10.1103/PhysRevB.79.235121.
- ^ J. Skaar (2006). "On resolving the refractive index and the wave vector". Optics Letters. 31 (22): 3372–3374. arXiv:physics/0607104. Bibcode:2006OptL...31.3372S. CiteSeerX 10.1.1.261.8030. doi:10.1364/OL.31.003372. PMID 17072427. S2CID 606747.
- ^ Pendry, J. B. (2004). "A Chiral Route to Negative Refraction". Science. 306 (5700): 1353–5. Bibcode:2004Sci...306.1353P. doi:10.1126/science.1104467. PMID 15550665. S2CID 13485411.
- ^ Tretyakov, S.; Nefedov, I.; Shivola, A.; Maslovski, S.; Simovski, C. (2003). "Waves and Energy in Chiral Nihility". Journal of Electromagnetic Waves and Applications. 17 (5): 695. arXiv:cond-mat/0211012. doi:10.1163/156939303322226356. S2CID 119507930.
- ^ Plum, E.; Zhou, J.; Dong, J.; Fedotov, V. A.; Koschny, T.; Soukoulis, C. M.; Zheludev, N. I. (2009). "Metamaterial with negative index due to chirality" (PDF). Physical Review B. 79 (3): 035407. Bibcode:2009PhRvB..79c5407P. doi:10.1103/PhysRevB.79.035407.
- ^ Zhang, S.; Park, Y.-S.; Li, J.; Lu, X.; Zhang, W.; Zhang, X. (2009). "Negative Refractive Index in Chiral Metamaterials". Physical Review Letters. 102 (2): 023901. Bibcode:2009PhRvL.102b3901Z. doi:10.1103/PhysRevLett.102.023901. PMID 19257274.