베지어 곡선

베지어 곡선(/ ˈb ɛz.i.e ɪ/ BEH-zee-ay)은 컴퓨터 그래픽스 및 관련 분야에서 사용되는 매개 변수 곡선입니다. 이산 "관리점" 집합은 공식을 통해 매끄럽고 연속적인 곡선을 정의합니다. 일반적으로 곡선은 수학적 표현이 없거나 표현이 알려지지 않거나 너무 복잡한 실제 모양에 근접하도록 설계됩니다. 베지어 곡선은 1960년대에 르노 자동차의 차체를 위한 곡선을 디자인하기 위해 사용했던 프랑스 엔지니어 피에르 베지어(Pierre Bézier, 1910-1999)의 이름을 따서 명명되었습니다.^[3] 다른 용도로는 컴퓨터 글꼴 및 애니메이션 디자인이 있습니다.^[3] 베지어 곡선을 결합하여 베지어 스플라인을 형성하거나 더 높은 차원으로 일반화하여 베지어 표면을 형성할 수 있습니다.^[3] 베지어 삼각형은 후자의 특별한 경우입니다.

벡터 그래픽에서 베지어 곡선은 무한히 확장될 수 있는 매끄러운 곡선을 모델링하는 데 사용됩니다. "^{[note 1]}경로"는 이미지 조작 프로그램에서 일반적으로 언급되는 것처럼 연결된 베지어 곡선의 조합입니다. 경로는 래스터화된 이미지의 제한에 구속되지 않으며 수정하기에 직관적입니다.

베지어 곡선은 특히 애니메이션,^{[4][note 2]} 사용자 인터페이스 설계 및 눈 시선 제어 인터페이스의 평활 커서 궤적에서 시간 영역에서도 사용됩니다.^[5] 예를 들어, 베지어 곡선을 사용하여 단순히 단계당 고정된 픽셀 수로 이동하는 것이 아니라 A에서 B로 이동하는 아이콘과 같은 객체의 시간에 따른 속도를 지정할 수 있습니다. 애니메이터 또는 인터페이스 디자이너가 작업의 "물리적" 또는 "느낌"에 대해 이야기할 때, 그들은 문제의 이동 시간에 따른 속도를 제어하기 위해 사용되는 특정 베지어 곡선을 언급할 수 있습니다.

이는 예를 들어 용접 암의 움직임이 매끄러워야 불필요한 마모를 피할 수 있는 로봇공학에도 적용됩니다.

발명.

베지어 곡선의 수학적 기초인 번스타인 다항식은 1912년에 확립되었지만, 그 다항식은 50년 정도가 지난 1959년 수학자 폴 드 카스텔자우가 곡선을 평가하는 수치적으로 안정된 방법인 드 카스텔자우의 알고리즘을 개발할 때까지 그래픽에 적용되지 않았습니다. 프랑스 자동차 회사인 시트로 ë에서 처음으로 컴퓨터 지원 설계에 적용했습니다. De Casteljau의 방법은 프랑스에서 특허를 받았지만 1980년대까지^[7] 발표되지 않았고, 1960년대에 프랑스 엔지니어 Pierre Bézier에 의해 널리 발표되었습니다. Pierre Bézier는 그 다항식들을 독립적으로 발견하고 르노에서 자동차 차체를 디자인하는 데 사용했습니다.

구체적인 경우

베지어 곡선은 관리점 P에서 P까지의 집합으로 정의되며, 여기서 n은 곡선의 순서(선형의 경우 n = 1, 2차의 경우 2, 3 등)라고 합니다. 첫 번째 및 마지막 관리점은 항상 곡선의 끝점이지만 중간 관리점은 일반적으로 곡선 위에 놓이지 않습니다. 다음 절의 합계는 아핀 조합, 즉 계수의 합계가 1인 것으로 이해됩니다.

선형 베지어 곡선

서로 다른 점 P와₀ P가₁ 주어졌을 때, 선형 베지어 곡선은 이 두 점 사이의 선일 뿐입니다. 곡선은 다음과 같습니다.

${\displaystyle \mathbf {B} (t)=\mathbf {P} _{0}+t(\mathbf {P} _{1}-\mathbf {P} _{0})=(1-t)\mathbf {P} _{0}+t\mathbf {P} _{1},\ 0\leq t\leq 1}$

이것은 가장 단순하고 선형 보간에 해당합니다.^[8] 수량 $P{\displaystyle {\mathbf{}}_{}}$ ${\displaystyle {}_{}}$- P ${\displaystyle {\mathrm{}}_{}}$ ${\$} -$\mathbf {P} _{0}$은 시작점에서 종료점까지의 변위 벡터를 나타냅니다$$.

이차 베지어 곡선

2차 베지에 곡선은 주어진₀ 점 P₁, P₂, P에 의해 함수 B(t)에 의해 추적되는 경로입니다.

${\displaystyle \mathbf{B}}$(${\displaystyle \mathbf{}t}$) =${\displaystyle }$( 1${\displaystyle }$- $t$) [ ( $1$ - t ) P 0 + t P 1 ] + t [ ( 1 - t ) P 1 + t P 2 ], 0 ≤ t ≤ 1 {\displaystyle \mathbf {B} ${\displaystyle \mathbf{(}}$ t) = (1-t) [ (1-t)\mathbf {P} _{0} + t\mathbf {P} _{1} + t [ (1-t)\mathbf {P} _{1} + t\mathbf {P} _{2}, 0\leq t\leq 1}

이는 각각 P에서₀ P까지의₁ 선형 베지어₁ 곡선과₂ P에서 P까지의 선형 곡선에서 대응하는 점들의 선형 보간으로 해석될 수 있습니다. 앞의 방정식을 재배열하면 다음과 같은 결과가 나옵니다.

${\displaystyle \mathbf {B} (t)=(1-t)^{2}\mathbf {P} _{0}+2(1-t)t\mathbf {P} _{1}+t^{2}\mathbf {P} _{2},\ 0\leq t\leq 1.}$

이는 P에₁ 대한 대칭성을 강조하는 방식으로 작성할 수 있습니다.

${\displaystyle \mathbf {B} (t)=\mathbf {P} _{1}+(1-t)^{2}(\mathbf {P} _{0}-\mathbf {P} _{1})+t^{2}(\mathbf {P} _{2}-\mathbf {P} _{1}),\ 0\leq t\leq 1.}$

이는 t에 대한 베지어 곡선의 도함수를 즉시 제공합니다.

${\displaystyle \mathbf {B} '(t)=2(1-t)(\mathbf {P} _{1} -\mathbf {P} _{0})+2t(\mathbf {P} _{2} -\mathbf {P} _{1}),}$

이로부터 P와₀ P에서₂ 곡선에 대한 접선은 P에서₁ 교차한다고 결론지을 수 있습니다. t가 0에서 1로 증가함에 따라 곡선은 P에서₀ P₁ 방향으로 출발한 다음 휘어져서₁ P 방향에서 P에₂ 도달합니다.

t에 대한 베지어 곡선의 두 번째 도함수는

${\displaystyle \mathbf {B} ''(t)=2(\mathbf {P} _{2}-2\mathbf {P} _{1}+\mathbf {P} _{0}).$

큐빅 베지어 곡선

평면 또는 고차원 공간에 있는 네 개의₀ 점₁ P, P, P₂, P는₃ 입방 베지어 곡선을 정의합니다. 곡선은 P를₁ 향해 가는 P에서₀ 시작하여 P의₂ 방향에서 P에₃ 도달합니다. 일반적으로 P₁ 또는 P를₂ 통과하지 않으며, 이 점들은 방향 정보를 제공하기 위한 것일 뿐입니다. P와₁ P₂ 사이의 거리는 곡선이 P₂ 방향으로 향하기 전에₁ P 방향으로 이동하는 "거리"와 "속도"를 결정합니다.

점 P_i, P_j, P로_k 정의되는 이차 베지어 곡선에 대해 B_Pi,Pj,Pk(t)를 쓰면, 이차 베지어 곡선은 두 이차 베지어 곡선의 아핀 조합으로 정의할 수 있습니다.

${\displaystyle \mathbf {B} (t)=(1-t)\mathbf {B} _{\mathbf {P} _{0},\mathbf {P} _{1},\mathbf {P} _{2}}(t)+t\mathbf {B} _{\mathbf {P} _{1},\mathbf {P} _{2},\mathbf {P} _{3}}(t),\ 0\leq t\leq 1.}$

곡선의 명시적인 형태는 다음과 같습니다.

${\displaystyle \mathbf {B} (t)=(1-t)^{3}\mathbf {P} _{0}+3(1-t)^{2}t\mathbf {P} _{1}+3(1-t)t^{2}\mathbf {P} _{2}+t^{3}\mathbf {P} _{3},\ 0\leq t\leq 1.}$

일부₁ P와₂ P 선택의 경우 곡선이 교차하거나 첨자를 포함할 수 있습니다.

4개의 구별되는 점들로 이루어진 어떤 급수도 4개의 점들을 모두 순서대로 통과하는 3차 베지에 곡선으로 변환될 수 있습니다. 어떤 입방체 베지어 곡선의 시작점과 끝점, 그리고 곡선을 따라 t = 1/3, t = 2/3에 해당하는 점들이 주어지면, 원래 베지어 곡선에 대한 통제점들을 복구할 수 있습니다.

t에 대한 입방체 베지어 곡선의 도함수는

${\displaystyle \mathbf {B} '(t)=3(1-t)^{2}(\mathbf {P} _{1}-\mathbf {P} _{0})+6(1-t)t(\mathbf {P} _{2}-\mathbf {P} _{1})+3t^{2}(\mathbf {P} _{3}-\mathbf {P} _{2})\,.}$

t에 대한 베지어 곡선의 두 번째 도함수는

${\displaystyle \mathbf {B} ''(t)=6(1-t)(\mathbf {P} _{2}-2\mathbf {P} _{1}+\mathbf {P} _{0})+6t(\mathbf {P} _{3}-2\mathbf {P} _{2}+\mathbf {P} _{1})\,.}$

일반적 정의

베지어 곡선은 어떤 차수 n에 대해서도 정의될 수 있습니다.

재귀적 정의

n도의 베지어 곡선에 대한 재귀적 정의는 n도 - 1도의 두 베지어 곡선에서 대응하는 한 쌍의 점 대 점 선형 조합(선형 보간)으로 표현합니다.

$B{\displaystyle {\mathbf{}}_{}}$ ${\displaystyle {{\mathbf{}}_{}}_{}}$ 0 ${\displaystyle {{}_{}{\mathbf{}}_{}}_{}}$ ${\displaystyle {{}_{}}_{}}$… ${\displaystyle {{}_{}}_{}}$ ${\$ ${\mathbf${$P$}$_{\mathbf {P} _{1}\ldots \mathbf {P} _{k}}$는 임의의₀ 점 P₁, P, ..., P에_k 의해 결정되는 베지어 곡선을 나타냅니다$$. 그런 다음 시작하려면,

${\displaystyle \mathbf {B}_{\mathbf {P}_{0}}(t)=\mathbf {P}_{\text{ 및}}$

${\displaystyle \mathbf {B} (t)=\mathbf {B} _{\mathbf {P} _{0}\mathbf {P} _{1}\ldots \mathbf {P} _{n} _{n}} = (1-t)\mathbf {B} _{\mathbf {P} _{1}\ldots \mathbf {P} _{n-1} _(t)+t\mathbf {B} _{\mathbf {P} _{1}\mathbf {P} _{2}\ldots \mathbf {P} _{n} (t)}$

이 재귀는 아래 애니메이션에 설명되어 있습니다.

명시적 정의

공식은 다음과 같이 명시적으로 표현할 수 있습니다(여기서 t와⁰ (1-t)⁰는 [0,1] 전체에 걸쳐 연속적으로 1이 되도록 확장됩니다).

${\displaystyle {\begin{aligned}\mathbf {B} (t)&=\sum _{i=0}^{n}{n \choose i}(1-t)^{n-i}t^{i}\mathbf {P} _{i}\\&=(1-t)^{n}\mathbf {P} _{0}+{n \choose 1}(1-t)^{n-1}t\mathbf {P} _{1}+\cdots +{n \choose n-1}(1-t)t^{n-1}\mathbf {P} _{n-1}+t^{n}\mathbf {P} _{n},&&0\leqslant t\leqslant 1\end{aligned}}}$

여기서${\displaystyle }$(${\displaystyle n\genfrac{}{}{0ex}{}{}{}}$ ${\displaystyle \genfrac{}{}{0ex}{}{i}{})}$ ${\$ i$}}$는 이항 계수입니다.

예를 들어, n = 5일 때:

${\displaystyle {\begin{aligned}\mathbf {B} (t)&=(1-t)^{5}\mathbf {P} _{0}+5t(1-t)^{4}\mathbf {P} _{1}+10t^{2}(1-t)^{3}\mathbf {P} _{2}+10t^{3}(1-t)^{2}\mathbf {P} _{3}+5t^{4}(1-t)\mathbf {P} _{4}+t^{5}\mathbf {P} _{5},&&0\leqslant t\leqslant 1.\end{align}}}$

용어.

일부 용어는 이러한 모수 곡선과 관련이 있습니다. 우리는 가지고 있다.

${\displaystyle \mathbf {B} (t)=\sum _{i=0}^{n}b_{i,n}(t)\mathbf {P} _{i},\ \ \ 0\leq t\leq 1}$

여기서 다항식들은

${\displaystyle b_{i,n}(t)={n \choose i}t^{i}(1-t)^{n-i},\ \ \ i=0,\ldots ,n}$

n차의 번스타인 기저 다항식으로 알려져 있습니다.

t = 1, (1 - $t$) = 1 이항 계수인 (n i) {\displaystyle \scriptstyle {n \choose i}}는 다음과 같습니다.

${\displaystyle {n \choose i}={\frac {n!}{i!(n-i)!}}.}$

점 P는_i 베지어 곡선의 관리점이라고 합니다. 베지어 점을 선으로₀ 연결하여 P로 시작하여 P로_n 끝나는 다각형을 베지어 다각형(또는 제어 다각형)이라고 합니다. 베지어 다각형의 볼록한 선체는 베지어 곡선을 포함합니다.

다항식

베지어 곡선을 덜 단순한 번스타인 다항식의 합 대신 다항식으로 표현하는 것이 바람직하기도 합니다. 곡선의 정의에 이항 정리를 적용한 후 약간의 재배열을 수행하면 다음과 같은 결과를 얻을 수 있습니다.

${\displaystyle \mathbf {B} (t)=\sum _{j=0}^{n}{t^{j}\mathbf {C}_{j}}$

어디에

${\displaystyle \mathbf {C}_{j}={\frac {n!}{(n-j)!}}\sum _{i=0}^{j}{\frac {(-1)^{i+j}\mathbf {P} _{i}}{i!(j-i)!}}=\prod _{m=0}^{j-1}(n-m)\sum _{i=0}^{j}{\frac {(-1)^{i+j}\mathbf {P} _{i}}{i!(j-i)!}}.}$

${\displaystyle {}_{}}$ ${\$를 $B{\displaystyle \mathbf{}}$(${\displaystyle t)}$ ${\displaystyle \mathbf {B}(t)}$의 많은 평가 전에 계산할 수$$ 있다면 이는 실용적일 수 있습니다$.$ 그러나 고차 곡선에는 숫자 안정성이 부족할 수 있으므로 주의해야 합니다(이 경우 de Casteljau의 알고리즘을 사용해야 함). 빈 제품은 1입니다.

특성.

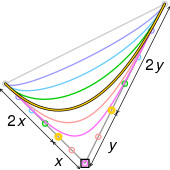
• 곡선은 $P{\displaystyle {\mathbf{}}_{}}$ ${\displaystyle {\mathrm{}}_{}}$ ${\$ _${0}$에서 시작하여$$ $P{\displaystyle {\mathbf{}}_{}}$ ${\displaystyle {}_{}}$ ${\$에서 끝납니다$.$ 이는 소위 끝점 보간 속성입니다.
• 모든 관리점이 공선인 경우에만 곡선이 선이 됩니다.
• 곡선의 시작과 끝은 각각 베지어 다각형의 첫 번째와 마지막 부분에 접합니다.
• 곡선은 임의의 점에서 두 개의 하위 곡선으로 분할되거나 임의의 많은 하위 곡선으로 분할될 수 있으며, 각 곡선은 베지어 곡선이기도 합니다.
• 원과 같이 단순해 보이는 곡선들은 베지어 곡선이나 조각 형태의 베지어 곡선으로 정확하게 설명할 수 없지만, 4입방체 베지어 곡선은 최대 반경 오차가 1,000분의 1 미만인 원과 근사할 수 있습니다. 각 내부 제어 지점(또는 오프라인 지점)이 단위 원의 외부 제어 지점에서 가로 또는 세로로 $4{\displaystyle \frac{(2}{}}$- ${\displaystyle \frac{1)}{}}$ 3 ${\displaystyle \textstyle {\frac {4\left$({\$sqrt {$2}-1$\right$)}{3}}입니다. 보다 일반적으로, 각 내부 제어점이 단위 원의 외부 제어점으로부터 $43$ ${\displaystyle tan}$⁡${\displaystyle (}$t $/$ 4) ${\displaystyle {\frac {4}{3}}\$tan(t/4)}인 경우, $n-피스$ 큐빅 베지어 곡선은 원과 근사할 수 있습니다. 여기서 t = 2$$π$$/ n {\$textstyle t$ = 2\pi / n}(즉, ). ${\displaystyle t}$ $=$ ${\displaystyle 3}$$60$ ∘ / n {\displaystyl${\displaystyle e}$ t = 360^{\circ}/n}), n > 2 {\displaystyle n> 2}.
• 모든 2차 베지에 곡선은 또한 3차 베지에 곡선이며, 더 일반적으로 모든 n차 베지에 곡선은 임의의 m > n에 대한 m차 곡선이기도 합니다. 구체적으로, 기준점 ${\displaystyle {\mathrm{}}_{}}$ 0${\displaystyle {}_{}\dots ,}$ ${\displaystyle {}_{}}$ ${\$ _${0},\,\dots,\,\mathbf {P}$ _${n}}$는 기준점 ${\displaystyle {\mathrm{}}_{}^{}}$ $0{\displaystyle {\mathbf{}}_{}^{}\text{'},}$ …, ${\displaystyle P{\mathbf{}}_{}^{}{\mathrm{n}}_{}^{}}$ +${\displaystyle {}_{}^{}}$1${\displaystyle {}_{}^{}}$ ${\$ where ${\displaystyle \mathbf {P} '_{k}={\tfrac {k}{n+1}}\mathbf {P} _{k-1}+\left(1-{\tfrac {k}{n+1}}\right)\mathbf {P} _{k}}$, ${\displaystyle \forall k=0,\,1,\,\dots ,\,n,\,$$n+$${\displaystyle 1_{}}$$}$을 정의하고 ${\displaystyle {}_{}}$ n${\displaystyle {}_{}}$+ 1 : $=$ ${\displaystyle {}_{}}$ ${\displaystyle$$\mathbf {P}$ _${n$+1}:$=$\mathbf {P} _{0}, P - 1 : $=$ P {\displaystyle \mathbf {P} _{-1}: $=$\mathbf {P} _{n}을 정의합니다.
• 베지어 곡선은 변동 감소 특성을 가지고 있습니다. 이것이 직관적인 용어로 의미하는 것은 베지어 곡선이 관리점의 다각형보다 더 "환산"하지 않고 실제로는 그보다 더 적게 "환산"할 수 있다는 것입니다.^[10]
• 차수 n Bézier 곡선에는 로컬 제어가 없습니다. 즉, 관리점에 대한 변경은 재계산을 필요로 하므로 전체 곡선의 측면에 영향을 미칩니다. "변경된 관리점에서 멀어질수록 곡선의 변경이 작습니다."^[11]
• 2보다 높은 차수의 베지어 곡선은 교차하거나 관리점의 특정 선택에 대한 첨자를 가질 수 있습니다.

2차 곡선은 포물선 세그먼트입니다.

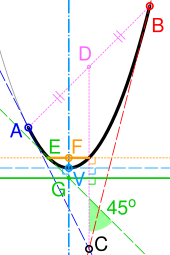
이차 베지어 곡선은 포물선의 한 부분이기도 합니다. 포물선은 원뿔 단면이므로, 일부 자료에서는 이차 베지에를 "원뿔 호"라고 부릅니다.^[12] 오른쪽 그림을 참조하여 포물선의 중요한 특징을 다음과 같이 도출할 수 있습니다.^[13]

1. 곡선의 끝점(A 및 B)에서 포물선에 대한 접선은 관리점(C)에서 교차합니다.
2. D가 AB의 중간점이면 CD(대시선)에 수직인 곡선의 접선은 정점(V)을 정의합니다. 대칭축(대시점 시안)은 V를 통과하며 접선에 수직입니다.
3. E는 CD에 대해 45° 접선을 갖는 곡선의 한 점입니다(초록색). G가 이 접선과 축의 교점이라면, G를 지나 CD에 수직인 선은 직선(녹색 실선)입니다.
4. 초점(F)은 축과 선이 E를 통과하고 CD(점이 있는 노란색)에 수직인 교차점에 있습니다. 라투스 직장은 곡선 내 선분(단색 노란색)입니다.

도함수

차수 n의 곡선에 대한 도함수는

${\displaystyle \mathbf {B} '(t)=n\sum _{i=0}^{n-1}b_{i,n-1}(t)(\mathbf {P} _{i+1}-\mathbf {P} _{i}).}$

Bézier 곡선 구성

선형곡선

점 B(t)가 P에서₀ P로의₁ 이동을 따라 진행한 진행률(0 ~ 1)을 나타내자. 예를 들어, t=0.25일 때, B(t)는 점 P에서 P까지의 거리의 1/4입니다. t가 0에서 1까지 변하므로 B(t)는₀ P에서₁ P로 선을 그립니다.

선형 베지어 곡선의 애니메이션, [0,1]의 t

이차곡선

2차 베지에 곡선의 경우 t가 0에서 1까지 변하는 중간점₀ Q와₁ Q를 만들 수 있습니다.

• 점 Q₀(t)는 P부터₀ P까지₁ 다양하며 선형 베지어 곡선을 설명합니다.
• 점 Q₁(t)는 P부터₁ P까지₂ 다양하며 선형 베지어 곡선을 설명합니다.
• 점₀ B(t)는 Q(t)에서 Q₁(t) 사이에 선형으로 보간되며 2차 베지어 곡선을 설명합니다.

이차 베지어 곡선의 구축		[0,1]에서 t인 2차 베지어 곡선의 애니메이션

고차곡선

고차 곡선의 경우 그에 상응하는 더 많은 중간 점이 필요합니다. 3차 곡선의 경우 선형 베지어 곡선을 설명하는 중간점₀ Q, Q₁, Q를₂ 그리고 이차 베지어 곡선을 설명하는 점 R과₀ R을 구성할₁ 수 있습니다.

입방체 베지어 곡선의 구축		입방체 베지어 곡선의 애니메이션, t(0,1)

4차 곡선의 경우 선형 베지에 곡선을 설명하는 중간점₀ Q, Q, Q₁₂, Q₃, 2차 베지에 곡선을 설명하는 점 R₀, R₁ 및 R₂, 입방형 베지에 곡선을 설명하는 점 S₀ 및 S를₁ 구성할 수 있습니다.

사분위수 베지에 곡선의 구축		[0,1]에서 t 사분위수 베지어 곡선의 애니메이션

5차 곡선의 경우 유사한 중간 점을 구성할 수 있습니다.

5차 베지어 곡선의 애니메이션, 빨간색으로 [0,1] t. 각 하위 차수에 대한 베지어 곡선도 표시됩니다.

이러한 표현은 데 카스텔자우의 알고리즘에서 베지어 곡선을 계산하는 데 사용된 프로세스에 의존합니다.^[14]

베지어 곡선의 간격띄우기(또는 쓰다듬기)

수학에서 오프셋 또는 평행 곡선(철도 선로의 레일 사이의 오프셋과 같이 원래 곡선과 "평행"하는 것)이라고 불리는 주어진 베지어 곡선에서 고정된 오프셋에 있는 곡선은 베지어 곡선으로 정확히 형성될 수 없습니다(일부 사소한 경우를 제외하고). 일반적으로, 입방체 베지어의 양면 오프셋 곡선은 10차 대수^[15] 곡선이고, 더 일반적으로 n차의 베지어에 대해 양면 오프셋 곡선은 4n - 2차 대수 곡선입니다.^[16] 그러나 일반적으로 실용적인 목적을 위해 적절한 근사치를 제공하는 휴리스틱 방법이 있습니다.^[17]

벡터 그래픽스 분야에서 대칭적으로 거리가 있는 두 개의 오프셋 곡선을 그리는 것을 스트로킹(Bézier 곡선 또는 일반적으로 여러 개의 Bézier 세그먼트의 경로)이라고 합니다.^[15] 오프셋 곡선에서 채워진 베지어 윤곽으로의 변환은 베지어 곡선을 쓰다듬어야 하는 메타폰트에 정의된 글꼴을 더 널리 사용되는 포스트스크립트 유형 1 글꼴로 변환하는 데 실질적으로 중요하며, (효율적인 목적을 위해) 수학적으로 더 간단한 (자기 교집합이 아닌) 베지어 곡선으로 정의된 윤곽을 채우는 작업만 필요합니다.^[18]

고도

n도의 베지어 곡선은 같은 모양의 n도+1도의 베지어 곡선으로 변환될 수 있습니다. 소프트웨어가 특정 정도의 베지어 곡선만 지원하는 경우 유용합니다. 예를 들어, 입방 베지어 곡선에서만 작동할 수 있는 시스템은 동등한 입방 표현을 사용하여 2차 곡선에서 암묵적으로 작동할 수 있습니다.

차수 상승을 수행하려면 등식 $B$ (${\displaystyle }$t${\displaystyle }$) =${\displaystyle }$( ${\displaystyle 1}$-$$t ) B ( $t$) + t B ( t )를 사용합니다$.$ {\displaystyle \mathbf {B} ( t) = (1-t)\mathbf {B} ( t) + t\mathbf {B} ( t).$}$각$$ 성분 ${\displaystyle {,}_{}}$ ${\displaystyle n_{}t)}$ ${\displaystyle {}_{}}$ ${\$ _${i,n}(t)\mathbf {P}$ _${i}$는 (1 - t)와 t를 곱한 값이므로 값을 변경하지 않고 차수를 1씩 증가시킵니다. 2에서 3으로 도수가 증가하는 예는 다음과 같습니다.

${\displaystyle {\begin{aligned}(1-t)^{2}\mathbf {P} _{0}+2(1-t)t\mathbf {P} _{1}+t^{2}\mathbf {P} _{2}&=(1-t)^{3}\mathbf {P} _{0}+2(1-t)^{2}t\mathbf {P} _{1}+(1-t)t^{2}\mathbf {P} _{2}+(1-t)^{2}t\mathbf {P} _{0}+2(1-t)t^{2}\mathbf {P} _{1}+t^{3}\mathbf {P} _{2}\\&=(1-t)^{3}\mathbf {P} _{0}+(1-t)^{2}t\left(\mathbf {P} _{0}+2\mathbf {P} _{1}\right)+(1-t)t^{2}\left(2\mathbf {P} _{1}+\mathbf {P} _{2}\right)+t^{3}\mathbf {P} _{2}\\&=(1-t)^{3}\mathbf {P} _{0}+3(1-t)^{2}t{\tfrac {1}{3}}\left(\mathbf {P} _{0}+2\mathbf {P} _{1}\right)+3(1-t)t^{2}{\tfrac {1}{3}}\left(2\mathbf {P} _{1}+\mathbf {P} _{2}\right)+t^{3}\mathbf {P} _{2}\end{aligned}}$

임의의 n에 대하여 우리는 동등성을 사용합니다.

${\displaystyle {\begin{cases}{n+1 \choose i}(1-t)\mathbf {b} _{i,n}={n \choose i}\mathbf {b} _{i,n+1}\\{n+1 \choose i+1}t\mathbf {b} _{i,n}={n \choose i}\mathbf {b} _{i+1,n+1}\end{cases}}\quad \implies \quad {\begin{cases}(1-t)\mathbf {b} _{i,n}={\frac {n+1-i}{n+1}}\mathbf {b} _{i,n+1}\\t\mathbf {b} _{i,n}={\frac {i+1}{n+1}}\mathbf {b} _{i+1,n+1}\end{case}}$

따라서:

${\displaystyle {\begin{aligned}\mathbf {B} (t)&=(1-t)\sum _{i=0}^{n}\mathbf {b} _{i,n}(t)\mathbf {P} _{i}+t\sum _{i=0}^{n}\mathbf {b} _{i,n}(t)\mathbf {P} _{i}\\&=\sum _{i=0}^{n}{\frac {n+1-i}{n+1}}\mathbf {b} _{i,n+1}(t)\mathbf {P} _{i}+\sum _{i=0}^{n}{\frac {i+1}{n+1}}\mathbf {b} _{i+1,n+1}(t)\mathbf {P} _{i}\\&=\sum _{i=0}^{n+1}\left({\frac {i}{n+1}}\mathbf {P} _{i-1}+{\frac {n+1-i}{n+1}}\mathbf {P} _{i}\right)\mathbf {b} _{i,n+1}(t)\\&=\sum _{i=0}^{n+1}\mathbf {b} _{i,n+1}(t)\mathbf {P'} _{i}\end{aligned}}}$

${\displaystyle {\mathrm{임의}}_{}}$의 $P{\displaystyle {\mathbf{}}_{}}$- 1 ${\$ _${-1}}$ $및$ ${\displaystyle {}_{}}$+ ${\displaystyle 1_{}}$ ${\$ _${n+1}$을 소개합니다$.$

따라서 새로운 관리점은^[19]

${\displaystyle \mathbf {P'} _{i}={\frac {i}{n+1}}\mathbf {P} _{i-1}+{\frac {n+1-i}{n+1}}\mathbf {P} _{i},\quad i=0,\ldots ,n+1.}$

반복도 상승

정도 상승의 개념을 제어 다각형 R에서 반복하여 제어 다각형 R, R₁, R₂ 등의 시퀀스를 얻을 수 있습니다. r차 상승 후, 다각형 R은_r 다음과 같이 주어진 정점 P_0,r, P, P_1,r2,r, ..., P를_n+r,r 갖습니다.

${\displaystyle \mathbf {P} _{i,r}=\sum _{j=0}^{n}\mathbf {P} _{j}{\tbinom {n}{j}}{\frac {\tbinom {r}{i-j}}{\tbinom {n+r}{i}}}.}$

또한 기저 베지어 곡선 B에 대하여,

${\displaystyle \mathbf {\lim_{r\to \infty}R_{r}} =\mathbf {B}.}$

유리 베지어 곡선

합리적인 베지어 곡선은 임의의 모양에 더 가까운 근사치를 제공하기 위해 조정 가능한 가중치를 추가합니다. 분자는 가중 번스타인 형태의 베지어 곡선이고 분모는 번스타인 다항식의 가중합입니다. 유리 베지어 곡선은 다른 용도 중에서도 원뿔 곡선을 포함한 원뿔 단면의 세그먼트를 정확하게 표현하는 데 사용될 수 있습니다.^[20]

n + 1개의 관리점 P₀, ..., P가_n 주어지면 유리 베지어 곡선은 다음과 같이 나타낼 수 있습니다.

${\displaystyle \mathbf {B} (t)={\frac {\sum _{i=0}^{n}b_{i,n}(t)\mathbf {P} _{i}w_{i}}{\sum _{i=0}^{n}b_{i,n}(t)w_{i}}},}$

아니면 간단히

${\displaystyle \mathbf {B} (t)={\frac {\sum _{i=0}^{n}{n \choose i}t^{i}(1-t)^{n-i}\mathbf {P} _{i}w_{i}}{\sum _{i=0}^{n}{n \choose i}t^{i}(1-t)^{n-i}w_{i}}}.}$

무게에 대한 실수 외에 숫자 체계를 사용하여 표현을 확장할 수 있습니다. 복소 평면에서 가중치가 {${\displaystyle }$ ${\displaystyle i}},$ {1} 및 ${\displaystyle i}${\$displaystyle -i$인 점 {1}, {1}은 반지름이 1인 전체 원을 생성합니다. 원 위에 점과 무게가 있는 곡선의 경우 곡선 모양을 변경하지 않고 무게를 조정할 수 있습니다.^[21] 위 곡선의 중심 가중치를 1.35508만큼 스케일링하면 보다 균일한 파라미터를 얻을 수 있습니다.

적용들

컴퓨터 그래픽스

베지어 곡선은 컴퓨터 그래픽에서 부드러운 곡선을 모델링하는 데 널리 사용됩니다. 곡선이 제어점의 볼록한 선체에 완전히 포함되어 있으므로 점을 그래픽으로 표시하여 직관적으로 곡선을 조작하는 데 사용할 수 있습니다. 곡선의 제어점에 각각의 변환을 적용하여 변환 및 회전과 같은 아핀 변환을 곡선에 적용할 수 있습니다.

2차 및 3차 베지어 곡선이 가장 일반적입니다. 도수가 높은 곡선은 평가하기에 계산 비용이 더 많이 듭니다. 더 복잡한 모양이 필요할 때 낮은 차수의 베지어 곡선을 함께 패치하여 합성 베지어 곡선을 생성합니다. 벡터 그래픽스 언어(예: 포스트스크립트), 벡터 그래픽스 표준(예: SVG), 벡터 그래픽스 프로그램(예: 아트라인, 타임웍스 퍼블리셔, 어도비 일러스트레이터, 코렐드로, 잉크스케이프, 알레그로)에서 복합 베지어 곡선은 일반적으로 "경로"라고 합니다. 베지어 곡선을 꼬임이 없는 합성 베지어 곡선으로 결합하기 위해 G1 연속성이라는 특성은 두 구성 베지어 곡선이 만나는 기준점을 양쪽의 두 기준점에 의해 정의된 선 위에 놓도록 강요하기에 충분합니다.

베지어 곡선을 스캔 변환(래스터라이징)하는 가장 간단한 방법은 밀접하게 이격된 많은 지점에서 곡선을 평가하고 선분의 근사 시퀀스를 스캔 변환하는 것입니다. 그러나 점들이 너무 멀리 떨어져 있을 수 있기 때문에 래스터화된 출력이 충분히 매끄러워 보이는 것은 아닙니다. 반대로 곡선이 선형에 가까운 영역에서 너무 많은 점을 생성할 수 있습니다. 일반적인 적응 방법은 재귀적 세분화로, 곡선의 관리점을 검사하여 곡선이 작은 공차 내에 있는 선에 근접하는지 확인합니다. 그렇지 않은 경우 곡선을 매개변수적으로 0 ≤ t ≤ 0.5 및 0.5 ≤ t ≤ 1의 두 세그먼트로 세분화하고 각 절반에 대해 동일한 절차를 재귀적으로 적용합니다. 전방 차이 방법도 있지만 오류 전파를 분석하려면 매우 주의해야 합니다.^[23]

베지어가 각 스캔 라인과 교차하는 분석 방법은 (입방 베지어의 경우) 입방 다항식의 근을 찾는 것과 여러 근을 다루는 것을 포함하므로 실제로는 자주 사용되지 않습니다.^[23]

메타폰트에서 사용되는 래스터화 알고리즘은 곡선을 이산화하는 것을 기반으로 하므로 픽셀 경계를 따라 순수하게 수직 또는 순수하게 수평인 일련의 "루크 무브(roook moves)"로 근사화됩니다. 이를 위해 먼저 평면을 8개의 45° 섹터(좌표축과 두 개의 선 $y$ =${\displaystyle }$± ${\$displaystyle y =\pm x}에 의해)로 분할한 다음 곡선을 더 작은 세그먼트로 분해하여 곡선 세그먼트의 방향을 한 섹터 내에 유지합니다. 곡선 속도는 2차 다항식이므로, 이 선들 중 하나와 평행한 $t{\displaystyle }$ ${\displaystyle t}$ 값을$$ 찾는 것은 2차 방정식을 풀어서 할 수 있습니다. 각 세그먼트 내에서 수평 또는 수직 이동이 지배적이며, 끝점 좌표에서 한 방향의 총 계단 수를 읽을 수 있습니다. 예를 들어 오른쪽으로 0~45° 섹터 수평 이동이 지배적이므로 곡선이 오른쪽으로 한 계단 올라야 할 계단을 결정하기만 하면 됩니다.^[24]

이 래스터화를 수행하는 징글의 선묘 알고리즘은 곡선을 유리 조각으로 세분화하여 각 픽셀 위치의 오차를 계산하여 곡선을 반복하면서 합성 오차에 따라 45° 각도로 진행하거나 직선으로 진행하는 변형된 곡선 형태도 있습니다. 이렇게 하면 다음 단계 계산이 일련의 정수 덧셈과 뺄셈으로 줄어듭니다.^[25]

애니매이션

Adobe Flash 및 Synfig와 같은 애니메이션 애플리케이션에서 베지어 곡선은 움직임과 같은 윤곽을 그리기 위해 사용됩니다. 사용자는 베지어 곡선으로 원하는 경로의 윤곽을 표시하고, 응용 프로그램은 객체가 경로를 따라 이동하는 데 필요한 프레임을 만듭니다.^[26][27]

3D 애니메이션에서 베지어 곡선은 키프레임 보간을 위한 2D 곡선뿐만 아니라 3D 경로를 정의하는 데 종종 사용됩니다.^[28] 베지어 곡선은 현재 CSS, 자바스크립트, 자바Fx 및 플러터 SDK에서 애니메이션 완화를 제어하는 데 매우 자주 사용됩니다.^[4]

글꼴

TrueType 글꼴은 2차 Bézier 곡선으로 구성된 합성 Bézier 곡선을 사용합니다. 다른 언어 및 이미징 도구(예: PostScript, 점근선, 메타폰트, SVG)는 곡선 모양을 그리기 위해 입방체 베지어 곡선으로 구성된 합성 베지어를 사용합니다. OpenType 글꼴은 OpenType 래퍼의 기반이 되는 글꼴 기술에 따라 두 가지 종류의 곡선을 사용할 수 있습니다.^[29]

FreeType과 같은 글꼴 엔진은 글꼴 래스터화라고 하는 프로세스를 사용하여 픽셀화된 표면에 글꼴의 곡선(및 선)을 그립니다.^[12] 일반적으로 글꼴 엔진과 벡터 그래픽 엔진은 일련의 선형 또는 원형 세그먼트로 그릴 수 있을 정도로 곡선이 평평한 지점까지 재귀적으로 분할하여 베지어 곡선을 렌더링합니다. 정확한 분할 알고리즘은 구현에 따라 다르며, 필요한 정밀도에 도달하고 단일음이 아닌 국소적인 곡률 변화를 피하기 위해 평탄도 기준만 존중해야 합니다. 마이크로소프트 엑셀에 있는 차트의 "원활한 곡선" 기능도 이 알고리즘을 사용합니다.^[30]

원과 타원의 호는 베지어 곡선으로 정확히 표현될 수 없기 때문에, 그것들은 먼저 베지어 곡선으로 근사되고, 그것들은 차례로 원의 호로 근사됩니다. 임의의 정밀도로 점증적으로 렌더링할 수 있는 원 또는 타원의 호를 사용하여 모든 베지어 곡선의 근사치도 존재하므로 비효율적입니다. 기하학적 구조가 가속화된 최신 하드웨어 그래픽 어댑터에서 사용되는 또 다른 접근 방식은 모든 베지어 및 원뿔 곡선(또는 표면)을 정확히 NURBS로 변환할 수 있으며, 이는 필요한 평탄 조건에 도달하기 위해 먼저 곡선을 재귀적으로 분할하지 않고 점진적으로 렌더링할 수 있습니다. 이 접근법은 또한 모든 선형 또는 원근형 2D 및 3D 변환 및 투영에서 곡선 정의를 유지합니다.^{[citation needed]}

로봇공학

경로가 주변의 장애물이나 물체와 충돌하는지 여부를 명확하게 표시할 수 있는 제어 다각형의 능력 덕분에 베지어 곡선은 로봇 공학에서 엔드 이펙터의 궤적을 생성하는 데 사용될 수 있습니다.^[31] 또한 Bézier 곡선을 사용하여 관절 공간 궤적을 정확하게 구별할 수 있습니다. 결과적으로, 관절 공간 궤적의 도함수는 로봇 조작기의 역학 및 제어 노력(토크 프로파일)의 계산에 사용됩니다.^[31]

참고 항목

• 베지어 표면
• B스플라인
• GEM/4 및 GEM/5
• 에르미트 곡선
• NURBS
• 스트링 아트 – 베지어 곡선은 또한 많은 일반적인 형태의 스트링 아트에 의해 형성되며, 여기서 스트링은 못의 틀에 걸쳐 루프로 연결됩니다.^[32]
• 베지어 곡선의 변형감소 특성

메모들

참고문헌

인용

원천

더보기

• Bézier 곡선에 관한 기초 – 대화형 그래픽을 사용한 Bézier 곡선 및 관련 그래픽 알고리즘을 설명하는 오픈 소스 온라인 북
• Cubic Bezier Curves – Under the Hood (비디오) – 컴퓨터가 Cubic Bézier Curves를 렌더링하는 방법을 보여주는 비디오, Peter Nowell
• 미국 수학회에서 베지어에서 번스타인까지 특징 칼럼
• "Bézier curve", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Prautzsch, Hartmut; Boehm, Wolfgang; Paluszny, Marco (2002). Bézier and B-Spline Techniques. Springer Science & Business Media. ISBN 978-3-540-43761-1.
• Gallier, Jean (1999). "Chapter 5. Polynomial Curves as Bézier Curves". Curves and Surfaces in Geometric Modeling: Theory and Algorithms. Morgan Kaufmann. 이 책은 절판되어 저자가 자유롭게 이용할 수 있습니다.
• Farin, Gerald E. (2002). Curves and Surfaces for CAGD: A Practical Guide (5th ed.). Morgan Kaufmann. ISBN 978-1-55860-737-8.
• Weisstein, Eric W. "Bézier Curve". MathWorld.
• Hoffmann, Gernot. "Bézier Curves" (PDF). Archived from the original (PDF) on 2006-12-02. (60페이지)
• Ahn, Young Joon (2004). "Approximation of circular arcs and offset curves by Bézier curves of high degree". Journal of Computational and Applied Mathematics. 167 (2): 405–416. Bibcode:2004JCoAM.167..405A. doi:10.1016/j.cam.2003.10.008.
• Davies, Jason. "Animated Bézier curves".
• Hovey, Chad (20 May 2022). "Bézier Geometry". GitHub.
• Hovey, Chad (2022). 베지어와 B-스플라인 기하학의 공식화와 파이썬 구현. SAND2022-7702C. (153 pages)

외부 링크

컴퓨터코드

• 작은 스플라인: 다양한 언어에 대한 바인딩을 포함하는 NURBS, B-스플라인 및 Bézier 곡선용 오픈 소스 C-라이브러리
• 컴파일 시 Bézier 함수 생성을 위한 C++ 라이브러리
• Python에서 재귀적 방법을 통한 간단한 Bézier 곡선 구현