스피로그래프

이 글은 검증을 위해 추가 인용문이 필요합니다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 기사를 개선하는 데 도움을 주십시오. 조달되지 않은 자재는 제거될 수 있습니다.출처 : "Spirograph" – 뉴스 · 신문 · 서적 · 학자 · JSTOR (2011년 7월) (이 템플릿 메시지 삭제 방법 및 삭제 시기 확인)

스피로그래프

스피로그래프 세트(1980년대 초 영국 버전)
Inventor(들)	데니스 피셔
회사	하스브로
나라	영국
유용성	1965년 ~ 현재
자재	플라스틱
공식 웹사이트

스피로그래프는 엄밀히 말하면 빗프로코이드와 에피트로코이드로 알려진 다양한 종류의 수학적 룰렛 곡선을 만들어내는 기하학적 그리기 장치이다.잘 알려진 장난감 버전은 영국 엔지니어 데니스 피셔에 의해 개발되었고 1965년에 처음 판매되었다.

이 이름은 데니스 피셔사를 인수한 회사를 인수한 후 1998년부터 Hasbro Inc.의 등록 상표입니다.Spirograph 브랜드는 Kahootz Toys에 의해 2013년에 오리지널 제품 구성과 함께 전 세계에 다시 출시되었습니다.

역사

1827년, 그리스 태생의 영국인 건축가이자 엔지니어인 피터 휴버트 데비그네스는 정교한 소용돌이 그림을 만드는 장치인 "스피라그래프"를 개발하고 광고했다.J. Jopling이라는 이름의 남자는 곧 이전에 비슷한 ^[1]방법을 발명했다고 주장했다.1845년과 1848년 사이에 비엔나에서 일할 때, 데스비그네스는 지폐 ^[2]위조를 방지하는 데 도움이 되는 기계의 버전을 개발했습니다. 왜냐하면 그것이 만들 수 있는 거의 끝없는 룰렛 패턴의 변형들 중 어떤 것이든 되돌릴 수 있는 것은 매우 어려웠기 때문입니다.수학자 브루노 아바카노비츠는 1881년과 1900년 사이에 새로운 스피로그래프 장치를 발명했다.곡선으로 ^[3]구분된 면적을 계산하는 데 사용되었습니다.

기어에 기반한 그림 장난감은 The Sarsurous Wondergraph가 Sears ^[4][5]카탈로그에 광고된 적어도 1908년부터 존재해왔다.원더그래프 드로잉 머신을 만드는 방법을 설명하는 ^[6]기사가 1913년 소년 기계학 출판물에 실렸다.

최종 스피로그래프 장난감은 1962년부터 1964년 사이에 영국 엔지니어 데니스 피셔가 메카노 조각으로 그리기 기계를 만들어 개발했습니다.피셔는 1965년 뉘른베르크 국제 완구 박람회에 그의 스피로그래프를 전시했다.그것은 그 후 그의 회사에서 제작되었다.미국 유통권은 1966년 케너사가 미국 시장에 선보이며 창의적인 어린이 장난감으로 홍보한 것이다.케너는 나중에 스피로토, 마그네틱 스피로그래프, 스피로맨, 그리고 다양한 ^[7]리필 세트를 선보였다.

2013년 Kahootz Toys는 Spirograph 브랜드를 오리지널 기어와 휠로 전 세계에 재출시했습니다.최신 제품은 고정 부품을 고정하기 위해 핀 대신 분리 가능한 퍼티를 사용합니다.스피로그래프는 1967년 올해의^{[further explanation needed]} 장난감, 2014년 올해의 장난감으로 선정되었다.

작동

원래 미국에서 출시된 Spirograph는 크기가 다른 두 개의 플라스틱 링(또는 스테이터)으로 구성되었으며 둘레의 안쪽과 바깥쪽에 기어 톱니가 있습니다.이러한 링 중 하나를 제자리에 고정하면(핀, 접착제 또는 손으로), 제공된 여러 기어휠(또는 로터) 중 하나를 회전시켜 기하학적 모양을 그릴 수 있습니다.나중에, 슈퍼 스피로그래프는 고리, 삼각형, 그리고 직선 막대와 같은 추가 도형을 도입했다.각 조각의 모든 모서리에는 다른 조각을 결합할 수 있는 톱니가 있습니다. 작은 기어는 큰 링 안에 들어가지만 링의 바깥쪽 가장자리 또는 서로 주위를 따라 회전할 수도 있습니다.기어는 다양한 배열로 조합할 수 있습니다.세트에는 다양한 색상의 펜이 포함되어 있는 경우가 많으며, 여기에 나와 있는 예시와 같이 색을 바꿈으로써 디자인을 향상시킬 수 있습니다.

초보자들은 특히 큰 바퀴 가장자리 근처의 구멍을 사용할 때 종종 기어를 미끄러뜨려 선이 끊어지거나 불규칙하게 됩니다.경험이 풍부한 유저는, 복수의 피스(예를 들면, 링 주위의 삼각형, 링으로부터 삼각형으로 「클라이밍」하는 원)를 서로 관련지어 이동하는 것을 배울 수 있습니다.

수학적 기초

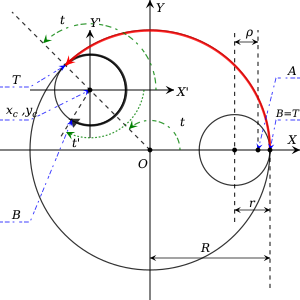
원점을 중심으로 $한{\displaystyle }$ $반지름$R의$$고정 $외측{\displaystyle {}_{}}$ 원 ${\displaystyle C_{}}$o {\$displaystyle$$C_{$o$$}}을 고려합니다.의 작은$이너서클{\displaystyle {}_{}}$ $($$디스플레이 스타일 C_{$$i$})가 Co$($스타일$C_{$o$$}) $안쪽$으로 롤링하여 연속적으로 접해 있습니다.$(실제$Spirograph에서는 양쪽 원의 톱니가 이러한 미끄러짐을 방지함) $($Co$)$에서 미끄러지지 $않는$ 것으로 간주됩니다.다음으로$$$Ci$의 내부 $어딘가$에 $있는$ $A가$$$$Ci$의$$중심에서 $거리{\displaystyle {}_{}}$ <$r$ \ displaystyle \$rho$< r$$}에 있다고 가정합니다.이 점 $(표시$ 스타일$$A)는 실제 Spirograph의 내부 디스크에 있는 펜 구멍에$$ 해당합니다.일반성을 잃지 않고 A($디스플레이 스타일$ A$)$ $지점$이 X$(디스플레이$ $스타일$ X$)$ 축에 $있었다고{\displaystyle }$ 가정할 수 있습니다.Spirograph에 의해 생성된 궤적을 찾으려면 내부 원이 움직이는 $지점{\displaystyle }$ A$(\displaystyle$ A$)$를 따릅니다.

${\displaystyle {다음}_{}}$으로 C$$$o$에 $2개$의 $포인트{\displaystyle }$ T$(디스플레이$ $스타일$ T$)$를 표시하고 ${\displaystyle {Ci}_{}}$에 B$($$디스플레이 스타일$ C_{i})에$$ B(디스플레이 스타일 C_{$i}$에 B$($디스플레이 $스타일$ B($디스플레이$ 스타일 B$)$를 표시합니다.$점{\displaystyle }$ T$(\displaystyle$ T$)$는 항상 두 원이 접하는 위치를 나타냅니다.단, $포인트{\displaystyle }$B(\$displaystyle$ B$)$는 $(\$$i$$})$로 이동하며 초기 위치는 T$(\displaystyle$ T)와$$$일치$합니다$.$Ci$(\$$displaystyle$ C_${o$})를 중심으로$$ 시계 ${\displaystyle {반대}_{}}$ ${\displaystyle {방향}_{}}$으로 이동하면 Ci$(\$ C_${$o$\})$가 회전합니다.중심부에 대한 이온.$(\$에서 B$(\displaystyle$ B$)$가 통과하는$$ 거리는 미끄러짐이 없기 때문에 $(\$의 $접점{\displaystyle }$T(\$displaystyle$ T$)$가 통과하는 거리와 동일합니다.

이제 새로운 ${\displaystyle {}^{}}({\displaystyle }$X${\displaystyle {}^{}}$, Y${\displaystyle {}^{})}$){displaystyle $(X', Y')$를 정의합니다. 원점은 $(\$의 $중심$에 있고 축은$$X(\$displaystyle$ X$)$ $및$ Y(\$displaystyle$Y$$$)$에 평행합니다. $t$는 접선 $각도$가 되도록 합니다.$\displaystyle$T는 ${\displaystyle C_{}}$ o \ $displaystyle C_{o$에서 $회전$하며 t ${\$ \ $displaystyle$ t$'$는 상대 좌표계에서 $($$\displaystyle$$C_{i$})가$$$$ $회전$하는 각도입니다.미끄러짐이 없으므로 B$($디스플레이 $스타일 B)$와 T$(디스플레이 스타일$ T$)$가 각각의 원을 따라 이동하는 거리가 같아야 합니다.

${\displaystyle tR=(t-t')r,}$

또는 동등하게

${\displaystyle t'=-{\frac {R-r}{r}}t.}$

반시계방향 운동은 양의 각도 변화에 해당하고 시계방향 운동은 음의 각도 변화에 해당한다고 가정하는 것이 일반적입니다.위의 식에서 기호( t$display$ < 0 \ $displaystyle$ $< 0$ )는 이 표기법에 대응하고 있습니다.

$({\displaystyle }$ ${\displaystyle {}_{}{c}_{}}$ , ${\displaystyle y_{}}$c$$) { $style$( x$_$ {$c$ , y$_$ { c$$} } )을$$ 절대 좌표계에서 $(\$style $C_{i$})의 중심 좌표라고 합니다.$R{\displaystyle }$- ${\displaystyle r}${\$displaystyle R-r}$은 ${\displaystyle {Ci}_{}}${\$displaystyle C_{i$의 중심 궤적의 반지름을 나타내며, 이는 (절대 시스템에서) 다음과 같이 원운동을 한다.

$\displaystyle \begin { aligned }x_{c}&=(R-r)\cos t,\y_{c}&=(R-r)\sin t.\end { aligned}}$

위에서 정의한 바와 같이 t ${\$ {$displaystyle$ t$'$는 새로운 상대 시스템의 회전 각도입니다.$점{\displaystyle }$ A$(\displaystyle$ A$)$는 일반적인 원형 운동 법칙을 따르므로 새로운 상대 좌표계$x$(, y$))$의 $좌표계$는 다음과 같습니다.

$cos t, y'=\rho t'입니다.\end { aligned}}$

절대 좌표계에서$$A(\$displaystyle$ A$)$의 궤적을 얻으려면 다음 두 가지 동작을 추가합니다.

${\displaystyle {begin}x&=x_{c}+x'=(R-r)\cos t+\rho \cos t',\y&=y_{c}+y'=(R-r)\sin t+\rho \sin t',\end {align t}$

여기서 $"\displaystyle\rho"$는 위에 정의되어 있습니다.

$위$의 t$\displaystyle$t와$$ $t{\displaystyle {}^{}}$ ${\\$t'의 $관계$를 사용하여$단일{\displaystyle }$ $파라미터$ t\$displaystyle$t로$점$ A의 궤적을 기술하는 방정식을 구합니다.

${\displaystyle {begin}x&=x_{c}+x'=(R-r)\cos t+\rho \cos {frac {R-r}{r}t,\y&=y_{c}+y'=(R-r)\rho \sin {r}\endalign {r}t}\cos t$

(${\displaystyle \mathrm{함수}}$$sin$이 이상하다는 사실을 사용$).$

위의 방정식은 ${\displaystyle {Co}_{}}$의$$$반지름{\displaystyle }$R({$displaystyle$$$$C_{o$})과$$$$ Spirograph의 구조를 설명하는 무차원 파라미터로 표현하면 편리합니다.즉,

${\displaystyle l=black{rho}{r}}$

그리고.

${\displaystyle k=syslogfrac {r}{R}}$

$파라미터{\displaystyle \mathrm{}}$ 0${\displaystyle l}$ l${\displaystyle 1}$1 { $displaystyle$0 \$leq$ l \$leq$ 1$$}는 점 A가$$${\displaystyle {Ci}_{}}$(\$displaystyle C_{i$의 중심에서 얼마나 떨어져 있는지를 나타냅니다$$.또한 0${\displaystyle k}$ k$$1 { $displaystyle$0 \ $leq$ 1$$}은 내부 $Ci$(\displaystyleq C$)$의 크기를 나타냅니다$$.외부 C$$(\$displaystyle C_{o$

라는 것이 현재 관측되고 있다.

$(\displaystyle\frac{rho}{R}}=lk,}$

따라서 궤적 방정식은 그 형태를 취한다.

$({displaystyle {begin{aligned}x(t)&=R\left[(1-k)\cos t+lk\cos {frac {1-k}{k}t\right],\y(t)&=R\left[(1-k)\sin t-lk}\sin {k}\right}).\\\end {aligned}}$

$파라미터{\displaystyle }$ R$(\displaystyle$ R$)$은 스케일링 파라미터이며 Spirograph의 구조에는 영향을 주지 않습니다.R$(\displaystyle$ R$)$의 값이 다르면 유사한 Spirograph 도면이 생성됩니다.

극단적인 $경우{\displaystyle }$ k ${\displaystyle =}$ {$displaystyle$ k$=0}$ 및$$ $k{\displaystyle }$ ${\displaystyle =}$ {$displaystyle$ k$=1$}$$두 개가 Spirograph의 궤적을 저하시킵니다.첫 번째 극단적인 경우 k ${\displaystyle =}$ $(\displaystyle$ k$=0$일 때,$$(\$displaystyle C_{$i$$})가 점으로 축소된 경우에 대응하는 단순한 $반지름{\displaystyle }$R(\$displaystyle$ R$)$의 원이 있습니다.(식 중 k ${\displaystyle =}$(\$displaystyle$$$k$=0)$로 나눗셈하는 것은 ${\displaystyle \mathrm{문제}}$가 $되지$ 않습니다$.)$$n }$ ${\displaystyle \mathrm{및<img\; alt="\backslash sin\; "\; aria-hidden="true"\; class="mwe-math-fallback-image-inline"\; src="https://wikimedia.org/api/rest\_v1/media/math/render/svg/ee55beec18afd710e7ab767964b915b020c65093"\; style="vertical-align:\; -0.338ex;\; width:2.856ex;\; height:2.176ex;">}}$cos {\$displaystyle \cos}$는 경계 함수입니다.

다른 극단적인 $경우{\displaystyle }$ k ${\displaystyle =}$ ${\displaystyle 1}${$style$ k=1}은 $외부$원 C의 ${\displaystyle {반지름}_{}}$$R{\displaystyle }$$$$o$ {\$displaystyle$C_${$o}과$($$와$) 일치하는 내부 ${\displaystyle {원}_{}}$ $C{\displaystyle {}_{}}$i {\$displaystyle$ R$}$의 반지름$$r {\$displaystyle$ r$}$에 해당합니다$$. 즉, $단일{\displaystyle }$ 궤적에서는 r ${\displaystyle =}$ {\$displaystyle$ R $=$ R }입니다.포인트. 직감적으로 $Ci는$ 커서 같은 $사이즈$의 $(\$ C_${o})$ 안에서$$$$ 미끄러지지 않고 굴릴 수 없습니다.

l ${\displaystyle =}$ $({displaystyle$ l$=1$인 $,$ A({$displaystyle$ A$})$$$지점은 ${\displaystyle {Ci}_{}}$(\$displaystyle C_{i$의 둘레에 있습니다.이 경우, 이 궤적을 하이포사이클로이드라고 하며 위의 방정식은 하이포사이클로이드라고 합니다.

「 」를 참조해 주세요.

레퍼런스

외부 링크

• 공식 웹사이트
• Voevudko, A. E. (12 March 2018). "Gearographic Curves". Code Project.