흉부외과

심근경색체(그리스어 καρΔα "심장"에서)는 같은 반지름의 고정된 원을 둘레에 구르고 있는 원의 둘레에 있는 한 점에 의해 추적되는 평면 곡선이다. 그것은 또한 하나의 정지를 가진 에피시클로이드로 정의될 수 있다. 또한 정현곡선의 일종으로 포커스를 역방향의 중심으로 포물선의 역곡선이다.^[1] 또한 원의 모든 접선을 통해 원의 고정점을 반사하는 점들의 집합이기도 하다.^[2]

이 이름은 1741년^[3] 드 카스틸론에 의해 만들어졌지만 수십 년 전부터 연구 대상이 되어 왔다.^[4] 하트모양이라고 이름 붙여진 그것은 줄기가 없는 둥근 사과의 단면 윤곽처럼 생겼다.

심근경색 마이크로폰은 2차원으로 그래프를 그릴 때 심근경색(마이크 본체의 3d 직선을 포함하는 모든 2d 평면)과 유사한 음향 픽업 패턴을 보인다. 3차원에서는, 심근경색은 사과의 "stalk"인 마이크를 중심으로 사과 모양을 하고 있다.

방정식

$중간점$$({\displaystyle }$-$$${\displaystyle a}$, ${\displaystyle 0}$)${\displaystyle }$,${\displaystyle }$(${\displaystyle }$, ${\displaystyle 0}$) ${\displaystyle(-a,0),$ ($a,0)$ ,$$$\phi {\displaystyle }$ ${\displaystyle \varphi},$ 롤링$$ 각도 및 원점(그림 참조)을 가진 두 생성 원의 공통 반지름이 되도록$$ 한다$.$ 한 사람이 그 일을 맡다.

• 모수 표현:

${\displaystyle x(\varphi )=2a(1-\cos \varphi )\cdot \cos \varphi \,}$

${\displaystyle y(\varphi )=2a(1-\cos \varphi )\cdot \sin \varphi \\\qquad 0\leq \varphi <2\pi }}$

그리고 여기서부터.

• 극좌표:

${\displaystyle r}$ (${\displaystyle \phi }$ )${\displaystyle }$= ${\displaystyle 2}$ ${\displaystyle \mathrm{a}}$( 1${\displaystyle }$- ${\displaystyle \cos }$ ${\displaystyle }$ ${\displaystyle \phi }$) ${\displaystyle r(\varphi )=2a(1-\cos \varphi )}$.

대체 ${\displaystyle \cos }$ 소개${\displaystyle \mathrm{introducing}}$= ${\displaystyle x}$/ ${\displaystyle r}$ ${\displaystyle \cos \varphi =x/r}$ 및 $r$ = ${\displaystyle \sqrt{{x\mathrm{}}^{}}}$ 2${\displaystyle \sqrt{{}^{}}}$+ ${\displaystyle \sqrt{{}^{}}}$ ${\displaystyle \sqrt{{2\mathrm{}}^{}}}$ ${\$ r$={\sqrt {x^{2}+y^{2$}$}}}}$ 제곱근을$$ 제거한 후 암묵적 표현을 얻음

• 데카르트 좌표:

${\displaystyle (}$ ${\displaystyle {x\mathrm{}}^{}}$ 2${\displaystyle {}^{}}$+ ${\displaystyle {y\mathrm{}}^{}}$ ${\displaystyle {}^{}{}^{}}$) ${\displaystyle {2\mathrm{}}^{}}$+ ${\displaystyle a}$ ${\displaystyle x}$ (${\displaystyle {}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$+ y ${\displaystyle {2\mathrm{}}^{}}$)${\displaystyle }$- ${\displaystyle {4\mathrm{}}^{}}$ a ${\displaystyle {2\mathrm{}}^{}{}^{}}$= ${\displaystyle 0\mathrm{}}$ ${\displaystyle (x^{2}+y^{2})^{2}+4ax(x^{2}+y^{2})-4a^{2}{2}\,=\,0}$ $$.

모수 표현에 대한 증거

복잡한 숫자와 복잡한 평면으로서의 공통적인 설명을 사용하여 증거를 확립할 수 있다. 파란색 원 위에 있는 검은 원의 구르는 동작은 두 개의 회전으로 나눌 수 있다. 복합 평면에서는 점 $0{\displaystyle \mathrm{}}$ ${\displaystyle$ 0$}($원점)을 각도 $\phi {\displaystyle }$ ${\displaystyle \varphi }$에 점 $z{\displaystyle }$ ${\displaystyle$ z$}($복수 번호)를 $e{\displaystyle {}^{}}$ ${\displaystyle {\phi }^{}}$ ${\$에 곱하여 회전할 수 있다$$$.$

$\$ + {\$displaystyle a}$ 지점 $주위$의 $회전{\displaystyle {\mathrm{}}_{}}$ $\Phi _{+}$는 ${\displaystyle }$ z ${\displaystyle z}$ a${\displaystyle }$+ (${\displaystyle z}$- ${\displaystyle a}$) ${\displaystyle e}$i ${\displaystyle i^{}}$ ${\$ $\}\}\}\},$

$rotation{\displaystyle {\mathrm{}}_{}}$- ${\$ 지점 ${\displaystyle \mathrm{주변<img\; alt="\{\backslash displaystyle\; \backslash Phi\; \_\{-\}\}"\; aria-hidden="true"\; class="mwe-math-fallback-image-inline"\; src="https://wikimedia.org/api/rest\_v1/media/math/render/svg/31c3c04196a4ea1b5e47798205cbf36c6e15d0e1"\; style="vertical-align:\; -0.671ex;\; width:3.189ex;\; height:2.509ex;"\; papago-attr-id="74">}}$ -${\displaystyle -a}$은(는) $z{\displaystyle }$ -${\displaystyle }$a ${\displaystyle +}$ ${\displaystyle (z}$+ ${\displaystyle a)}$ ${\displaystyle {}^{}}$ ${\displaystyle i^{}}$ ${\displaystyle {\phi }^{}}$ ${\$ z\$mapsto -a+(z+a)^{i\varphi$ $\}\}\}.$

심근경색증의 $p$ (${\displaystyle \phi }$) ${\displaystyle$ p$(\$$varphi$ $)}$은(는) 원점을 ${\displaystyle a}$ 지점 $중심$으로 회전한 후$$ 동일한 각도 $\phi {\displaystyle }$ ${\displaystyle$$-a}$을(는$)$ 회전시켜 생성된다$.$

${\displaystyle p(\varphi )=\Phi _{-}(\Phi _{+}(0))$$=\Phi _{-}(a-ae^{i\varphi }}}=-a+(a-ae^{i\varphi }a)={i\varphi }=a\(-e^{i2\varphi }+2e^{i\varphi }-1$

여기서부터는 위의 파라메트릭 표현을 얻는다.

${\displaystyle {\begin{array}{cclcccc}x(\varphi )&=&a\;(-\cos(2\varphi )+2\cos \varphi -1)&=&2a(1-\cos \varphi )\cdot \cos \varphi &&\\y(\varphi )&=&a\;(-\sin(2\varphi )+2\sin \varphi )&=&2a(1-\cos \varphi )\cdot \sin \varphi &.&\end{array}}}$

(The formulae ${\displaystyle e^{i\varphi }=\cos \varphi +i\sin \varphi ,\ (\cos \varphi )^{2}+(\sin \varphi )^{2}=1,\ \cos 2\varphi =(\cos \varphi )^{2}-(\sin \varphi )^{2},\;\sin$$2\varphi =2\sin \varphi \cos \varphi }$이(가) 사용되었다$$. 삼각함수를 참조하십시오.)

메트릭 속성

위에서 정의한 흉부외과의 경우 다음 수식을 유지하십시오.

• 영역 $A{\displaystyle }$= ${\displaystyle 6}$ ${\displaystyle \pi }$ ${\displaystyle {}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$ ${\$ a$^{2$
• 호$$ 길이 $L{\displaystyle }$= ${\displaystyle \mathrm{16}}$ a ${\displaystyle L=16a}$ 및
• 곡률 반경 ${\displaystyle \rho (\varphi )={\tfrac {8}{3}a\sin {\tfrac {\barphi }{2}}\ .}$

이 진술의 증거는 두 경우 모두 흉부외과의 극지방 표현을 사용한다. 적절한 수식은 극좌표계(arc 길이) 및 극좌표계(면적)를 참조하십시오.

면적 공식의 증명

${\displaystyle A=2\cdot {\tfrac {1}{2}}\int _{0}^{\pi }{(r(\varphi ))^{2}}\;d\varphi =\int _{0}^{\pi }{4a^{2}(1-\cos \varphi )^{2}}\;d\varphi =\cdots =4a^{2}\cdot {\tfrac {3}{2}}\pi =6\pi a^{2$$}}$ .

호 길이 공식의 증명

${\displaystyle L=2\int _{0}^{\pi }{\sqrt {r(\varphi )^{2}+(r'(\varphi ))^{2}}}\;d\varphi =\cdots =8a\int _{0}^{\pi }{\sqrt {{\tfrac {1}{2}}(1-\cos \varphi )}}\;d\varphi =8a\$$int _{0}^{\pi }\sinsin\tfrac {\varphi }{2}})d\varphi =16a}$ $$.

곡률 반경에 대한 증거

등식 $r{\displaystyle }$= ${\displaystyle r}$ (${\displaystyle \phi }$) ${\displaystyle \rho$ $}$이$(가$) 있는 극좌표 곡선의 곡면 $반경$은 (s. 곡률)이다$$.

${\displaystyle \rho (\varphi )={\frac {\left[r(\varphi )^{2}+{\dot {r}}(\varphi )^{2}\right]^{3/2}}{r(\varphi )^{2}+2{\dot {r}}(\varphi )^{2}-r(\varphi ){\ddot {r}}(\varphi )}}\ .}$

흉부외과적 $r{\displaystyle }$(${\displaystyle \mathrm{\phi }}$)${\displaystyle }$= ${\displaystyle 2}$ a (${\displaystyle }$1${\displaystyle }$- ${\displaystyle \cos }$ ${\displaystyle }$ ⁡${\displaystyle }$)${\displaystyle }$= ${\displaystyle 4}$ ${\displaystyle {\sin }^{}}$ 2$$φ ${\displaystyle \phi \frac{}{}}$ ${\displaystyle \frac{2}{}}$ {\$displaystyle$r(\$varphi )=2a(1-$\cos $\varphi$)=$4a\$sin$^{2$}{\$tfrac {\varphi }{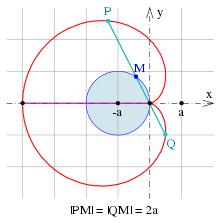2$$}}:$

${\displaystyle \rho (\varphi )=\cdots ={\frac {[16a^{2}\sin ^{2}{\frac {\varphi }{2}}]^{\frac {3}{2}}}{24a^{2}\sin ^{2}{\frac {\varphi }{2}}}}={\frac {8}{3}}a\sin {\frac {\varphi }{2}}\ .}$

특성.

정지를 통과하는 화음

• C1: 심장의 정지를 통과하는 화음의 길이는 같은 $4{\displaystyle \mathrm{}}$ a ${\displaystyle 4a}$이다.$$
• C2: 정지를 통과하는 화음의 중간점은 고정 발전기 원의 둘레에 있다(그림 참조).

C1의 교정쇄.

$P{\displaystyle }$: ${\displaystyle p}$ (${\displaystyle \phi }$ )${\displaystyle }$, ${\displaystyle Q}$: ${\displaystyle p}$ (${\displaystyle \phi }$+ ${\displaystyle \pi }$) ${\displaystyle P:p(\varphi "),\;Q:p(\varphi +\pi )}}$ 포인트는 cusp(=origin)를 통해 화음에 있다$$. 그러므로

${\displaystyle PQ =r(\varphi )+r(\varphi +\pi )}$

${\displaystyle =}$ 2 ${\displaystyle a}$( ${\displaystyle 1}$- ${\displaystyle \cos }$ ${\displaystyle \phi }$ )${\displaystyle }$+ ${\displaystyle 2}$ ${\displaystyle \mathrm{a}}$( ${\displaystyle 1}$- ${\displaystyle \cos }$ ${\displaystyle }$ (${\displaystyle +}$ + ${\displaystyle )}$)${\displaystyle }$=$$= ${\displaystyle 4}$ a ($1-\cos \varphi )+2a (1-\cos(\varphi +\pi )=\cdots =4a}.$

C2용 교정쇄

증거를 위해 복합 평면에서의 표현(위 참조)을 사용한다. 포인트로

${\displaystyle P:\ p(\varphi )=a\;(-e^{i2\varphi }+2e^{i\varphi }-1)}$

${\displaystyle Q:\ p(\varphi +\pi )=a\;(-e^{i2(\varphi +\pi )}+2e^{i(\varphi +\pi )}-1)=a\;(-e^{i2\varphi }-2e^{i\varphi }-1)}$,

$현{\displaystyle }$ P ${\displaystyle Q}$ ${\displaystyle PQ}$의 중간점은

${\displaystyle M:\\\tfrac {1}{1}:{2}}(p(\varphi )+p(\varphi +\pi )=\cdots =-a-ae^{i2\varphi }}}}}}}}}}$

중간 지점$({\displaystyle -a})$과 반지름 $a{\displaystyle }$ ${\displaystyle a}($사진 참조)로 원의 둘레에 놓여 있다.$$

포물선 역곡선으로서의 심근경색

• 심근경색(cardioid)은 포물선의 초점이 반전 중심에 있는 포물선의 역 곡선이다(그래프 참조).

그래프에 표시된 예제의 경우 제너레이터 원의 $반지름$은 a${\displaystyle }$= ${\displaystyle \frac{1}{}}$ 2 ${\$ 따라서 심근경색증은 극성을 나타낸다.

${\displaystyle r(\varphi )=1-\cos \varphi }$

그리고 그 역곡선

${\displaystyle r}$ (${\displaystyle \phi }$ )${\displaystyle }$= ${\displaystyle \frac{1\mathrm{}}{}}$ -${\displaystyle \frac{\cos }{}}$ ${\displaystyle \frac{}{}}$ ${\$ {1$}{1-\cos \varphi$ $\}\},$

포물선(극좌표에서는 s. 포물선)이며, 데카르트 좌표에서는$$ $x{\displaystyle }$= ${\displaystyle \frac{1}{}}$ 2 ${\displaystyle ({}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$- ${\displaystyle 1}$)$${\$displaystyle x={\tfrac{1}{2}}(y^{2$}-$1)}$ 등식이 있다.

비고: 포물선의 모든 역 곡선이 심근경색인 것은 아니다. 예를 들어 포물선의 정점에 중심이 놓여 있는 원을 가로질러 포물선이 반전되면 그 결과는 디오클레스의 시스소이드(cissoid)가 된다.

동그라미 연필 봉투처럼 심근 강화제

앞의 절에서 포물선의 접선을 추가로 반전시키면 반전 중심(원점)을 통해 원의 연필을 얻는다. 상세한 고려사항은 다음과 같다. 원의 중간점은 고정 발전기 원의 둘레에 있다. (발전기 원은 파라볼라 다이렉트릭스의 역곡선이다.)

이 특성은 다음과 같은 간단한 흉부외과를 그리는 방법을 만들어 낸다.

1) $둘레$에$$있는 원 c {\$displaystyle$ $c}$와 점 $O{\displaystyle }$ ${\displaystyle$ O$}$을(를) 선택하십시오.

2) $c{\displaystyle }$ ${\displaystyle c}$에 $중심$이 있는$$ O ${\displaystyle O}$을(를) 포함하는 원을 그리십시오$.$

3) 이 원들의 봉투를 그려라

봉투 조건을 붙여서 증명하다.

암시적으로 지정된 곡선의 연필 봉투

$F(x,y,t)=0}$

매개 변수 $t{\displaystyle }$ ${\displaystyle$ t$}$은(는) 비선형 시스템의 솔루션인${\displaystyle }$(${\displaystyle x}$, ${\displaystyle y}$) ${\displaystyle (x,y)}$과(와) 같은 점으로 구성된다$$.

• ${\displaystyle F(x,}$ ${\displaystyle y,}$ t${\displaystyle }$)${\displaystyle }$= ${\displaystyle 0,}$ ${\displaystyle F{}_{}}$ ${\displaystyle t_{}x,}$ y${\displaystyle ,}$ ${\displaystyle t}$)${\displaystyle }$= ${\displaystyle 0}$ ${\$진행 조건).

(${\displaystyle {}_{}}$ ${\displaystyle t_{}}$ ${\$는 매개변수 t$${\$displaystyle t}$에 대한 부분파생물을 의미한다$.$

$c{\displaystyle }$ ${\displaystyle c}$을(를${\displaystyle )}$ 중간점$({\displaystyle }$- ${\displaystyle 1}$, 0${\displaystyle }$) ${\displaystyle(-1,0)$과 $반지름{\displaystyle \mathrm{}}$ 1 ${\displaystyle$ $c$$}$을(를${\displaystyle )}$ 가진 원으로$$ 두십시오$.$ 그러면 $c{\displaystyle }$ ${\$$displaystyle$ c$}$에는 ${\displaystyle \mathrm{파라메트릭}}$ ${\displaystyle \mathrm{표현}(}$ - 1${\displaystyle }$+ ${\displaystyle \cos }$ t${\displaystyle ,}$ sin$$$\$ t ) {$1+\cos t$ t${\displaystyle )}$이 있습니다$$. $점$ $O{\displaystyle }$=${\displaystyle }$( 0${\displaystyle }$,$0$)을 포함하는$$ $c{\displaystyle }$ ${\$$displaystyle$ $c}$에 중심이 있는 원의 연필은 다음과 같이 암시적으로 나타낼 수 있다$$$.$

${\displaystyle F}$( ${\displaystyle x}$, ${\displaystyle y}$, ${\displaystyle t}$)${\displaystyle }$=${\displaystyle }$( ${\displaystyle \mathrm{x}}$+ 1${\displaystyle }$- ${\displaystyle \cos }$ ${\displaystyle }$ ${\displaystyle t{}^{}}$) ${\displaystyle {2\mathrm{}}^{}{}^{}}$+${\displaystyle }$( ${\displaystyle y}$- ${\displaystyle \sin }$ ${\displaystyle }$ ${\displaystyle t{}^{}}$) 2${\displaystyle {}^{}}$-${\displaystyle }$( 2${\displaystyle }$- 2 ${\displaystyle \cos }$ ${\displaystyle }$ ${\displaystyle t}$)${\displaystyle }$= ${\displaystyle 0}$ ${\displaystyle F(x,y,t)=(x+1-\cos$ t$)^{2}-(y-\sin$ t$)^{2-2-\cos t=0$ ,,

에 해당하는

${\displaystyle F(x,y,t)=x^{2}+y^{2}+2x\;(1-\cos t)-2y\;\sin t=0\;.}$

두 번째 봉투 조건은

${\displaystyle F_{}}$ ${\displaystyle t_{}}$( ${\displaystyle x}$, ${\displaystyle y}$, t${\displaystyle }$)${\displaystyle }$= ${\displaystyle 2}$ x ${\displaystyle \sin }$ ${\displaystyle }$ t${\displaystyle }$- ${\displaystyle 2}$ ${\displaystyle \mathrm{y}}$ ${\displaystyle \cos }$ ${\displaystyle \cos }$t${\displaystyle }$= ${\displaystyle 0}$ ${\displaystyle F_{t}(x,y,t)=2x\;\sin t-2y\;\cos t=0$ .

파라메트릭을 가진 흉부외과의 포인트를 쉽게 확인할 수 있다.

${\displaystyle x(t)=2(1-\cos t)\cos t,\cos t,\cos y(t)=2(1-\cos t)\sin t}$

위의 비선형 체계를 충족시키다 매개 $변수{\displaystyle }$ t$${\$displaystyle t$}은(는) 심근경색의 각도 매개 변수와 동일하다$$.

선필봉투를 이용한 심근 강화제

흉부외과를 그리는 유사하고 간단한 방법은 선 연필을 사용한다. 그것은 L. Cremona 때문이다:

1. 원을 그리고 둘레를 ${\displaystyle \mathrm{2N}}$ ${\displaystyle 2N}$ 포인트$$(s. picture)가 있는 동일한 간격으로 나눈 다음 연속적으로 번호를 매긴다.
2. Draw the chords: ${\displaystyle (1,2),(2,4),....,(n,2n),....,(N,2N),(N+1,2),(N+2,4),....,}$. (i.e.: 두 번째 점은 이중 속도로 이동한다.)
3. 이 화음의 봉투는 심근경색이다.

증빙의

The following consideration uses trigonometric formulae for ${\displaystyle \cos \alpha +\cos \beta ,\ \sin \alpha +\sin \beta ,\ 1+\cos 2\alpha ,\ \cos 2\alpha ,\sin 2\alpha }$. In order to keep the calculations simple, the proof is given for the cardioid with 극지방 $표현{\displaystyle }$ ${\displaystyle \mathrm{r}}$= ${\displaystyle 2}$( 1${\displaystyle }$+ ${\displaystyle \cos }$ ${\displaystyle }$ ${\displaystyle \phi }$) ${\displaystyle r=2(1{\color {red}+}\cos \varphi )}($다른 위치의 Cardioids 섹션 참조).

접선 방정식

극지방 표현 $r{\displaystyle }$= ${\displaystyle 2}$ (${\displaystyle 1}$+ ${\displaystyle \cos }$ ${\displaystyle }$) ${\displaystyle r=2(1+\cos \varphi )}$:

모수 표현에서

${\displaystyle x(\varphi )=2(1+\cos \varphi )\cos \varphi ,}$

${\displaystyle y(\varphi )=2(1+\cos \varphi )\sin \varphi }$

정상 벡터 $n{\displaystyle \stackrel{}{}}$→${\displaystyle }$=${\displaystyle }$(${\displaystyle y\stackrel{}{}}$ ${\displaystyle \stackrel{}{\dot{}}}$,${\displaystyle }$- ${\displaystyle x\stackrel{}{}}$ ${\displaystyle \stackrel{}{\dot{}}{}^{}}$) ${\displaystyle T^{}}$ ${\$${T}}$. The equation of the tangent ${\displaystyle {\dot {y}}(\varphi )\cdot (x-x(\varphi ))-{\dot {x}}(\varphi )\cdot (y-y(\varphi ))=0}$ is:

$#\displaystyle(\cos 2\varphi +\cos \varphi )\cdot x\+\(\sin 2\varphi +\sin \varphi )\cdot y=2(1+\cos \varphi )^{2}\}$

trigonometric 공식과 cos cos ${\displaystyle 1\frac{2}{}}$ ${\displaystyle \phi }$ ${\displaystyle \cos {\tfrac {1}{1}:{$2}}\$varphi}}$에 의한 후속 분리의 도움을 받아 접선 방정식을 다음과 같이 다시 쓸 수 있다$.$

• ${\displaystyle \cos({\tfrac {3}{2}\varpi )\cdot x+\sinfrac\tfrac {3}\cos {1}{1}{2}}\varphi )^{3}\barphi <2\pi\varphi \q \pi}.$

화음의 방정식

of the circle with midpoint ${\displaystyle (1,0)}$ and radius ${\displaystyle 3}$: For the equation of the secant line passing the two points ${\displaystyle (1+3\cos \theta ,3\sin \theta ),\ (1+3\cos {\color {red}2}\theta ,3\sin {\color {re$$d}2}\theta )}$개$$:

$#\displaystyle(\sin \theta -\sin 2\theta )\cdot x\+\(\cos 2\theta -\sin \cdot y=-2\cos \theta -\sin 2\theta \}$

삼각법 공식과 ${\displaystyle \sin \frac{\mathrm{\theta }}{}}$ 1 2$$ {\$displaystyle \$sin {\$tfrac$ {1$}{1$}:{2$}}\teta}$에 의한 후속 분할의 도움을 받아 secant 라인의 방정식을$$ 다음과 같이 다시 쓸 수 있다.

• ${\displaystyle \cos({\tfrac {3}{2}\theta )\cdot x+\sinfrac\tfrac {3}\cdot y=4(\cos {1}{1}{2}}\tea )^{3}\capta <2\pi .}$

두 $각도{\displaystyle }$ ${\displaystyle ,\mathrm{에도}}$ 불구하고, { ${\$$displaystyle$ $\$$varphi ,\teta }$은 같은$$ ${\displaystyle 선}$에 대해 얻는 의미(s$.$ picture)가 다르다$$${\displaystyle .}$ 따라서 위에서 정의한 원의 모든 세컨트 라인은 심근경색의 접선이기도 하다.

• 흉부외과는 원의 화음의 봉투다.

비고:
증거는 곡선의 암시적 연필의 봉투 조건(이전 절 참조)의 도움을 받아 수행할 수 있다.

${\displaystyle F(x,y,t)=\cos {\tfrac {3}{2}}t\cdot x\ +\ \sin {\tfrac {3}{2}}t\cdot y-4(\cos {\tfrac {1}{2}}t)^{3}=0\ }$ is the pencil of secant lines of a circle (s. above) and

${\displaystyle F_{t}(x,y,t)=-{\tfrac {3}{2}}\sin {\tfrac {3}{2}}t\cdot x\ +\ {\tfrac {3}{2}}\cos {\tfrac {3}{2}}t\cdot y+3\cos {\tfrac {1}{2}}t\sin t=0\ .}$

고정 매개변수 t의 경우 두 방정식은 모두 선을 나타낸다. 그들의 교차점은

${\displaystyle x}$( ${\displaystyle t}$)${\displaystyle }$= ${\displaystyle 2}$( 1${\displaystyle }$+ ${\displaystyle \cos }$ ${\displaystyle }$ ${\displaystyle t}$) ${\displaystyle \cos }$ ${\displaystyle }$ ${\displaystyle t}$, y${\displaystyle }$( t${\displaystyle }$)${\displaystyle }$= ${\displaystyle 2}$( ${\displaystyle 1}$+ ${\displaystyle \cos }$ ${\displaystyle }$ t${\displaystyle }$) ${\displaystyle \sin }$ (${\displaystyle }$) sin t ) sin$sin$ t {\$displaysty x(t)=2 (1+\cos t)\cos t$

극성 방정식 ${\displaystyle \mathrm{r}}$= 2${\displaystyle }$( 1${\displaystyle }$+ ${\displaystyle \cos }$ ${\displaystyle }$ ${\displaystyle t}$) .${\displaystyle r=2 (1+\cos$ t)를 가진 심근경색 지점이다$.$$}$

동그라미 가성인 흉부외과

앞 절에서 고려한 사항은 원의 둘레에 광원이 있는 원의 가성비가 심근경색이라는 증거를 제시한다.

• 평면 내에 어떤 광선을 반사하는 원의 둘레에 있는$$ $Z{\displaystyle }$ ${\displaystyle Z}$ 지점에 광원이 있는 경우, 원 내의 반사 광선은 흉부외막의 접선이다.

증빙의

이전 섹션에서와 같이 원이 중간점$({\displaystyle 1}$, 0${\displaystyle }$) ${\$디스플레이 $스타일(1,0)}$ 및 반지름$$ $3{\displaystyle \mathrm{}}$ ${\디스플레이$ 스타일 $3}$을(를) 가질 수 있다$.$ 그 파라메트릭 표현은 다음과 같다.

${\displaystyle c(\varphi )=(1+3\cos \varphi ,3\sin \varphi )\ .}$

The tangent at circle point ${\displaystyle C:\ k(\varphi )}$ has normal vector ${\displaystyle {\vec {n}}_{t}=(\cos \varphi ,\sin \varphi )^{T}}$. Hence the reflected ray has the normal vector ${\di$$splaystyle {\vec {n}}_{r}=(\cos {\color {red}{\tfrac {3}{2}}}\varphi ,\sin {\color {red}{\tfrac {3}{2}}}\varphi )^{T}}$ (see graph) and contains point ${\displaystyle C:\ (1+3\cos \varphi ,3\sin \varphi )}$. 반사 광선은 등식이 있는 선의 일부임(이전 섹션 참조)

${\displaystyle \cos{\tfrac {3}{2}}\varphi \cdot x\+\\sin {\tfrac {3}{3}\cdot y=4(\cos {1}{1}{2}}\barphi )^{3}\},},}$

극성방정식을 가진 심근경색의 탄젠트.

${\displaystyle r=2(1+\cos \varphi )}$

전편에서

비고: 그러한 고려사항으로 인해 일반적으로 원의 다중 성찰은 무시된다.

원의 페달 곡선으로 심근경색

심근경화증의 크레모나 세대는 다음 세대와 혼동해서는 안 된다.

이$$ 원의 둘레에 $있는{\displaystyle }$ $K{\displaystyle }$$${\$displaystyle k}$와 O ${\displaystyle$ O$}$을(를) 점으로$$ 한다. 다음은 사실이다.

• 원 $k{\displaystyle }$ ${\displaystyle k}$의 $접선$에 있는$$ O$${\$displaystyle O}$ 지점에서 수직으로 된 발은 심근경색의 지점이다$$.

그래서 심근경색은 원의 특별한 페달 곡선이다.

증빙의

데카르트 좌표계 원 $k{\displaystyle }$ ${\displaystyle k}$에서 중간점$({\displaystyle 2}$ ${\displaystyle a}$, ${\displaystyle 0}$) ${\displaystyle(2a,0)$ 및$$ 반지름 2 ${\displaystyle a}$ ${\displaystyle 2a}$을(를) 가질 수 있다$$$.$ 원 포인트의 접선${\displaystyle }$(${\displaystyle 2}$ a${\displaystyle }$+ ${\displaystyle \mathrm{a}}$ ${\displaystyle \cos }$ ${\displaystyle ,2}$ ${\displaystyle a}$ ${\displaystyle \sin }$ ${\displaystyle \phi }$ ) ${\displaystyle (2a+2a\cos \varphi$ ,$2a\sin \varphi )}$에는 방정식이 있다$$.

$\displaystyle (x-2a)\cdot \cdot \varphi +y\cdot \sin \varphi =2a\ .}$

접선의 $O$ ${\displaystyle O}$ 지점에서 수직인 발은 점(${\displaystyle r}$ ${\displaystyle \cos }$ cos${\displaystyle \phi ,}$ ${\displaystyle r}$ ${\displaystyle \sin \sin }$) ${\displaystyle(r$$\cos$ $\varphi,r\sin \varphi$)이며$$, 원점 $O{\displaystyle }$ ${\displaystyle$ O$}$까지의 $거리$는 여전히 알 수 없다$.$

${\displaystyle(r\cos \varphi -2a)\cos \varphi +r\sin ^{2}\varphi =2a\prow \rightarrow \r=2a(1+\cos \varphi )}$

심근 강화제의 극성 방정식이지

비고: 점 $O{\displaystyle }$ ${\displaystyle O}$이(가) 원 k ${\displaystyle k}$의 둘레에 있지$$ 않으면$$Pascal의 리마손이 생긴다.

흉부외과의 퇴치

곡선의 이탈은 곡률의 중심점이다. 자세한 내용: $곡률{\displaystyle \stackrel{}{}}$ 반경이 ${\displaystyle \rho }$( ${\displaystyle )\{\backslash }$$displaystyle {\vec{x}}={\vec{c}}}}$인 곡선 x${\displaystyle \stackrel{}{}}$→${\displaystyle }$(${\displaystyle s}$) =${\displaystyle \stackrel{}{}c\stackrel{}{}}$= ($s$ ${\displaystyle \rho(s)}$의 경우 절대값이$$ 표현된다.

${\displaystyle {\vec{X}={\vec}}+\rho(s){\vec{n}}s.}$

$n{\displaystyle \stackrel{}{}}$→${\displaystyle }$( $){\displaystyle{\vec{n}}}}$의 적절한 방향의 장치 정상.

흉부외과의 경우:

• 심근경색증을 없애는 것은 또 다른 심근경색증이다.

증빙의

파라메트릭 표현을 사용하는 심근경색인 경우

${\displaystyle x(\varphi )=2a(1-\cos \varphi )\cos \varphi =4a\sin ^{2}{\tfrac {\varphi }}cos \varphi \},}$

${\displaystyle y(\varphi )=2a(1-\cos \varphi )\sin \varphi =4a\sin ^{2}{\tfrac{}{2}}\sin \varphi }}}$

단위 보통은

${\displaystyle {\vec{n}(\varphi )=(-\sin {\tfrac {3}{2}}\varphi ,\cos {\tfrac {3}{2}}\varphi )}}$

곡률 반경

${\displaystyle \rho (\varphi )={\tfrac {8}{3}a\sin {\tfrac {\barphi }{2}}\ .}$

따라서 회피의 파라메트릭 방정식은

${\displaystyle X(\varphi )=4a\sin ^{2}{\tfrac {\varphi }{2}}\cos \varphi -{\tfrac {8}{3}}a\sin {\tfrac {\varphi }{2}}\cdot \sin {\tfrac {3}{2}}\varphi =\cdots ={\tfrac {4}{3}}a\cos ^{2}{\tfrac {\varphi }{2}}\cos \varphi -{\tfrac {4}{3}}a\ ,}$

${\displaystyle Y(\varphi )=4a\sin ^{2}{\tfrac {\varphi }{2}}\sin \varphi +{\tfrac {8}{3}}a\sin {\tfrac {\varphi }{2}}\cdot \cos {\tfrac {3}{2}}\varphi \ =\cdots ={\tfrac {4}{3}}a\cos ^{2}{\tfrac {\varphi }{2}}\sin \varphi \ .}$

이 방정식은 세 번째로 크고 180도 회전하며 X축을 따라 -${\displaystyle 4\frac{\mathrm{}}{}}$ 3 ${\displaystyle a}$ ${\displaystyle -{\tfrac{4}{3}a}$만큼 이동된 흉부외과를 설명한다$.$

(Trigonometric formulae were used: ${\displaystyle \sin {\tfrac {3}{2}}\varphi =\sin {\tfrac {\varphi }{2}}\cos \varphi +\cos {\tfrac {\varphi }{2}}\sin \varphi \ ,\ \cos {\tfra$$c {3}{2}}\varphi =\cdots,\\sin \varphi =2\sin {\tfrac {\barphi }{2}}\cos$ {$tfrac {\varphi },\cos \varphi =\cdots .}$)

직교 궤적

곡선의 연필 직교 궤적은 직교로 연필의 어떤 곡선과 교차하는 곡선이다. 흉부외과의 경우 다음이 해당된다.

• 방정식이 있는 흉부외과 연필의 직교 궤적

${\displaystyle r=2a(1-\cos \varphi )\,\;a>0\,\ }$

심장 박동수가 방정식을 가지고 있다.

${\displaystyle r=2b(1+\cos \varphi )\ ,\;b>0\ .}$

(두 번째 연필은 첫 번째 연필의 y축에서 반사로 간주할 수 있다. 도표를 참조하십시오.)

증명:
함수 $r{\displaystyle (}$ ${\displaystyle \phi }$) ${\displaystyle$ r$(\varphi )}$에 의해 극좌표로 주어진 곡선의 경우 데카르트 좌표에 대한 다음 연결이$$ 유지됨:

${\displaystyle x(\varphi )=r(\varphi )\cos \varphi \ ,\qquad }$ ${\displaystyle y(\varphi )=r(\varphi )\sin \varphi \qquad }$

그리고 파생상품의 경우

${\dplaystyle {dx}{d\varphi }}=r'(\varphi )\cos \varphi -r(\varphi )\sin \varphi \,\qquad }}$${\d\frac {dy}{d\varphi }}=r'(\varphi )\sin \varphi +r(\varphi )\cos \varphi \.}$

두 번째 방정식을 첫 번째 방정식으로 나누면 접선 선의 데카르트 기울기가 점$({\displaystyle r}$ (${\displaystyle \phi }$) ,${\displaystyle \phi }$) ${\displaystyle (r(\varphi )),\varphi$ $)\}:$

${\displaystyle {\frac}{dx}={\frac {r'(\varphi )\sin \varphi +r(\varphi )\cos \varphi }{r'(\varphi )\cos \varphi -r(\varphi )}}.}$

$r{\displaystyle }$= 2${\displaystyle }$a(${\displaystyle 1}$- ${\displaystyle \cos }$ cos${\displaystyle \phi }$) ${\$ 및$$ $r{\displaystyle }$= ${\displaystyle \mathrm{2b}(1}$+ ${\displaystyle \cos }$ ${\displaystyle }${ ) ${\$ 식이 각각$$ 포함된 심근경화면체:

${\displaystyle {\frac {dy_{a}}{dx}}={\frac {\cos \varphi -\cos 2\varphi }{\sin 2\varphi -\sin \varphi }}\quad }$ and ${\displaystyle \quad {\frac {dy_{b}}{dx}}=-{\frac {\cos \varphi +\co$$s 2\varphi }{\sin 2\varphi +\sin \varphi }}}$

(모든 곡선의 기울기는 $\phi {\displaystyle }$ ${\displaystyle \varphi }$에만 종속되며${\displaystyle ,}$ ${\displaystyle \mathrm{파라미터}}$ $a{\displaystyle }$, b ${\displaystyle a,b}!)$
그러므로

${\displaystyle {\frac {dy_{a}}{dx}}\cdot {\frac {dy_{b}}{dx}}=\cdots =-{\frac {\cos ^{2}\varphi -\cos ^{2}2\varphi }{\sin ^{2}2\varphi -\sin ^{2}\varphi }}=-{\frac {-1+\cos ^{2}\varphi +1-\cos ^{2}2\varphi }{\sin ^{2}2\varphi -\sin ^{2}\varphi }}=-1\ .}$

즉, 다음을 의미한다. 첫 번째 연필의 곡선은 두 번째 연필의 곡선과 직교적으로 교차한다.

서로 다른 위치에서

좌표계 내에서 심근경색체의 다른 위치를 선택하면 다른 방정식이 나타난다. 이 사진은 심근경색의 4가지 가장 흔한 위치와 극지방 방정식을 보여준다.

복합분석에서

복잡한 분석에서, $지도{\displaystyle }$z → ${\displaystyle {}^{}}$ ${\displaystyle {2\mathrm{}}^{}}${\$displaystyle z\to$ z$^{2$}} 아래의 원점을 통과하는 원의 이미지는 심근경색이다$$. 이 결과의 한 가지 적용은 만델브로트 세트의 중심 주기-1 성분의 경계가 방정식에 의해 주어진 심근경색체라는 것이다.

${\displaystyle c\,=\,{\frac {1-\left(e^{it}-1\오른쪽)^{2}}{4}}\,}$

만델브로트 세트는 그 자체로 무한히 왜곡된 복제품을 포함하고 있으며 이 작은 복제품들 중 어떤 것의 중심 전구는 대략적인 심근경색이다.

카우스틱스

어떤 가성비는 심근 강화제의 형태를 취할 수 있다. 둘레의 한 점에 관한 원의 강직성은 심근경색이다. 또한, 생성 라인에 평행한 광선에 관한 원뿔의 catacostic은 단면이 심근경색인 표면이다. 이것은 오른쪽 사진에서와 같이 원뿔의 각도와 같은 각도로 멀리서 빛이 비칠 때 부분적으로 액체가 채워진 원뿔 컵에서 볼 수 있다.^[5] 원통형 컵 바닥에 있는 곡선의 모양은 네프로이드의 절반으로, 상당히 비슷하게 보인다.

참고 항목

• 리마손
• 네포이드
• 델토이드
• 비트겐슈타인의 지팡이
• 심근 마이크로폰
• 베르누이 렘니스카테
• 루프 안테나
• 무선 방향탐지기
• 무선 방향 찾기
• 야기 안테나
• 조반니 살베미니

메모들

참조

• R.C. Yates (1952). "Cardioid". A Handbook on Curves and Their Properties. Ann Arbor, MI: J. W. Edwards. pp. 4 ff.
• Wells D (1991). The Penguin Dictionary of Curious and Interesting Geometry. New York: Penguin Books. pp. 24–25. ISBN 0-14-011813-6.

외부 링크

위키미디어 커먼즈에는 Cardioids와 관련된 미디어가 있다.

• "Cardioid", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• O'Connor, John J.; Robertson, Edmund F., "Cardioid", MacTutor History of Mathematics archive, University of St Andrews
• 하티 밍싱, 코딱지만하게
• Weisstein, Eric W. "Cardioid". MathWorld.
• Weisstein, Eric W. "Epicycloid--1-Cusped". MathWorld.
• Weisstein, Eric W. "Heart Curve". MathWorld.
• 자 리, Cardioid (1998년) (이 사이트는 많은 대체 건축물을 제공한다.
• 얀 바세나르, Cardioid, (2005)