후이겐스-프레스넬 원리
Huygens–Fresnel principle
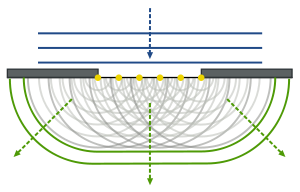
Huygens-Freshnel 원리(네덜란드 물리학자 Christiaan Huygens와 프랑스 물리학자 Augustin-Jean Freshnel의 이름을 따서 명명)는 원거리 한계와 근거리 회절 및 반사에서의 파장 전파 문제에 적용되는 분석 방법이다.그것은 파전선의 모든 점 자체가 구형 파장의 근원이며, 서로 다른 지점에서 발산되는 2차 파장은 상호 간섭한다고 기술하고 있다.[1]이 구형 파장의 합은 파도를 형성한다.
역사

1678년, Huygens는[2] 발광 장애가 도달하는 모든 지점이 구형 파동의 근원이 될 것을 제안했다; 이러한 이차 파동의 합은 이후 어느 때라도 파동의 형태를 결정한다.그는 2차파가 "앞으로" 방향으로만 이동했다고 가정했고, 왜 이런지에 대해서는 이론상 설명되지 않는다.그는 선형 및 구형파 전파에 대한 정성적 설명을 제공할 수 있었고, 이 원리를 이용하여 반사 및 굴절의 법칙을 도출할 수 있었지만, 일반적으로 회절 효과로 알려진 가장자리, 조리개 및 스크린에 빛이 부딪힐 때 발생하는 직선 전파의 편차를 설명할 수 없었다.[3]이 오류의 해결은 1991년 데이비드 A. B. 밀러에 의해 마침내 설명되었다.[4]분해능은 소스가 쌍극(Huygens가 가정하는 단극이 아님)이며, 반사된 방향으로 상쇄된다.
1818년 프레스넬은[5] Huygens의 원리와 함께 자신의 간섭 원리와 함께 빛의 직선적 전파와 회절 효과를 모두 설명할 수 있다는 것을 보여주었다.실험 결과와의 합의를 얻기 위해서는 2차 파장의 위상 및 진폭에 대한 추가적인 임의적 가정과 부차적 인자를 포함시켜야 했다.이러한 가정은 명백한 물리적 기초는 없지만 포아송 점을 포함한 많은 실험 관측치에 동의하는 예측을 이끌어냈다.
포아송은 프레스넬의 작품을 검토한 프랑스 아카데미의 회원이었다.[6]그는 프레넬의 이론을 이용하여 작은 원반 그림자의 중앙에 밝은 점이 나타나야 한다고 예측했고, 이를 통해 그 이론이 틀렸다는 추론했다.그러나 또 다른 위원인 아라고가 실험을 실시하여 예측이 정확함을 보여주었다. (리슬은 50년 전에 이것을 관찰했었다.)[3][dubious ]이것은 당시 지배적인 근육질 이론에 대한 빛의 파동 이론의 승리를 이끈 조사 중 하나였다.
안테나 이론과 공학에서, 전류원을 방사하기 위한 Huygens-Fresnel 원리의 개혁은 표면 동등성 원리로 알려져 있다.[7][8]
현미경 모델로서의 Huygens의 원리
Huygens-Freshnel 원리는 빛의 고전파 전파에 대한 이해와 예측을 위한 합리적인 근거를 제공한다.그러나 원칙에는 한계가 있는데, 즉 프레넬로 인한 키르호프의 회절 공식과 근거리 영역의 근사치를 도출하기 위해 행한 것과 동일한 근사치가 있다.이러한 것들은 빛의 파장이 어떤 광학 구성 요소와 마주치는 치수보다 훨씬 작다는 사실에서 요약할 수 있다.[6]
Kirchhoff의 회절 공식은 파동 방정식을 바탕으로 회절의 엄격한 수학적 기초를 제공한다.프레스넬이 Huygens-Fresnel 방정식에 도착하기 위해 만든 임의의 가정은 이 파생의 수학에서 자동적으로 나온다.[9]
원리의 작동에 대한 간단한 예는 열린 출입구가 두 개의 방을 연결하고 그 중 한 개의 외진 구석에서 소리가 나올 때 볼 수 있다.다른 방에 있는 사람은 그 소리가 문간에서 시작된 것처럼 들릴 것이다.두 번째 방에 관한 한 문간에서 진동하는 공기가 소리의 근원이다.
현대 물리학 해석
모든 전문가들이 Huygens의 원칙이 정확한 현실의 미시적 표현이라는 것에 동의하는 것은 아니다.예를 들어, 멜빈 슈워츠는 "Huygens의 원칙은 사실 옳은 답을 주지만 잘못된 이유 때문"이라고 주장했다.[1]
이는 다음과 같은 사실에 반영할 수 있다.
- 광자와 방출의 미세한 역학은 일반적으로 전자의 가속이다.[1]
- Huygens의[10] 원래 분석에는 진폭만 포함되었다.다른 속도로 전파되는 위상이나 파장은 포함하지 않으므로(연속 매체 내에서 회절로 인한) 간섭을 고려하지 않는다.
- 또한 Huygens 분석에는 벡터 전위를 암시하는 빛에 대한 양극화는 포함되지 않으며, 대신 음파를 스칼라 전위로 설명할 수 있고 둘 사이에 독특하고 자연스러운 번역이 없다.[11]
- Huygens 설명에서는 왜 우리가 전진(후진파 또는 전선의 전진포함) 대 후진적 전진파(후진포함)만을 선택하는지에 대한 설명이 없다.[11]
- 프레스넬 근사치에는 파도 전선의 서로 다른 지점에서 오는 상이 다른 구형파의 합으로 인한 비지역적 행동의 개념이 있으며, 비지역적 이론은 많은 논쟁(예: 로렌츠 공변량이 아님)과 적극적인 연구의 대상이 된다.
- 프레스넬 근사치는 양자 확률론적 방식으로 해석할 수 있지만, 이 상태 합계(즉, 파동선의 파동)가 얼마나 물리적으로 의미 있는 상태인지 또는 원자 궤도(LCAO) 방법의 선형 결합에서와 같이 일반적인 기준으로 근사치를 더 많이 나타내는 상태들의 전체 목록인지 불분명하다.
Huygens의 원리는 산란의 중심에 있는 유효 분야를 고려하고, 작은 동요를 고려하며, 같은 의미에서 양자 광학도 고전 광학과는 양립할 수 있다는 점에서, 다른 해석은 토론과 적극적인 연구의 대상이 된다.
실내만큼 큰 상상파 전방의 모든 점이 파장을 생성하는 파인만 모델도 이러한 근사치와 확률론적 맥락에서 해석해야 하며, 이 맥락에서 원격 지점은 전체 확률 진폭에 최소로 기여할 수 있다.
양자장 이론은 광자 생성을 위한 어떠한 현미경 모델도 포함하지 않으며 단일 광자의 개념도 이론적 수준에서 정밀하게 검토되고 있다.
원리의 수학적 표현
점 P에0 위치하며 주파수 f에서 진동하는 점 선원의 경우를 고려한다.교란은 복합 진폭으로 알려진 복합 변수 U로0 설명할 수 있다.파장 λ, wavenumber k = 2π/λ의 구면파를 생성한다.비례성의 상수 내에서, P로부터0 r 거리0 거리에 위치한 Q 지점에서 1차 파형의 복잡한 진폭은 다음과 같다.
주행 거리 대비 크기가 반비례로 감소하고 위상이 주행 거리의 k배에 따라 변한다는 점에 유의하십시오.
Huygens의 이론과 파동의 중첩 원리를 이용하여, 반경0 r의 구에 있는 각 점의 기여도를 합산하여 더 먼 지점 P에서의 복잡한 진폭을 찾아낸다.프레넬은 실험 결과와의 합치를 얻기 위해 구체에 대한 2차 파동의 개별 기여에 상수, -i/λ, 추가 기울기 계수 K(χ)를 곱해야 한다는 것을 알아냈다.첫 번째 가정은 1차 파형에 대해 2차 파형이 위상 이탈 상태에서 1/4 사이클로 진동하며, 2차 파형의 크기가 1차 파형에 대해 1:210의 비율로 발생한다는 것을 의미한다.또한 그는 K( =)가 when = 0일 때 최대값을 가지며, χ = π/2일 때 0과 같았다고 가정했는데, 여기서 χ은 1차파 전선의 정상과 2차파 전선의 정상 사이의 각도다.2차 파장의 기여로 인한 P에서의 복잡한 진폭은 다음에 의해 주어진다.[13]
여기서 S는 구의 표면을 설명하고, s는 Q와 P 사이의 거리를 나타낸다.
프레스넬은 구역구축법을 이용해 서로 다른 구역에 대한 K의 대략적인 값을 알아내 실험 결과와 일치하는 예측을 할 수 있었다.[6]키르흐호프의 정리는 후이겐스-프레스넬 원리의 기본 사상을 포함한다.키르흐호프는 많은 경우, 그 정리가 프레스넬의 제형의 형성과 동등한 단순한 형태에 근사하게 추정될 수 있다는 것을 보여주었다.[6]
팽창하는 하나의 구형파로 구성된 조리개 조명의 경우 파형의 곡률 반경이 충분히 크면 Kirchhoff는 K(()에 대해 다음과 같은 표현을 했다.[6]
K는 Huygens-Freshnel 원리와 같이 χ = 0으로 최대값을 가지지만, K는 χ = π/2로 0이 아니라 χ = π으로 0과 같다.
K(χ)의 위 유도에서는 확산 개구부가 곡률 반경이 충분히 큰 단일 구형 파형에 의해 조명된다고 가정했다.그러나 이 원칙은 더 일반적인 조도를 유지한다.[13]임의의 조도는 점원의 집합으로 분해될 수 있으며, 파동 방정식의 선형성을 호출하여 원리를 각 점원에 개별적으로 적용할 수 있다.[13]K(χ)는 일반적으로 다음과 같이 표현할 수 있다.
이 경우 K는 위에 기술한 조건(최대값 χ = 0, 0 = χ/2)을 만족한다.
일반화 Huygens의 원리
많은 책과 참고문헌을 예로 들며,[14] 본 간행물에서 파인만이 언급한 것으로 일반화 후이겐스의 원칙을 언급하고 있다.[16]
파인만은 일반화된 원리를 다음과 같이 정의한다.
"사실 하이겐스의 원리는 광학에서는 정확하지 않다.그것은 Kirchoff의 (sic) 개조로 대체되며, 이는 진폭과 그 파생상품 모두를 인접 표면에 알도록 요구한다.이는 광학에서 파동 방정식이 당시 2차 순서가 된 데 따른 결과다.양자역학의 파동 방정식은 그 시대 첫 번째 순서인 만큼 물질파, 즉 시간을 대신하는 작용에 대해서는 후이겐스의 원리가 옳다."
이는 이러한 맥락에서 일반화된 원리가 양자역학의 선형성을 반영하고 있으며 양자역학 방정식이 제시간에 가장 먼저 순서가 된다는 사실을 명확히 한다.마지막으로 이 경우에 한해서만 중첩 원칙이 완전히 적용된다. 즉, 지점 P에서의 파동 기능은 P를 둘러싸는 경계 표면의 파동 중첩으로 확장할 수 있다.파동함수는 일반적인 양자역학적 의미에서 그린의 함수와 전파자의 형식주의가 적용되는 확률밀도로 해석할 수 있다.주목할 만한 것은 이 일반화된 원칙이 더 이상 광파에 적용되지 않고 "물질파"에 적용된다는 점이다.이제 위상 인자는 작용에 의해 주어지는 대로 명확해지고 왜 웨이블렛의 위상이 원래의 파동의 위상과 다르고 추가적인 프레스넬 파라미터에 의해 수정되는지에 대해서는 더 이상 혼동을 일으키지 않는다.
Greiner에 따르면 일반화된 원리는 > t 에 대해 다음과 같은 형태로 표현할 수 있다.
여기서 G는 파동함수 }}에 전파되는 일반적인 녹색함수 이 설명은 고전적 모델의 초기 프레스넬의 공식을 닮아 일반화한다.
Huygens 이론과 현대 광자파 함수
Huygens의 이론은 빛 간섭의 파동 성질에 대한 근본적인 설명으로 작용했고 프레스넬과 영에 의해 더욱 발전되었지만 G. I가 처음 수행한 저강도 이중 슬릿 실험과 같은 모든 관찰을 완전히 해결하지는 못했다.1909년 테일러1900년대 초중반에 이르러서야 양자 이론 논의, 특히 1927년 브뤼셀 솔베이 회의에서의 초기 논의는 루이 드 브로글리가 광자가 파동함수에 의해 유도된다는 자신의 드 브로글리 가설을 제안한 것이다.[17]파동 함수는 이중 슬릿 실험에서 관찰된 빛과 어둠의 띠에 대한 훨씬 다른 설명을 제시한다.이 개념에서, 광자는 많은 가능한 경로 중 하나를 무작위로 선택하는 경로를 따른다.이러한 가능한 길은 패턴을 형성한다: 어두운 곳에서는 광자가 착륙하지 않고 밝은 곳에서는 많은 광자가 착륙한다.가능한 광자 경로 세트는 광자의 원점(원자), 슬릿, 화면 등 주변 환경에 의해 결정된다.파동함수는 이 기하학에 대한 해결책이다.파동함수 접근은 1970년대와 1980년대에 이탈리아와 일본에서 전자와 함께 추가적인 이중 슬릿 실험으로 더욱 뒷받침되었다.[18]
후이겐스의 원리와 양자장 이론
Huygens의 원리는 공간의 동질성의 결과라고 볼 수 있다. 공간은 모든 위치에서 균일하다.[19]균질 공간의 충분히 작은 영역(또는 균질 매체)에서 발생하는 모든 교란은 모든 지오데틱 방향으로 해당 영역에서 전파된다.이 소동에 의해 발생하는 파도는 차례로 다른 지역에 소란을 일으키게 된다.모든 파장의 중첩은 관찰된 파장 전파 패턴을 초래한다.
공간의 동질성은 어떤 물체의 파동함수가 모든 이용 가능한 방해받지 않는 경로를 따라 전파되는 양자장 이론(QFT)의 기본이다.작용에 비례하는 위상 계수를 사용하여 가능한 모든 경로를 따라 통합하는 경우, 파장 기능의 간섭이 관측 가능한 현상을 정확하게 예측한다.파전선의 모든 지점은 파도와 같은 속도로 라이트 콘에 펼쳐지는 2차 파동의 원천으로 작용한다.새로운 파동은 2차 파동에 접하는 표면을 구성함으로써 발견된다.
기타 공간 차원
1900년 자크 하다마드는 공간적 차원의 수가 짝수일 때 후이겐스의 원리가 깨지는 것을 관찰했다.[20][21][22]이로부터, 그는 연구의 적극적인 화제로 남아 있는 일련의 추측들을 전개했다.[23][24]특히, Huygens의 원리는 Coxeter 그룹으로부터 파생된 많은 종류의 균질한 공간(그래서 예를 들어, 단순한 리알헤브라의 Weyl 그룹)을 고수하고 있는 것으로 밝혀졌다.[19][25]
달렘베르트인에 대한 Huygens의 원리에 대한 전통적인 진술은 KdV 계층을 낳고, Dirac 운영자는 AKNS 계층을 발생시킨다.[26][27]
참고 항목
| 위키미디어 커먼즈에는 휴겐스의 원칙과 관련된 미디어가 있다. |
참조
- ^ a b c "Huygens' Principle". MathPages. Retrieved 2017-10-03.
- ^ Chr. Huygens, Datectureé mu mrle (1678년 초안; Van der Aa, 1690년)이 실바누스 P에 의해 번역된 Leyden에서 출판되었다. 톰슨 어스 라이트(런던: Macmillan, 1912; Project Gutenberg 에디션, 2005), 페이지 19.
- ^ a b Heavens, O. S.; Ditchburn, R. W. (1987). Insight into Optics. Chichester: Wiley & Sons. ISBN 0-471-92769-4.
- ^ Miller, David A. B. (1991). "Huygens's wave propagation principle corrected". Optics Letters. 16 (18): 1370–1372. Bibcode:1991OptL...16.1370M. doi:10.1364/OL.16.001370. PMID 19776972. S2CID 16872264.
- ^ A. 프레넬, 오에브레스 컴플렉스 (Paris: "Mémoire sur la diffraction de la lumier)" (1818, "왕관" 1819),Imprimerie impériale, 1866–70), vol.1, pp. 247–363; partly translated as "Fresnel's prize memoir on the diffraction of light", in H. Crew (ed.), The Wave Theory of Light: Memoirs by Huygens, Young and Fresnel, American Book Co., 1900, pp. 81–144. (Not to be confused with the earlier work of the same title in Annales de Chimie et de Physique, 1:238–81, 1816.)
- ^ a b c d e Born, Max; Wolf, Emil (1999). Principles of Optics. Cambridge University Press. ISBN 978-0-521-64222-4.
- ^ Balanis, Constantine A. (2012). Advanced Engineering Electromagnetics. John Wiley & Sons. pp. 328–331. ISBN 978-0-470-58948-9.
- ^ Balanis, Constantine A. (2005). Antenna Theory: Analysis and Design (3rd ed.). John Wiley and Sons. p. 333. ISBN 047166782X.
- ^ Klein, M. V.; Furtak, T. E. (1986). Optics (2nd ed.). New York: John Wiley & Sons. ISBN 0-471-84311-3.
- ^ "Huygens". Archive.org. Retrieved 2020-07-02.
- ^ a b "TheoryOfHuygens". Archive.org. 1939.
- ^ "Los Alamos Science". 2002.
- ^ a b c J. Goodman (2005). Introduction to Fourier Optics (3rd ed.). Roberts & Co Publishers. ISBN 978-0-9747077-2-3.
- ^ a b Greiner W. Quantum Electrodynamics. Springer, 2002.
- ^ Enders, Peter (2009). "Huygens' Principle as Universal Model of Propagation" (PDF). Latin-American Journal of Physics Education. 3 (1): 19–32.
- ^ Feynman, R. P. (1 April 1948). "Space-Time Approach to Non-Relativistic Quantum Mechanics". Reviews of Modern Physics. 20 (2): 367–387. Bibcode:1948RvMP...20..367F. doi:10.1103/RevModPhys.20.367.
- ^ Baggott, Jim (2011). The Quantum Story. Oxford Press. p. 116. ISBN 978-0-19-965597-7.
- ^ Peter, Rodgers (September 2002). "The double-slit experiment". www.physicsworld.com. Physics World. Retrieved 10 Sep 2018.
- ^ a b Veselov, Alexander P. (1995). "Huygens' principle and integrable systems". Physica D: Nonlinear Phenomena. 87 (1–4): 9–13. Bibcode:1995PhyD...87....9V. doi:10.1016/0167-2789(95)00166-2.
- ^ Veselov, Alexander P. (2002). "Huygens' Principle" (PDF). Archived from the original (PDF) on 2016-02-21.
- ^ "Wave Equation in Higher Dimensions" (PDF). Math 220a class notes. Stanford University.
- ^ Belger, M.; Schimming, R.; Wünsch, V. (1997). "A Survey on Huygens' Principle". Zeitschrift für Analysis und ihre Anwendungen. 16 (1): 9–36. doi:10.4171/ZAA/747.
- ^ Ásgeirsson, Leifur (1956). "Some hints on Huygens' principle and Hadamard's conjecture". Communications on Pure and Applied Mathematics. 9 (3): 307–326. doi:10.1002/cpa.3160090304.
- ^ Günther, Paul (1991). "Huygens' principle and Hadamard's conjecture". The Mathematical Intelligencer. 13 (2): 56–63. doi:10.1007/BF03024088. S2CID 120446795.
- ^ Berest, Yu. Yu.; Veselov, A. P. (1994). "Hadamard's problem and Coxeter groups: New examples of Huygens' equations". Functional Analysis and Its Applications. 28 (1): 3–12. doi:10.1007/BF01079005. S2CID 121842251.
- ^ Chalub, Fabio A. C. C.; Zubelli, Jorge P. (2006). "Huygens' Principle for Hyperbolic Operators and Integrable Hierarchies". Physica D: Nonlinear Phenomena. 213 (2): 231–245. Bibcode:2006PhyD..213..231C. doi:10.1016/j.physd.2005.11.008.
- ^ Berest, Yuri Yu.; Loutsenko, Igor M. (1997). "Huygens' Principle in Minkowski Spaces and Soliton Solutions of the Korteweg-de Vries Equation". Communications in Mathematical Physics. 190 (1): 113–132. arXiv:solv-int/9704012. Bibcode:1997CMaPh.190..113B. doi:10.1007/s002200050235. S2CID 14271642.
추가 읽기
- 스트랫튼, 줄리어스 아담스:전자기 이론, 맥그라우 힐, 1941. (Wiley – IEEE Press, ISBN 978-0-470-13153-4)
- B.B. 베이커와 E.T.콥슨, Huygens의 원리 수학 이론, 옥스포드, 1939, 1950; AMS Chelsea, 1987.