기하학 광학

기하학 광학 또는 광선 광학은 광선의 관점에서 빛의 전파를 설명하는 광학의 모델입니다.기하학 광학에서 광선은 특정 상황에서 빛이 전파되는 경로를 근사하는 데 유용한 추상화입니다.

기하학적 광학의 간단한 가정에는 다음과 같은 광선이 포함됩니다.

• 균질한 배지로 이동할 때 직선 경로로 전파되는
• 구부러짐, 특정 상황에서는 2개의 다른 매체 사이의 인터페이스로 분할될 수 있습니다.
• 굴절률이 변화하는 매체에서 곡선을 따라가는
• 흡수되거나 반사될 수 있다.

기하학적 광학은 회절이나 간섭과 같은 특정 광학 효과를 설명하지 않습니다.이 단순화는 실제로 도움이 됩니다.빛이 상호작용하는 구조의 크기에 비해 파장이 작을 때 훌륭한 근사치입니다.이 기법은 광학 수차를 포함한 이미징의 기하학적 측면을 설명하는 데 특히 유용합니다.

설명.

광선은 빛의 파장에 수직인 선이나 곡선을 말합니다(따라서 파장 벡터와 일직선이 됩니다).광선에 대한 조금 더 엄격한 정의는 광선에 의해 두 지점 사이에 있는 경로가 가장 짧은 ^[1]시간에 횡단할 수 있는 경로라는 페르마의 원리에서 따랐습니다.

기하학적 광학은 종종 근축 근사 또는 "작은 각도 근사"를 만들어 단순화됩니다.그러면 수학적 동작이 선형화 되어 광학 부품과 시스템이 단순한 행렬로 설명될 수 있게 됩니다.이는 가우스 광학 및 근축 광선 추적 기술로 이어지며, 대략적인 이미지 및 객체 위치 및 ^[2]확대와 같은 광학 시스템의 기본 특성을 찾는 데 사용됩니다.

반사

거울과 같은 광택 있는 표면은 간단하고 예측 가능한 방법으로 빛을 반사합니다.이를 통해 공간 내 실제(실제) 위치 또는 추정(가상) 위치와 연관지을 수 있는 반사 이미지를 생성할 수 있습니다.

이러한 표면에서 반사광의 방향은 입사광이 표면 법선과 이루는 각도, 즉 광선이 부딪치는 지점에서 표면에 수직인 선에 의해 결정된다.입사광과 반사광은 단일 평면에 존재하며 반사광과 표면 법선 사이의 각도는 입사광과 ^[3]법선 사이의 각도와 같다.이것은 반성의 법칙으로 알려져 있다.

평면 거울의 경우, 반사의 법칙은 물체의 이미지가 직립하고 거울 앞에 있는 물체와 거울 뒤의 거리가 같다는 것을 의미합니다.이미지 크기는 개체 크기와 동일합니다.(평면 거울의 배율은 1입니다.)또한 이 법칙은 미러 이미지가 패리티 반전임을 의미하며, 이는 좌우 반전이라고 인식됩니다.

곡면이 있는 거울은 표면의 각 지점에서 반사 법칙을 사용하여 광선을 추적하여 모델링할 수 있습니다.포물선 표면이 있는 거울의 경우 거울에 입사한 평행 광선이 공통 초점에 수렴하는 반사 광선을 생성한다.다른 곡면도 빛의 초점을 맞출 수 있지만, 분산된 형상으로 인해 초점이 우주에서 흐려지게 됩니다.특히 구면 거울은 구면 수차를 보인다.곡선 미러는 1배 이상 또는 그 이하의 배율로 이미지를 형성할 수 있으며, 이미지는 수직 또는 반전될 수 있습니다.거울에 반사되어 형성된 직립상은 항상 가상이지만 반전상은 실재하여 스크린에 ^[3]투영할 수 있다.

굴절

이 섹션에는 다른 기사의 요약 또는 요약이 포함되어 있어야 합니다.Wikipedia 참조:이 문서의 주요 텍스트 또는 다른 문서의 주요 텍스트에 통합하는 방법에 대한 요약 스타일입니다. (2009년 6월)

굴절은 빛이 굴절률이 변화하는 공간의 영역을 통과할 때 발생합니다.가장 간단한 굴절 사례는 $굴절률$이$1인$$$균일한 $매체$와 $굴절률$이$2인$ 다른 매질 사이에 계면이 있을 때 발생합니다$.$ 이러한 상황에서 스넬의 법칙은 광선의 굴절 결과를 다음과 같이 설명합니다.

${\displaystyle n_{1}\sin \theta _{1}=n_{2}\sin \theta _{2}\}$

여기서 ${\displaystyle {1\mathrm{}}_{}}$ 1$$\ $displaystyle \theta _$ {$$} ${\$ 2 \ displaystyle \$theta _$ {2} where 、 ${\displaystyle {2\mathrm{}}_{}}$ where where 、 2 2 \ $displaystyle \theta$ _ {$$}는$$$$ 각각 (인터페이스에 대한) 정상과 입사 및 굴절파 사이의 각도입니다.이 현상은 위에서 설명한 굴절률의 정의에서 볼 수 있듯이 빛의 속도 변화와도 관련이 있으며, 이는 다음을 의미한다.

${\displaystyle v_{1}\sin \theta _{2}\=v_{2}\sin \theta _{1}$

$여기$서 $({$}}) $및$ $({$는 각 미디어를 통과하는 ^[3]파속입니다.

스넬의 법칙의 다양한 결과로는 굴절률이 높은 물질에서 굴절률이 낮은 물질로 이동하는 광선의 경우 계면과의 상호작용이 제로 투과가 될 수 있다는 사실을 들 수 있다.이 현상을 토탈 내부 반사라고 하며, 광섬유 기술을 가능하게 합니다.광신호가 광섬유케이블을 통과하면 광신호는 내부 반사를 통해 케이블 길이 전체에 걸쳐 빛을 잃지 않습니다.반사 및 굴절의 조합을 사용하여 편광선을 발생시킬 수도 있습니다.굴절광선과 반사광이 직각을 이루면 반사광선은 "평면 편광"의 특성을 갖는다.이러한 시나리오에 필요한 입사각을 브루스터 [3]각도라고 한다.

스넬의 법칙은 굴절률과 매체의 기하학적 구조를 알면 광선이 "선형 매체"를 통과할 때 편향을 예측하는 데 사용할 수 있다.예를 들어 프리즘을 통한 빛의 전파는 프리즘의 모양과 방향에 따라 빛이 편향되는 결과를 낳는다.또한 빛의 주파수가 다르면 대부분의 물질에서 굴절률이 약간 다르기 때문에 굴절을 사용하여 무지개로 보이는 분산 스펙트럼을 생성할 수 있다.프리즘을 통해 빛을 통과할 때 이 현상을 발견한 것은 아이작 ^[3]뉴턴에 의한 것으로 유명하다.

일부 매체는 위치에 따라 서서히 변화하는 굴절률을 가지며, 따라서 광선이 직선이 아닌 매체를 통해 휘어집니다.이 효과는 공기 굴절률의 변화로 인해 빛이 굴절되어 멀리(물웅덩이의 표면과 같은)에서 반사되는 것처럼 보이는 더운 날에 나타나는 신기루의 원인이 됩니다.굴절률이 다양한 재료를 그라데이션 인덱스(GRIN) 재료라고 하며 복사기와 스캐너를 포함한 현대 광학 스캔 기술에 사용되는 많은 유용한 특성을 가지고 있습니다.이 현상은 구배지수 ^[4]광학 분야에서 연구된다.

굴절에 의해 집광 또는 발산되는 광선을 생성하는 장치를 렌즈라고 한다.얇은 렌즈는 렌즈 제조사의 ^[5]방정식을 사용하여 모델링할 수 있는 양쪽에 초점을 만듭니다.일반적으로 평행광선을 수렴시키는 볼록렌즈와 평행광선을 발산시키는 오목렌즈의 두 종류가 있다.이 렌즈에 의해 어떻게 이미지가 생성되는지에 대한 자세한 예측은 곡선 거울과 유사한 광선 추적을 사용하여 이루어질 수 있습니다.커브 미러와 마찬가지로, 얇은 렌즈는 특정 초점 $(f$\display $style$f)와 물체 거리(${\displaystyle {S\mathrm{}}_{}}$1\$display style S_{$1})$$에 주어진 이미지의 위치를 결정하는 간단한 방정식을 따릅니다.

${\displaystyle {1} {S_{1}} + {\frac {1} {S_{2}} = flac {1} {f}}$

$여기$서 S $(\$는 이미지와 관련된 거리이며, 관례상 물체와 같은 쪽에 있는 경우 음,^[5] 반대쪽에 있는 경우 양으로 간주됩니다.초점거리 f는 오목렌즈의 경우 음으로 간주됩니다.

입사하는 평행광선은 볼록렌즈에 의해 렌즈로부터 1초점 거리, 렌즈의 반대쪽의 반전 실화상으로 집속된다.

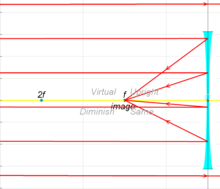
유한 거리에 있는 물체로부터의 광선은 초점 거리보다 렌즈로부터 더 멀리 집속됩니다.물체가 렌즈에 가까울수록, 화상은 렌즈로부터 멀리 떨어져 있습니다.오목렌즈에서는 입사하는 평행광선이 렌즈를 통과한 후 발산되며, 평행광선이 접근하고 있는 렌즈의 같은 쪽에서 렌즈로부터 한 초점 거리에 있는 수직 가상상에서 발생한 것처럼 보인다.

유한 거리에서의 물체로부터의 광선은 초점 거리보다 렌즈에 가깝고 물체와 같은 쪽에 있는 가상 화상과 관련지어진다.물체가 렌즈에 가까울수록 가상 이미지는 렌즈에 더 가깝습니다.

마찬가지로, 렌즈의 배율은 다음과 같이 주어진다.

${\displaystyle M=-{\frac {S_{2}}}{S_{1}}=black {f}{f-S_{1}}}$

여기서 음수 부호는 관례상 양수 값에는 직립 물체를, 음수 값에는 반전 물체를 나타낸다.거울과 마찬가지로, 단일 렌즈로 생성된 수직 이미지는 가상이고 반전 이미지는 실제입니다.^[3]

렌즈는 영상과 초점을 왜곡하는 이상 현상을 겪는다.이는 기하학적 결함 및 빛의 다양한 파장에 대한 굴절률 변화(색수차)^[3]에 기인합니다.

기초 수학

수학적인 연구로서 기하학적 광학은 쌍곡선 편미분방정식에 대한 해답의 단파장 한계(소머펠트-룽지법) 또는 맥스웰 방정식에 따른 필드 불연속성의 전파 특성(루네부르크법)으로 나타난다.이 단파장 한계에서는 다음과 같이 국소적으로 용액을 근사할 수 있다.

$(\displaystyle u(t,x)\apprough a(t,x)e^{i(k\cdot x-\obega t)})$

$여기$서 k${\displaystyle }$,$$ { $displaystyle$ k , \ $omega$}는$$ 분산 관계를 충족하며 $진폭{\displaystyle }$a (${\displaystyle t}$ ,${\displaystyle x}$ $){$ $displaystyle$a ($t$ ,$x$ )}는$$ 천천히 변화합니다.보다 정확하게 말하면, 톱 오더 솔루션은 다음과 같은 형태가 됩니다.

${\displaystyle a_{0}(t,x)e^{i\varphi(t,x)/\varepsilon}}$

${\displaystyle 위상}$ ${\displaystyle (}$ ( ${\displaystyle t}$,${\displaystyle }$x${\displaystyle }$) / $（$ \ $displaystyle$\$varphi ( t$ ,$x$ ) / \ $varepsilon }$는 선형화할 수 있으며, 큰 $wavenumber{\displaystyle }$k : ${\displaystyle =}$ ${\displaystyle {\mathrm{}}_{}}$ {\$x$$displaydisplaydisplaydisplaydisplaydisplaydisplaydisplay$ -display ${\displaystyle {}_{}}$= :$=$\ $displaystyle$$$k : \ $varph$$}$및 $large$ large large large large large large large large large large large large large $=$ - large large large large large large large large large large large large large large large large large large large large large large large large large large large large large large large 방정식작은 파라미터 $"{$은(는) 진동 초기 조건으로 인해 씬(scene)에 들어갑니다.따라서 초기 조건이 미분 방정식의 계수보다 훨씬 빠르게 진동할 경우 용액은 매우 진동하며 광선을 따라 전송됩니다.미분 방정식의 계수가 매끄럽다고 가정하면 광선도 매끄럽습니다.즉, 굴절은 일어나지 않습니다.이 기술의 동기는 짧은 파장 빛이 이동 시간을 최소화하는 광선을 따라 이동하는 전형적인 광전파 시나리오에서 비롯됩니다.풀 어플리케이션에는 마이크로 로컬 분석 툴이 필요합니다.

소머펠트-룽게법

제로 파장의 한계를 취함으로써 기하학적 광학 방정식을 얻는 방법은 1911년 ^[6]아놀드 소머펠트와 J. 룽지에 의해 처음 설명되었습니다.그들의 유래는 피터 데바이의 ^[7][8]구두 발언에 기초했다.단색 스칼라장${\displaystyle }display{\displaystyle }$ (${\displaystyle r\mathbf{}}$ ,$t$ ) $=$ (${\displaystyle }$r ) ${\displaystyle e^{}}$ ${\displaystyle {\mathrm{display}}^{}}$ t$$t \ $displaystyle$\$psi$ ( \ $mathbf { r } e^$ {$i$ \ $obega$ t$}$。여기서$display{\displaystyle }$ { $displaystyle \psi }$는 전기장 또는 자기장의 컴포넌트 중 하나일 수 $.$

$\displaystyle \displayla ^{2}\phi +k_{o}^{2}n(\mathbf {r})\phi = 0}$

${\displaystyle {여기}_{}}$서 k o ${\displaystyle {}_{}\omega }$ / ${\displaystyle c}$ ${\displaystyle =}$ ${\displaystyle 2\pi }$ / {\$$ { $displaystyle k _$ { o } = \$메가$ / c =$$2 \ pi / \ $da displayda _$ {$$o}이며$,$ $c{\displaystyle }$ { \ $displaystyle$ c$}$는 진공 상태에서의 빛의 속도입니다.$여기$서 n$)$ {$displaystyle$ n$(\mathbf {r})}$은 매체의 굴절률이다.일반성을 잃지 않고, 방정식을 다음과 같이 변환하기 위해 $\theta {\displaystyle }$ ${\displaystyle =A}$ ( ${\displaystyle k_{}}$o ,${\displaystyle r\mathbf{}}$ ) $e$ ${\displaystyle {{}_{}}^{}}$ ${\displaystyle {k_{}}^{}}$ ${\displaystyle {{}_{}}^{}}$S (${\displaystyle {r\mathbf{}}^{}}$) \ $displaystyle \phi = A$ ( $k$_ {$o$, \ $mathbf {$ $r$} ) e$^{ik$_ {$o }$ S ( \ $mathbf${ r } ) } } 를 소개합니다$$.

${\displaystyle -k_{o}^{2}A[(\nabla S)^{2}-n^{2}+2ik_{o}(\nabla S\cdot \nabla A)+ik_{o}A\nabla ^{2}S+\nabla ^{2}A=0.}$

기하학적 광학의 기본 원리는 ${\displaystyle o_{}}$~ ${\displaystyle k_{}^{}}$o - ${\displaystyle 1_{}^{}}$ ${\displaystyle {}_{}^{}}$ {\$displaystyle \displayda$ _${o}\sim$ k_${o}^{-1}\rightarrow$ 0$\}$에 있으므로 다음과 같은 점근 급수가 가정됩니다.

${\displaystyle A(k_{o},\mathbf {r})=\sum _{m=0}^{\infty}{\frac {A_{m}(\mathbf {r})}{(ik_{o}}^{m}}}}}$

For large but finite value of ${\displaystyle k_{o}}$, the series diverges, and one has to be careful in keeping only appropriate first few terms.${\displaystyle k_{}}$o(\$displaystyle k_{o$의 각 값에 대해 유지할 최적의 항 수를 찾을 수 있으며, 최적 수보다 많은 항을 더하면 ^[9]근사치가 낮아질 수 있습니다.열을 방정식에 대입하고 서로 다른 차수의 항을 수집하면 다음과 같은 결과를 얻을 수 있습니다.

$디스플레이 스타일O(k_{o}^{2}):&\sys (\sysla S)^{2}=n^{2},\O(k_{o}):&\quad 2\nabla S\cdot\nabla A_{0}+A_{0}\nabla ^{2}S=0,\O(1):&\quad 2\navla S\cdot \navla A_{1}+A_{1}\nabla ^{2}S=-\nabla ^{2}A_{0},\end{aligned}}$

일반적으로

$({displaystyle O(k_{o}^1-m):\quad 2\nabla S\cdot\nabla A_{m}+A_{m}\nabla ^{2}S=-\nabla ^{2}A_{m-1}.}$

첫 번째 방정식은 $eikonal{\displaystyle }$S${\displaystyle }$($$r ) (\$displaystyle$S (\$mathbf${r$}$ )를 결정하는 eikonal 방정식으로 알려져 있으며, 예를 들어 다음과 같이 데카르트 좌표로 작성된 해밀턴-야코비 방정식이다.

${{displaystyle\left S}{\partial x}\right}^{2}+\leftfrac{\partial y}\right}^2}+\frac{\partial z}\right}^2}=n^2}.}$

나머지 방정식은 함수 ${\displaystyle A_{}}$m ( ${\displaystyle r\mathbf{}}$ $){displaystyle A_{m}(\mathbf {r$을 결정합니다.

루네부르크법

맥스웰 방정식에 대한 해법의 불연속성 표면을 분석함으로써 기하학적 광학 방정식을 얻는 방법은 1944년 ^[10]루돌프 칼 루네부르크에 의해 처음 기술되었다.$진폭{\displaystyle }$ A(k o${\displaystyle {}_{}r\mathbf{}}$)(\$displaystyle A(k_{o$},\$mathbf${r$})$ 및$$ $위상{\displaystyle }$ S$r)$ {$displaystyle$S(\$mathbf${r})}가$$ ${\displaystyle \underset{}{{방정식\mathrm{}}_{}}}$ k${\displaystyle \mathrm{}\frac{{}_{}}{}}$ ${\displaystyle \underset{}{}\frac{\mathrm{}}{}}$ K(${\displaystyle r\frac{\mathrm{}}{}}$$)$를 만족하는 소머펠트-룬지 방법에 필요한 특수한 형태를 갖도록 제한하지 않습니다.${\displaystyle \frac{1}{}}$ 2${\displaystyle {\mathrm{}}^{}}$S) $=$ ${\displaystyle 0}$(\$displaystyle \lim$ _${k_{0}\to$ \$infty$}{1$\over$ k_${0}}\$lefth$1 \over$ A$},\nabla$ S$\cdot \cdot$ \cdot A$+{1 \over$ 2)\$la ^{$2}\$la$ ^{$2}S\$right)=$0$ 단, 이 조건은 파형에 의해 충족됩니다.

Luneburg 접근법의 주요 결론은 다음과 같다.

정리.$필드{\displaystyle \stackrel{}{\mathbf{}}}$ E ${\displaystyle \to }$ ( ${\displaystyle x}$,${\displaystyle y}$ ,${\displaystyle z}$ , t$){$ $displaystyle \mathbf {E}$ ($x$$$, ${\displaystyle y}$$$, z , ${\displaystyle t}$ $)$및 H ${\displaystyle \to }$ ( x${\displaystyle }$, y ,${\displaystyle z}$, t $){$ $displaystyle \mathbf {H}$ ($x , y$${\displaystyle }$,$z$ ,$t$ ) (${\displaystyle x}$ ${\displaystyle ,}$ z , t ) $$${\displaystyle ）}$ 。$\mu(x,y,z$는 $R{\displaystyle }$ $($,${\displaystyle y,z)}$ - ${\displaystyle c}$ t $=$ ${\displaystyle 0}($$x,y,z)$로 나타나는 (이동$)$ 표면을 따라 유한한 불연속성을 가진다.적분 형태의 맥스웰 방정식은 $\displaystyle\psi}$이(가) 아이코날 방정식을 만족한다는 것을 의미합니다.

${\displaystyle {\mathrm{}}_{}^{}}$ x${\displaystyle {}_{}^{}{}_{}^{}}$ + ${\displaystyle {}_{}^{}}$y ${\displaystyle {}_{}^{}}$ + ${\displaystyle \psi }$ z 2${\displaystyle {}_{}^{}}$= $μ μ$=$$ 2 { \$displaystyle$\psi $_ {$x$}^{$2} + \$psi _$ ${z }^{2$} + \$varepsilon$ \mu$= n$$2$} 、

$여기$서$$n {\$displaystyle$ n$}$은 매체(가우스 단위)의 굴절률입니다.

이러한 불연속면의 예로는 특정 순간에 방사를 시작하는 소스에서 방출되는 초기파전면이 있다.

따라서 필드 불연속 표면은 다음과 같이 정의된 해당 지오메트리 광학장과 함께 지오메트리 광학파 전선이 됩니다.

$\mathbf {E} ^{*}(x,y,z)=\mathbf {E}(x,y,z,\psi(x,y,z)/c}$

${\displaystyle \mathbf {H} ^{*}(x,y,z)=\mathbf {H}}(x,y,z,\psi(x,y,z)/c)}$

이러한 필드는 소머펠트-룽게 접근법의 전송 방정식과 일치하는 전송 방정식을 따릅니다.루네부르크 이론에서 광선은 불연속 표면에 직교하는 궤적으로 정의되며 올바른 매개 변수화를 통해 페르마의 최소 시간 원리를 따르는 것으로 보여 표준 광학의 광선으로 광선의 동일성을 확립할 수 있습니다.

위의 개발은 이방성 ^[11]매체로 일반화할 수 있다.

뤼네부르크 정리의 증명은 맥스웰 방정식이 해법의 불연속성 전파를 어떻게 지배하는지 조사하는 것에 기초한다.기본적인 기술 조항은 다음과 같습니다.

기술적인 보조군.$\delta {\displaystyle }$(${\displaystyle x}$ ,${\displaystyle y}$ ,${\displaystyle z}$ ,${\displaystyle t}$ ) ${\displaystyle \stackrel{}{\mathbf{=}}}$$$ { \ $displaystyle$ \ $varphi ( x$ , y , z , t )= $0$${\displaystyle \}}$을 $시공간{\displaystyle {\mathbf{}}^{}}$ R $(\$displaystyle $\mathbf$ {R$}$$^{$4$})$의 $하이퍼서페이스$(\$displaystyle$ {${\displaystyle x}$ ${\displaystyle ,y}$ ,${\displaystyle z}$ ,$})$라고 합니다.$c {H}}$ ($x,y,z,t$ ,${\displaystyle }$(${\displaystyle x,y,z}$), {$displaystyle \varepsilon (x,y,z$${\displaystyle }\mu {\displaystyle }$ ($)$ {$displaystyle \mu (x,y,z$는 유한 불연속성을 가집니다.그런 다음 하이퍼서페이스의 각 지점에서 다음 공식이 적용됩니다.

${\displaystyle \varphi \times [\mathbf {H}}-{1 \over c},\varphi _{t},[\varepsilon \mathbf {E}}=0}$

$\displaystyle \varphi \times [\mathbf {vec {E}} + {1 \over c},\varphi _{t},[\mu \mathbf {H}}=0}$

$\displaystyle \cdot [\varepsilon \mathbf \vec {E}} = 0 }$

$\displaystyle \cdot [\mu \mathbf {H}} = 0 }$

$여기$서$displaystyle$ \$displayla$$}$ 연산자는 ${\displaystyle \mathrm{xyz}}$(${\displaystyle \mathrm{고정}}$ t$$\$displaystyle$$xyz$$)$ $-공간$에 작용하며, 각 괄호는 불연속 표면의 양쪽 값 차이(예: 임의의 규칙이지만 고정된 규칙(예: 경사 θ$\displaystyle\)$를 나타냅니다.$nabla \varphi }$가 감산되는 수량의 방향을 가리킵니다).

증거 스케치소스(가우스 단위)에서 떨어진 Maxwell의 방정식부터 시작합니다.

$\displaystyle \cdot \varepsilon \mathbf {E} = 0$

$\displaystyle \cdot \mu \mathbf {H}} = 0$

$\displaystyle \times \mathbf {E} +{\mu \over c},\mathbf {H}_{t}=0}$

$\displaystyle \times \mathbf {H} - {\varepsilon \over c}, \mathbf {E} _{t}=0}$

${\displaystyle {\mathrm{}}^{}}$$$$4$의 Stokes 정리(\${\displaystyle {\mathrm{}}^{}}$ $\mathbf {R}$^{$4})$를 사용하면$$ R$$4의 도메인$$ D$(\$$displaystyle$$$$\mathbf {R} ^{4$})에 대해 부분적인 평활 경계$\delta {\displaystyle \mathrm{}}$(\$displaystyle$ \$gamma }$ ） 。

$\displaystyle \point _{\Gamma}(\mathbf {M}}\cdot \varepsilon \mathbf {E}), dS=0}$

$여기$서 M ${\displaystyle \to }$ ( ${\displaystyle x_{}}$N , ${\displaystyle y_{}}$N , ${\displaystyle {}_{}{N}_{}}$ )$${$displaystyle \mathbf {M}$=$(x_{N},y_{N$},$z_{N})$는 외향 단위${\displaystyle {}_{}}$(${\displaystyle x_{}}$N,${\displaystyle y_{}}$ ${\displaystyle {}_{}{}_{}{z}_{}}$N,${\displaystyle t_{}}$ N$)$의 투영입니다. {style$(x_{N},z_{N})$$m {const$ 및 $d{\displaystyle }$ $({displaystyle$$dS$는$δ$의 볼륨3 폼입니다.마찬가지로 나머지 Maxwell의 방정식으로부터 다음 값을 구합니다.

$\displaystyle \point _{\Gamma}(\mathbf {M}}\cdot \mu \mathbf {H}}), dS=0}$

$\displaystyle \point _{\Gamma}(\mathbf {Vec {M}) \times \mathbf {E} +{\mu \over c},t_{N},\mathbf {Vec {H}}),d=0}$

$\displaystyle \point _{\Gamma}(\mathbf {M})\times \mathbf {vec {H}}-{\varepsilon \over c},t_{N},\mathbf {E}),S=0}$

여기서 $임의$의 작은 서브 인터페이스$$$({$$displaystyle\Gamma})$을 고려하여 ${\displaystyle {}^{}}$에서$$$(\$$displaystyle\gamma_{0$을 둘러싼 작은 네이버를 설정하고 위의 적분을 뺍니다.

$\displaystyle \int _{\Gamma _{0}(\varphi \cdot [\varepsilon \mathbf \vec {E}}), {dS \over \\displaystyle ^{4D}\varphi \} =0})$

$\displaystyle \int _{\Gamma _{0}}(\displayla \varphi \cdot [\mu \mathbf {vec {H}}), {dS \over \displayla ^{4D}\varphi \} =0})$

$\displaystyle \int _{0}}\left(\la \varphi \times [\mathbf \vec {H}})-{1 \over c},\varphi _{t},[\varepsilon \mathbf {E}\right], {D}, {DS \over \gampi}, \varf {\la ^4},\vari},\phi},\la },\phi}, {\phi}, {\ph},$

$\displaystyle \int _{0}}\left(\displayla \varphi \times [\mathbf {vec {E}})+{1 \over c},\varphi _{t},[\mu \mathbf {H},\right], {ds\gambf {0} \dvarpi} =\dvari } =PH}$

${\displaystyle {여기}^{}}$서 $\S {\displaystyle {\mathrm{}}^{}}$ $(\displaystyle$ \$nabla$^{$4D})$는 $4D{\displaystyle }$ x ${\displaystyle y}$ ${\displaystyle z}$ t$(\displaystyle xyzt)$ 공간의$$ 구배를 나타냅니다.$또한{\displaystyle {\mathrm{}}_{}}$ ${\displaystyle {\delta \mathrm{}}_{}}$0$(\displaystyle$ \$Gamma _{$0$$})은 임의이므로 인테그란드는 0이어야 하며 이는 보조항목을 증명합니다.

이제 그것들이 연속적인 매질을 통해 전파될 때 불연속 표면이 아이코날 방정식을 따른다는 것을 쉽게 알 수 있습니다.구체적으로$\epsilon {\displaystyle }$ { $displaystyle$\$varepsilon$${\displaystyle \}}$ $및$ μ { $displaystyle \ mathbf { E}}$ 및$$ $H$${\displaystyle \stackrel{}{\mathbf{\to }}}$ \ $displaystyle$\$mathbf${ $H}$ ${\displaystyle \stackrel{}{\mathbf{=}}}$ [$$]의 ${\displaystyle 불연속성}$은 다음과 같습니다$.{\displaystyle }$$엡실론 [\mathbf {E}}$${\displaystyle }$및$$ [${\displaystyle \mu \stackrel{}{\mathbf{}}}$ H ${\displaystyle \to }$ ]${\displaystyle \mu }$ [ ${\displaystyle H\stackrel{}{\mathbf{}}}$ ${\displaystyle \to }$ $]$ { $displaystyle$[\$mu \mathbf {H}} =$ \$mu$[\$mathbf {H}}}$ $\}.$ 이 경우, lema의 처음 두 공식은 다음과 같이 쓸 수 있습니다.

$\displaystyle \varphi \times [\mathbf {vec {H}}-{\varepsilon \over c},\varphi _{t},[\mathbf \vec {E}}=0}$

$\displaystyle \varphi \times [\mathbf \vec {E}} + {\mu \over c},\varphi _{t},[\mathbf \vec {H}}=0}$

${\displaystyle 첫}$ 번째 방정식의 교차곱을$∇({displaystyle\nabla\varphi})$로 취하여 두 번째 수율을 대입하면 다음과 같다.

$(\displaystyle \varphi \times [\mathbf \vec {H}})-{varepsilon \over c},\varphi _{t},(\displayla \varphi {E})=(\displaystyle \var\varphi {\cdcdf})$

맥스웰 방정식의 두 번째에 따르면$,{\displaystyle \mathrm{}}$ ${\displaystyle 표면}$에 있는 $점{\displaystyle }$ $=$ ${\displaystyle 0}$$(\displaystyle \displaystyle$ \$varphi$\cdot [\$mathbf \vec${H$}})= 0$$displaystyle \varphi =0})$에 한한다.

$\displaystyle \\varphi \^{2}=varepilon \mu \over c^{2}}\varphi _{t}^{2}$

(이 단계에서 불연속성이 있으면 0으로 나누기 때문에 주의해 주십시오).

물리적인 고려를 통해 ${\displaystyle \{\backslash }$ { $displaystyle$\$varphi }$은 (${\displaystyle x}$ ,${\displaystyle y}$ ,${\displaystyle }$z ) $=$ (${\displaystyle x}$ , ${\displaystyle y}$,${\displaystyle z}$) - ${\displaystyle c}$ \$display$style \ $varphi ( x$ ,$y$ ,$z$ $)=$ \$psi ( x$ , $y$, t )-$$id의 형태로 되어 있다고 생각할 수 있습니다.$$(암묵함수 정리에 의해 ${\displaystyle {\theta }_{}}$ t${\displaystyle {}_{}0}$0 { $displaystyle$\$varphi$_ { $t$} \ $neq$0인$$ 경우 수학적으로$\theta {\displaystyle }$ { $displaystyle$\$psi$}가$$ 존재합니다.)$§(\displaystyle\psi)$로 작성된 위의 방정식은 다음과 같습니다.

$(\displaystyle \\displayla \psi \^{2}=displayvarepsilon \mu \over c^{2}},(-c)^{2}=\varepsilon \mu =n^{2}})$

예.,

${\displaystyle \psi _{x}^2}+\psi _{y}^2}+\psi _{z}^2}=n^{2}}$

변수$t{\displaystyle }$ {\$displaystyle$ t$$$}$가 없기 때문에 모든$x{\displaystyle }$ {\$displaystyle$$},$ y {\$displaystyle$$},$ z {\$displaystyle$ z$\}$에 대한 eikonal 방정식입니다.스넬의 법칙이나 프레넬 공식과 같은 다른 광학 법칙도 $마찬가지$로 $§(\displaystyle\varepsilon)$ $및$ μ(\$displaystyle\mu$의 불연속성을 고려함으로써 얻을 수 있습니다.

4벡터 표기법을 사용한 일반 방정식

특수 상대성 이론에서 사용되는 4벡터 표기법에서, 파동 방정식은 다음과 같이 쓸 수 있다.

${\displaystyle\frac {\psi}{\display x_{i}\display x^{i}=0}$

$치환{\displaystyle }$ ${\displaystyle =}$ ${\displaystyle {Ae}^{}}$ i ${\displaystyle S^{}}$/ {\$$（ \ $displaystyle \psi$=$Ae^{iS/\epsilon$}} ）는$$ 다음과^[12] 같습니다.

${\displaystyle - {\frac {A} {\epsilon ^{2}} {\frac {partial S} {\partial x_i} {\frac {2i} {\epsilon } {\frac {partial A} {\i} {\frac {\frac {partial S}A}{\partial x_{i}\partial x^{i}}=0.}$

따라서 eikonal 방정식은 다음과 같이 주어진다.

${\displaystyle {\frac S} {\frac S} {\frac S} {\partial x^{i}} = 0.}$

일단 위의 방정식을 풀어서 아이코날(eikonal)을 찾으면, 파동 4벡터는 다음에서 찾을 수 있다.

${\displaystyle k_{i}=-{\frac S}{\partial x^{i}}}.}$

「 」를 참조해 주세요.

• 해밀턴 광학
• 기하학적 음향학

참조

추가 정보

• Robert Alfred Herman(1989) 기하학적 광학에 관한 논문(Archive.org).
• "눈의 빛과 시각의 계몽된 풍경"은 아랍어로 기하학적 광학에 관한 16세기 원고이다.
• 광선의 시스템 이론 – W.R. 해밀턴 왕립 아일랜드 아카데미, 제15권, 1828년.

초기 서적과 논문의 영어 번역

• H. 브룬스, "Das Eikonal"
• M. 말루스, "Optique"
• J. 플러커, "광파의 일반적인 형태에 대한 논의"
• 쿠머, "직선계의 일반 이론"
• E. Kummer, 광학적으로 실현 가능한 직선선 시스템에 대한 프레젠테이션
• R. 메이바우어 "광선 직선계 이론"
• M. Pasch, "레이 시스템의 초점 표면과 복합체의 특이성 표면에 대하여"
• A. Levistal, "기하 광학 연구"
• F. 클라인, "브룬스 에이코날에서"
• R. 돈토, "적분 불변량과 기하학 광학 일부 점에 대하여"
• T. de Donder, "광학의 적분 불변성에 대하여"

외부 링크

• 파인만의 기하학 광학 강의