전자장 방출

자기장 전자 방출(FE)과 전자장 방출이라고도 알려진 자기장 전자 방출은 정전기장에 의해 유도된 전자의 방출이다. 가장 일반적인 맥락은 고체 표면에서 진공으로 방출되는 전기장 방출이다. 단, 현장 방출은 고체 또는 액체 표면에서 진공, 액체(예: 공기) 또는 비전도성 또는 약하게 전도성 유전체로 발생할 수 있다. 반도체의 발란스에서 전도 대역으로 전자가 자기장에 의해 촉진되는 현상(제너 효과)도 자기장 방출의 한 형태로 볼 수 있다. 이 용어는 표면 광효과, 열전 방출(또는 리처드슨-두쉬만 효과), "콜드 전자 방출(cold electronic electronic exposition)"의 관련 현상, 즉 강한 정전기장(또는 준정전기장)에서의 전자 방출이 1880년대부터 1930년대까지 독립적으로 발견되고 연구되었기 때문에 역사적이다. 한정자 없이 필드 배출을 사용할 경우 일반적으로 "콜드 배출"을 의미한다.

순수 금속의 현장 배출은 높은 전기장에서 발생한다: 그라데이션은 일반적으로 미터당 1기가볼트보다 높고 작업 기능에 따라 크게 좌우된다. 필드 방출에 기반한 전자 소스는 여러 가지 용도를 가지고 있지만, 필드 방출은 엔지니어들이 예방하기 위해 노력하는 진공 파괴와 전기 방전 현상의 가장 흔하지 않은 일차 공급원이다. 표면장 방출의 적용 예로는 고해상도 전자현미경을 위한 밝은 전자원의 구축이나 우주선에서 유도된 전하의 방전이 있다. 유도 전하를 제거하는 장치를 충전중립제라고 한다.

전기장 방출은 1920년대 후반에 전자의 양자 터널링에 의해 설명되었다. 이것은 초기 양자역학의 승리 중 하나였다. 랄프 H. 파울러와 로타 볼프강 노르드하임에 의해 벌크 금속에서 발생하는 자기장 방출 이론이 제안되었다.^[1] 대략적인 방정식인 파울러-노르드하임 방정식들의 이름을 따서 명명되었다. 엄밀히 말하면 파울러-노르드하임 방정식은 벌크 금속의 현장 배출과 (적절한 수정으로) 다른 벌크 결정 고형물의 현장 배출에만 적용되지만, 다른 물질로부터의 현장 배출량을 설명하는 데 대략적인 근사치로 종종 사용된다.

용어 및 규약

전자의 방출, 전자의 유도 전자 방출, 전자의 방출, 전자의 방출은 이 실험 현상과 그 이론의 총칭이다. 여기서 이름이 사용된다.

파울러-노르드하임 터널링은 매우 높은 전기장을 적용하여 전자 도체의 표면에 생성된 둥근 삼각형 방벽을 통해 전자를 파동 기계식 터널링하는 것이다. 개별 전자는 다양한 상황에서 파울러-노르드하임 터널링에 의해 많은 물질로부터 탈출할 수 있다.

냉전자기장전자방출(CFE)은 특정 통계적 방출체제에 부여된 명칭으로, 방출체 내 전자가 초기 내부 열역학적 평형 상태에 있고 대부분의 방출 전자가 방출체 페르미 수준에 가까운 전자 상태에서 파울러-노르드하임 터널링에 의해 탈출한다. ( 대조적으로, 쇼트키 방출체에서는, 대부분의 전자가 Fermi 수준보다 훨씬 높은 상태에서, 자기장 감소 장벽의 상단을 통해 탈출한다.) 많은 고체 및 액체 물질은 적절한 크기의 전기장을 적용하면 CFE 체제에서 전자를 방출할 수 있다.

파울러-노르드하임형 방정식은 벌크 금속의 내부 전자 상태로부터 CFE를 설명하기 위해 도출된 근사 방정식의 일종이다. 가족의 다른 구성원들은 현실에 대한 다른 정도의 근사치를 나타낸다. 터널링 장벽의 물리적으로 현실적인 모델의 경우 슈뢰딩거 방정식을 어떤 간단한 방법으로든 정확하게 해결하는 것은 원칙적으로 수학적으로 불가능하기 때문에 대략적인 방정식이 필요하다. 파울러-노르드하임 유형의 방정식이 벌크 결정 고형분 이외의 물질에서 발생하는 자기장 배출을 타당하게 기술한다고 믿을 이론적 이유는 없다.

금속의 경우 CFE 체제는 실온을 훨씬 상회하는 수준까지 확장된다. 다른 전자 방출 방식(예: "열 전자 방출" 및 "쇼트키 방출")이 있으며, 방출체의 상당한 외부 난방이 필요하다. 또한 내부 전자가 열역학적 평형 상태에 있지 않고 방출 전류가 부분적으로 또는 완전히 방출 영역에 대한 전자의 공급에 의해 결정되는 방출 체계가 있다. 이러한 종류의 비균형 방출 과정은 대부분의 전자가 터널링에 의해 탈출하는 경우 자기장(전자) 방출이라고 불릴 수 있지만, 엄격히 그것은 CFE가 아니며, 파울러-노르드하임형 방정식으로 정확하게 설명되지 않는다.

어떤 맥락(예: 우주선 공학)에서는 전자가 아닌 전자가 아닌 이온의 전계 유도 방출(전계 이온 방출)에 '전계 방출'이라는 명칭이 적용되고, 어떤 이론적 맥락에서는 '전계 방출'이 전계 전자 방출과 전계 이온 방출 모두를 포괄하는 일반적 명칭으로 사용되기 때문에 주의가 필요하다.

역사적으로 자기장 전자 방출 현상은 '아오나 효과', '자동 전자 방출', '콜드 음극 방출', '장 전자 방출', '전자기장 방출' 등 다양한 이름으로 알려져 왔다.

이 글의 방정식은 국제 수량 체계(ISQ)를 사용하여 작성된다. 이것은 SI 단위를 정의하는 데 사용되는 방정식의 합리화 미터 킬로그램 초(rmks) 시스템을 중심으로 한 현대(1970년대 이후) 국제 시스템이다. 구장배출 문헌(및 구문헌에서 방정식을 직접 베끼는 논문)은 종종 수량 ε을₀ 사용하지 않는 구식 시스템을 사용하여 일부 방정식을 작성하는 경우가 많다. 이 글에서는 그러한 모든 방정식이 현대 국제형으로 전환되었다. 분명히 하기 위해서, 이것은 항상 행해져야 한다.

작업 함수는 보통 전자볼트(eV)로 주어지며, 나노미터당 볼트(V/nm) 단위로 측정하는 것이 편리하기 때문에, 대부분의 보편 상수의 값은 여기에 eV, V, nm와 관련된 단위로 주어진다. 점점 더, 이것은 현장 배출 연구에서의 정상적인 관행이다. 그러나 여기의 모든 방정식은 ISQ 호환 방정식이며 현대 국제 시스템에서 요구하는 대로 차원적으로 일관성을 유지한다. 이들의 상태를 나타내기 위해 7개의 유의한 숫자에 범용 상수의 수치 값을 부여한다. 값은 기본 상수의 2006 값을 사용하여 도출한다.

전기장 전자 방출의 초기 역사

필드 전자 방출은 길고 복잡하고 지저분한 역사를 가지고 있다. 이 절에서는 1928년 원래의 파울러-노르드하임형 방정식의 파생까지 초기 역사를 다룬다.

돌이켜 보면, J.H. 윙클러가^[2] 1744년에 보고한 전기 방전은 CFE가 그의 전선 전극으로부터 시작했을 가능성이 있어 보인다. 그러나 의미 있는 수사는 JJ 이후까지 기다려야 했다.전자의 1897년 Thomson's[3]신분증 및 후 – 열 emission[4]과 photo-emission[5]일에서 이해될 때까지 – 그 전자 금속(오히려surface-adsorbed은 기체 분자들보다)내부에서 방출될 수 있고, 응용 분야의 부재에서 그 – 전자 금속에서 뿜어져 나오는 작품funct을 극복해야 했던 –.이온 barr이어

적어도 1913년 초에는 현장 유도 방출이 별도의 물리적 효과라는 의심을 받았다.^[6] 그러나 진공 청소와 시료 청소 기술이 크게 개선된 후에야 이 기법이 잘 확립되었다. 릴리엔펠트(주로 의료용 X선 응용을 위한 전자원에 관심이 많았던 사람)는 1922년^[7] 그가 "자동전자 방출"이라고 불렀던 효과의 실험현상학에 대한 첫 번째 명확한 영어로 발표했다. 그는 1910년경부터 라이프치히에서 이 주제에 대해 연구했다. 클린트는 이것과 다른 초기 작품들을 묘사한다.^[8][9]

1922년 이후, 특히 캘리포니아 패서디나의 캘리포니아 공과대학(칼텍)에서 밀리칸이 이끄는 ^[10]그룹과 런던의 제너럴 일렉트릭 컴퍼니에서 고슬링이 이끄는 그룹에 실험적인 관심이 높아졌다.^[11] 자동 전자 방출을 이해하려는 시도에는 직선 관계를 찾기 위해 다양한 방법으로 실험 전류-전압(i-V) 데이터를 플로팅하는 것이 포함되었다. 전류가 선형보다 전압에 따라 빠르게 증가하지만, 유형 로그(i) 대 그림. 뷔는 꼿꼿하지 않았다.^[10] Walter H. Schottky는^[12] 1923년에 그 효과가 필드 축소 장벽에 대한 열 유도 방출 때문일 수 있다고 제안했다. 그렇다면 로그(i) 대 √V의 플롯은 직선이어야 하지만, 그렇지 않았다.^[10] 또한 쇼트키의 설명은 처음에는^[7] 간과되었던 지점인 CFE에서 온도 의존도가 매우 약하다는 실험적인 관찰과는 양립할 수 없다.^[6]

C.C.에서 돌파구가 열렸다. 로리첸^[13](및^[14] J. Robert Oppenheimer 독립적으로)은 로그(i) 대 1/V의 플롯이 좋은 직선을 산출한다는 것을 발견했다. 1928년 초 밀리칸과 로리첸이^[13] 발표한 이 결과는 파울러와 노르드하임에게 알려졌다.

오펜하이머는 전자의(그 효과도 필드 이온화라고 불리는)이 i(V) 의존도가 원자의field-induced면 터널링 밀리컨과 Eyring,[10]의 발행된 실험적인 전계 방출 결과에 CFE 전자의 atomic-에서 field-induced면 터널링에 기인하다고 했고 이 의존성 발견했다 predicted[14]다.orb처럼표면의 금속 원자로 되어 있다. 대안적인 파울러-노르드하임 이론은^[1] 밀리칸-로리첸 발견과 온도에 대한 전류의 매우 약한 의존성을 모두 설명했다. 파울러-노르드하임 이론은 CFE가 현재 우리가 금속 전도 대역이라고 부르는 자유 전자 형태의 상태로부터 현장 유도 터널링에 기인하고, 페르미-디락 통계에 따라 전자 상태가 점유되어 있다면 둘 다 결과가 될 것이라고 예측했다.

오펜하이머는 그의 이론에 대한 수학적인 세부사항들이 심각하게 부정확했다.^[15] 또한 CFE 전류 밀도에 대해 파울러-노르드하임 이론이 제시한 최종 방정식에도 작은 수치 오류가 있었다: 이것은 1929년 논문 (Stern, Gosling & Fowler 1929)에서 수정되었다.^[16]

엄밀히 말하면 파울러-노르드하임 1928 이론의 장벽장이 인가 전압에 정확히 비례하고, 방출 영역이 전압과 독립되어 있다면 파울러-노르드하임 1928 이론은 형태(log(i/V²) 대 1/V)의 플롯이 정확한 직선이어야 한다고 예측한다. 그러나 현대의 실험 기법은 파울러-노르드하임 이론 결과와 밀리칸-로리센 실험 결과를 구별하기에 충분하지 않았다.

따라서 1928년까지 벌크 금속으로부터 CFE의 기원에 대한 기본적인 물리적 이해가 달성되었고, 원래의 파울러-노르드하임형 방정식이 도출되었다.

문헌에서는 흔히 파동기가 예측한 전자 터널링의 존재에 대한 증거로 파울러-노르드하임 작품을 제시한다. 이것이 맞지만, 1928년까지 파기의 유효성은 대체로 받아들여졌다. 파울러-노르드하임 논문의 더 중요한 역할은 1927년 소머펠트가^[17] 제안한 대로 페르미-디락 통계치가 금속의 전자 행동에 적용되었다는 실험에서 나온 설득력 있는 주장이라는 것이었다. 파울러-노르드하임 이론의 성공은 소머펠트 사상의 정확성을 뒷받침하는 데 많은 기여를 했으며, 현대 전자 대역 이론을 확립하는 데 큰 도움이 되었다.^[18] 특히 원래의 파울러-노르드하임형 방정식은 전자 스핀 존재의 통계적-기계적 결과를 실험 응축 물질 효과 이론에 통합한 최초의 방정식 중 하나이다. 파울러-노르드하임 논문은 또한 전기장 유도 전자 방출과 열 유도 전자 방출의 통일된 처리를 위한 물리적 기초를 확립했다.^[18] 1928년 이전에는 금속에는 두 종류의 전자인 "온도"와 "전도 전자"가 존재하며, 열 방출 전자 전류는 보온의 방출에 의한 것이지만, 전계 방출 전류는 전도 전자의 방출에 의한 것이라는 가설이 제기되었다. 파울러-노르드하임 1928년 연구는 보온체가 별도의 내부 전자 종류로 존재할 필요가 없다는 것을 시사했다: 전자는 페르미-디락 통계에 따라 점유된 단일 대역에서 나올 수 있지만, 온도 조건과 적용 분야에서는 통계적으로 다른 방식으로 방출될 수 있다.

오펜하이머, 파울러, 노르드하임의 사상은 조지 가모우(^[19]George Gamow)에 의해, 그리고 1928년 후반에 ^[20][21]핵의 방사성 붕괴 이론(알파 입자 터널링에 의해)에 의해 전개되는 중요한 자극제가 되기도 했다.^[22]

실제 적용: 과거 및 현재

현장 전자 현미경 및 관련 기초

이미 지적한 바와 같이, 전기장 전자 방출(1910–1920)^[7]에 관한 초기 실험 연구는 의료용 소형 X선 튜브를 개발하려는 릴리엔펠트의 열망에 의해 추진되었다. 하지만 이 기술이 성공하기에는 너무 이르다.

1928년 파울러-노르드하임 이론 연구 이후, 1937년 에르윈 W에 의한 개발로 큰 진전이 있었다. 구형 지오메트리 자기장 전자현미경(FEM)^[23]의 뮬러("장 방출 현미경"이라고도 함)이다. 이 계측기에서 전자 방출기는 정점 반경 r의 뾰족한 와이어다. 이것은 진공 인클로저에서 이미지 검출기(원래 인광 스크린)의 반대편인 R에 위치한다. 현미경 화면에는 일반적으로 10에서⁵ 10까지⁶ 확대된 대략적인 (R/r)의 배율과 함께 방출체 정점에 걸친 전류 밀도 J 분포의 투영 영상이 표시된다. FEM 연구에서 정점 반경은 일반적으로 100 nm에서 1 μm이다. 뾰족한 철사의 끝은 물리적인 물체로 일컬어졌을 때, "야전 방출체", "팁" 또는 (최근에) "뮬러 방출체"라고 불려왔다.

방출체 표면이 깨끗한 경우, 이 FEM 이미지는 (a) 방출체가 만들어지는 재료: (b) 니들/와이어 축에 상대적인 재료의 방향 및 (c) 어느 정도 방출체 엔드폼의 모양. FEM 영상에서 어두운 영역은 국소 업무 기능 φ이 상대적으로 높고/또는 국소 장벽 필드 F가 상대적으로 낮은 영역에 해당하므로 J가 상대적으로 낮으며, 광 영역은 φ이 상대적으로 낮고/또는 F가 상대적으로 높은 지역에 해당하므로 J가 상대적으로 높은 지역에 해당한다. 이는 파울러-노르드하임 형식 방정식의 지수에 의해 예측된 것과 같다[아래 eq. (30) 참조].

가스 원자의 층(산소 등)을 방출체 표면에 흡착하거나 그 일부가 표면의 이 부분의 국소적 작업 기능을 변화시키는 표면 전기 쌍극체를 만들 수 있다. 이는 FEM 영상에 영향을 미친다. 또한 작업 기능의 변경은 파울러-노르드하임 플롯(아래 참조)을 사용하여 측정할 수 있다. 따라서, FEM은 표면 과학의 초기 관찰 도구가 되었다.^[24][25] 예를 들어, 1960년대 FEM 결과는 이질적인 촉매변환에 대한 논의에 크게 기여했다.^[26] FEM은 표면 원자 확산 연구에도 사용되었다. 그러나 FEM은 이제 거의 완전히 새로운 표면 과학 기법으로 대체되었다.

FEM 개발 및 후속 실험의 결과, 이미터가 "청결"되었을 때 (FEM 영상 검사로부터) 식별할 수 있게 되었고, 따라서 다른 기법에 의해 확립된 것처럼 깨끗한 표면 작업 기능을 보여주었다. 이는 표준 파울러-노르드하임형 방정식의 유효성을 시험하기 위해 설계된 실험에서 중요했다.^[27][28] 이러한 실험은 텅스텐의 클린 표면 sur–값을 가정하여 파울러-노르드하임 그림(아래 참조)에서 전압-대-배리어 필드 변환 계수 β 값을 추론하고, 이를 이미터 형상과 정전기 모델링의 전자 마이크로스코프 관측치에서 도출한 값과 비교하였다. 약 10% 이내로 합의를 보았다. 잘^[29] 준비된 프로브를 잘 준비된 표면에 가깝게 가져와서 대략적인 평행 판 형상을 가정할 수 있고 변환 계수를 1/W로 취할 수 있으므로 W가 측정된 프로브 대 이미터 분리인 경우, 여기서 W는 측정된 프로브 대 이미터 분리를 의미한다. 결과 파울러-노르드하임 플롯의 분석은 방출자의 독립적으로 알려진 작업 기능에 가까운 작업 기능 값을 산출한다.

전자의 분광학(전자에너지 분석)

전기장 방출 전자의 에너지 분배 측정은 1939년에 처음 보고되었다.^[30] 1959년 영에 의해 이론적으로 실현되었고,^[31] 영과 뮬러에^[32] 의해 구면 기하학에서 측정한 양이 방출된 전자의 총 에너지 분포(그들의 "총 에너지 분포")임을 실험적으로 확인했다. 구형 기하학에서 전자는 이미터의 한 점에 대한 각운동량이 거의 보존되어 있을 정도로 이동하기 때문이다. 따라서 방출 시 방출체 표면에 평행한 방향에 있는 운동 에너지는 방사상 운동 방향과 연관된 에너지로 변환된다. 그래서 에너지 분석기에서 측정되는 것은 배출 시 총 에너지 입니다.

1960년대에 민감한 전자 에너지 분석기가 개발되면서, 총 에너지 분포의 미세한 세부 사항을 측정할 수 있게 되었다. 이것들은 표면 물리학의 미세한 세부 사항들을 반영하고 있으며, 전장 전자 분광기의 기술은 새로운 표면 과학 기법으로 대체되기 전에 한동안 번성했다.^[33][34]

전자총 공급원으로서 전자장 전자 방출체

전자현미경과 기타 전자빔 기기(전자빔 석판화에 사용되는 기기 등)에서 고해상도 달성을 위해서는 작고, 광학적으로 밝으며, 안정된 전자원에서 시작하는 것이 도움이 된다. 뮬러 방출자의 기하학적 구조에 기초한 선원은 처음 두 가지 기준에 적합하다. 개별 원자에 대한 최초의 전자현미경(EM) 관측은 1970년 크뢰, 월, 랭모어가 초기장 방출총이 장착된 스캐닝 전자현미경을 이용해 만들었다.^[35]

1950년대부터, 전자총에 사용하기 위한 필드 방출원의 개발에 광범위한 노력이 투입되었다.^[36][37][38] [예: DD53] 현장 유도 방출체 증축을 통해 또는 저기능 흡착제(일반적으로 지르코늄 산화물 – ZrO)를 a (100) 지향 텅스텐 방출체의 평평한 꼭지점에 선택적으로 증착하여 축 빔을 생성하기 위한 방법이 개발되었다.^[39]

상온에서 작동하는 공급원은 진공 시스템 벽에서 들어오는 흡착 분자로 빠르게 덮이게 되고, 방출기는 고온으로 '깜빡'해 수시로 청소해야 하는 단점이 있다. 요즘은 뮬러-배출기(Mueller-emitter) 기반 선원을 쇼트키(Schottky) 방출체나 소위 온도장 중간체제로 상승된 온도에서 운용하는 것이 더 일반적이다. 많은 현대의 고해상도 전자현미경과 전자빔 기구는 뮬러 방출체 기반의 전자 선원의 어떤 형태를 사용한다. 현재 전자총배출원으로 탄소나노튜브(CNT)를 개발하려는 시도가 이뤄지고 있다.^[40][41]

전자 광학 계기에 필드 방출원을 사용하는 것은 충전된 입자 광학의 적절한 이론의 개발 및 관련 모델링의 개발을 수반했다.^[37][42] 뮬러 배출자를 위해 다양한 형상 모델이 시도되어 왔는데, 가장 좋은 것은 트롤란 주 다이크가 선보인 'SOC(Sphere on Orthogonal Conn)' 모델인 것 같다. 1953년 돌란과 반스.^[43] SOC 방출체 모델을 사용한 궤적 추적을 포함하는 중요한 시뮬레이션은 위세너와 에버하트에 의해 이루어졌다.^[44][45][46] 오늘날, 뮬러 방출체로부터의 필드 배출을 시뮬레이션하는 시설은 전자 빔 계기를 설계하는 데 사용되는 상용 전자 광학 프로그램에 종종 통합된다. 효율적인 현대적 현장배출 전자총 설계에는 고도의 전문지식이 필요하다.

원자적으로 날카로운 방출체

오늘날에는 단일 원자로 끝나는 방출체를 포함하여 매우 날카로운 방출체를 준비하는 것이 가능하다. 이 경우 전자 방출은 단일 원자의 결정학적 크기의 약 두 배인 영역에서 발생한다. 이는 이미터의 FEM과 자기장 이온 현미경(FIM) 영상을 비교하여 입증되었다.^[47] 뮬러 방사체는 또한 스캐닝 프로브 현미경 및 헬륨 스캐닝 이온 현미경(He SIM)과도 관련이 있다.^[48] 그것들을 준비하는 기술은 수년 동안 조사되어 왔다.^[47][49] 관련된 중요한 최근의 진전은 트리머가 해체될 경우 3원자("트리머") 정점을 원래 상태로 복원하기 위한 자동화된 기법의 개발(He SIM에 사용하기 위한)이었다.^[48]

광역장 방출원: 진공 나노전자

재료 측면

광역장 배출원은 1970년대부터 관심이 모아지고 있다. 이러한 기기에서는 기질(원래 실리콘) 위에 개별적인 필드 배출 현장의 고밀도가 생성된다. 이 연구 분야는 처음에는 "진공 마이크로 전자 공학"으로, 지금은 "진공 나노 전자 공학"으로 알려지게 되었다.

원래의 두 가지 장치 유형 중 하나인 "스핀트 어레이"^[50]는 실리콘 통합 회로(IC) 제작 기법을 사용하여 몰리브덴 콘이 산화막의 작은 원통형 공극에 침전된 일반 배열을 만들었고, 이 공극은 중앙 원형 개구부로 덮였다. 이 전체적인 기하학은 또한 공허에서 자란 탄소 나노튜브와 함께 사용되어 왔다.

다른 원래 장치 유형은 "Latham emitter"^[51][52]이다. 이들은 유전체 필름에서 미립자를 전도하는 장치인 MIMIV(금속 인슐레이터-금속 인슐레이터-진공기) 또는 보다 일반적으로 CDCDV(전도체-유전체-유전체-유전체-진공)이다. 그 장치는 마이크로 구조/나노 구조물이 필드 강화 특성을 가지고 있기 때문에 필드-임피트를 한다. 이 재료는 "잉크"로 침전될 수 있다는 점에서 잠재적인 생산상 이점을 가지고 있었기 때문에 IC 제작 기법이 필요하지 않았다. 그러나 실제로 한결같이 신뢰할 수 있는 기기는 조작하기 어려운 것으로 판명되었다.

연구는 필드 강화에 적합한 특성을 가진 박막으로 퇴적/성장할 수 있는 다른 재료들을 찾기 위해 진전되었다. 평행 플레이트 배열에서_M, 플레이트 사이의 "거시성" 필드_M F는 F = V/W로 주어진다. 여기서 W는 플레이트 분리, V는 인가 전압이다. 하나의 플레이트에 날카로운 물체가 생성되면, 정점에 있는 로컬 필드 F가_M F보다 크며 F에_M 의해 관련될 수 있다.

${\displaystyle F=\gamma F_{\mathrm {M}}}$

매개변수 γ은 "장면 증강 계수"라고 불리며 기본적으로 물체의 모양에 의해 결정된다. 현장 방출 특성은 국부 필드 F에 의해 결정되므로, 물체의 γ-값이 높을수록 상당한 방출이 발생하는 F의_M 값이 낮아진다. 따라서 주어진 W 값의 경우, 상당한 방출이 발생하는 인가 전압 V가 낮아진다.

1990년대 중반부터 약 10년 동안, 혈장 퇴적 필름의 무정형 및 "다이아몬드 유사" 탄소에 대한 현장 배출에 큰 관심이 있었다.^[53][54] 그러나, 그 후에 관심이 줄어들었는데, 그 이유는 부분적으로 CNT 배출자의 도착과 부분적으로는 배출 현장이 증착 과정에서 알 수 없는 방식으로 생성된 미립자 탄소 물체와 관련될 수 있다는 증거가 나타났기 때문이다. 이는 산업 규모 생산 공정의 품질 관리가 문제가 될 수 있음을 시사했다.ic.

"^[41]매트" 형태와 "성장된 배열" 형태로 CNT 필드 방출기의 도입은 중요한 진전이었다. 그들의 신체적 특징과 가능한 기술적 적용에 대한 광범위한 연구가 진행되었다.^[40] 필드 방출의 경우 CNT의 장점은 모양 때문에 가로 세로 비율이 높은 "자연 필드 개선 객체"라는 점이다.

최근 몇 년 동안 다른 탄소 형태(예: "탄소^[55] 나노월")와 다양한 형태의 광대역 간극 반도체를 기반으로 하는 다른 형태의 박막 방출기의 개발에 대한 관심도 크게 증가했다.^[56] 개별 배출사업장의 밀도가 충분히 높은 '고밀도' 나노구조를 개발하는 것이 특별한 목적이다. 나노튜브 거미줄 형태의 나노튜브의 박막은 또한 필드 방출 전극의 개발에 사용된다.^[57][58][59] 제작 매개변수를 미세 조정하면 개별 배출 현장의 최적 밀도를 달성할 수 있다는 것을 알 수 있다.^[57] 이들 거미줄의 2개 층을 서로 수직으로 정렬시켜 만든 2층 전극은 턴온 전기장(배출전류 10μA/cm² 달성에 필요한 전기장)을 0.3V/μm까지 낮추고 안정적인 전계 방출 성능을 제공할 수 있는 것으로 나타났다.^[58]

모든 현장 배출 장치, 특히 "산업 진공 상태"에서 작동하는 장치의 공통적인 문제는 시스템의 다른 곳에서 도달하는 가스 원자의 흡착에 의해 배출 성능이 저하될 수 있고 방출체 형상은 다양한 원하지 않는 보조 프로세스에 의해 원칙적으로 유해하게 변경될 수 있다는 것이다.uc 방출된 전자가 기체 위상 원자 또는/또는 역추적 표면으로 충격을 가함으로써 생성된 이온에 의한 폭격으로서. 따라서, 중요한 산업 요구사항은 "빈약한 진공 조건에서의 견고성"이다. 이는 새로운 방출 물질에 대한 연구에 고려될 필요가 있다.

작성 당시 가장 유망한 형태의 광역장 방출원(확실히 평균 배출 전류 밀도 달성 측면에서)은 스핀들 어레이와 CNT를 기반으로 한 다양한 형태의 발생원인 것 같다.

적용들

광역장 배출원의 개발은 원래 보다 효율적이고 새로운 형태의 전자정보 디스플레이를 만들고자 하는 바람에서 비롯되었다. 이를 "야전 방출 디스플레이" 또는 "나노 방출 디스플레이"라고 한다. 여러 프로토타입이 입증되었지만,^[40] 그러한 디스플레이를 신뢰할 수 있는 상업용 제품으로 개발하는 것은 소스 특성과 직접 관련이 없는 다양한 산업 생산 문제로 인해 방해받아 왔다[En08].

다른 제안된 광역장 방출원의^[40] 적용으로는 마이크로파 생성, 공간-차량 중성화, X선 생성 및 (배열원의 경우) 다중 전자빔 석판화가 있다. 최근 '플라스틱 전자'로 향하는 폭넓은 트렌드에 맞춰 유연한 기판에 대형 면적 방출기를 개발하려는 시도도 나오고 있다.

그러한 응용 프로그램의 개발은 진공 나노 전자공학이 해야 할 임무다. 그러나 현장 배출기는 초고진공이 좋은 조건에서 가장 잘 작동한다. 현재까지 가장 성공적인 애플리케이션(FEM, FES 및 EM 총기)은 이러한 조건에서 발생하였다. 현장 방출체와 산업 진공 상태가 잘 맞지 않는다는 안타까운 사실이 남아 있으며, 그러한 조건에서 사용되는 현장 배출원의 양호한 "진공 강건성"을 신뢰성 있게 보장하는 관련 문제들은 여전히 현재 우리가 가지고 있는 것보다 더 나은 해결책(아마도 더 현명한 재료 해결책)을 기다리고 있다.

진공 파괴 및 전기 방전 현상

이미 지적했듯이, 이제 전기장 전자 방출의 가장 초기 징후는 그것이 야기시킨 전기 방전이라고 생각된다. 파울러-노르드하임 작업 후, CFE는 진공 파괴와 전기 방전 현상의 가능한 기본적인 원인들 중 하나라고 이해되었다. (관련된 상세한 메커니즘과 경로는 매우 복잡할 수 있으며, 단일 보편적 원인은 없다.)^[60] 진공 파괴가 음극에서 나오는 전자 방출에 의해 발생한다고 알려진 곳에서, 원래의 생각은 그 메커니즘이 바늘과 같은 작은 표면 돌기에서 나온 CFE라는 것이었다. 원치 않는 전계 전자 방출 전류를 발생시킬 수 있는 전극 표면을 둥글게 하고 부드럽게 하기 위해 절차를 사용하였다(그리고 있다). 그러나 Latham 등의 연구는^[51] 방출이 또한 부드러운 표면의 반도체 혼합물의 존재와 연관될 수 있다는 것을 보여주었다. 배출이 어떻게 발생하는지에 대한 물리학은 아직 완전히 이해되지 않고 있지만 이른바 '삼중합 효과'가 개입될 수 있다는 의혹이 존재한다. 자세한 정보는 라담의 책과^[51] 온라인 참고 문헌 자료에서 찾을 수 있다.^[60]

전자 소자의 내부 전자전달

어떤 전자장치에서는 한 물질에서 다른 물질로, 또는 (경사진 띠의 경우) 한 대역에서 다른 대역으로 전자전자가 전달되는 것을 파울러-노르드하임 터널링의 한 형태로 간주할 수 있는 필드 유도 터널링 프로세스에 의해 이루어진다. 예를 들어, 로데릭의 저서는 금속-반도체 접촉과 관련된 이론을 논한다.^[61]

파울러-노르드하임 터널링

소개

이 글의 다음 부분은 벌크 금속에서 발생하는 냉장 전자 방출의 기본 이론을 다룬다. 이는 둥근 삼각형 방벽을 통한 전자 터널링을 고려함으로써 (1) "탈출 확률"에 대한 공식의 도출, (2) 내부 전자 상태에 대한 통합으로 "총 에너지 분포"를 얻음, (3) 두 번째 통합으로 배출 큐렌을 얻음과 관련된 4가지 주요 단계에서 가장 잘 다루어진다.국소 장벽장 및 국소 작업 함수의 함수로서 t 밀도, (4) 이를 인가 전압의 함수로서 전류의 공식으로 변환한다. 광역 방출체에 필요한 수정된 방정식과 실험 데이터 분석 문제는 별도로 처리한다.

파울러-노르드하임 터널링(Fowler-Nordheim tunneling)은 정확하거나 둥근 삼각형 벽을 통과하는 전자의 파동 기계식 터널링이다. (1) 전자가 처음에 국부화 상태에 있을 때, (2) 전자가 처음에 강하게 국부화되지 않을 때, 그리고 이동 파동으로 가장 잘 표현될 때 두 가지 기본적인 상황을 인식한다. 벌크 메탈 전도 대역으로부터의 방출은 두 번째 유형의 상황이며, 여기서 논의되는 것은 이 사례와 관련이 있다. 또한 방호벽이 1차원(즉, 측면 구조가 없는 경우)이고, '깜짝'이나 '리소니언스' 효과를 일으키는 미세한 규모의 구조물이 없는 것으로 가정한다. 파울러-노르드하임 터널링에 대한 이 설명을 비교적 단순하게 유지하기 위해, 이러한 가정들이 필요하지만, 물질의 원자 구조는 사실상 무시되고 있다.

동기 에너지

전자의 경우, 1차원 슈뢰딩거 방정식을 형태로 쓸 수 있다.

${\displaystyle {\frac {\hbar ^{2}}{2m}}{\frac {\mathrm {d} ^{2}\Psi (x)}{\mathrm {d} x^{2}}}=\left[U(x)-E_{\mathrm {n} }\right]\Psi (x)=M(x)\Psi (x),}$

(1)

어디 Ψ())은 전자 wave-function, 거리 x의 함수인 이미터의 전기 surface,[62]ħ에서 측정한 표현된 환원 플랑크 상수입니다, m은 전자 질량, U())은 전자 가능성 에너지, 앙은 총 전자 에너지는 x-방향에서의 동작에 관련된 M()))[U(x)− 앙]은 전자라고 불린다.예술에너지^[63] M(x)은 x-방향에서 가상의 고전적 점 전자의 운동과 관련된 전자 운동 에너지의 음으로 해석할 수 있으며, 장벽에서는 양이다.

터널링 장벽의 형태는 M(x)이 M(x) > 0인 지역의 위치에 따라 어떻게 달라지는가에 따라 결정된다. 두 가지 모델은 현장 방출 이론에서 특별한 지위를 가진다: 정확한 삼각형(ET) 장벽과 쇼트키-노르드하임(SN) 장벽이다.^[64][65] 이러한 값은 각각 방정식 (2)와 (3)에 의해 주어진다.

${\displaystyle M^{\mathrm {ET} }(x)=h-eFx}$

(2)

${\displaystyle M^{\rm {SN}=h-eFx-e^{2}/(16\pi \varepsilon_{0}x),}$

(3)

여기서 h는 장벽의 제로 필드 높이(또는 축소되지 않은 높이)이며, e는 기초 양전하, F는 장벽 필드, field은 전기₀ 상수다. 관례에 따르면, 고전적인 정전기장은 음성이지만 F는 양성으로 간주된다. SN 방정식은 물리적 효과 "상관 및 교환"을 나타내기 위해 고전적인 영상 전위 에너지를 사용한다.

탈출 확률

내부에서 주어진 장벽에 접근하는 전자의 경우 탈출 확률(또는 "전송 계수" 또는 "침입 계수")은 h와 F의 함수로서 D(h,F)로 표시된다. 터널링 이론의 일차적인 목적은 D(H,F)를 계산하는 것이다. 쇼트키-노르드하임 장벽과 같은 물리적으로 현실적인 장벽 모델의 경우 슈뢰딩거 방정식은 어떤 간단한 방법으로도 정확히 해결할 수 없다. 다음과 같은 소위 "반전형" 접근법을 사용할 수 있다. 파라미터 G(h,F)는 JWKB(Jeffreys-Wentzel-Kramers-Brillouin) 적분으로 정의할 수 있다.^[66]

${\displaystyle G(h,F)=g\int M^{1/2}{\mbox{d}x,}$

(4)

여기서 적분은 장애물(즉, M > 0인 지역을 가로질러)을 가로지르며, 매개변수 g는 다음과 같은 범용 상수로 주어진다.

${\displaystyle g\,=2{\sqrt {2m}/\hbar \ 약 10.24624\;{\rm {eV}^{-1/2}}\;{\rm {nm}^{nm}-1}.}$

(5)

포브스는 프뢰만과 프뢰만에 의해 증명된 결과를 다시 짜내어, 공식적으로 1차원적인 치료법으로 D에 대한 정확한 해법이 쓰여질^[67] 수 있다는 것을 보여주었다.

${\displaystyle \,D={\frac {P\mathrm {e}^{-G}{1+P\mathrm {e}^{-G}}}$

(6)

터널링 사전 인자 P는 원칙적으로 복잡한 공간의 경로를 따라 복잡한 반복적 통합에 의해 평가될 수 있다.^[67][68] CFE 체제에서는 (정의상) G ≫ 1. 또한 단순 모델의 경우 P 1 1. 따라서 eq. (6)는 소위 단순한 JWKB 공식으로 감소한다.

${\displaystyle D\ attach P\matrm {e} ^{-G}\ \matrm {e} ^{-G}.}$

(7)

정확한 삼각형 장벽의 경우, eq. (2)를 eq. (4)에^ET 넣으면 G = bh^3/2/F가 생성된다.

${\displaystyle b={\frac {2g}{3e}}={\frac {4{\\\sqrt{2m}}}{3e\hbar }}}\{\mathrm {eV}\}}^{-3/2}\mathrm {V}\{nmathrm}}}}}.}$

(8)

이 매개변수 b는 때때로 제2의 파울러-노르드하임 상수라고 불리는 보편 상수다. 다른 형태의 장벽에 대해 우리는 글을 쓴다.

${\displaystyle G(h,F)=\nu(h,F)G^{\mathrm {ET}}}=\nu(h,F)bh^{3/2}/F,}$

(9)

여기서 ν(h,F)는 일반적으로 eq. (4)를 사용하여 수치적 통합에 의해 결정되어야 하는 보정 계수다.

쇼트키-노르드하임 장벽 보정 계수

표준 포울러-노르드하임형 방정식을 도출하는 데 사용되는 장벽 모델인 쇼트키-노르드하임 장벽은 특별한 경우다.^[69] 이 경우 보정계수 ${\$은 f_h = F/F로_h 정의되는 단일 변수_h f의 함수로서$$ F는 쇼트키-노르드하임_h 장벽의 높이를 h에서 0으로 줄이는 데 필요한 필드라고 알려져 있다. 이 필드는 다음에 의해 주어진다.

${\displaystyle \,F_{h}=(4\pi \epsilon _{0}/e^{3}h^{2}=(0.6944617\;\mathrm {nm} \\\mathrm {nm}^{-1})(h/{\rm{eV}}}}^{2}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$

(10)

매개변수 f는_h 0에서 1까지 실행되며, 0필드 높이 h의 쇼트키-노르드하임 장벽에 대해 스케일링 장벽이라고 할 수 있다.

쇼트키-노르드하임 장벽의 경우, ν(h,F)는 함수 ν(ℓ)의 특정 값 ν(f_h)에 의해 주어진다. 후자는 그 자체로 수학적 물리학의 함수로서, 주된 쇼트키-노르드하임 장벽 함수로 불려왔다. ν(ℓ)에 대한 명시적인 시리즈 확장은 J. Deane의 2008년 논문에서 도출되었다.^[70] ν(f_h)에 대한 다음과 같은 양호한 단순 근사치가 발견되었다.^[69]

${\displaystyle v(f_{h})\대략 1-f_{h}+{\tfrac {1}{6}f_{h}\ln f_{h}.}$

(11)

붕괴폭

붕괴 폭(에너지 내) d는_h 장애물 높이 h가 증가함에 따라 탈출 확률 D가 얼마나 빨리 감소하는지 측정한다. d는_h 다음과 같이 정의된다.

${\displaystyle {\frac {1}{d_{h}}=-{\frac {\mathrm {d}(\ln D)}{\mathrm {d}h}.}$

(12)

h가 d만큼_h 증가하면 탈출 확률 D는 e에 가까운 인수만큼 감소한다( ( 2.718282). 초등 모델의 경우 exact = 1과 P ≈ 1을 배치한 정확한 삼각형 장벽에 기초해 볼 때

${\displaystyle d_{h}^{\mathrm {(el)}}}={{\frac {2F}{3b{\sqrt{h}}={\frac {eF}{g{\sqrt{h}}}}}}}}.}$

보다 일반적인 표현식(12)에서 도출된 붕괴폭 d는_h "decay-width correction factor" λ에_d 의해 이것과 다르므로 다음과 같다.

${\displaystyle d_{h}=\lambda _{d}d_{h}^{{d}}}={\frac {\lambda _{d}eF}{g{\sqrt{h}}}}}.}$

(13)

일반적으로 보정 계수는 통일로 근사치를 구할 수 있다.

h가 국부적인 작업 기능 φ과 동일한 방호벽의 붕괴폭 d는_F 특별한 관심사다. 숫자적으로 이 값은 다음과 같다.

${\displaystyle d_{\mathrm {F} }={\frac {\lambda _{d}eF}{g{\sqrt {\phi }}}}\approx {\frac {eF}{g{\sqrt {\phi }}}}\approx 0.09759678\;\mathrm {eV} \,\cdot {\sqrt {\frac {1\ \mathrm {eV} }{\phi }}}\cdot {\frac {F}{1\ \mathrm {V} \ \mathrm {nm} ^{-1}}}.}$

(14)

금속의 경우 d 값은_F 일반적으로 0.2 eV 순서가 되지만 장벽 필드 F에 따라 달라진다.

평.

역사적인 메모가 필요하다. 쇼트키-노르드하임 장벽은 eq(9)에서와 같이 수정 인자가 필요하다는 생각은 1928년 노르드하임에 의해 도입되었지만, 그 인자에 대한 그의 수학적인 분석은 정확하지 않았다.^[65] 1953년 버지스, 크로이머, 휴스턴에^[71] 의해 새로운 (올바른) 기능이 도입되었고, 1956년 머피와 굿에 의해 수학이 더욱 발전되었다.^[72] 때로는 "특수장 방출 타원 함수"로 알려진 이 보정 함수는 "노르드하임 매개변수"로 알려진 수학 변수 y의 함수로 표현되었다. 최근(2006~2008년)에야 수학적으로 변수 ℓ′( = y²)를 사용하는 것이 훨씬 낫다는 것을 깨달았다. 그리고 최근에 와서야 function(uss)의 정의를 완성할 수 있게 되었다. 이 기능에 대한 정확한 직렬 확장의 유효성을 개발하고 증명함으로써(Gauss 초지하계 미분방정식의 알려진 특수 사례 솔루션에서 출발함으로써) ν(ℓ)의 정의를 완성할 수 있게 되었다. 또한 근사치(11)도 최근에야 발견되었다. 근사치(11)는 등가 복잡성의 모든 오래된 근사치를 능가하며 결국 대체될 것으로 추정된다. 이러한 최근의 발전과 그 시사점은 아마도 적절한 시기에 현장 배출 연구에 상당한 영향을 미칠 것이다.

다음의 요약은 이러한 결과를 종합한다. 적절한 높이의 적절한 행동의 장벽 상단 아래 터널링의 경우 탈출 확률 D(h,F)는 다음과 같이 공식적으로 주어진다.

${\displaystyle D(h,F)\trawth P\exp \left[-{\frac {\nu(h,F)bh^{3/2}}{F}\right],}$

(15)

여기서 ν(h,F)는 일반적으로 수치적 통합에 의해 발견되어야 하는 보정 계수다. 쇼트키-노르드하임 장벽의 특별한 경우, 분석 결과가 존재하며, 위에서 논한 바와 같이 ((h,F)은 ((f_h)에 의해 주어진다. ((f_h)에 대한 근사치(11)는 모든 기술적 목적을 위해 충분하다. 사전 인자 P도 원칙적으로 h와 (아마도) F의 함수지만 여기서 논의되는 간단한 물리적 모델의 경우 대개 근사치 P = 1을 만드는 것이 만족스럽다. 정확한 삼각 장벽은 파울러와 노르드하임의 경우와 같이 슈뢰딩거 방정식을 정확하게 해결할 수 있는 특수한 경우로서,^[1] 물리적으로 비현실적인 경우인 ν(f_h) = 1이며, P에 대한 해석적 근사치가 존재한다.

여기서 설명한 접근방식은 원래 부드럽고, 고전적으로 평탄한 평면 방출 표면에서 파울러-노르드하임 터널링을 설명하기 위해 개발되었다. 약 10~20nm까지 반경의 매끄럽고 고전적인 곡면 표면에 적합하다. 그것은 더 날카로운 반지름의 표면에 적응될 수 있지만, ν과 D와 같은 양은 표면 곡률을 설명하는 데 사용되는 매개변수의 중요한 기능이 된다. 방출체가 너무 날카로워 원자 수준의 세부사항을 무시할 수 없으며/또는 터널링 장벽이 방출체-에이펙스 치수보다 두꺼운 경우, 보다 정교한 접근법이 바람직하다.

처음에 지적했듯이, 물질의 원자구조의 영향은 여기에서 논의된 비교적 간단한 전자장 방출 처리에서 무시된다. 원자구조를 제대로 고려하는 것은 매우 어려운 문제고, 제한적인 진전만 이루어졌다.^[33] 그러나 파울러-노르드하임 터널링 이론에 대한 주요한 영향은 (실제로) 현재로는 쉽게 추정할 수 없는 양으로 eq. (15)의 P와 ν의 값을 변경하는 것이 될 것 같다.

이 모든 발언은 원칙적으로 전자가 이동파 상태에서 처리될 수 있는 (터널링 전) 도체로부터 파울러 노르드하임 터널링에 적용된다. 이 접근방식은 (대략) 전자가 처음에 방출 표면 내부에서 국부적 상태 또는 매우 가까운 상태에 있는 상황에 적용되도록 채택될 수 있지만, 이는 이 글의 범위를 벗어난다.

총 에너지 분배

방출된 전자의 에너지 분포는 방출된 전자 에너지 분포를 사용하여 방출체 표면 물리학의^[34] 측면을 조사하는 과학 실험과 전자 현미경과 같은 전자 빔 계기에 사용되는 전기장 방출원에 모두 중요하다.^[42] 후자의 경우 분포의 "폭"(에너지 내)은 빔이 얼마나 정교하게 집중될 수 있는지에 영향을 미친다.

여기서의 이론적 설명은 포브스의 접근에 따른다.^[73] 만약 ε이 방출체 페르미 수준에 상대적인 총 전자 에너지를 나타내고, K는_p 방출체 표면에 평행한 전자의 운동 에너지를 나타낸다면, 전자의 정상 에너지 ε_n(때로는 "포워드 에너지"라고도 함)은 다음과 같이 정의된다.

${\displaystyle \;\epsilon _{\mathrm {n}=\epsilon -K_{\mathrm {p}}}$

(16)

두 가지 유형의 이론 에너지 분배를 인정한다. 즉, 에너지 ε이_n 방출 직후(즉, 터널링 장벽 바로 바깥) 어떻게 분배되는지 보여주는 정상 에너지 분배(NED)와 총 에너지 ε이 어떻게 분배되는지 보여주는 총 에너지 분배. 방출체 페르미 레벨을 기준 0 레벨로 사용할 경우 ε과 ε_n 둘 다 양수 또는 음수일 수 있다.

에너지 분석 실험은 1930년대부터 현장 방출체를 대상으로 실시되어 왔다. 그러나 1950년대 후반에야 비로소 이러한 실험이 항상 총 에너지 분포를 측정한다는 것을 깨닫게 되었는데(Young and^[31] Mueller [,YM58]에 의해), 현재는 일반적으로 j(ε)로 표시된다. 이것은 또한 방출이 다른 평탄한 표면의 작은 필드 강화 돌출부에서 나오는 경우에도 사실이다(또는 거의 사실이다).^[34]

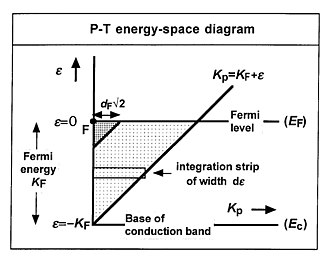
소머펠트 자유형 모델의 프레임워크 내에서 총 에너지 분포를 계산하는 방법을 보려면 P-T 에너지 공간 다이어그램(P-T="병렬-총량")을 참조하십시오.

이것은 수평축의 "병렬 운동 에너지" K와_p 수직축의 총 에너지 ε을 나타낸다. 벌크 메탈 안에 있는 전자는 대개 옅은 음영 영역 내에 있는 K와_p ε의 값을 가진다. It can be shown that each element dεdK_p of this energy space makes a contribution ${\displaystyle z_{\mathrm {S} }f_{\mathrm {FD} }\mathrm {d} {\it {\epsilon }}\mathrm {d} K_{\mathrm {p} }}$ to the electron current density incident on the inside of the emitter boundary.^[73] 여기서 z는_S 범용 상수(여기서 소머펠트 공급 밀도라고 함)이다.

${\displaystyle z_{\mathrm {S}}=4\mathrm {\pi }em/h_{\\mathrm {P}}^{3}=1.618311\time 10^{14}\,{\rm {{A}\,m^{-2}\,eV^{-2}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$

(17)

및 ${\displaystyle {F\mathrm{}}_{}}$ ${\displaystyle {\mathrm{D}}_{}}$ ${\$은(는) Fermi-Dirac 분포 함수:

${\displaystyle \,f_{\mathrm {FD}}(\epsilon )=1/[1+\exp(\epsilon /k_{\mathrm {B} }T)],}$

(18)

여기서 T는 열역학적 온도, k는_B 볼츠만의 상수다.

입사 전류 밀도의 이 요소는 다음과 같이 높이 h의 장벽이 주어진다.

${\displaystyle \,h=\phi -\epsilon +K_{\mathrm{p}}}}}$

(19a)

해당 탈출 확률은 D(h,F): 형태적으로^[73] 확장(대략)할 수 있다.

${\displaystyle D(h,F)\관련 D_{\mathrm {F}\\exp(\epsilon /d_{\mathrm {F}}\exp(-K_{\mathrm {p}{p}/d_{\mathrmatrm {F})}),}),}}}}}}$

(19b)

여기서 D는_F 국부적 작업 기능 φ과 동일한 미축소 높이의 장벽에 대한 탈출 확률이다. Hence, the element dεdK_p makes a contribution ${\displaystyle z_{\mathrm {S} }f_{\mathrm {FD} }D\mathrm {d} {\it {\epsilon }}\mathrm {d} K_{\mathrm {p} }}$ to the emission current density, and the total contribution made by incident electrons with energies in the elementary range dε is thus

${\displaystyle j(\epsilon )\mathrm {d} \epsilon =z_{\mathrm {S} }f_{\mathrm {FD} }\left[\int D\mathrm {d} K_{\mathrm {p} }\right]\mathrm {d} \epsilon =z_{\mathrm {S} }f_{\mathrm {FD} }D_{\mathrm {F} }\exp(\epsilon /d_{\mathrm {F} })\left[\int _{0}^{\infty }\exp(-K_{\mathrm {p} }/d_{\mathrm {F} })\;\mathrm {d} K_{\mathrm {p} }\right]\mathrm {d} \eps일론,}$

(20)

여기에서 적분은 원칙적으로 도표에 표시된 스트립을 따라 취하되, 붕괴폭 d가_F 페르미 에너지 K_F(항상 금속의 경우 해당)보다 훨씬 적을 때 실제로 ∞까지 확장할 수 있다. 통합의 결과는 다음과 같이 기록될 수 있다.

${\displaystyle \,j(\epsilon )=z_{\mathrm {S} }d_{\mathrm {F} }D_{\mathrm {F} }f_{\mathrm {FD} }(\epsilon )\exp(\epsilon /d_{\mathrm {F} })=j_{\mathrm {F} }f_{\mathrm {FD} }(\epsilon )\exp(\epsilon /d_{\mathrm {F} }),}$

(21)

where ${\displaystyle d_{\mathrm {F} }}$ and ${\displaystyle D_{\mathrm {F} }}$ are values appropriate to a barrier of unreduced height h equal to the local work function φ, and ${\displaystyle j_{\mathrm {F} }[\,=z_{\mathrm {S} }d_{\mathrm {F} }D_{\mathrm {F} }]}$ 이 방정식에 의해 정의된다.

주어진 이미터의 경우, 주어진 필드가 적용된 $j{\displaystyle {}_{}}$ ${\$은(는) F와 독립적이므로$$ eq.(21) 분포의 모양은 상승 지수로서 FD 분포 함수에 곱한 것이다. 이는 영이 먼저 예측한 친숙한 분포 형태를 생성한다.^[31] 저온에서 $F{\displaystyle {}_{}}$ ${\displaystyle {\mathrm{D}(}_{}}$ $){\displaystyle f_{\mathrm {FD}}}}(\epsilon )}$은(는) 페르미 수준 근처에서 1에서 0으로 급격히 변화하며$$ 분포의 FWHM은 다음과 같이 주어진다.

${\dapplaystyle \mathrm {FWHM} \,=d_{\mathrm {F}\\ln(2)\약 0.693\,d_{\mathrm {F}}}}$

(22)

실험용 CFE 총 에너지 분포가 이러한 기본 형태를 가지고 있다는 사실은 금속의 전자가 페르미-디락 통계에 복종한다는 것을 잘 실험적으로 확인하는 것이다.

냉장 전자 방출

파울러-노르드하임형 방정식

소개

파울러-노르드하임형 방정식은 J-F 형태로 벌크 금속의 전도 대역에서 내부 전자 상태로부터 방출되는 국부 전류 밀도 J를 설명하기 위해 도출된 (대략) 이론 방정식이다. 방출 표면의 일부 작은 균일한 영역에 대한 방출 전류 밀도(ECD) J는 보통 작은 영역을 특징짓는 국소 업무 기능 φ과 국소 장벽 필드 F의 함수 J((,F)로 표현된다. 급커브 표면의 경우 J는 표면 곡률을 설명하는 데 사용되는 파라미터에 따라 달라질 수 있다.

원래 파생에서 이루어진 물리적 가정 때문에,^[1] 파울러-노르드하임형 방정식은 영온에서 ECD를 설명하는 방정식에 대해서만 오랫동안 사용되어 왔다. 그러나 CFE 배출 시스템 내에서 유한한 온도에 유효한 약간 수정된 방정식(아래 설명)을 이 이름에 포함하도록 하는 것이 좋다.

영온형

전류 밀도는 A/m으로² 가장 잘 측정된다. 작은 균일 영역에서 방출되는 총 전류 밀도는 총 에너지 분배 j(ε)를 총 전자 에너지 ε에 대해 통합함으로써 얻을 수 있다. 영온에서 페르미-디락 분포 함수는 ε<0의 경우 f_FD = 1이고, f = 0은 for_FD>0의 경우 0이다. 따라서 0K, J의₀ ECD는 eq. (18)에서 다음 방법으로 주어진다.

${\displaystyle J_{0}=z_{\mathrm {S} }d_{\mathrm {F} }D_{\mathrm {F} }\int _{-\infty }^{0}\exp(\epsilon /d_{\mathrm {F} })\;\mathrm {d} \epsilon \;=\;z_{\mathrm {S} }{d_{\mathrm {F} }}^{2}D_{\mathrm {F} }\;=\;Z_{\mathrm {F} }D_{\mathrm {F} },}$

(23)

여기서 $Z{\displaystyle {}_{}}$ ${\displaystyle {F\mathrm{}}_{}{}_{}}$[${\displaystyle }$= ${\displaystyle {}_{}}$ S ${\displaystyle {d\mathrm{}}_{}}$ ${\displaystyle {{F\mathrm{}}_{}}^{}}$ ${\displaystyle {2_{}}^{\mathrm{}}}$ ${\displaystyle {}^{}}$ ${\displaystyle Z_{\mathrm {F}}\\;[=$z_${\mathrm {S}}{d_{\mathrm {F}}}}}}}}}}}}}은($는) 상태 F에 대한 유효 공급이며 이$$ 방정식으로 정의된다. 엄격히, 적분 하한은 -K여야_F 하며, 여기서_F K는 페르미 에너지여야 한다. 그러나_F d가 K보다_FF 훨씬 작을 경우(금속에 항상 해당) K 이하의 에너지에서 적분된 경우, 적분에 대한 유의한 기여는 K 이하의 에너지에서 나오지 않으며, 공식적으로 –migration까지 확장될 수 있다.

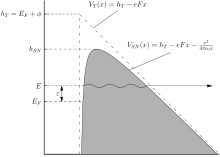
결과(23)는 그림 1을 참조하여 간단하고 유용한 물리적 해석을 제공할 수 있다. 도표("상태 F")의 점 "F"에 있는 전자 상태는 "페르미 수준에서 전방 이동 상태"(즉, 방출체 표면과 정상으로 이동하는 페르미 수준 전자를 설명한다). 0K에서 이 상태의 전자는 미감소된 높이 barrier의 장벽을 보게 되며, 다른 점유된 전자 상태의 장벽보다 높은 탈출 확률 D를_F 갖게 된다. 따라서 J를₀ ZD로_FF 표기하는 것이 편리하며, 여기서 "유효 공급" Z는_F 모든 배출물이 주 F에서 나온다면 주 F가 금속 내부에서 운반해야 하는 전류 밀도다.

실제로 전류 밀도는 주로 에너지와 주 F에 가까운 상태 그룹에서 나오며, 대부분은 에너지 공간 다이어그램에서 음영이 심한 영역 내에 있다. 자유 전자 모델의 경우 현재 밀도에 대한 기여도가 에너지 공간 내 면적(소머펠트 공급 밀도 z를_S 비례성의 상수로 하여)에 정비례하므로, 에너지 공간 다이어그램의 크기_F² d(eV로² 측정) 영역에서 전자 상태로부터 도출된 ECD를 생각해 보는 것이 유용하다. 즉, 그림 1의 음영이 짙게 드리워진 영역에 있는 상태에서 ECD를 생각해 보는 것이 유용하다(이 근사치는 온도가 상승할수록 서서히 악화된다).

Z는_F 다음과 같은 형태로도 쓸 수 있다.

${\displaystyle Z_{\mathrm {F} }=z_{\mathrm {S} }{d_{\mathrm {F} }}^{2}={\lambda _{d}}^{2}(z_{\mathrm {S} }e^{2}g^{-2})\phi ^{-1}F^{2}={\lambda _{d}}^{2}a\phi ^{-1}F^{2},}$

(24)

여기서, 때로는 First Fowler-Nordheim Constant라고 불리는 보편 상수 a는 에 의해 주어진다.

${\displaystyle a=z_{\mathrm {S} }e^{-2}g^{-2}=e^{3}/8\pi h_{\mathrm {P}}\\\time 10^{-6}\;\mathrm {A\;eV} \\\\\\\\\\\mathrmathrmathrmathrmathrmathrmathrmathrmat {V}{V}{V}}}{{{{{{{v}}}}}}}}}}}$

(25)

이것은 파울러-노르드하임 형식 방정식에 나타나는 전우량 인자 a φF가⁻¹² 자유 전자 모델에서 방출체 표면에 대한 전자의 유효 공급과 관련이 있음을 분명히 보여준다.

0이 아닌 온도

0이 아닌 온도에 유효한 결과를 얻기 위해, eq. (23)에서 zdD_SFF = J₀/d를_F 주목한다. 따라서 eq. (21)가 0이 아닌 온도에서 통합되면 - 이 대체 작업을 수행하고 Fermi-Dirac 분배 함수의 명시적 형식을 삽입할 때 - ECD J는 다음과 같은 형태로 작성될 수 있다.

${\displaystyle J=J_{0}\int _{-\infty }^{\infty }{\frac {\exp(\epsilon /d_{\mathrm {F} })}{1+\exp[(\epsilon /d_{\mathrm {F} })(d_{\mathrm {F} }/k_{\mathrm {B} }T)]}}\mathrm {d} (\epsilon /d_{\mathrm {F} })=\lambda _{T}J_{0},}$

(26)

여기서 λ은_T 적분에서 부여한 온도 보정계수다. The integral can be transformed, by writing ${\displaystyle w=d_{\mathrm {F} }/k_{\mathrm {B} }T}$ and ${\displaystyle x=\epsilon /d_{\mathrm {F} }}$, and then ${\displaystyle u=\exp(x)}$, into the standard result:^[74]

${\displaystyle \int _{-\inflt _{-\inflt _{-\inflt _{-}^{1+{e}}}}}}{{w}}}\mathrm {d}{nt}^{0}}{\frac {d}{1+u^{w}{w}{w}{w}{w.}}}}={\frac {\pi }{w\sin(\pi /w)}}.}$

(27)

이것은 w>1 (즉, d_F/kT_B > 1)에 유효하다. 따라서 kT_B(kt_F)와 같은 온도의 경우:

${\displaystyle \lambda _{T}={\frac {\pi k_{\mathrm {B} }T/d_{\mathrm {F} }}{\sin(\pi k_{\mathrm {B} }T/d_{\mathrm {F} })}}\approx 1+{\frac {1}{6}}{\frac {\pi k_{\mathrm {B} }T}{d_{\mathrm {F} }}}^{2},}$

(28)

여기서 팽창은 (πkT_B/d_F) ≪ 1. 예시 값(φ= 4.5 eV, F= 5 V/nm, T= 300 K)은 λ_T= 1.024이다. 정상적인 사고는 CFE 체제에서 λ은_T 다른 불확실성에 비해 항상 작으며, 상온에서 현재 밀도를 위해 공식에 명시적으로 포함할 필요가 없다는 것이었다.

금속의 방출 체계는 실제로 주어진 방출 방정식 계열이 수학적으로 적절한 장벽 필드 F와 온도 T의 범위에 의해 정의된다. CFE 시스템이 0K에서 금속 방출을 위해 작동할 만큼 장벽 필드 F가 높을 경우 조건 kT_B<d는_F CFE 방출을 위해 공식적인 상한(온도)을 제공한다. 그러나 (도출의 다른 곳에서 이루어진 근사치 때문에) 조건 kT_B<0_F.7d가 더 나은 작동 한계라고 주장되어 왔다. 이는 약 1.09의 λ-값에_T 해당하며 (예:) 약 1770 K의 CFE 체제에 대한 상한 온도 한계에 해당한다. 이 한계는 장벽장의 기능이다.^[33][72]

결과(28)는 어떤 형태의 장벽에도 적용된다는 점에 유의하십시오(다만_F d는 장벽마다 다르다).

물리적으로 완전한 파울러-노르드하임형 방정식

결과(23) 또한 원자 수준 효과를 고려할 때 어떤 일이 일어나는지 어느 정도 이해하게 되고, 밴드 구조는 더 이상 자유 전자가 아니다. 원자 이온 코어가 존재하기 때문에 표면 장벽과 표면의 전자파 기능도 다를 것이다. 이는 보정 계수 $\nu {\displaystyle }$ ${\displaystyle \nu$ 사전 인자 P 및 (제한된 범위까지) 보정 계수 λ의_d 값에 영향을 줄 것이다. 이러한 변화들은 차례로 파라미터 D와_F (제한된 범위까지) 파라미터 d의_F 값에 영향을 미칠 것이다. 실제 금속의 경우 에너지 공간의 위치에 따라 공급 밀도가 달라지며, 지점 "F"에서의 값은 소머펠트 공급 밀도와 다를 수 있다. 전자밴드 구조 보정계수 into를 eq. (23_B)에 도입함으로써 이러한 효과를 고려할 수 있다. 모디노스는 이 인자가 어떻게 계산될 수 있는지에 대해 토론했다. 그는 0.1과 1 사이에 있을 가능성이 가장 높다고 추정했다. 이 인자는 이 한계를 벗어날 수 있지만 0.01<10> 범위를_B 벗어날 가능성은 가장 낮다.^[75]

λ_T λ_B λ과 동일한_d² 전체 공급 보정계수 λ을_Z 정의하고, 위의 방정식을 결합함으로써 이른바 물리적으로 완전한 파울러-노르드하임형 방정식에 도달한다.^[76]

${\displaystyle J\;=\lambda _{Z}a\phi ^{-1}F^{2}P_{\mathrm {F}\exp[-\nu _{\mathrm {F}}}{b\phi ^{3/2}/F],},}}$

(29)

여기서 $\nu {\displaystyle {}_{}}$ ${\displaystyle {\mathrm{}}_{}}$ ${\$ $$${\displaystyle {\mathrm{}}_{}}$ F$${\$displaystyle${\$nu }$_{\$mathrm {$F$\}\}\}\}\}\}\}\}\}(,,$ F)은 축소되지 않은 높이의 장벽에 대한 지수 보정 계수다. 이것은 파울러-노르드하임 유형의 가장 일반적인 방정식이다. 패밀리의 다른 방정식은 $\nu {\displaystyle {}_{}}$ ${\displaystyle {\mathrm{}}_{}}$ ${\$ P_F 및 λ에_Z 포함된 세 가지 보정 인자에 대한 구체적인 표현을 대입하여 구한다. 현장배출의 학부 교과서 논의에 등장하는 이른바 초등 파울러-노르드하임식 방정식은 λ_Z→1, P_F→1, ${\displaystyle {\mathrm{}}_{}}$ F ${\$를 넣어 얻는데, 이는 물리적 현실보다 장벽을 더 강하게 만들기 때문에 좋은 양적 예측을 하지 못한다. 소위 표준Fowler–Nordheim-type 방정식, 원래 머피와 Good,[72]에 의해 훨씬 지난 문헌에서 사용하여 개발, fh의 f값 h=φ을 가함으로써 얻는 곳 vF v(f)은 F{\displaystyle{\nu}_{\mathrm{F}}}→vF,, 및 값(의 tF는 관련 있는 매개 변수 가까운톤 ν λZ→tF−2, PF→1을통합)입니다.[69]

여기에서 설명하는 보다 완전한 이론 내에서, 요인 t는_F⁻² 보정 인자의 구성요소 λ_d² [ 참조,^[67] 그리고 λ은_d² 거기서 λ으로_D 표시됨]이다. t의_F⁻² 별도 식별을 계속하는 데는 유의미한 가치가 없다.아마 현재 지식의 상태에서는 금속으로부터 CFE를 모델링한 단순한 파울러-노르드하임형 방정식에 대한 최선의 근사치는_Z →→1_F, P → 1, ${\displaystyle {\mathrm{}}_{}}$ F$${\$displaystyle {\nu}}{\mathrm {F}}}}}{\$mathrmathrmatmat {F$}$ → v($$f)를 넣어 얻을 수 있다. 이는 1956년 다이크와 돌란이 사용한 파울러-노르드하임형 방정식을 다시 생성하며, "간단화된 표준 파울러-노르드하임형 방정식"이라고 할 수 있다.

간단한 파울러-노르드하임 유형 계산에 권장되는 양식

명시적으로, 이 권고된 단순화된 표준 파울러-노르드하임 형식 및 관련 공식은 다음과 같다.

${\displaystyle J=\;a{\pi ^{-1}F^{2}\exp[-v(f)\;b\pi ^{3/2}/F],}$

(30a)

${\displaystyle a\approx \;1.541434\times 10^{-6}\;\mathrm {A\;eV} \;{\mathrm {V} }^{-2};\;\;\;\;\;b\approx 6.830890\;{\mathrm {eV} }^{-3/2}\;\mathrm {V} \;{\mathrm {nm} }^{-1},}$

(30b)

${\displaystyle v(f)\ 약 1-f+(1/6)f\ln f}$

(30c)

${\displaystyle f=\;F/F_{\phi }=(e^{3}/4\pi \epsilon _{0})(F/{\phi }^{2})=(1.439964\;{\mathrm {eV} }^{2}\;{\mathrm {V} }^{-1}\;\mathrm {nm} )(F/{\phi }^{2}).}$

(30d)

어디 Fφ 여기 현장 환원되지 않은 높이 Schottky–Nordheim한 장애물은 지역 work-function φ에 동등한 0으로 낮출 수 있으며, 환원되지 않은 키 φ의 Schottky–Nordheim 장벽을 f는 하나의 장벽 분야 필요하다 이 수량 ffφSN 더 정확히 쓰여진 있었을 수도 있지만, 이Fowler–Nordheim-type 방정식 덜 clut 보이게 만드는 것이다.tered 관례가 채택된 경우, 단순 f는 f in_φ^SN,^[69] eq. (2.16)로 표시된 양을 의미한다. 예시 사례(φ= 4.5 eV, F= 5 V/nm), f≈ 0.36 및 v(f) ≈ 0.58; 이러한 매개변수에 대한 실제 범위는 다음에서 자세히 설명된다.^[77]

변수 f(비늘어진 장벽 필드)는 과거 필드 배출 문헌에서 광범위하게 사용된 변수 y(노르드하임 매개변수)와 같지 않으며, "v(f)"는 필드 배출 문헌에 나타나는 수량 "v(y)"와 수학적 의미와 값이 같지 않다는 점에 유의한다. 여기서 설명한 개정 이론의 맥락에서 v(y)에 대한 공식과 v(y)에 대한 값 표를 무시하거나 v(f^1/2)의 값으로 취급해야 한다. v(f)에 더 정확한 값이 필요한 경우 8×10보다⁻¹⁰ 높은 절대 수학 정확도에 v(f) 값을 제공하는 공식을 제공한다^[69]. 그러나 0.0025의 절대 수학 정확도 내에서 정확한 값을 산출하는 위의 근사 공식(30c)은 모든 기술적 목적에 대해 충분히 정확한 값을 제공해야 한다.^[69]

평.

파울러-노르드하임 유형의 방정식을 도출하는 방법에 대한 역사적 참고가 필요하다. 자유 전자 이론을 사용하여 이러한 방정식을 도출하는 데는 몇 가지 가능한 접근법이 있다. 여기서 사용되는 접근방식은 2004년에 포브스가 도입했으며 "통합의 첫 번째 변수로 병렬 운동 에너지 K를_p 사용하여 총 에너지 분배를 통해 통합"이라고 설명할 수 있다.^[73] 기본적으로 '표면 브릴루인 존 위로 통합'하는 모디노스 절차^[33][75](더 진보된 양자-기계 처리에서)에 상당하는 자유 전자론이다. 이와는 대조적으로 1959년 영,^[31] 1973년^[34] 갓주크와 플럼머, 1984년 모디노스에 의한 CFE의 자유전기 치료도 ^[33]총 에너지 분배를 통해 통합되지만, 정상 에너지 ε_n(또는 관련 수량)을 통합의 첫 번째 변수로 사용한다.

또한 1928년 노르드하임의 정론적 논문에 기초하여 ^[78]문제를 다르게 형성한 다음 첫 번째_p K와 그 다음 ε_n(또는 관련 수량)을 통합 변수로 사용하는 오래된 접근법이 있는데, 이를 "정상 에너지 분배를 통한 통합"이라고 한다. 이 접근법은 일부 저자들에 의해 계속 사용되고 있다. 특히 공명 현상을 논할 때는 일부 장점이 있지만, 1단계 통합에서 페르미-디락 분배 기능의 통합이 필요하다: 비자유전자와 같은 전자 대역 구조의 경우 이는 매우 복잡하고 오류가 발생하기 쉬운 수학(반도체에 대한 스트랫튼의 작업에서와 같이)으로 이어질 수 있다.^[79] 또한 정규 에너지 분포를 통한 통합은 실험적으로 측정된 전자 에너지 분포를 생성하지 않는다.

일반적으로, 여기서 사용되는 접근법은 이해하기 쉬워 보이고, 수학의 단순화로 이어진다.

또한 첫 번째 단계는 파동 벡터 공간(k - space)^[33]의 일정한 에너지 표면에 대한 ECD에 대한 기여를 통합하거나 관련 표면 브릴루인 영역에 대한 기여를 통합하는 것이다.^[34] Forbes 접근방식은 k -space의 구형 표면에 걸쳐 통합하거나, 변수 K를_p 사용하여 방출 표면과 정상적인 방향으로 축에 대해 원통형 대칭을 갖는 고리 모양의 통합 요소를 정의하거나, 원형 링 요소를 사용하여 (확장된) 표면 브릴루인 영역에 걸쳐 통합하는 것과 동등하다.

CFE 이론 방정식

앞 절에서는 파울러-노르드하임형 방정식을 도출하는 방법을 설명한다. 엄밀히 말하면, 이 방정식은 벌크 금속의 CFE에만 적용된다. 다음 절의 아이디어는 CFE에 더 일반적으로 적용되지만, 이를 설명하기 위해 eq.(30)를 사용할 것이다.

CFE의 경우, 기본적인 이론적 치료는 방출 표면의 국소 위치에서 국소 방출 전류 밀도 J와 국소 장벽 필드 F 사이에 관계를 제공한다. 실험은 방출 표면의 정의된 일부 부분으로부터 방출 전류 i를 측정하며, 일부 역전극에 가해지는 전압 V의 함수로서 측정한다. 이러한 변수를 J와 F와 연관시키기 위해 보조 방정식을 사용한다.

전압 대 배리어 필드 변환 계수 β는 다음과 같이 정의된다.

$F=\\\beta V,}$

(31)

F 값은 방출체 표면의 위치마다 다르며, β 값은 그에 따라 달라진다.

금속 이미터의 경우, 주어진 위치에 대한 β-값은 다음과 같은 조건 하에서 일정하게(전압과 무관하게) 유지될 것이다. (1) 기기는 "다이오드" 배열이며, 여기서 존재하는 유일한 전극은 이미터와 "서라운드" 세트로서, 모든 부품이 동일한 전압에 있고, (2) 중요한 현장 장착 진공 공간 충전(F)은 없다.EVSC)이 존재함(배출 전류 밀도가 매우⁹ 높은 경우를 제외하고 10 A/m² 이상일^[27][80] 경우 제외), (3) 국소 작업 기능의 불균일성으로 인해 ^[63]유의미한 "패치 필드"가 존재하지 않는다(일반적으로 이것이 참이라고 가정하지만 일부 상황에서는 아닐 수 있음). 비금속인 경우, "장 침투"와 "밴드 벤딩"[M084]이라고 불리는 물리적 효과는 β를 인가 전압의 함수로 만들 수 있지만, 놀랍게도 이 효과에 대한 연구는 거의 없다.

방출 전류 밀도 J는 방출체 표면에 걸쳐 위치마다 다르다. 방출체의 정의된 부분으로부터의 총 방출 전류 i는 이 부분에 걸쳐 J를 통합하여 얻는다. i(V)에 대한 간단한 방정식을 얻기 위해 다음과 같은 절차를 사용한다. 기준점 "r"은 방출체 표면의 이 부분(흔히 전류 밀도가 가장 높은 지점) 내에서 선택되며, 이 기준점의 전류 밀도는 J_r. A 매개변수 A로_r 표시되며, 개념 방출 영역("r"에 대하여)은 다음으로 정의된다.

${\displaystyle i=A_{\mathrm {r} }J_{\mathrm {r} }=\int J\mathrmat {d} A,}$

(32)

이 경우, 해당 적분을 해당 방출자의 부분에 걸쳐 취합한다.

이 매개변수_r A는 1929년 스턴, 고슬링, 파울러에 의해 CFE 이론에 도입되었다(그들은 그것을 "가중 평균 영역"^[16]이라고 불렀다). 실제 방출체의 경우 파울러-노르드하임 형식 방정식에 사용되는 방출 전류 밀도는 항상 어떤 기준점에서 전류 밀도(일반적으로 명시되지 않았지만)이다. 오랫동안 확립된 규약은 위에서 사용된 첨자 "r"이 없이 단순 기호 J에 의해 이 기준 전류 밀도를 나타내고, 단순 기호 F와 β에 의한 해당 국소장과 변환 계수를 나타낸다. 다음에 나오는 규약에서는 이 규약을 사용한다.

공칭 방출 영역 A는_r 종종 기준 국부 영역(따라서 전압)의 함수가 되며,^[30] 어떤 상황에서는 온도의 중요한 함수가 될 수 있다.

A는_r 수학적 정의를 가지고 있기 때문에, 자기장 전자(배출) 현미경의 단점 방출기에서 발생하는 방출이 관찰되는 영역과 반드시 일치하는 것은 아니다. 많은 개별 배출 현장이 포함된 대형 면적 방출기의 경우, A는_r 시각적으로 관찰된 방출체의 "거시적" 기하학적 영역(A_M)보다 거의 항상 훨씬^{[clarification needed]} 작을 것이다(아래 참조).

이러한 보조 방정식을 eq(30a) 수율에 통합

$(\displaystyle i=\;)A_{\mathrm{r} }a{\phi^{-1}{\beta ^{2}V^{2}\exp[-v(f)\;b\phi ^{3/2}/\beta V],}$

(33)

이것은 I-V 형식의 단순화된 표준 파울러-노르드하임형 방정식이다. 해당 "물리학적 완전" 방정식은 λP로_ZF 곱하여 구한다.

대면적 방출체에 대한 수정된 방정식

앞 절의 방정식은 CFE 체제에서 작동하는 모든 현장 방출체에 적용된다. 그러나 추가 개발은 개별 배출사업장이 많은 광역 배출사업자에게 유용하다.

그러한 방출체의 경우, 개념 방출 영역은 시각적으로 관찰된 물리적 방출체의 겉보기 "거시" 기하학적 영역(A_M)보다 거의 항상 매우^{[clarification needed]} 작을 것이다. 차원이 없는 매개변수 α_r, 방출의 면적 효율은 다음과 같이 정의될 수 있다.

${\displaystyle A_{\mathrm {r} }=\;\alpha _{\mathrm {r}{}A_{\mathrm {M}}}}$

(34)

또한 "매크로스코픽"(또는 "평균") 방출 전류 밀도_M J(이미터의 기하학적 영역 A에_M 걸쳐 평균)를 정의할 수 있으며, 위에 사용된 기준 전류 밀도 J와_r 관련된다.

${\displaystyle J_{\mathrm {M}=\;i/A_{\mathrm {M}}=\alpha _{\mathrm {r}}}(i/A_{\mathrm {r}}}})=\mathrm {J_{mathr}}}}}}}}}}.$

(35)

이는 다음과 같은 단순화된 표준 파울러-노르드하임형 방정식의 "대면적 버전"으로 이어진다.

${\displaystyle J_{\mathrm {M}}=\alpha _{\mathrm {r}a{\pi^{-1}F^{2}\exp[-v(f)\;b\phi ^{3/2}/F],}$

(36)

${\displaystyle i=\;\alpha _{\mathrm {r}{}A_{\mathrm {M}}a{-1}{\\beta ^{2}V^{2} exp[-v(f)\;b\phi ^{3/2}/\beta V],},}},}$

(37)

이 두 방정식 모두 방출 α의_r 면적 효율을 포함한다. 주어진 방출체에 대해 이 매개변수는 일반적으로 잘 알려지지 않은 값을 가진다. 일반적으로 α는_r 서로 다른 방출 물질 간, 그리고 서로 다른 방법으로 준비되고 처리된 동일한 물질의 다른 표본 간에서 크게 다르다. 10~10⁻¹⁰⁻⁶ 범위의 값은 가능성이 있는 것으로 보이며, 이 범위를 벗어나는 값은 가능할 수 있다.

αr의 eq.(36)의 존재는 거시적 전류 밀도들은 종종 문학(일반적으로 10A/m2large-area 이미터의 많은 형태 Spindt 이외에 arrays[50])과 국소 전류 밀도에서 가장 널리 하지만 이것은 분명 일반적으로 orde 여겨진다 달라질 수 있는 실제 배출 장소에서 인용 간의 차이를 차지하고 있다.1의 r0⁹ A/m² 또는 약간 더 작을 수 있다.

광역 방출체에 관한 기술 문헌의 중요한 부분은 국소 및 거시적 전류 밀도 또는 개념적 방출 영역 A와_r 거시적 방출 영역 A 사이의_M 명확한 구분을 하지 못하거나 인용 방정식에서 매개변수 α를_r 생략한다. 해석의 오류를 피하기 위해서는 주의가 필요하다.

또한 변환 계수 β를_r 방출체와 그 주위의 전체 기하학적 구조와 관련된 "거시 부분"과 방출체 표면의 매우 국부적인 구조의 전기장 강화 능력과 관련된 "로컬 부분"으로 분할하는 것이 편리할 때도 있다. 이것은 보통 개선을 유발하는 국소 구조가 없을 때 방출 현장에 존재할 수 있는 "거시 영역_M" F를 정의함으로써 이루어진다. 이 필드 F는_M 다음과 같이 정의된 "전압 대 매크로스코픽 필드 변환 계수" β에_M 의해 인가된 전압과 관련된다.

${\displaystyle F_{\mathrm {M} }=\;\beta _{\mathrm {M}V.}$

(38)

거리 W로 분리된 두 개의 평행 플레이트로 구성된 시스템의 일반적인 경우, 그 중 하나에 생성된 방출 나노 구조물은 β_M = 1/W이다.

그런 다음 "장면 증강 계수" γ를 정의하고 다음에 의해 β_r 및 β_M 값과 관련된다.

$[\displaystyle \filename =\;F_{\mathrm {r}/F_{\mathrm {M}}=\beta _{\mathrm {r}/\beta _{\mathrm {M}}}}$

(39)

eq.(31)를 사용하면 다음과 같은 공식이 생성된다.

${\displaystyle F=\;\gamma F_{\mathrm {M}}=\beta V;}$

(40)

${\displaystyle \beta =\;\beta _{\mathrm {M}}\gamma ;}$

(41)

여기서, 일반적인 관례에 따라, 접미사 "r"가 기준점과 관련된 매개변수에서 삭제되었다. 공식은 다양한 방출체 모양, 특히 " 기둥 위의 희석"에 대해 고전적인 전기동학을 사용하여 γ의 추정을 위해 존재한다.^[81]

방정식(40)은 Fowler-Nordheim 형식 방정식의 버전이 어디에나 F ${\displaystyle {또는\mathrm{}}_{}}$ βV가 $\gamma {\displaystyle }$ ${\displaystyle {}_{}}$ M ${\$로 대체되는 경우 작성될 수 있음을 암시한다$.$ 이것은 종종 지역 방출체 나노구조물의 특성을 강화하는 분야에 주된 관심이 있는 기술 애플리케이션에서 이루어진다. 그러나 일부 과거 작업에서는 장벽 필드 F와 거시적 필드 F를_M 명확히 구분하지 못해 혼란이나 오류가 발생하기도 했다.

더 일반적으로,large-area 전계 방출기의 기술 개발에 목적이 방출 αr의 지역 효율의 가치를 증대하여, 그리고, β의 가치를 증가시키는 것은 중요한 방출이 발생하는"시작"전압을 줄이기 위해 방출의 균일성을 강화할 예정이다. 방정식(41)이 이 두가지 방법의로 끝날 수 있을 것을 보여 준다. t"고밀도" 나노구조체를 개발하거나, 또는_M β가 증가하도록 시스템의 전체 형상을 변경함으로써. 다양한 절충과 제약이 존재한다.

실제로 위에서 사용한 거시적 영역의 정의가 가장 일반적이지만, 문헌에는 특히 개별 방출체의 i-V 특성을 조사하기 위한 프로브의 사용과 관련하여 다른 (차이하게 정의된) 거시적 분야와 필드 강화 계수가 사용된다.^[82]

기술적 맥락에서 현장 배출 데이터는 종종 (F_M 또는 1/F의_M 특정 정의를 x 좌표로 사용하여 표시된다. 그러나 과학 분석을 위해서는 일반적으로 실험 데이터를 사전 조작하지 않고 원시 측정 i-V 데이터를 직접 플롯하는 것이 좋다. 그런 다음 (다양한 형태의) γ과 같은 기술 매개변수의 값은 관련 정의를 사용하여 i-V 데이터 그림의 적합 매개변수(아래 참조)에서 얻을 수 있다.

나노미터학적으로 날카로운 방출체에 대한 수정된 방정식

필드 방출 이론의 이론적 파생은 장벽이 쇼트키-노르드하임 형식을 취한다는 가정 하에 이루어진다(3). 단, 이 장벽 형식은 튜닝링 장벽의 길이와 유사한$$ 곡률 $R{\displaystyle }$ ${\displaystyle R}$의 방사체에 유효하지 않다. 후자는 작업기능과 분야에 따라 다르지만, 실용적 관심의 경우 다음 항에서 설명한 것처럼 radi > ${\$을(를) 가진 방출체에 대해 SN 장벽 근사치가 유효한 것으로 간주할 수 있다

SN 장벽 근사치의 주요 가정은 정전위기가 튜닝링 영역에서 elling$$ =${\displaystyle F}$ ${\displaystyle x}$ ${\displaystyle \Phi =Fx}$의 선형 형태를 취한다는 것이다. 만약tunnelling 지역은 길이 L{L\displaystyle}, 음<>L{\displaystyle x&lt다 후자는 따라서 경우에만 xR≪{\displaystyle x\ll R}.[83]을 열기 위해;것으로 판명되었다.L}은 tunnelling 과정을 결정한 모든){\displaystyle)}에, 따라서 만약 LR≪{\displaystyle L\ll R}eq.(1)과 초신성 SN장벽 나고 있다.근위축은 유효하다. tunnelling 확률이 측정 가능한 필드 방출량을 생성할 수 있을 정도로 높을 경우, L은 1-2nm를 초과하지 않는다. 따라서 SN 장벽은 약 수십 nm의 반지름을 가진 방출체에 유효하다.

그러나 현대의 방출체는 이보다 훨씬 더 날카로우며, 몇 nm의 순서의 반지름을 가지고 있다. 따라서 표준 FN 방정식 또는 SN 장벽을 가정한 모든 버전의 FN 방정식은 그러한 날카로운 방출체에 중대한 오류를 초래한다. 이것은 이론적으로나^[84][85] 실험적으로 확인되었다.^[86]

위의 문제는 참고문제로 다루어졌다.^[83] SN 장벽은 방출체의 곡률을 고려하여 일반화되었다. 곡률 $[\displaystyle R}$의 반지름을 가진 금속 표면 근처에 있는 정전기 전위는 다음과 같이 점증적으로 확장될 수 있음을$$ 증명할 수 있다.

$[\displaystyle \Phi(x)=Fx\왼쪽[1-{\frac {x}{R}}}+O\왼쪽({\frac {x}{R}\오른쪽)^{2}\오른쪽]{\text{}, }}}$

(42)

또한 날카로운 이미터의 이미지 전위는 평면보다 구형 금속 표면에 해당하는 이미지로 더 잘 표현된다. 모든 $O{\displaystyle }$( ${\displaystyle x}$/ ${\displaystyle R{}^{}}$) ${\displaystyle {2\mathrm{}}^{}}$ ${\$항을$$ 소홀히 한 후, 총전위 장벽은 키리차키스와 크산타키스가 발견한^[83] 형태를 취한다.

${\displaystyle M^{KX}(x)=h-eFx\left(1-{\frac {}{R}\right)-{\frac {e^{2}}:{16\pi \epsilon _{0}x(1+x/2R)}}}.}$

(43)

JWKB 근사치(4)를 이 장벽에 사용할 경우, 가모우 지수는 eq. (5)를 일반화하는 형태를 취한다.

${\displaystyle G(h,F,R)={\frac {bh^{3/2}}:{F}\왼쪽(v(f)+\omega(f){\frac {h}{eFR}\오른쪽)}$

(44)

여기서 $f{\displaystyle }$ ${\displaystyle f}$은 (30d)로 정의되고, $v{\displaystyle }$(${\displaystyle f}$ ${\displaystyle )}$ ${\$$displaystyle$ $v$$(f)}$은${\displaystyle }$(${\displaystyle \mathrm{30c})}$와 유사한 방식으로 근사하게 계산할 수 있는 새로운 기능이다$($참조에서 인쇄 실수가 있다,^[83] 여기에서 수정).

${\displaystyle \omega(f)\약간 {\frac {4}{5}-{\frac {7}{40}f+{\frac {1}{200}\log(f)}$

(45)

필드 프리 장벽 높이 $h{\displaystyle }$ ${\displaystyle h}$의 함수로서 가모 지수 식을 고려할 때$,$ 냉장 방출에 대한 방출 전류 밀도는 eq. (23)에서 얻을 수 있다. 그것은 생산된다.

${\displaystyle J=a{\frac {F^{2}}:{\phi }}}\왼쪽({\frac {1}{\lambda _{d)(f)}+{\frac {\pi }{e)FR}}\psi(f)\오른쪽)^{-2}\exp \left[-{\frac {b\phi ^{3/2}}:{F}\f}\f(v(f)+\omega(f){\frac {\phi }{e)FR}\오른쪽)\오른쪽]}$

(46)

여기서 함수 ${\displaystyle \lambda }$ ${\displaystyle d_{}}$(${\displaystyle }$f ) ${\displaystyle \da _{d}(f)}$ $및{\displaystyle }$ ${\displaystyle (}$(${\displaystyle f}$ )$${\$displaystyle \psi(f)}$은(는) 다음과 같이 정의된다$$.

${\displaystyle {\frac{1}{\frac {1}{d}(f)}-{\frac {4}{3}{3}f{\frac {\flac {}{9}-{\frac\log(f){22}}}}}}}}}}$

(47a)

그리고

${\displaystyle \frac \flog(f){5}{3}\omega(f)-{4}{3}f{3}{\frac {4}{3}-{\frac {f}{15}-{\flack {flog(f){{15}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$

(47b)

방정식(46)에서 완전성 목적을 위해 $\lambda {\displaystyle {}_{}}$ ${\displaystyle d_{}}$ ${\$는 (29) 및 (30a)와 같이 통일성에 의해 근사치되지 않지만$$, 대부분의 실제의 경우 매우 좋은 근사치라고 할 수 있다. 이와 별도로, R${\displaystyle }$→ $【\displaystyle R\to \infit 】$의 $한계$에서 등식(43), (44) 및 (46)은 표준 파울러-노르드하임 이론(3), (30a)의 해당 등식과 일치한다$.$ 이는 전자의 등식이 후자의 일반화되기 때문에 예상된다.

마지막으로 위의 분석은 L${\displaystyle }limit{\displaystyle }$ ${\displaystyle R}$ ${\displaystyle L\ll R}$ 한계에서 점증상이며,$$SN 장벽을 사용하는 표준 파울러-노르드하임 이론과 유사하다. 그러나 2차 항을 추가하면 5~20nm 범위에서 곡률 반경의 방출체가 훨씬 더 정확해진다. 더 날카로운 방출체의 경우 전류 밀도에 대한 일반적인 근사치는 없다. 전류 밀도를 얻기 위해서는 정전기 전위를 계산하고 JWKB 적분을 수치적으로 평가해야 한다. 이를 위해 과학적인 컴퓨터 소프트웨어 도서관이 개발되었다.^[87]

경험적 CFE i–V 방정식

CFE 이론 개발의 현 단계에서는 이론 CFE 방정식과 경험적 CFE 방정식을 구별하는 것이 중요하다. 전자는 응축 물질 물리학에서 유래한다. 반면에 경험적 CFE 방정식은 단순히 전압 V에 대한 전류 i의 의존성의 실제 실험 형태를 나타내려고 시도한다.

1920년대에는 실험 CFE 결과를 기술하는 것으로 가정된 반 로가리듬 방정식의 지수에 나타난 V의 힘을 찾기 위해 경험적 방정식이 사용되었다. 1928년에 이론과 실험이 합쳐져서 (가능하면, 매우 날카로운 발광자의 경우는 제외한다) 이 힘이⁻¹ V라는 것을 보여주었다. 최근 다음과 같은 경험적 CFE 방정식의 선행 조건(pre-exponential)에서 V의 힘(수치)을 찾기 위해 CFE 실험을 수행해야 한다는 의견이 제기되었다.^[88]

$(\displaystyle i=\;)CV^{\kappa }\exp[-B/V],}$

(48)

여기서 B, C, κ은 상수로 처리된다.

eq. (42)에서 는 쉽게 알 수 있다.

${\displaystyle -\mathrm {d} \ln i/\mathrm {d}(1/V)=\;\kappa V+B,}$

(49)

1920년대에 실험 기법은 κ = 0(밀리칸과 라우르티젠으로 추정)^[13]과 κ = 2(원래 파울러-노르드하임형 방정식으로 추정)의 결과를 구별할 수 없었다.^[1] 그러나 이제 dlni/d(1/V)를 합리적으로 정확하게 측정할 수 있어야 하며(잠금식 증폭기/위상 민감 검출 기법과 컴퓨터 제어 장비를 사용하여 필요한 경우), 적절한 데이터 플롯의 기울기에서 κ을 도출할 수 있어야 한다.^[50]

근사치(30b)의 발견에 따라, 벌크 금속의 CFE에서도 값 κ=2가 예상되지 않는 것이 매우 명백해졌다. 이를 다음과 같이 나타낼 수 있다. 위의 eq. (30c)를 사용하여 치수 없는 매개변수 η을 다음과 같이 정의할 수 있다.

${\displaystyle \eta =b\phi ^{3/2}/F_{\pi \epsilon _{0};(be^{3}/4\pi \epsilon _{0}}{1/2}\^{1/2}\\\\\\\\\\mathrm {eV}/2}/2}/{epi \cHI \ev}.}$

(50)

φ = 4.50 eV의 경우, 이 파라미터의 값은 4 = 4.64이다. f = F/F와_φ v(f)는 eq(30b)에 의해 주어지기 때문에 단순화된 표준인 파울러-노르드하임형 방정식(30)의 지수를 대체 형태로 작성한 후 다음과 같이 확장할 수 있다.^[69]

${\displaystyle \exp[-v(f)\;b{\phi }^{3/2}/F]\;=\;\exp[-v(f)\;\eta /f]\;\approx \;{\mathrm {e} }^{\eta }f^{-\eta /6}\exp[-\eta /f]\;=\;{\mathrm {e} }^{\eta }f^{-\eta /6}\exp[-b{\phi }^{3/2}/F].}$

(51)

변환 계수 β가 전압과 독립적일 경우, 매개변수 f는 대체 정의 f = V/V를_φ 가지며, 여기서 V는_φ 특정 실험 시스템에서 필요한 전압으로, 쇼트키-노르드하임 장벽의 높이를 φ에서 0으로 감소시킨다. 따라서 이론 방정식의 지수(30)에 있는 인자 v(f)는 경험적 방정식의 전우량에서 추가적인 V 의존성을 발생시킨다는 것은 분명하다. 따라서 (쇼트키-노르드하임 장벽으로 인한 효과와 φ=4.5 eV의 방출자에 대해) 다음과 같은 예측을 얻는다.

$\displaystyle \kappa \약 2-\eta /6=2-0.77=1.23]}$

(52)

다른 요인들에 한Fowler–Nordheim-type 방정식에 아르곤 area[30] 공칭 방출 특히 로컬 work-function에 때문에 역시 있을 지도 모르전압 의존, 반드시 지역 work-function 4.5eV의 금속으로 κ=발표했는데 값이 있지만 당연히 아무런 이유가 그것을 기대할 수 있CFE을 위해 그 κ 예정이죠.것이다 원래 파울러-노르드하임 값 κ = 2이다.^[89]

이 제안에 대한 첫 번째 실험 테스트는 커크에 의해 수행되었는데, 커크는 약간 더 복잡한 형태의 데이터 분석을 사용하여 그의 변수 κ에 대한 값 1.36을 찾아냈다. 그의 매개변수 κ은 여기서 사용된 매개변수 κ과 매우 유사하지만, 완전히 같지는 않지만, 그럼에도 불구하고 그의 결과는 이러한 형태의 분석의 잠재적인 유용성을 확인하는 것으로 보인다.^[90]

경험적 누적합[CFE] 방정식의 사용(42)과 κ의 측정은 비금속일 경우 특히 유용할 수 있다. 엄밀히 말하면 파울러-노르드하임 유형의 방정식은 벌크 결정 고체의 전도 대역에서 나오는 배출에만 적용된다. 그러나 (42) 형식의 경험적 방정식을 모든 재료에 적용해야 한다(그러나, 매우 날카로운 방출체에 대해서는 개조가 필요할 수 있다). 새로운 재료에 대한 CFE 방정식이 파울러-노르드하임 유형의 방정식과 다를 수 있는 한 가지 방법은 이러한 CFE 방정식이 그 이전 우수성에서 다른 F(또는 V)의 힘을 가질 수 있다는 것이다. κ의 측정은 이것에 대한 실험적인 지표를 제공할 수 있다.

파울러-노르드하임 플롯과 밀리칸-로리센 플롯

파울러와 노르드하임에^[1] 의해 도출된 원래의 이론 방정식은 지난 80년 동안 실험 CFE 데이터가 구성되고 분석되는 방식에 영향을 주었다. 매우 널리 사용되는 파울러-노르드하임 플롯에서는 1929년 스턴 외 연구진이 소개한 바와 같이 ^[16]ln{i/V²}의 양이 1/V에 대해 플롯된다. 원래의 생각은 (원래 또는 기초적인 파울러-노르드하임형 방정식으로 예측한 바와 같이) 이것이 정확한 경사 S_FN. S는_FN 다음과 같은 방법으로 i-V 형태의 파울러-노르드하임형 방정식의 지수에 나타나는 매개변수와 관련이 있을 것이라는 것이었다.

${\displaystyle S_{\mathrm {FN}}=\-b{\phi }^{3/2}/\beta .}$

(47)

따라서 φ에 대한 지식은 β를 결정하거나 그 반대로 결정할 수 있을 것이다.

[원리적으로 국부적 자기장 향상 나노구조물이 존재하고 거시적 변환 계수 β를_M 결정할 수 있는 시스템 기하학에서, β에 대한 지식은 β = β/β_M 공식으로부터 이미터의 유효 자기장 증강 계수 β 값을 결정하도록 허용한다. 판 분리 W(그래서 β_M = 1/W)가 있는 2-플레이트 배열의 한 판에 생성된 필름 방출기의 일반적인 경우

$\displaystyle \gamma =\;\beta W.}$

(48)

오늘날 이것은 파울러-노르드하임 플롯의 가장 유력한 적용 분야 중 하나이다.]

이후 위의 원래의 생각은 평평한 방출체와 정확한 삼각형 장벽의 물리적으로 비현실적인 상황에 대해서만 엄격히 옳다는 것이 명백해졌다. 실제 방출체와 실제 장벽의 경우 수정된 공식을 산출하는 "슬로프 보정 계수"가_FN 도입되어야 한다.

${\displaystyle S_{\mathrm {FN}}=\;-\sigma _{\mathrm {FN}{b{\phi }^{3/2}/\beta .}}$

(49)

σ의_FN 값은 원칙적으로 전압 의존성이 있는 i(V)에 대한 물리적으로 완전한 파울러-노르드하임형 방정식의 어떤 파라미터의 영향을 받는다.

현재 중요한 것으로 간주되는 파라미터는 장벽 모양과 관련된$$ 보정계수 ${\displaystyle {factor\mathrm{}}_{}}$ F ${\$ {$F} }}$뿐이며, 잘 확립된 세부 이론이 있는 장벽은 쇼트키-노르드하임 장벽뿐이다. 이 경우 σ은_FN s라는 수학적 함수에 의해 주어진다. 이 함수 s는 1953년 버지스, 크로이머 및 휴스턴에 의해 (Nordheim 매개변수 y의 함수로서) 처음으로 정확하게 표로 작성되었으며,^[71] 쇼트키-노르드하임 장벽에 대한 스케일링 장벽 필드 f의 함수로 s를 제공하는 현대적 처리가 제공된다.^[69] 그러나 실제 이미터 작동의 경우 s 값이 0.9 - 1 범위에 있다는 것은 오래 전부터 명백했다.

실제로, 기울기 보정 계수를 세부적으로 고려하는 데 수반되는 추가적인 복잡성 때문에, 많은 저자들(실제)이_FN = = 1을 eq. (49)에 넣었고, 따라서 β 및/또는 γ의 추정치에 체계적 오차를 발생시켰으며, 이는 보통 5% 정도로 생각된다.

그러나 Fowler-Nordheim형 방정식보다 더 일반적인 경험적 방정식(42)은 필드 방출 i-V 데이터를 분석하는 새로운 방법을 제공한다. 일반적으로 경험적 방정식의 변수 B는 전자 터널링에 의해 보이는 일부 특성 장벽의 비축소 높이 H와 관련이 있다고 가정할 수 있다.

${\displaystyle B=\;bH^{3/2}/\beta .}$

(50)

(대부분의 경우, 반드시 전부는 아니지만, H는 국부적인 작업 기능과 동일할 것이다. 확실히 금속의 경우 해당된다.) 문제는 실험을 통해 B의 가치를 어떻게 결정하느냐다. (1) 두 가지 분명한 방법이 있다. (1) eq. (43)를 사용하여 [-dln{i}/d(1/V) 대 V] 형식의 플롯의 기울기에서 κ의 합리적으로 정확한 실험 값을 결정할 수 있다고 가정한다. 이 경우 ln(i)/V^κ 대 1/V의 두 번째 그림은 경사 -B의 정확한 직선이어야 한다. 이 접근방식은 B를 결정하는 가장 정확한 방법이어야 한다.

(2) 대안으로 κ의 값을 정확히 알 수 없고, 정확하게 측정할 수 없지만, 추정하거나 추측할 수 있다면, B의 값은 형식[ln{i} 대 1/V]의 플롯에서 도출할 수 있다. 이것은 1928년 밀리칸과 로리센이 사용한 플롯의 형식이다. 재배열 eq. (43) 제공

${\displaystyle B=\;-\mathrm {d} \ln(i)/\mathrm {d}(1/V)-\kappa(1/V)}$

(51)

따라서, B는 충분한 근사치로, 1/V의 일부 범위에 걸쳐 밀리칸-로리센 그림의 평균 기울기를 결정하고, 보정을 적용하여 범위의 중간점에서 1/V의 값과 κ의 가정된 값을 사용하여 결정할 수 있다.

밀리칸-로리센 플롯을 사용할 때의 주요 이점과 파울러-노르드하임 플롯과 경사 보정계수가 아닌 이러한 형태의 보정 절차는 다음과 같이 보인다.(1) 플로팅 절차는 약간 더 간단하다. (2) 보정에는 a가 아닌 측정된 수량인 물리적 파라미터(V)가 포함된다. 는[주문에, 더 일반적으로(f)σFN s의 값을(f)를 계산하기]계산되어야 한다 물리적 매개 변수(f).(3)둘 다 매개 변수, 그리고 Fowler–Nordheim-plot 등가물보다 수정 절차, 더 투명한(그리고 더 쉽게 이해가)자체 κ.(4)이 절차에 influenc 모든 신체적 영향이 걸린다.e κ의 값, 반면에 파울러-노르드하임 플롯 보정 절차(지난 50년간 수행된 형태)는 장벽 모양과 관련된 효과만을 고려한다. 더 나아가 이 모양이 쇼트키-노르드하임 장벽의 효과라고 가정한다. (5) 이론적 및 기술적 측면의 더 깨끗한 분리가 있다.ical 관심사: 이론가들은 CFE 이론에 대해 measured의 측정값이 제공하는 정보를 확립하는 데 관심이 있을 것이다. 그러나 실험자들은 단순히 κ의 측정값을 사용하여 필드 강화 인자의 더 정확한 추정(필요한 경우)을 할 수 있다.^{[citation needed]}

밀리칸-로리첸 플롯에 대한 이 보정 절차는 κ의 충분한 수의 측정이 이루어졌을 때 적용하기가 더 쉬워질 것이며, 실제 일반적인 값이 무엇인지 더 나은 아이디어를 얻을 수 있을 것이다. 현재 대부분의 재료는 -1[3] 범위에 있을 가능성이 있어 보인다.^{[citation needed]}

추가 이론 정보

위의 금속으로부터 CFE의 근사 이론을 개발하는 것은 다음과 같은 이유로 비교적 쉽다. (1) 소머펠트의 자유전기 이론은 에너지 내 내부 전자 상태 분포에 관한 그것의 특별한 가정과 함께 첫 번째 근사로서 많은 금속들에 적절하게 적용된다. (2) 대부분의 경우 금속은 표면의 sta가 없다.테스와 (많은 경우) 금속파장 기능에는 유의미한 "표면 공명"이 없다. (3) 금속은 페르미 수준에서 상태 밀도가 높기 때문에 외부 전기장을 발생/감소하는 전하가 주로 상위 원자층 외부에 있고, 의미 있는 "장 침투"가 일어나지 않는다. (4) 금속은 전도율이 높다.ty: 금속 방출체 내부에서 유의한 전압 강하가 발생하지 않음: 이는 방출 표면으로의 전자의 공급을 방해하는 요인이 없다는 것을 의미하며, 이 영역의 전자는 유효한 국소 열역학적 평형 상태와 위의 금속 지지 구조에서 전자와 효과적인 열역학적 평형 상태 둘 다일 수 있다는 것을 의미한다. (5) 원자 수준 효과는 무시된다.^{[citation needed]}

자기장 전자 방출에 대한 "단순한" 이론의 개발, 특히 파울러-노르드하임형 방정식의 개발은 위의 다섯 가지 요인 모두 참에 의존한다. 금속 이외의 물질(그리고 원자적으로 날카로운 금속 방출체의 경우)의 경우, 위의 요인 중 하나 이상이 사실이 아닐 것이다. 예를 들어 결정 반도체는 자유 전자와 같은 대역 구조를 가지고 있지 않으며, 표면 상태가 있고, 자기장 침투와 밴드 휨을 따르며, 벌크 밴드의 표면 영역에서 전자 분포로부터 표면 상태 전자 분포의 내부 전압 강하와 통계적 디커플링을 모두 나타낼 수 있다.(이 디커플링은 "모디노스 효과"로 알려져 있다.)^[33][91]

실제로 실제 파울러-노르드하임 터널링 공정의 이론은 모든 재료에 대해 거의 동일하다(방벽 모양에 대한 세부 사항은 다를 수 있으며, 변형된 이론은 이동파형이라기보다는 국부화된 초기 상태에 대해 개발되어야 한다). 그러나 그러한 차이에도 불구하고 모든 CFE 방정식이 일반적으로 유사한 방식으로 작용하는 지수를 가질 것으로 예상한다(열역학적 평형 상황에 대한). 여기서 주어진 파생의 범위를 벗어난 재료에 파울러-노르드하임형 방정식을 적용하는 일이 자주 일어나는 이유다. 관심이 파울러-노르드하임 또는 밀리칸-로리센 그림의 기울기와 CFE 방정식의 지수와 관련된 매개변수(예: 필드 강화 인자)에만 있다면 파울러-노르드하임 유형 이론은 종종 합리적인 추정치를 제시할 것이다. 그러나 의미 있는 전류 밀도 값을 도출하려는 시도는 대개 또는 항상 실패한다.

파울러-노르드하임 또는 밀리칸-로리첸 플롯의 직선은 해당 물질의 방출이 파울러-노르드하임 유형의 방정식에 따른다는 것을 나타내지 않는다는 점에 유의하십시오. 이는 개별 전자에 대한 방출 메커니즘이 아마도 파울러-노르드하임 터널링일 것임을 나타낼 뿐이다.^{[citation needed]}

서로 다른 물질은 내부 전자 상태의 에너지에서 근본적으로 다른 분포를 가질 수 있으므로, 내부 전자 상태에 대한 전류 밀도 기여를 통합하는 과정은 서로 다른 종류의 물질에 대해 전류 밀도 전우량들에 대해 현저하게 다른 표현을 발생시킬 수 있다. 특히, 전우량에서 나타나는 장벽 분야의 힘은 원래의 파울러-노르드하임 값 "2"와 다를 수 있다. 이런 종류의 효과에 대한 조사가 활발한 연구 주제다. 원자 수준의 "보복" 효과와 "스캐터링" 효과가 발생하면 이론도 수정될 것이다.

재료가 자기장 침투와 밴드 휨을 받는 경우, CFE의 상세한 이론이 개발되기 전에 (각 등급의 재료에 대해) 그러한 효과에 대한 좋은 이론을 갖는 것이 필요한 예비이다. 전압 강하 효과가 발생하는 경우 방출 전류 이론은 더 크거나 덜한 범위에서 내부 전송 효과를 수반하는 이론이 될 수 있으며, 매우 복잡해질 수 있다.

참고 항목

• 현장배출현미경
• 현장배출 탐침
• 필드 이미터 배열
• 현장 배출 디스플레이
• 프란츠-켈디시 효과

참조

추가 읽기

일반 정보

• W. Zhu, ed. (2001). Vacuum Microelectronics. Wiley, New York.
• G.N. Fursey (2005). Field Emission in Vacuum Microelectronics. Kluwer Academic, New York. ISBN 0-306-47450-6.

현장 침투 및 밴드 벤딩(반도체)

• Seiwatz, Ruth; Green, Mino (1958). "Space Charge Calculations for Semiconductors". Journal of Applied Physics. 29 (7): 1034. Bibcode:1958JAP....29.1034S. doi:10.1063/1.1723358.
• A. 다수, Y. 골드스타인, N.B. 그로버, 반도체 표면(North Holland, Amsterdam, 1965)
• W. Mönsch, Semiconductor Surface and Interface(스프링어, 베를린, 1995년)
• Peng, Jie; Li, Zhibing; He, Chunshan; Chen, Guihua; Wang, Weiliang; Deng, Shaozhi; Xu, Ningsheng; Zheng, Xiao; Chen, GuanHua; Edgcombe, Chris J.; Forbes, Richard G. (2008). "The roles of apex dipoles and field penetration in the physics of charged, field emitting, single-walled carbon nanotubes". Journal of Applied Physics. AIP Publishing. 104 (1): 014310–014310–12. arXiv:cond-mat/0612600. Bibcode:2008JAP...104a4310P. doi:10.1063/1.2946449. ISSN 0021-8979. S2CID 53453404.

현장 방출 진공 공간 충전

• Barbour, J. P.; Dolan, W. W.; Trolan, J. K.; Martin, E. E.; Dyke, W. P. (1953). "Space-Charge Effects in Field Emission". Physical Review. 92 (1): 45–51. Bibcode:1953PhRv...92...45B. doi:10.1103/PhysRev.92.45.

고온에서의 현장배출 및 광장배출

• Jensen, Kevin (2007). Electron emission physics. Advances in Imaging and Electron Physics. Vol. 149. San Diego: Academic Press. ISBN 978-0-12-374207-0. OCLC 647688316.

전자에 의한 폭발성 전자 방출

• G.A. 메시아트, 폭발성 전자 방출(URO Press, Ekaterinburg, 1998),