표면확산

표면 확산은 고체 물질 표면에서 아다톰, 분자, 원자 군집(입자)의 운동을 수반하는 일반적인 과정이다.^[1]이 과정은 일반적으로 그림 1과 같이 표면의 인접 흡착 부위들 사이에서 점핑하는 입자의 관점에서 생각할 수 있다.대량 확산에서와 마찬가지로, 이 동작은 일반적으로 온도가 증가함에 따라 속도가 증가하는 열 촉진 과정이다.많은 시스템이 가장 가까운 점프의 기존 모델에서 벗어나는 확산 동작을 나타낸다.^[2]터널링 확산은 수소가 양자 터널링 효과를 통해 깨끗한 금속 표면에 확산되는 것을 보여 주는 파격적인 메커니즘의 특히 흥미로운 사례다.

표면 확산 메커니즘과 비율을 설명하기 위해 다양한 분석 도구를 사용할 수 있으며, 그 중 가장 중요한 것은 현장 이온 현미경과 스캐닝 터널링 현미경이다.^[3]원칙적으로 그 과정은 다양한 재료에서 일어날 수 있지만, 대부분의 실험은 결정 금속 표면에서 행해진다.실험적인 제약조건 때문에 표면 확산에 대한 대부분의 연구는 기질 용해점 이하에 한정되어 있으며, 이러한 과정이 높은 온도에서 어떻게 이루어지는지에 대해서는 아직 많은 것이 발견되지 않았다.^[4]

표면 확산률과 메커니즘은 표면-입자 결합 강도, 표면 격자 방향, 표면 종과 화학적 잠재적 경도 사이의 인력과 반발력을 포함한 다양한 요인에 의해 영향을 받는다.그것은 표면 위상 형성, 상피 성장, 이질적인 촉매변환, 그리고 표면 과학의 다른 주제들에서 중요한 개념이다.^[5]이처럼 화학 생산과 반도체 산업에는 표면 확산의 원칙이 매우 중요하다.이러한 현상에 크게 의존하는 실제 애플리케이션에는 촉매변환기, 전자기기에 사용되는 집적회로, 사진 필름에 사용되는 은빛 할로겐화염 등이 포함된다.^[5]

키네틱스

표면 확산 운동학은 2D 격자의 흡착 현장에 상주하는 아다톰의 관점에서 점프 프로세스에 의해 인접 (가장 가까운) 흡착 사이트 사이를 이동한다고 생각할 수 있다.^[1][6]점프 속도는 시도 빈도와 성공적인 점프를 이끌어내는 열역학 인자가 특징이다.시도 빈도 ν은 일반적으로 아달톰의 진동 주파수인 반면 열역학적 인자는 온도와 확산에 대한 잠재적 에너지 장벽인 E에_diff 의존하는 볼츠만 인자로 간주된다.방정식 1은 다음과 같은 관계를 설명한다.

${\displaystyle \Gamma =\nu e^{-E_{\mathrm {diff} }/k_{B}T}\qquad {\text{(eq. 1)}}$

여기서 ν과 E는_diff 위에서 설명한 대로 점프 또는 깡충깡충 뛰기 속도, T는 온도, k는_B 볼츠만 상수다.E는_diff 확산이 일어나도록 탈착의 에너지보다 작아야 하며 그렇지 않으면 탈착 과정이 지배할 것이다.중요한 것은 등식 1이 기온에 따라 점프 속도가 얼마나 강하게 변화하는지 알려준다는 점이다.확산이 일어나는 방식은 열역학 인자에 주어진 E와_diff kT의_B 관계에 따라 달라진다: E_diff < kT_B>가 단결에 접근하고 E가_diff 확산의 의미 있는 장벽이 되는 것을 중단하면.이동 확산이라고 알려진 이 경우는 비교적 드물며, 몇몇 시스템에서만 관찰되었다.^[7]이 글 전반에 걸쳐 기술된 현상에 대해서는 E_diff >> kT와_B 따라서 γ << ν>로 가정한다.피키안 확산의 경우 확산계수 D 대 1/T의 로그의 아르헤니우스 그림에서 ν과 E를_diff 모두 추출할 수 있다.둘 이상의 확산 메커니즘이 존재하는 경우(아래 참조), 서로 다른 프로세스 간의 상대적 분포가 온도에 따라 변경될 수 있는 E가_diff 둘 이상일 수 있다.

무작위 보행 통계는 점프 횟수 N과 점프 a당 거리를 기준으로 확산종의 평균 제곱 변위를 설명한다.점프 성공 횟수는 간단히 Ⅱ에 확산 허용 시간을 곱한 t이다.가장 기본적인 모델에서는 가장 가까운 근처 점프만 고려되며 가 가장 가까운 흡착 지점 사이의 간격에 해당한다.평균 제곱근 변위는 다음과 같다.

${\displaystyle {\sqrt {\langle \Delta r^{2}\\angle }}}=a{\sqrt{\Samma t}}\qquad{\text{(eq. 2)}}}}}}$

확산 계수는 다음과 같이 주어진다.

${\displaystyle D={\frac {\Gamma a^{2}}:{z}\qquad {\text{(eq. 3)}}}}$

여기서, 채널 내 확산의 경우처럼$$ ${\displaystyle \mathrm{1D}}$ 확산의 경우 $z{\displaystyle }$ ${\displaystyle =}$ 2 $[\displaystyle z=2},$ 2D 확산의 $경우$ ${\displaystyle \mathrm{z}}$= 4 ${\displaystyle z=4},$ ${\displaystyle \mathrm{3D}}$ 확산의 경우$$ $z{\displaystyle }$= 6 ${\displaystyle z=6}.$^[8]

정권

확산이 일어날 수 있는 네 가지 다른 일반적인 계획이 있다.^[9]추적기 확산과 화학적 확산은 표면에서 흡착제 커버리지 수준이 다르며, 내인적 확산과 질량 전달 확산은 확산 환경의 특성에서 차이가 있다.추적 확산과 내적 확산은 모두 입자가 상대적으로 균일한 환경을 경험하는 시스템을 말하는 반면 화학적 및 질량 전달 확산 입자는 주변 환경에 의해 더 강하게 영향을 받는다.

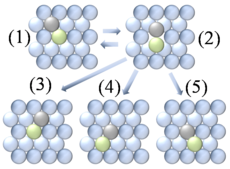
• 추적 확산은 상대적으로 낮은 커버 수준에서 표면에서 개별 입자의 움직임을 설명한다.이러한 낮은 수준(< 0.01 단열재)에서는 입자 상호작용이 낮으며 각 입자는 다른 입자와 독립적으로 움직이는 것으로 간주할 수 있다.그림 1에서 확산되는 단일 원자는 추적기 확산의 좋은 예다.
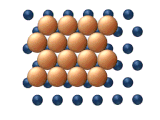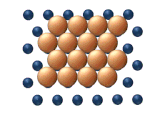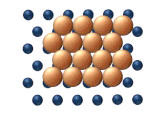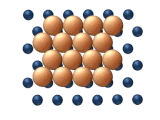
• 화학적 확산은 아다톰 사이의 끌어당김이나 반발의 영향이 중요해지는 커버리지의 높은 수준에서 과정을 설명한다.이러한 상호작용은 아다톰의 이동성을 변화시키는 역할을 한다.조잡한 방법으로, 그림 3은 아다톰이 더 높은 커버리지 수준에서 어떻게 상호작용할 수 있는지를 보여주는 역할을 한다.애덤은 처음에는 오른쪽으로 이동하는 것 외에 "선택"이 없으며, 인접한 애덤은 서로 흡착 사이트를 차단할 수 있다.
• 내적 확산은 단일 테라스 같은 균일한 표면(예: 스텝이나 빈 공간 부족)에서 발생하며, 아도톰 트랩이나 선원이 존재하지 않는다.이 체제는 종종 필드 이온 현미경을 사용하여 연구되는데, 테라스에서 테라스에서는 부분자가 확산되는 날카로운 샘플 팁이 있다.깨끗한 테라스의 경우에도 테라스의 가장자리 부근에 균일하지 않은 것이 공정에 영향을 미칠 수 있다.
• 덩어리 전이 확산은 부분자 발생원과 꼬임, 계단, 공실 등의 트랩이 있는 경우에 발생한다.점프 전위 장벽 E에만_diff 의존하는 것이 아니라, 이 체계의 확산도 이제 이동식 애드파티클의 형성 에너지에 의존한다.따라서 Teras Ledge Kink 모델에 설명된 바와 같이 Additicle의 형성에너지가 표면 형상 유형별로 다르기 때문에 확산 속도를 지시하는 역할을 한다.

애니소트로피

방향 음이소트로피는 특정 물질의 다양한 표면 방향에서 확산 속도와 메커니즘 모두의 차이 형태를 취한다.주어진 결정 물질의 경우 각 밀러 지수 평면은 고유한 확산 현상을 표시할 수 있다.FCC(111)와 같이 촘촘한 포장 표면은 FCC(100)와 같이 동일한 소재의 "개방형" 면보다 확산 속도가 더 높은 경향이 있다.^[10][11]

방향 음이소트로피(direction anisotropy)는 주어진 결정면에서 특정 방향의 확산 메커니즘 또는 비율의 차이를 말한다.이러한 차이는 표면 격자(예: 직사각형 격자) 내 음이소트로피 또는 표면의 층계 존재의 결과일 수 있다.방향성 음이소트로피의 더 극적인 예 중 하나는 채널을 따라 확산하는 것이 채널 전체의 확산보다 훨씬 빠른 FCC(110)와 같은 채널 표면에서의 아다톰 확산이다.

메커니즘

그림 4.사각형 표면 격자(파란색)에서 아돔(핑크색)과 표면 원자(은색) 사이에 발생하는 원자 교환 메커니즘 모델.표면 원자는 아원자(adatom)가 된다.공간적 또는 시간적 기준으로 확장하지 마십시오.

그림 5.공실 메커니즘을 통해 발생하는 표면 확산 모델표면 커버리지가 거의 완성되면 공실 메커니즘이 지배적이다.공간적 또는 시간적 기준으로 확장하지 마십시오.

아도톰 확산

아다톰의 확산은 다양한 메커니즘에 의해 발생할 수 있다.그들이 확산하는 방법은 다른 변수들 중에서 이동, 온도 의존성 및 표면 종의 전반적인 이동성을 지시할 수 있기 때문에 중요하다.다음은 이러한 프로세스 중 가장 중요한 프로세스에 대한 요약이다.^[12]

• 깡충깡충 뛰거나 뛰는 것은 개념적으로 아다툼의 확산을 위한 가장 기본적인 메커니즘이다.이 모델에서 아다톰은 표면 격자의 흡착 부위에 위치한다.동작은 인접한 사이트로 연속적으로 점프를 통해 발생하며, 그 수는 표면 격자의 특성에 따라 달라진다.그림 1과 그림 3은 모두 호핑 과정을 통해 확산되는 아다톰을 보여준다.연구들은 흡착 사이트들 사이에 측정 가능한 전이 상태가 존재한다는 것을 보여주었다. 여기서 아답톰은 일시적으로 존재할 수 있다.^[13]
• 원자 교환은 표면 격자 내의 아돌마와 인접 원자 사이의 교환을 포함한다.그림 4에서 보듯이, 원자 교환 사건 이후 아달톰은 표면 원자를 대신하여 표면 원자가 변위되어 현재 아달톰이 되었다.이 과정은 이질투과(예: Ni의 Pt 격자)와 자가투과(예: Pt 격자) 모두에서 발생할 수 있다.원자 교환 메커니즘이 왜 다른 시스템보다 어떤 시스템에서 더 지배적인지는 이론적인 관점에서 여전히 불분명하다.현재의 이론은 인장 표면 응력, 아돌마에 대한 표면 이완, 그리고 관련된 두 원자가 프로세스 전체에 걸쳐 높은 수준의 조정을 유지한다는 사실 때문에 중간의 안정성 증가 등 여러 가능성을 가리킨다.^[14][15]
• 터널링 확산은 입자가 확산 장벽을 통과하는 양자 터널링 효과의 물리적 표현이다.이는 낮은 확산 입자 질량과 낮은_diff E의 경우에 발생할 수 있으며, 텅스텐과 구리 표면에서 수소 확산의 경우에 관찰되었다.^[16]터널링 메커니즘이 지배하는 정권에서 확산률이 거의 온도에 구애받지 않는다는 점에서 이 현상은 독특하다.^[17]
• 공실 확산은 높은 커버리지 수준에서 완전한 커버리지에 근접하는 표면 확산의 주요 방법으로 발생할 수 있다.이 과정은 "슬라이딩 퍼즐"에서 조각들이 미끄러지는 방식과 유사하다.전형적으로 높은 확산률과 낮은 공실 농도로 인해 공실확산을 직접 관측하기는 매우 어렵다.^[18]그림 5는 비록 지나치게 단순화되었지만 이 메커니즘의 기본 주제를 보여준다.

그림 6.표면 확산 점프 메커니즘.FCC(100) 평면과 같은 사각 격자에서 발생할 수 있는 다양한 점프 다이어그램.1) 다양한 길이의 점프를 하는 분홍색 원자 2-5; 6) 녹색 원자는 위치 7로 대각선 점프를 하고, 8) 회색 원자는 반발 점프를 한다(원자는 시작했던 장소에 도달한다).근거리 점프는 일반적으로 높은 온도에서 더 큰 빈도로 이루어진다.규모를 조정하지 마십시오.	그림 7. 1차원 확산 시 Δx adatom 변위에 대한 상대 확률 분포를 보여주는 그래프.파란색: 단일 점프만 해당, 분홍색: 더블 점프는 싱글:더블 점프 = 1. 데이터의 통계 분석은 확산 메커니즘에 관한 정보를 산출할 수 있다.
그림 8.채널 표면(예: FCC(110), 파란색 및 강조 표시된 녹색 원자)의 아돔(회색)을 포함하는 채널 간 확산.1) 초기 구성, 2) "덤벨" 중간 구성최종 변위는 3, 4, 5 또는 초기 구성으로의 복귀를 포함할 수 있다.규모를 조정하지 마십시오.	그림 9.사각 격자에서의 표면 확산을 위한 장거리 원자 교환 메커니즘.표면(1)에서 쉬고 있는 아달톰(핑크)은 이웃 원자를 교란시키는 격자(2)에 삽입하여 궁극적으로 원래의 기질 원자 중 하나가 아달톰(녹색)(3)으로 나타나게 한다.규모를 조정하지 마십시오.

1970년대 후반부터 수행된 실험적인 작업뿐만 아니라 최근의 이론적인 작업은 메커니즘뿐만 아니라 운동학적 측면에서도 놀랄 만큼 다양한 표면 확산 현상을 밝혀냈다.다음은 보다 주목할 만한 현상의 일부를 요약한 것이다.

• 긴 점프는 인접하지 않은 흡착지로의 아달톰 이동으로 구성된다.가장 근접한 점프와 같은 방향으로 더블, 트리플 및 더 긴 점프를 포함하거나 그림 6과 같이 완전히 다른 방향에 있을 수 있다.그것들은 이론에 의해 많은 다른 시스템에 존재할 것으로 예측되어 왔고, 실험에 의해 0.1T_m(녹는 온도)의 낮은 온도에서 일어나는 것으로 증명되었다.높은 온도에서 단일 점프에 대한 확산 과정을 지배하는 긴 점프를 나타내는 데이터도 있다. 가변 점프 길이의 현상은 시간에 따른 원자 변위의 서로 다른 특성 분포로 표현된다(그림 7 참조).^[19]
• 리바운드 점프는 실험과 시뮬레이션에 의해 특정 시스템에서 발생하는 것으로 나타났다.이 동작으로 인해 관련 아돔이 순변위되지 않기 때문에, 반발 점프를 위한 실험 증거는 원자 분포의 통계적 해석에서 나온다.리바운드 점프는 그림 6에 나타나 있다.그러나 리바운드 점프는 채널 표면(특히 텅스텐의 BCc(211) 면)에서 1D 확산의 경우 실험적으로만 나타나기 때문에 약간 오해의 소지가 있다.^[20]
• 채널 표면의 경우 교차 채널 확산이 발생할 수 있다.일반적으로 채널 내 확산은 이 프로세스의 확산을 위한 낮은 에너지 장벽으로 인해 지배적이다.특정한 경우, 교차 채널이 발생하는 것으로 나타났으며, 이는 그림 8과 유사한 방식으로 발생한다.중간 "덤벨" 위치는 다양한 최종 원자 및 표면 원자 변위를 초래할 수 있다.^[21]
• 장거리 원자 교환은 정상적인 원자 교환 메커니즘에서처럼 표면에 원자핵을 삽입하는 과정이다. 그러나 가장 가까운 원자 대신에 그것은 출현하는 초기 원자로부터 어느 정도 떨어진 원자다.그림 9에 나타난 이 과정은 분자역학 시뮬레이션에서만 관찰되었으며 아직 실험적으로 확인되지 않았다.이러한 장거리 원자 교환과 더불어 다양한 다른 이국적인 확산 메커니즘에도 불구하고, 직접 관측하기에는 현재 너무 높은 온도에서 실질적으로 기여할 것으로 예상된다.^[22]

군집확산

군집 확산은 조광기에서 수백 개의 원자를 포함하는 섬들에 이르는 크기의 원자 군집의 움직임을 포함한다.군집 이동은 개별 원자, 군집 부분 또는 전체 군집 이동에 의해 한 번에 발생할 수 있다.^[23]이 모든 과정은 클러스터 질량 중심의 변화를 수반한다.

• 개별 메커니즘은 한 번에 한 원자의 움직임을 수반하는 메커니즘이다.^[24]
  • 가장자리 확산은 가장자리 또는 구부러진 부위의 아다톰 이동 또는 결원을 포함한다.그림 10과 같이 이동 원자는 프로세스 내내 클러스터와 근접성을 유지한다.
  • 증발 응축은 성단에서 테라스까지 원자를 "증발"하여 성단의 질량 중심 변화를 이끄는 성단으로 테라스 아다톰의 "응축"을 동반하는 것을 포함한다.그림 10은 동일한 원자가 성단에서 증발하고 응축됨을 나타내는 것으로 나타나지만, 실제로는 2D 기체로부터 응축되는 다른 원자일 수 있다.
  • 도약대 확산은 가장자리 확산과 유사하지만, 확산 원자가 실제로 클러스터 위에서 움직인 후 시작 위치와 다른 위치에 안착한다.
  • 순차적 변위는 한 번에 한 원자의 움직임을 수반하는 과정을 말하며, 가장 가까운 부지를 자유롭게 이동시킨다.

(a) 탈구	(b) 글라이드
(c) 파충류	(d) 전단
그림 11.클러스터 확산을 위한 일치된 메커니즘.

• 일치된 메커니즘은 클러스터 또는 전체 클러스터의 어느 한 섹션의 이동을 동시에 포함하는 메커니즘이다.^[25]
  • 탈구 확산은 탈구 변위를 통해 군집의 인접 서브 유니트가 일렬로 이동할 때 발생한다.그림 11(a)에 나타난 바와 같이, 프로세스는 탈구의 핵화와 결합한 기준으로 본질적으로 순차적 변위인 것으로 시작한다.
  • 글라이드 확산은 전체 클러스터의 결합 운동을 의미한다(그림 11(b) 참조).
  • 파충류는 클러스터 서브유닛의 순차적 움직임을 수반하는 뱀과 같은 움직임(이름 강조)이다(그림 11(c) 참조).
  • 피복은 군집 내 원자의 하위 단위를 결합한 변위(그림 11(d) 참조)이다).
• 크기 의존성: 군집 확산 속도는 군집 크기에 대한 의존도가 높으며, 군집 크기가 클수록 일반적으로 더 느린 확산에 해당한다.그러나 이는 보편적인 추세가 아니며 일부 시스템에서는 확산 속도가 일부 큰 군집에서는 그들보다 작은 군집보다 더 빠르게 확산되는 주기적인 경향을 보인다는 것이 밝혀졌다.^[26]

표면확산 및 이질적인 촉매

표면 확산은 종종 촉매 표면에서 서로 "찾는" 반응물질의 능력에 의해 반응률이 결정되기 때문에 이기종 촉매에서 매우 중요한 개념이다.온도 흡착 분자가 증가하면 분자 조각, 원자 및 군집은 이동성이 훨씬 더 큰 경향이 있다(식 1 참조).그러나 온도가 증가하면 흡착의 수명은 흡착된 종들이 탈착의 장벽을 극복할 수 있을 만큼 충분히_B 커짐에 따라 감소한다(그림 2 참조).반응 열역학과는 별도로 확산율 증가와 흡착 수명의 감소 사이의 상호작용으로 인해, 어떤 경우에는 온도 상승이 반응의 전체 비율을 감소시킬 수 있다.

실험적인

표면 확산은 직접 및 간접 관측을 포함한 다양한 기법에 의해 연구될 수 있다.이 연구 분야에서 매우 유용하다고 입증된 두 가지 실험 기법은 현장 이온 현미경과 스캐닝 터널링 현미경이다.^[3]시간이 지남에 따라 원자나 군집의 변위를 시각화함으로써, 관련 종(기계적 및 비율 관련 정보)이 확산되는 방식에 관한 유용한 정보를 추출할 수 있다.원자성 척도로 표면확산을 연구하기 위해서는 유감스럽게도 현장-이온 현미경 실험에서 He나 Ne를 영상가스로 사용할 때와 같이, 엄격하게 깨끗한 표면과 초고진공(UHV) 조건이나 소량의 불활성 기체가 있는 곳에서 연구를 수행해야 한다.

참고 항목

• 표면공학
• 표면과학
• 허위확산

참조

인용 작품

• G. Antczak, G. Ehrlich.표면 과학 보고서 62(2007), 39-61. (검토)
• Oura, K.; V.G. Lifshits; A.A. Saranin; A.V. Zotov; M. Katayama (2003). Surface Science: An Introduction. Springer-Verlag Berlin Heidelberg. ISBN 3-540-00545-5.
• Shustorovich, E. (1991). Metal-Surface Reaction Energetics: Theory and Applications to Heterogeneous Catalysis, Chemisorption, and Surface Diffusion. VCH Publishers, Inc. ISBN 3-527-27938-5.