페르마 포인트

기하학에서, 토리첼리 포인트 또는 페르마-라고도 불리는 삼각형의 페르마 포인트토리첼리 점(Torricelli point)은 삼각형의 세 꼭지점으로부터 점까지의 세 거리의 합이 가능한 가장 작은 점이다.^[1] 이 문제가 풀린 에반젤리스타 토리첼리에게 보낸 사서에서 페르마트가 처음 제기했기 때문에 그렇게 이름이 붙여진 것이다.

페르마 포인트는 기하학적 중위수와 스타이너 트리 문제에 대한 해결책을 세 점에 제공한다.

건설

최대 120°에서 가장 큰 각도를 가진 삼각형의 페르마 점은 단순히 최초의 이소곤 중심 또는 X(13)로서 다음과 같이 구성된다.

1. 주어진 삼각형의 임의로 선택한 두 변 각각에 정삼각형을 생성한다.
2. 각 새 꼭지점에서 원래 삼각형의 반대 정점까지 선을 그린다.
3. 두 선은 페르마 지점에서 교차한다.

다른 방법은 다음과 같다.

1. 임의로 선택한 두 변에 각각 이등변 삼각형을 구성하되, 이등변 삼각형을 원삼각형 바깥에 놓여 있는 각 이등변 삼각형의 세 번째 꼭지점인 30도 각 이등변 삼각형은 원삼각형 바깥쪽에 위치한다.
2. 각 이등변 삼각형에 대해, 각 경우에서 이등변 삼각형의 새로운 꼭지점에 중심을 두고 이등변 삼각형의 새로운 두 변과 반지름을 각각 같게 하여 원을 그린다.
3. 두 원 사이의 원래 삼각형 안에 있는 교차점은 페르마 지점이다.

삼각형의 각도가 120°보다 크면, 페르마트 지점은 둔각 정점에 위치한다.

"사례 1" 다음에 나오는 것은 삼각형의 각도가 120°를 초과한다는 것을 의미한다. "사례 2"는 삼각형의 각도가 120°를 초과하지 않음을 의미한다.

X(13)의 위치

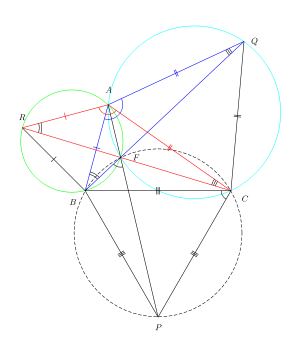
그림 2는 임의 삼각형 ABC의 횡방향에 부착된 정삼각형 ARB, AQC 및 CPB를 나타낸다. 그림 2의 세 선 RC, BQ 및 AP가 모두 F 지점에서 교차하고 60° 각도에서 서로를 절단한다는 것을 보여주기 위해 순환 점의 특성을 사용하는 증거가 여기에 있다.

두 번째가 첫 번째 A에 대한 60° 회전이기 때문에 삼각형 RAC와 BAQ는 일치한다. 따라서 ∠ARF = ∠ABF 및 ∠AQF = ∠ACF. 세그먼트 AF에 적용된 새겨진 각도 정리의 역에 의해, ARBF 포인트는 순환(원 위에 놓여 있다)이다. 마찬가지로, AFCQ도 반복적이다.

∠ARB = 60°이므로 ∠AFB = 120°, 새겨진 각도 정리를 사용한다. 마찬가지로 ,AFC = 120°

따라서 ∠BFC = 120° 따라서 ∠BFC와 ∠BPC는 최대 180°에 이른다. 이것은 새겨진 각도 정리를 이용하여 BPCF 점들이 순환임을 암시한다. 따라서 세그먼트 BP에 적용된 새겨진 각도 정리를 이용하여 usingBFP = ∠BCP = 60° ∠BFP + ∠BFA = 180°이기 때문에 F 지점은 선 세그먼트 AP에 있다. 따라서 RC, BQ 및 AP 선은 동시(단일 지점에서 교차)이다. Q.E.D.

이 증거는 proofBAC > 120°인 경우 A 지점이 A와 F의 상대적 위치를 전환하는 BPC의 원곡선 안에 있기 때문에 케이스 2에만 적용된다. 그러나 사례 1을 다루도록 쉽게 수정된다. 그 다음 ∠AFB = afAFC = 60°이므로 ∠BFC = ∠AFB + ∠AFC = 120° 즉, BPCF는 순환하므로 ∠BFP = ∠BCP = 60° = ∠BFA. 따라서 A는 FP에 놓여 있다.

그림 2의 원 중심에 연결되는 선은 선 세그먼트 AP, BQ 및 CR에 수직이다. 예를 들어 ARB를 포함하는 원의 중심과 AQC를 포함하는 원의 중심을 연결하는 선은 세그먼트 AP에 수직이다. 그래서 원의 중심을 잇는 선들도 60° 각도로 교차한다. 따라서 원의 중심은 정삼각형을 이룬다. 이것은 나폴레옹의 정리라고 알려져 있다.

페르마 포인트의 위치

전통 기하학

유클리드 삼각형 ABC와 임의 지점 P가 있으면 d(P) = PA+PB+PC를 허용하고 PA는 P와 A 사이의 거리를 나타낸다. 이 조의 목적은 모든 P ≠ P에₀ 대해 d(P₀) < d(P)>와 같은 점 P를₀ 식별하는 것이다. 만약 그러한 점이 존재한다면 그것은 페르마트 점일 것이다. Δ는 삼각형 내부의 점을 나타내며 경계 Ω을 포함하도록 취해진다.

중요한 결과는 삼각형과 다각형이 한 면을 공통으로 가지고 있고 나머지 삼각형이 다각형 안에 있으면 삼각형이 다각형보다 더 짧은 둘레를 갖는다고 주장하는 독단법칙이다.
[AB가 공통면인 경우 AC를 연장하여 폴리곤을 X에서 절단한다. 그런 다음 삼각형 부등식으로 다각형 둘레 > AB + AX + XB = AB + AC + CX + XB ≥ AB + AC + BC.]

P를 Δ 밖의 어떤 점으로 두십시오. 각 정점을 원격 영역, 즉 반대쪽(확장)을 넘는 반평면과 연결하십시오. 이 3개 구역은 Δ 자체를 제외한 전체 평면을 포함하며, P는 그 중 하나 또는 두 개에 분명히 놓여 있다. P가 두 개(B와 C 구역 교차점이라고 함) 안에 있는 경우, D' = A를 설정하면 D(P') = d(A) < d(P)를 의미한다. 또는 P가 하나의 영역에만 있는 경우, A-Zone, d(P) < 여기서 P'는 AP와 BC의 교차점이라고 한다. 따라서 Δ를 제외한 모든 포인트 P에 대해 Ω에 d(P') < d(P)와 같은 포인트 P'가 존재한다.

사례 1. 삼각형의 각도는 120°이다.

일반성을 상실하지 않고 A의 각도가 120°라고 가정한다. 등변 삼각형 AFB를 구성하고 Δ(A 자체를 제외한)의 임의의 점 P에 대해 Q를 구성하여 삼각형 AQP가 등변형이고 표시된 방향을 갖도록 한다. 그러면 삼각형 ABP는 A에 대한 삼각형 AFQ의 60° 회전이기 때문에 이 두 삼각형은 합치되며 d(P) = CP+PQ+QF 경로의 길이인 것을 따른다. P는 ABC 내에 있어야 하므로, Dogleg 규칙에 의해 이 경로의 길이가 AC+를 초과한다.AF = d(A) 따라서 모든 P Δ, P ( A에 대해 d(A) < d(P). 이제 P가 Δ를 벗어나도록 허용한다. 점 P' є Ω은 d(P) < d(P)>와 같이 위로부터 존재하며, d(A) ≤ d(P')로서 Δ를 제외한 모든 P에 대해 d(A) < d(P)를 따른다. 따라서 모든 P ≠ A에 대해 d(A) < d(P)는 A가 Δ의 페르마 지점임을 의미한다. 즉, 페르마 지점은 둔각으로 된 정점에 놓여 있다.

사례 2. 삼각형의 각도는 120°가 없다.

등변 삼각형 BCD를 구성하고 P를 Δ 내부의 어떤 점으로 하고 등변 삼각형 CPQ를 구성한다. CQD는 C에 대한 CPB의 60° 회전이기 때문에 d(P) = PA+PB+PC = AP+PQ+QD 경로의 길이일 뿐이다. P는₀ AD와 CF가 교차하는 지점이다. 이 점을 흔히 제1 이소곤 중심이라고 부른다. P와 같은 운동을 P와₀ 함께 하고, 포인트 Q를₀ 찾아라. 각도 제한 P에₀ 의해 Δ 안에 위치하며 BCF는 B에 대한 BDA의 60° 회전이기 때문에 Q는₀ AD 어딘가에 위치해야 한다. CDB = 60°이므로 Q가₀ P와₀ D 사이에 있으므로 APQD는₀₀ 직선이기 때문에 d(P₀) = AD를 의미한다. 더욱이 P ≠ P가₀ 되면 P나 Q가 d(P₀) = AD < d(P)를 의미하는 AD에 눕지 않게 된다. 이제 P가 Δ를 벗어나도록 허용한다. 점 P' є Ω은 d(P) > d(P) > d(P)와 같이 위로부터 존재하며, d(P₀) Δ를 제외한 모든 P에 대해 d(P₀) < d(P)를 따른다. 즉, P는₀ 페르마 지점인 Δ를 의미한다. 즉 페르마트 지점은 첫 번째 이소곤 중심과 일치한다.

벡터 분석

O, A, B, C, X를 평면에서 다섯 점으로 한다. Denote the vectors ${\displaystyle {\overrightarrow {\mathrm {OA} }},{\overrightarrow {\mathrm {OB} }},{\overrightarrow {\mathrm {OC} }},{\overrightarrow {\mathrm {OX} }}}$ by a, b, c, x respectively, and let i, j, k be the unit vectors from O along a, b, c.
이제 a = a⋅i = (a - x)⋅i + x⋅i ≤ a - x + x⋅i 그리고 마찬가지로 b ≤ b - x + x⋅j와 c ≤ c - x x⋅k.
추가하면 + b + c ≤ a - x + b - x + c - x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x ⋅(i + j + k)
a, b, c가 120° 각도에서 O에서 만나는 경우, 모든 x에 대해 i + j + k = 0이므로 a + b + c + c ≤ a - x + b - x - x - x
즉 OA + OB + OC ≤ XA + XB + XC이며 따라서 O는 ABC의 페르마트 지점이다.
이 주장은 a, b, c가 120°의 각도에서 만나는 지점 O가 없기 때문에 삼각형이 angleC > 120°의 각도를 가질 때 실패한다. 그럼에도 불구하고, k = - (i + j)를 재정립하고 O를 C에 배치하여 c = 0으로 하면 쉽게 고정된다. 단위의 벡터 i와 j 사이의 각도가 120°를 초과하는 ∠C이기 때문에 k ≤ 1에 유의한다. 0 ≤ 0 - x + x kk 세 번째 불평등이 여전히 유지되고 있기 때문에, 나머지 두 가지 불평등은 변하지 않는다. 이제 증거는 위와 같이 계속된다(이 경우 O(또는 C)가 ABC의 페르마트 지점이어야 한다는 동일한 결론에 도달하기 위해 i + j + k = 0을 사용한다).

라그랑주 승수

삼각형의 정점까지의 거리의 합이 최소인 삼각형 안에서 점을 찾는 또 다른 접근법은 수학 최적화 방법 중 하나를 사용하는 것인데, 특히 라그랑주 승수의 방법과 코사인의 법칙을 이용하는 것이다.

우리는 삼각형의 점으로부터 그 정점까지 선을 그리고 X, Y, Z라고 부른다. 또한 이러한 선의 길이는 각각 x, y, z가 되도록 한다. X와 Y 사이의 각도는 α, Y와 Z는 β가 되도록 한다. 그러면 X와 Z 사이의 각도는 (2㎛ - α - β)이다. 라그랑주 승수의 방법을 사용하여 우리는 다음과 같이 표현되는 라그랑주 L의 최소치를 찾아야 한다.

L = x + y + z + λ₁ (x² + y - 2xy² cos(α) - a²) + λ₂ (y² + z - 2yz² cos(β) - b²) + λ₃ (z²² + 2zx cos(α + β) - c²)

여기서 a, b, c는 삼각형의 변의 길이다.

5개의 부분파생상품 ΔL/Δx, ΔL/Δz, ΔL/Δα, ΔL/Δβ를 각각 0에 동일시하고 Δ, Δ₁, Δ₂₃, sin(α + β)을 제거하면 결국 sin(α) = sin(β) = - sin(β) = 120° 그러나 제거는 길고 지루한 사업이며 최종 결과는 사례 2에 불과하다.

특성.

• 삼각형의 가장 큰 각도가 120°보다 크지 않을 때, X(13)는 페르마 지점이다.
• X(13)에서 삼각형의 횡방향으로 하위 각도를 이루는 각도는 모두 120°(사례 2) 또는 60°, 60°, 120°(사례 1)와 같다.
• 구성된 3개의 정삼각형의 원주는 X(13)에서 동시에 이루어진다.
• 첫 번째 등심 중심 X(13)에 대한 삼선 좌표:

csc(A + π/3) : csc(B + π/3) : csc(C + π/3) 또는 동등하게

초(A - π/6) : 초(B - π/6) : 초(^[2]C - π/6)

• 두 번째 등심 중심 X(14)에 대한 삼선 좌표:

csc(A - π/3) : csc(B - π/3) : csc(C - π/3) 또는 동등하게

초(A + π/6) : 초(B + π/6) : 초(^[3]C + π/6)

• 페르마 지점에 대한 트리린 좌표:

1 - u + ubw 초(A - π/6) : 1 - v + ubw 초(B - π/6) : 1 - w + ubw 초(C - π/6)

여기서 u, v, w는 각각 부울 변수(A<120°), (B<120°), (C<120°)를 나타낸다.

• X(13)의 등각 결합은 첫 번째 등역학적 점, X(15)이다.

sin(A + π/3) : sin(B + π/3) : sin(^[4]C + π/3)

• X(14)의 등각 결합은 두 번째 등역학적 점, X(16)이다.

sin(A - π/3) : sin(B - π/3) : sin(^[5]C - π/3)

• 다음 삼각형은 등각형이다.

X(13)의 대척 삼각형

X(14)의 대척 삼각형

페달 삼각형 X(15)

페달 삼각형 X(16)

X(15)의 원주 삼각형

X(16)의 원주 삼각형

• X(13)X(15)와 X(14)X(16)는 오일러 선과 평행하다. 세 선은 오일러 무한점 X(30)에서 만난다.
• X(13) X(14) X(14), 원곡선 및 9점 중심은 레스터 원에 놓여 있다.
• X(13)X(14) 라인은 X(2)와 X(4)의 중간 지점에서 오일러 라인과 만난다.^[6]
• 페르마트 지점은 자신의 중심에 구멍이 난 열린 직교성 항진 원반 안에 있으며, 그 안에 어떤 지점이 될 수도 있다.^[7]

별칭

이소곤 중심 X(13)와 X(14)는 각각 첫 번째 페르마트 지점과 두 번째 페르마트 지점으로도 알려져 있다. 대안으로는 포지티브 페르마트 포인트와 네거티브 페르마트 포인트가 있다. 그러나 이러한 다른 이름들은 혼동될 수 있고 아마도 가장 잘 피할 수 있을 것이다. 문제는 문헌의 많은 부분이 페르마 포인트와 최초의 페르마 포인트의 구분을 흐리게 하는 데 반해, 위의 사례 2에서만 그것들이 실제로 같다는 것이다.

역사

이 질문은 에반젤리스타 토리첼리에게 도전하기 위해 페르마트가 제안한 것이다. 그는 대신 세 개의 정삼각형의 원곡선 교차점을 사용하기는 했지만 페르마의 원곡선과 비슷한 방법으로 문제를 해결했다. 그의 제자인 비비아니는 1659년에 해결책을 발표했다.^[8]

참고 항목

• 기하학적 중위수 또는 Fermat-Weber 점, 주어진 점 3개 이상으로 거리의 합을 최소화하는 점.
• 레스터 정리
• 삼각 중심
• 나폴레옹은 지적한다.
• 베버 문제

참조

외부 링크

• "Fermat-Torricelli problem", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Wolfram 데모 프로젝트인 Chris Boucher의 Fermat Point.
• 동적 지오메트리 스케치의 페르마트-토리첼리 일반화 대화형 스케치는 페르마트-토리첼리 포인트를 일반화한다.
• 페르마 포인트의 실제 사례
• iOS 대화형 스케치