자유 에너지 원리

자유 에너지 원리는 제한된 수의 주(州)로 제한함으로써 어떻게 생활 및 비생활 시스템이 비균형 안정 상태에 머물러 있는지를 설명하는 공식 성명이다.그것은 시스템이 (열역학적 자유 에너지와 혼동되지 않도록) 내부 상태의 자유 에너지 기능을 최소화한다는 것을 확립하며, 이는 환경에 숨겨진 상태에 대한 믿음을 수반한다.자유 에너지의 암묵적 최소화는 공식적으로 다양한 베이지안 방법과 관련이 있으며, 원래 칼 프리스톤에 의해 신경과학에 내재된 지각에 대한 설명으로 도입되었는데,^[1] 여기서도 능동적 추론이라고 알려져 있다.

자유 에너지 원리는 주어진 시스템의 존재를 마르코프 담요를 통해 모형화하여 그들의 세계 모델과 감각과 관련 인식의 차이를 최소화하려고 노력한다.이러한 차이는 "깜짝 놀랄 만한" 것으로 설명할 수 있으며, 시스템의 세계 모델을 지속적으로 수정함으로써 최소화된다.이와 같이 이 원리는 '추론 엔진'으로서 뇌에 대한 베이시안 사상에 근거하고 있다.프리스톤은 최소화를 위해 두 번째 루트를 추가했다.세계를 예상된 상태로 능동적으로 변화시킴으로써, 시스템은 또한 시스템의 자유 에너지를 최소화할 수 있다.프리스톤은 이것을 모든 생물학적 반응의 원리로 가정한다.^[2]프리스톤은 또한 그의 원칙이 인공지능뿐만 아니라 정신 장애에도 적용된다고 믿는다.능동적 추론 원리에 기초한 AI 구현은 다른 방법보다 장점을 보였다.^[2]

자유 에너지 원리는 전문가들조차^[3] 이해하기 매우 어렵다는 비판을 받아왔으며, 이론의 수학적 일관성도 최근 연구에 의해 의심받고 있다.^[4][5]그 원리에 대한 논의는 또한 시험 가능한 과학적 예측과는 거리가 먼 형이상학적 가정을 불러일으켜 그 원리가 타당하지 못하게 만든다는 비판을 받아왔다.^[6]2018년 인터뷰에서, 프리스톤은 자유 에너지 원칙이 제대로 위조될 수 없다는 것을 인정했다: "자유 에너지 원칙이 바로 그것이다 - 원칙이다.해밀턴의 정지 동작 원리처럼 위변조가 불가능하다.그것은 반증할 수 없다.사실 측정 가능한 시스템이 원리에 부합하는지를 묻지 않는 한 그것을 가지고 할 수 있는 일은 많지 않다."^[7]

배경

세포나 뇌와 같이 스스로 조직되는 생물학적 시스템이 변동 가능한 자유 에너지를 최소화하는 것으로 이해될 수 있다는 개념은 심리학과^[9] 기계학습에서 무의식적인 추론과^[8] 그에 따른 치료에 대한 헬름홀츠의 연구에 바탕을 두고 있다.^[10]변동 자유 에너지는 관측치의 함수와 그 숨겨진 원인에 대한 확률 밀도다.이 변동 밀도는 귀무 가설의 원인으로부터 예측 관측치를 생성하는 확률론적 모델과 관련하여 정의된다.이 설정에서 자유 에너지는 베이지안 모델 증거에 근사치를 제공한다.^[11]따라서, 그것의 최소화는 베이시안 추론 과정으로 볼 수 있다.시스템이 자유 에너지를 최소화하기 위해 능동적으로 관찰할 때, 그것은 암묵적으로 능동 추론을 수행하고 그것의 세계 모델에 대한 증거를 최대화한다.

그러나, 자유 에너지는 또한 결과의 자기 정보에 대한 상한이며, 여기서 놀라움의 장기 평균은 엔트로피이다.즉, 시스템이 자유 에너지를 최소화하기 위해 작용하는 경우 시스템이 샘플링하는 결과의 엔트로피(또는 감각 상태)에 대해 암묵적으로 상한을 부여할 것이다.^{[12][13][better source needed]}

다른 이론과의 관계

능동적 추론은 자기조립, 패턴 형성, 자기조립^[17], 자기조립, 연습과 ^[15][16]같은 자기조직의 좋은 조절기 정리^[14] 및 관련 설명과 밀접하게 관련되어 있다.^[18]그것은 사이버네틱스, 시너지틱스^[19], 구현된 인식에서 고려된 주제를 다룬다.자유 에너지는 변동 밀도에서 엔트로피를 뺀 관측치의 예상 에너지로 표현할 수 있기 때문에 최대 엔트로피 원리와도 관련이 있다.^[20]마지막으로 에너지의 시간 평균은 작용이기 때문에 최소변동 자유 에너지의 원리는 최소 작용의 원리다.

정의

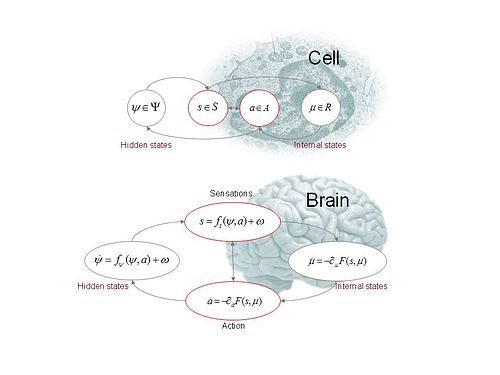
정의(연속 공식):활성 추론은 튜플$({\displaystyle \mathrm{\Omega }}$, ${\displaystyle \psi }$, ${\displaystyle S}$, A${\displaystyle }$, R ,${\displaystyle q}$, ${\displaystyle p}$) ${\displaystyle(\Oomega ,\PSI ,S,A,R,q,p)}$에 있다.

• $\Omega {\displaystyle \mathrm{}}$ ${\displaystyle \Oomega}$ – 임의 $$변동 $\Omega {\displaystyle \mathrm{\Omega }}$ ${\displaystyle \omega$\in$}$이(가) 그려지는$$ 샘플 공간
• 숨겨진 상태 또는 외부 상태 $\psi {\displaystyle \mathrm{}}$ :${\displaystyle \psi }$ ${\displaystyle \times }$ A${\displaystyle \mathrm{\Omega }}$→ ${\displaystyle R\mathbb{}}$ ${\$time A$\Oomega \to \mathb {R}}$ – 감각 상태를 유발하고 동작에 의존함
• 감각 ${\displaystyle \mathrm{상태}}$ $S{\displaystyle }$: × ${\displaystyle \times }$ ${\displaystyle A\Omega \mathbb{}}$→ R ${\$ S$:\Psi \time$A\times $\Oomega$ \$to \mathb {R}$ $$– 동작 및 숨겨진 상태의 확률적 매핑
• 조치 $A{\displaystyle }$: ${\displaystyle S}$ ${\displaystyle \times }$ R${\displaystyle }$→ ${\displaystyle R\mathbb{}}$ ${\$$S\time R\to \mathb {R}$– 감각 및 내부 상태에 따라 다름
• ${\displaystyle 내부\mathbb{}}$ 상태 $R{\displaystyle }$: ${\displaystyle R}$ ${\displaystyle \times }$ S${\displaystyle }$→ R ${\$ 스타일 $R:$$동작$을 유발하고 감각 상태에 따라$달라지는$ R\time S$\to$ $$$\mathb$ {R}$}$
• 생성 $밀도{\displaystyle }$ p${\displaystyle (s}$ ,${\displaystyle \psi }$ ${\displaystyle \mid }$ m${\displaystyle }$) ${\displaystyle p(s,\psi \mid m)}$ $$– 생성 모델 m ${\displaystyle m}$ 아래의 감각 및 숨겨진 상태
• 가변 밀도 $q{\displaystyle (\psi \mu }$) ${\displaystyle q(\psi \mid$\mid \$mu )}$ $$– 내부 $상태{\displaystyle }$ ${\displaystyle \mu }$에 의해 매개 변수화된 숨겨진$$ 상태 ${\displaystyle \mathrm{\psi }}$ ${\displaystyle \in }$ ∈ ∈ ∈ { { ${$${\displaystyle }$$\$ \$psi$$$\$in \psi$$}}.$

행동과 인식

목적은 모델 증거 $p{\displaystyle (s}$ ${\displaystyle \mid m}$) ${\displaystyle p(s\mid$ m$)}$을(를) 최대화하거나$$ 깜짝 -${\displaystyle \log }$ ${\displaystyle p(s}$ ${\displaystyle \mid }$ $){\displaystyle$ -$\log p(s\mid$ m$)}$ 최소화하는 것이다$.$이것은 일반적으로 숨겨진 상태에 대한 난치할 수 없는 한계화를 수반하므로, 놀라움은 상단의 변동 자유 에너지 바인딩으로 대체된다.^[10]그러나 이는 자유 에너지는 감각 및 내부 상태의 기능이기 때문에 내부 상태도 자유 에너지를 최소화해야 함을 의미한다.

${\displaystyle a(t)={\underset {a}{\operatorname {arg\,min}}}}}}{F(s(t),\mu(t)\}}$

${\displaystyle \mu (t)={\underset {\mu }{\operatorname {arg\,min}}}}}}}}}{F(s(t),\mu )\}}}}}}$

${\displaystyle {\underset {\mathrm {free-energy} }{\underbrace {F(s,\mu )} }}={\underset {\mathrm {energy} }{\underbrace {E_{q}[-\log p(s,\psi \mid m)]} }}-{\underset {\mathrm {entropy} }{\underbrace {H[q(\psi \mid \mu )]} }}={\underset {\mathrm {surprise} }{\underbrace {-\log p(s\mid m)} }}+{\underset {\mathrm {divergence} }{\underbrace {D_{\mathrm {KL} }[q(\psi \mid \mid \mu )\병렬 p(\psi \mid s,m)]}}}}}}}}}}}}}}}}}}}\geq {\dmatherset {\mathrm {surprise}{\brace-\log p(s\mid m)}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$

이것은 각각 행동과 인식에 해당하는 내부 상태와 관련하여 이중 최소화를 유도한다.

자유 에너지 최소화

자유 에너지 최소화 및 자체 조직

자유 에너지 최소화는 무작위 동적 시스템으로 주조될 때 자체 구성 시스템의 특징으로 제안되었다.^[21]이 공식은 내부와 외부 상태를 구분하는 마르코프 담요(복합 작용 및 감각 상태)에 위치한다.내부 상태와 작용이 자유 에너지를 최소화하는 경우, 그들은 감각 상태의 엔트로피에 상한을 둔다.

${\displaystyle \lim _{T\to \inflat }{\frac {1}{T}{{\underset{\text-action}{\ndbrace{\nt_{0}^{0}F(s(t),\mu(t)\,dt}}}}}}}}\geq \lim \to \flot }{\frac {1}{\1}{\}}}}}{T}}\int _{0}^{T}{{\underset{\텍스트{surprise}{\\underbrace {-\log p(t)\mid m)}}}}}}},dt=H[p(s\mid m)]}$

왜냐하면 - 에르고딕적 가정 하에서, 놀라움의 장기 평균은 엔트로피이기 때문이다.이러한 결합은 열역학 제2법칙과 변동 정리 등과 관련된 종류의 자연적인 무질서의 경향에 저항한다.그러나 무작위 역학 시스템, 비균형 안정 상태 및 인간성과 같은 통계 물리학으로부터의 개념의 관점에서 생명 과학에 대한 통일 원리를 형성하는 것은 생물학적 시스템을 만드는 모든 특징을 가릴 위험으로 생물 시스템의 이론적 및 경험적 연구에 상당한 제약을 가한다.재미있는 종류의 자기 만족 시스템^[22]

자유 에너지 최소화와 베이지안 추론

모든 베이시안 추론은 자유 에너지 최소화^{[23][failed verification]} 측면에서 제시될 수 있다.내부 상태에 대해 자유 에너지가 최소화된 경우, Kullback-Leibler는 숨겨진 상태에 대한 가변적 밀도와 후방 밀도 사이의 차이를 최소화한다.이는 변동 밀도의 형태가 고정되어 있을 때 대략적인 베이지안 추론에 해당하며, 그렇지 않을 경우 정확한 베이지안 추론에 해당한다.따라서 자유 에너지 최소화는 베이시안 추론 및 필터링(예: Kalman 필터링)에 대한 일반적인 설명을 제공한다.또한 베이지안 모델 선택에도 사용되며, 여기서 자유 에너지는 복잡성과 정확성으로 유용하게 분해될 수 있다.

${\displaystyle {\underset {\text{free-energy}}{\underbrace {F(s,\mu )} }}={\underset {\text{complexity}}{\underbrace {D_{\mathrm {KL} }[q(\psi \mid \mu )\parallel p(\psi \mid m)]} }}-{\underset {\mathrm {accuracy} }{\underbrace {E_{q}[\log p(s\mid \psi ,m)]} }}}$

최소 자유 에너지를 가진 모델은 복잡성 비용(Cocam의 면도기 및 더 공식적인 계산 비용^[24] 처리)에서 데이터에 대한 정확한 설명을 제공한다.여기서 복잡성은 숨겨진 상태에 대한 가변적 밀도와 이전 믿음 사이의 차이(즉, 데이터를 설명하는 데 사용되는 유효 자유도)이다.

자유 에너지 최소화 및 열역학

가변 자유 에너지는 정보-이론적 기능이며 열역학(Helmholtz) 자유 에너지와 구별된다.^[25]그러나 가변 자유 에너지의 복잡성 용어는 헬름홀츠 자유 에너지와 동일한 고정 지점을 공유한다(시스템이 열역학적으로 폐쇄되지만 격리되지는 않는다는 가정 하에).이는 감각 동요가 (적정히 긴 시간 동안) 중단되면 복잡성이 최소화되기 때문이다(정확성이 무시될 수 있기 때문이다).이 시점에서, 시스템은 평형 상태에 있고 내부 상태는 최소 에너지의 원리에 의해 헬름홀츠 자유 에너지를 최소화한다.^[26]

자유 에너지 최소화 및 정보 이론

자유 에너지 최소화는 (고정 엔트로피 변동 밀도의 경우) 변이 밀도를 매개하는 감각 상태와 내부 상태 사이의 상호 정보를 최대화하는 것과 동등하다.^{[12][better source needed]}이것은 자유 에너지 최소화와 최적의 행동을 기술하기 위한 정보이론을 이용한 최소 중복성^[27] 및 관련 치료의 원리와 관련된다.^[28][29]

신경 과학에서 자유 에너지 최소화

자유 에너지 최소화는 불확실성^[30] 하에서 뉴런 추론과 학습의 규범적(베이지스 최적) 모델을 공식화할 수 있는 유용한 방법을 제공하므로 베이시안 뇌 가설을 구독한다.^[31]자유 에너지 최소화에 의해 설명되는 뉴런 ${\displaystyle \mathrm{프로세스}}$는 숨겨진 상태의 특성에 따라 달라진다: :${\displaystyle }$= X ${\displaystyle \times }$ × ${\displaystyle \times }$ ${\displaystyle \mathrm{\pi }}$ {$$\$displaystyle \\PSI$ = $X\times \time$ \time \$Pi$ \time $\time$ \timensions \time$$$$\pi \time \time \piecondition 또는 \pi \pi \pi.변수, 매개변수, 정밀도를 최소화하는 것은 각각 추론, 학습, 불확실성의 인코딩에 해당한다.

지각적 추론과 분류

자유 에너지 최소화는 지각에서^[8][10] 무의식적인 추론 개념을 공식화하고 뉴런 처리의 규범적(베이지안) 이론을 제공한다.뉴런 역학의 관련 프로세스 이론은 구배 강하를 통한 자유 에너지 최소화에 기초한다.이는 일반화된 베이지안 필터링에 해당된다(여기서 ~는 동작의 일반화된 좌표에서 변수를 나타내며 D ${\displaystyle D}$은(는) 파생 매트릭스 연산자임).^[32]

${\dot스타일 {\dote {\tilde {\mu }}=D{\tilde {\mu }-\partial _{\mu }F(s,\mu ){\Big }_{\mu ={\tilde {\mu }}}}}}}}}}}}}}}}}}}}}.$

보통 자유 에너지를 정의하는 생성 모델은 비선형적이고 계층적(뇌 속의 피질적 위계처럼)이다.일반화된 필터링의 특별한 경우로는 Kalman 필터링이 있는데, Kalman 필터링은 뇌의 메시지 전달에 대한 일반적인 은유인 예측^[33] 코딩에 해당한다.계층적 모델에서 예측 코딩은 감각^[35] 및 운동 시스템의 해부학 및 생리학과 일치하는 상승(하강) 예측 오류와 하강(하강) 예측의^[34] 반복적인 교환을 포함한다.^[36]

지각학습과 기억력

예측 코딩에서 자유 에너지의 시간 적분(자유 작용)에 대한 구배 강하를 통해 모델 매개변수를 최적화하면 연관성 또는 헤비안 가소성으로 감소하고 뇌의 시냅스 가소성과 관련이 있다.

지각 정밀도, 주의력, 주의력

정밀도 파라미터를 최적화하는 것은 예측오차의 이득(c.f, Kalman gain)을 최적화하는 것과 일치한다.예측 코딩의 뉴런적으로 타당한 구현에서,^[34] 이것은 피상적인 피라미드 세포의 흥분성을 최적화하는 것과 일치하며 주의력 획득의 관점에서 해석되었다.^[37]

주요 공개 관심사로 다뤄진 하향식 대 상향식 논쟁에 대해, 연산 모델은 하향식 메커니즘과 상향식 메커니즘 사이의 상호주의의 순환적 성격을 설명하는 데 성공했다.저자들은 확립된 비상식 관심 모델, 즉 SAIM을 사용하여, 표준 버전과 대조적으로 하향식 관심에서 선택적 관심에 접근하는 PE-SAIM이라는 모델을 제안했다.모델은 데이터와 그 원인의 차이를 나타내는 에너지 함수 또는 즉, 생성 모델과 후방의 차이를 최소화하기 위해 동일한 수준 또는 위의 수준으로 전송되는 포워딩 예측 오류를 고려한다.유효성을 높이기 위해, 그들은 또한 모형의 자극들 사이의 신경 경쟁을 통합했다.이 모델에서 주목할 만한 특징은 작업 수행 중 예측 오류 측면에서만 자유 에너지 함수를 재조정한다는 점이다.

${\dfrac {\dfrac {\partial E^{total}(Y^{VP},X^{SN},x^{})CN},y^{KN}}{\partial y_{mn}^{{n}}}SN}}}=x_{mn}^{CN}-b^{CN}\varepsilon _{nm}^{CN}+b^{CN}\sum _{k}(\varepsilon _{knm}^{KN})}$

여기서 $E{\displaystyle {}^{}}$ ${\displaystyle t^{}}$ ${\displaystyle o^{}}$ a ${\$ E$^{total}}$는 신경망을 수반하는 총 에너지 함수이며, ${\displaystyle {\mathrm{andknm}}_{}^{}}$ K ${\displaystyle N_{}^{}}$ ${\$은 생성$$ 모델(사전)과 후향 변화 사이의 예측 오차이다.^[38]두 모델을 비교하면 각각의 결과 사이에 현저한 유사성이 나타나며 SAIM의 표준 버전에서는 모델이 주로 호기성 연결에 초점을 맞추는 반면 PE-SAIM에서는 억제 연결을 활용하여 추론을 한다.이 모델은 또한 인간 실험에서 도출된 EEG와 fMRI 데이터를 고도로 정밀하게 예측하는 데 적합하다는 것이 증명되었다.같은 맥락에서 야히아 외 연구진은 자유 에너지 원리를 적용하여 주로 SAIM에 의존하는 은밀한 선택적 시각 주의에서 템플릿 매칭에 대한 연산 모델을 제안하였다.본 연구에 ^[39]따르면, 원래의 신경망에 하향식 신호를 삽입하여 전체 상태 공간의 총 자유 에너지에 도달하고, 여기서 피드-포워드 및 후진 예측 오차를 모두 포함하는 동적 시스템을 도출한다.

적극추론

${\displaystyle \stackrel{}{\dot{}}}$= -${\displaystyle {\mathrm{}}_{}}$ a ${\displaystyle {}_{}(s}$ ,${\displaystyle \mu \stackrel{}{}}$~$){\dot{a}=-\partial _{a}F(s,{\tilde{\mu$ $\}\}\}\}\}\}\}\}$ $동작$에 구배 강하를 적용하면 내림(구경) 예측에 의해 관여하는 고전적인 반사 호 측면에서 모터 제어를 이해할 수 있다.이것은 평형점 해결책(자유도 문제^[40] 정도)을 이동 궤도에 일반화하는 형식주의를 제공한다.

능동적 추론 및 최적 제어

능동적 추론은 상태 전환이나 흐름에 대한 이전의 믿음으로 가치나 비용 대비 기능을 대체함으로써 최적의 제어와 관련이 있다.^[41]이것은 베이지안 필터링과 벨만 방정식의 해법 사이의 밀접한 관계를 이용한다.However, active inference starts with (priors over) flow ${\displaystyle f=\Gamma \cdot \nabla V+\nabla \times W}$ that are specified with scalar ${\displaystyle V(x)}$ and vector ${\displaystyle W(x)}$ value functions of state space (c.f., the Helmholtz decomposition).여기서 $\gamma {\displaystyle \mathrm{}}$ ${\displaystyle \Gamma}$은 랜덤 변동의 진폭이며 비용은 ${\displaystyle c}$( x${\displaystyle }$)${\displaystyle }$= ${\displaystyle f}$ ${\displaystyle \mathrm{\cdot }}$ V${\displaystyle }$+ ${\displaystyle \nabla }$ ⋅ ⋅ ⋅ ⋅ ${\displaystyle \cdot }$ ${\displaystyle V}$ {\$displaystyle c(x)=f\cdot \nabla V+\cdot$\감마 $\cdot$ V$}$이다$.$flow $p{\displaystyle }$( ${\displaystyle x\stackrel{}{}}$~ $){\displaystyle p({\tilde{x}}\mid$ $m$$)}$은(는) 적절한 전방 Kolmogov 방정식에 대한 $해결책$인 p$$( $m$) = $exp$ ($V$보다 이전 상태를 유도한다$.$^[42]이와는 대조적으로 최적의 제어는 $W{\displaystyle }$= ${\displaystyle 0}$ $[\displaystyle W=0}($즉, 흐름이 컬이 자유롭거나 세부적인 균형을 갖는다는 가정)에서 비용 함수가 주어진 흐름을 최적화한다.보통 이것은 거꾸로 된 콜모고로프 방정식을 푸는 것을 수반한다.^[43]

능동적 추론과 최적의 결정(게임) 이론

최적의 의사결정 문제(보통 부분적으로 관측 가능한 마르코프 의사결정 과정으로 공식화)는 효용 함수를 이전 신념에 흡수함으로써 능동적인 추론 내에서 처리된다.이 설정에서 효용성이 높은 상태(저비용)는 에이전트가 점유할 것으로 예상되는 상태를 말한다.모델 제어, 가변 자유 에너지를 최소화하는 정책(제어 시퀀스)^[44]이 높은 효용 상태로 이어진다는 숨겨진 상태와 생성 모델을 동일화함으로써.

신경생물학적으로 도파민 등 신경계수체는 주세포 인코딩 예측오차의 이득을 변조해 예측오차의 정밀도를 보고하는 것으로 간주된다.^[45]이는 예측^[46] 오류 보고 시 도파민의 역할 및 관련 계산 계정과 밀접하게 관련되어 있지만 공식적으로 구별된다.^[47]

능동적 추론과 인지신경과학

능동적 추론은 행동 관찰,^[48] 거울 뉴런,^[49] 사카데스와 시각적 탐색,^[50][51] 눈 움직임,^[52] 수면,^[53] 착시,^[54] 주의,^[37] 행동 선택,^[45] 의식,^[55][56] 히스테리^[57], 정신병을 포함한 인지 신경 과학, 뇌 기능 및 신경 정신의학의 다양한 문제들을 다루는데 이용되어 왔다.^[58]능동적 추론에서 작용에 대한 설명은 흔히 뇌가 갱신할 수 없는 '거품된 예측'을 가지고 있다는 생각에 따라 달라지며, 이러한 예측을 실현시키는 작용으로 이어진다.^[59]

참고 항목

• 작용별 인식
• Offendance – Offendance는 물체나 환경에 대한 조치의 가능성이다.
• 자동 복제 – 자동 재생 및 유지보수를 수반하는 시스템 개념
• 베이지안식 뇌기능 접근법
• 의사 결정 이론 – 대리인의 선택 연구
• 구체화된 인식
• 자유 에너지(동음이의)
• 정보 메트릭스
• 최적 제어 – 동적 시스템에서 원하는 출력을 얻는 수학적 방법
• 실습생이라고도 하는 적응형 시스템
• 예측 코딩 – 뇌 기능 이론
• 연습생
• 자체 조직 – 지역 상호 작용에 의한 질서 생성 프로세스
• 시너게틱스(하켄)
• 가변 베이지안 방법 – 베이지안 추론과 기계 학습에 사용되는 수학 방법
• '인 듯'의 철학

참조

외부 링크

• 행동 및 뇌과학 (앤디 클라크)