세이퍼트-반 캄펜 정리

수학에서, 때때로 반 캄펜의 정리라고 불린 대수 위상의 세이퍼트-반 캄펜 정리(Herbert Saifert와 Egbert van Kampen의 이름을 딴 이름)는$,$ 위상학적 공간 $X$의 기본 집단의 구조를, 커버하는 두 개의 개방된 경로 연결 $서브스페이스$의 기초 집단의 관점에서 표현하고$$ 있다$.$${\displaystyle \mathrm{따라서}}$ X $[\displaystyle X$ 따라서 단순한 것으로 구성된 공간의 기본 그룹의 계산에 사용할 수 있다.

기본 집단을 위한 반캄펜의 정리

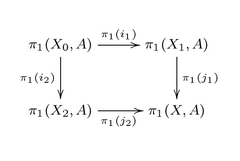
X는 두 개의 열린 공간과 연결된 경로로 연결된 서브스페이스₁ U, U₂.의 조합인 위상학적 공간이다. U₁ ∩ U는₂ 연결되고 비어 있지 않은 경로라고 가정하고, x는₀ U₁ ∩ U의₂ 포인트로서 모든 기본 집단의 기초가 될 것이다.The inclusion maps of U₁ and U₂ into X induce group homomorphisms ${\displaystyle j_{1}:\pi _{1}(U_{1},x_{0})\to \pi _{1}(X,x_{0})}$ and ${\displaystyle j_{2}:\pi _{1}(U_{2},x_{0})\to \pi _{1}(X,x_{0})}$.그런 다음 X ${\displaystyle {경로}_{}}$가 연결되고 $j{\displaystyle {}_{}}$ 1 ${\$및 $j$ ${\displaystyle {2\mathrm{}}_{}}$ ${\$2}가 역방향 푸시아웃 다이어그램을 형성한다$$.

자연 형태론 k는 이형성이다.즉, X의 기본 그룹은 ${\displaystyle {\pi \mathrm{}}_{}}$ 1${\displaystyle {}_{}}$(${\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$, x${\displaystyle {}_{}{0\mathrm{}}_{}}$ ) ${\displaystyle \pi _{1}(U_{1}\cap U_{2}x_{0}}}}}$의 합병과 함께₁ U와₂ U의 기본 그룹의 무료 제품이다$.$^[1]

보통 이 정리에 포함시킴으로써 유도된 형태론 자체가 주입적인 것이 아니며, 그 진술의 보다 정확한 버전은 집단의 밀어내기라는 측면에서 볼 수 있다.

반캄펜의 기본 그룹오이드 정리

불행히도 위에서 주어진 정리는 원의 근본 집단을 계산하지 못하는데, 이는 대수적 위상에서 가장 중요한 기본 예다.그 이유는 교차점이 연결된 두 개의 오픈 세트가 결합되어 원이 실현될 수 없기 때문이다.이 문제는 상황의 기하학적 도형에 따라 선택된 기본 그룹화 $\pi {\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$( ${\displaystyle X}$, A${\displaystyle }$) ${\displaystyle \pi _{1}(X,A)}$을(를) 사용하여 해결할 수 있다.따라서 원의 경우 두 개의 기준점을 사용한다.^[2]

This groupoid consists of homotopy classes relative to the end points of paths in X joining points of A ∩ X. In particular, if X is a contractible space, and A consists of two distinct points of X, then ${\displaystyle \pi _{1}(X,A)}$ is easily seen to be isomorphic to the groupoid often written ${\displaystyle {\$두 개의 꼭지점과 두 꼭지점 사이에 정확히 하나의 형태론을 갖는$$ $mathcal$ {$I}.$이 조로이드는 조로이드 이론에서 정수의 조와 유사한 조로이드 이론에서 역할을 한다.^[3]groupoid$$ $I{\displaystyle \mathcal{}}$ ${\$ {$I}$도 groupoids에 대해 호모토피 개념을 허용한다. 즉, groupoids 범주의 단위 간격 객체다.

연결되지 않은 두 공간의 연결된 결합과 기준점 집합

groupoids의 범주는 모든 콜리미트, 특히 모든 푸시아웃을 인정한다.

정리.위상학적 공간 X를 두 개의 서브 스페이스 X₁, X의₂ 내부로 덮게 하고 A를₁ X₂, X₀, X₁ = X의₂ 각 경로 구성요소를 충족하는 세트로 한다.그 후 A는 X의 각 경로 성분과 포함에 의해 유도된 형태론의 도표 P를 충족한다.

groupoids 범주에 있는 푸시아웃 다이어그램이다.^[4]

이 정리는 토폴로지로부터 대수학으로의 전환을 제공하며, 기초 그룹화 ${\displaystyle {oid\mathrm{}}_{}}$ 1 ${\displaystyle {}_{}X}$, A${\displaystyle }$) ${\displaystyle \pi _{1}(X,A$ 그런 다음 대수학과 결합학을 사용하여 어떤 기초 지점에서 기초 그룹을 결정해야 한다.

그 정리의 한 가지 해석은 호모토피 1형식을 계산한다는 것이다.그 효용성을 보기 위해 X가 연결된 경우를 쉽게 찾을 수 있지만 각각 402개의 경로 구성요소와 1004개의 경로 구성요소를 가진 두 개의 서브스페이스의 내부 결합이다."근본적 그룹"을 위한 계산 도구로서 이 정리를 해석하려면 '결합적 그룹론'^[5][6]의 어느 정도 개발이 필요하다.이 정리는 정수의 그룹이 그룹오이드 I ${\$에서 그룹오이드 $I{\displaystyle \mathcal{}}$ {\displaystyle {\mathcal{I}}}로부터 얻어지기 때문에 원의 기본 그룹을 정수의 그룹으로 계산하는 것을 의미한다.

X가 {${\displaystyle {}_{}}$ ${\displaystyle {\lambda }_{}}$ :${\displaystyle {}_{}\mathrm{\lambda }}$ ${\displaystyle \in }$ } } }${\displaystyle }$}$$} {\$displaystyle \{U_${\lambda$\}:\lambda \in$ \$lambda$\}}의 하위 집합의 내부$$ 조합에 의해 가려질 때 마지막 정리 버전이 있다.^[7][8]

결론은 A가 세트 ${\displaystyle U_{}}$ ${{\$의 1,2,3배 교차로에서 각각의 경로 구성요소를 충족하면, A는 X의 모든 경로 구성요소와 도표의 모든 경로 구성요소를 충족한다는 것이다.

${\displaystyle \bigsqcup _{(\lambda ,\mu )\in \Lambda ^{2}}\pi _{1}(U_{\lambda }\cap U_{\mu },A)\rightrightarrows \bigsqcup _{\lambda \in \Lambda }\pi _{1}(U_{\lambda },A)\rightarrow \pi _{1}(X,A)}$

포함에 의해 유도된 형태는 조로이드 범주에서 동일하다.

[...] 사람들은 기본적인 그룹으로 계산할 때 상황의 대칭에 따라 불변하는 점 전체를 교묘히 선택하는 대신, 하나의 기준점을 고정하는데 있어서 여전히 완강하게 고집하고 있다.특정 상황(기본 그룹에 대한 하강 이론 ab la Van Kampen 등)에서 적절한 기준점 패킷에 대해 기초적인 그룹노이드와 작업하는 것은 훨씬 우아하고 심지어 무언가를 이해하는 데 필수적이다 [...]

— Alexander Grothendieck, Esquisse d'un Programme (Section 2, English translation)

등가제식

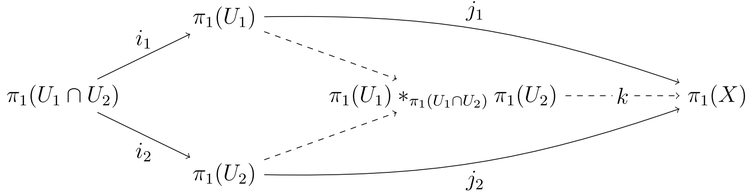
In the language of combinatorial group theory, if ${\displaystyle X}$ is a topological space; ${\displaystyle U}$ and ${\displaystyle V}$ are open, path connected subspaces of ${\displaystyle X}$; ${\displaystyle U\cap V}$ is nonempty and path-connected; and ${\displaystyle w\in U\cap V}$;then ${\displaystyle \pi _{1}(X,w)}$ is the free product with amalgamation of ${\displaystyle \pi _{1}(U,w)}$ and ${\displaystyle \pi _{1}(V,w)}$, with respect to the (not necessarily injective) homomorphisms ${\displaystyle I$$:\pi _{1}(U\cap V,w)\to \pi _{1}(U,w)}$ and ${\displaystyle J:\pi _{1}(U\cap V,w)\to \pi _{1}(V,w)}$. Given group presentations:

${\displaystyle {\begin{aligned}\pi _{1}(U,w)&=\langle u_{1},\cdots ,u_{k}\mid \alpha _{1},\cdots ,\alpha _{l}\rangle \\\pi _{1}(V,w)&=\langle v_{1},\cdots ,v_{m}\mid \beta _{1},\cdots ,\beta _{n}\rangle \\\pi _{1}(U\cap V,w)&=\langle w_{1},\cdots ,w_{p}\mid \gamma _{1},\cdots ,\gamma _{q}\rangle \end{aligned}}}$

합병은 다음과 같이 나타낼^[9] 수 있다.

${\displaystyle \pi _{1}(X,w)=\좌측\langle u_{1},\cdots,u_{k},v_{1},{m}\좌측 \alpha _,\cdots,\l},\cdots _{n},I(w_{1})J(w_{1})^{-1},\cdots,I(w_{p})J(w_{p})^{-1}\right.\right\rangele .}$

범주 이론에서 $\pi {\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$( ${\displaystyle X}$, ${\displaystyle w}$) ${\displaystyle \pi _{1}(X,w)}$은(는) 그룹의 범주에서 푸시아웃이다.

$\displaystyle \pi _{1}(U,w)\gets \pi _{1}(U\cap V,w)\to \pi _{1}(V,w).}$

예

2-sphere

반 캄펜의 정리를 이용하여 더 단순한 공간으로 분해될 수 있는 위상학적 공간의 기본 집단을 계산할 수 있다.For example, consider the sphere ${\displaystyle S^{2}}$. Pick open sets ${\displaystyle A=S^{2}\setminus \{n\}}$ and ${\displaystyle B=S^{2}\setminus \{s\}}$ where n and s denote the north and south poles respectively.그러면 A, B, A ∩ B가 오픈 경로로 연결된 집합이라는 속성을 갖게 된다.따라서 우리는 A와 B에 A와 B를 포함한 정류 도표가 있고, 그 다음에 A와 ${\displaystyle B^{}}$를 $S{\displaystyle {}^{}}$ 2 ${\$에 포함하는 도표가 있으며, 각$$ 서브 스페이스의 기본 그룹 사이에 동형성의 해당 도표가 있음을 알 수 있다.반 캄펜의 정리를 적용하면 그 결과가 나온다.

${\displaystyle \pi _{1}(S^{2})=\pi _{1}(A)\cdot \pi _{1}(B)/\ker(\Phi).}$

단, A와 B는 모두 R과² 동질적으로 연결되어 있어 A와 B는 모두 사소한 기본집단을 가지고 있다.이것으로부터 S ${\displaystyle {2\mathrm{}}^{}}$ ${\$의 기본 집단은 사소하다는$$ 것이 명백하다.

웨지 합 공간

Given two pointed spaces ${\displaystyle (X,x)}$ and ${\displaystyle (Y,y)}$ we can form their wedge sum, ${\displaystyle (X\vee Y,p)}$, by taking the quotient of ${\displaystyle X\coprod Y}$ by identifying their two basepoints.

If ${\displaystyle x}$ admits a contractible open neighborhood ${\displaystyle U\subset X}$ and ${\displaystyle y}$ admits a contractible open neighborhood ${\displaystyle V\subset Y}$ (which is the case if, for instance, ${\displaystyle X}$ and ${\displaystyle Y}$ are CW complexes), then we ca $X{\displaystyle }$ ${\displaystyle \vee }$ ${\displaystyle V}$ ${\displaystyle$ X$\ve V}$ 및 $U$ ${\displaystyle \vee }$ ${\displaystyle Y}$ ${\displaystyle U\ve Y}$을 두 개의 오픈 세트로$$ 취함으로써$$ Van Kampen 정리를 $X{\displaystyle }$ ${\displaystyle \vee }$ Y ${\displaystyle Y}$에 적용하고, 쐐기의 기본 그룹은 다음 두 공간의 기본 그룹의 자유로운 산물이라고 결론을 내린다.

${\displaystyle {\pi }_{}}$ ${\displaystyle {1\mathrm{}}_{}}$( ${\displaystyle X}$ ${\displaystyle \vee }$ ${\displaystyle Y}$, p${\displaystyle }$) ${\displaystyle \cong }$ ${\displaystyle {1\mathrm{}}_{}}$ (${\displaystyle {}_{}X}$, ${\displaystyle x}$) ${\displaystyle \ast }$ ${\displaystyle {1\mathrm{}}_{}}$(${\displaystyle Y}$, ${\displaystyle y}$ ) { 1 (${\displaystyle {}_{}}$ , y )$displaystyle \pi _{1}(X\$vee $Y,p)\cong \pi _{1}(X,x)*\pi _{1}(Y,y$

오리엔테이블 속 g

보다 복잡한 예로는 N개 속 표면 그룹으로 알려진 n개 방향 표면 S의 기본 집단의 계산이다.표준 기본 다각형을 사용하여 S를 구성할 수 있다.첫 번째 열린 집합 A의 경우 다각형의 가운데에 있는 디스크를 선택하십시오.A의 중심점 S의 보수가 되도록 B를 선택한다.그러면 A와 B의 교차점은 환형인데, 동그라미와 같은 (그래서도) 원과 같은 근본 집단을 갖는다고 알려져 있다.Then ${\displaystyle \pi _{1}(A\cap B)=\pi _{1}(S^{1})}$, which is the integers, and ${\displaystyle \pi _{1}(A)=\pi _{1}(D^{2})={1}}$.따라서 $\pi {\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$( ${\displaystyle A}$ ${\displaystyle \cap }$ B${\displaystyle }$) ${\$$displaystyle \pi _$${1}($$A\cap$ $B)}$을(를$)$ ${\displaystyle {\pi \mathrm{}}_{}}$ 1$$( ${\displaystyle A}$)에$$ 포함시키면 모든 발전기가 사소한 요소에 전송된다$$.그러나 $\pi {\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$(${\displaystyle A}$ ${\displaystyle \cap }$ B${\displaystyle }$) ${\displaystyle \pi _{1}(A\cap$ B$)}$을(를) $\pi {\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$(${\displaystyle B}$)$${\$displaysty \pi _{1}(B)}$에 포함하는 것은 사소한 일이$$ 아니다.이를 이해하려면 먼저 ${\displaystyle {\pi \mathrm{}}_{}}$ 1${\displaystyle {}_{}}$($){\displaystyle \pi _{1}(B)}$을 계산해야 한다$.$ 이는 수축 B(1 점을 삭제한 S)를 라벨에 붙인 가장자리에 변형시킬 수 있기 때문에 쉽게 이루어진다.

${\displaystyle A_{1}B_{1}{1}A_{1}^{-1}B_{1}^{-1}A_{2}B_{2}A_{2}^{-1}B_{2}^{-1}^{-1}\cdots A_{n}B_{n}A_{n}^{-1}B_{n}^{1}.}$

This space is known to be the wedge sum of 2n circles (also called a bouquet of circles), which further is known to have fundamental group isomorphic to the free group with 2n generators, which in this case can be represented by the edges themselves: ${\displaystyle \{A_{1},B_{1},\cdots ,A_{n},B_{n$$\}\}\backslash \}\}$이제 반캄펜의 정리를 적용할 충분한 정보를 확보했다.발전기는 루프${\displaystyle }${ ${\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$,${\displaystyle {}_{}}$B ${\displaystyle {1\mathrm{}}_{}}$,${\displaystyle {}_{}\cdots }$, A ${\displaystyle n_{}}$, ${\displaystyle {}_{}}$ ${\displaystyle n_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle \{A_{1},B_{1},\cdots ,A_{n},B_{n}\}}}($A는 단순히 연결되어 있기 때문에 발전기에 기여하지 않는다)이며, 정확히 한 가지 관계가 있다.

${\displaystyle A_{1}B_{1}{1}A_{1}^{-1}B_{1}^{-1}A_{2}B_{2}A_{2}^{-1}B_{2}^{-1}^{-1}\cdots A_{n}B_{n}A_{n}^{-1}B_{n}^{-1}=1}$

생성기 및 관계를 사용하여 이 그룹이 표시됨

${\displaystyle \left\langle A_{1},B_{1},\cdots,A_{n},B_{n}\왼쪽 A_{1}B_{1}{1}A_{1}^{-1}B_{1}^{1}^{-1}\cdots A_{n}B_{n}A_{n}^{-1}B_{n}^{-1}\right.\right\rangele .}$

단순연결성

X가 U ∩ V와 U ∩ V가 비어 있지 않고 경로로 연결된 두 개의 오픈 커넥티드 세트 U와 V의 결합으로 쓰여질 수 있는 공간이라면 X는 간단히 연결된다.^[10]

일반화

위에서 설명한 바와 같이, 이 정리는 로널드 브라운에 의해 기본 그룹화 $\pi {\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$(${\displaystyle X}$,${\displaystyle A}$ $){\displaystyle \pi _{1}(X,A)}$를 베이스 포인트의 집합 A에 사용함으로써 비연결 케이스까지 확장되었다.임의의 커버에 대한 정리는 A가 커버 세트의 세 가지 교차점을 모두 충족한다는 제한과 함께 브라운과 압둘 라작 살레에 의해 논문에서 주어진다.^[11]기본 집단을 위한 정리나 증명도 있지만, 어떤 그룹형 방법을 사용하여 J. Peter May의 저서에도 제시되어 있다.^[12]겹치는 세트가 두 개 이상 가능하지만 A와 함께 싱글톤이 있는 버전은 아래의 앨런 해쳐의 책 정리 1.20에도 제시되어 있다.

요르단 곡선 정리, 커버 공간, 궤도 공간 등에 대한 기본적 그룹오이드의 적용은 로널드 브라운의 저서에 제시되어 있다.^[13]궤도 공간의 경우 작용의 모든 고정점을 포함시키기 위해 A를 취하는 것이 편리하다.여기의 예는 원에 대한 결합 작용이다.

호모토피 종류에 대한 정보를 산출하는 고차원적인 형태의 정리에 대한 참조는 고차원적인 집단 이론과 그룹오이드에 관한 기사에 제시되어 있다.^[14]따라서 비아벨주의 두 번째 상대적 호모토피 그룹을 계산하는 2차원 반 캄펜 정리는 로널드 브라운과 필립 J. 히긴스에 의해 주어졌다.^[15]전체 계정과 모든 차원에 대한 확장은 브라운, 히긴스, 라파엘 시베라가,^[16] N-Cube의 공간에 대한 확장은 로널드 브라운과 장 루이스 로데이가 제공한다.^[17]

기초단체도 대수 기하학에서 등장하며 알렉산더 그로텐디크의 첫 세미니어 데 게오메트리 알제브리크(SGA1)의 주요 주제다.밴 캄펜의 정리 버전이 그곳에 나타나며, 대수학적 위상, 즉 하강 이론에서와는 상당히 다른 선을 따라 증명된다.대수학적 위상에서도 이와 유사한 증거가 작용한다.^[18]

참고 항목

• 고차원대수학
• 상위분류론
• 유사공작법
• 로널드 브라운 (마테마틱스)

메모들

참조

• 알렌 해처, 대수학 위상(2002) 케임브리지 대학 출판사, 캠브리지, 시이+544 pp.ISBN 0-521-79160-X 및 ISBN 0-521-79540-0
• 피터 메이, 대수학 위상에서의 간결한 과정.(1999년) 시카고 프레스대학 ISBN 0-226-51183-9 (제2.7절은 조로이드의 범주에 있는 콜리밋으로서 정리를 범주-이론적으로 제시한다.)
• 로널드 브라운, 조로이드와 반 캄펜의 정리, 프락. 런던 수학. Soc. (3) 17 (1967) 385–401.
• 여러 기준점에 대한 수학 오버플로 토론
• Ronald Brown, Topology and Groupoids(2006) Booksurge LLC ISBN 1-4196-2722-8
• R. Brown과 A. Razak, 연결되지 않은 공간의 결합을 위한 Van Kampen 정리, Archiv.수학. 42 (1984) 85–88. (이 논문은 아마도 최적의 정리 버전, 즉 덮개 집합의 모든 1.2-3배 교차점의 모든 경로 구성요소를 충족하는 임의의 개방 커버와 기준점 집합의 그룹형 버전을 제공한다.)
• P.J. 히긴스, 카테고리 및 그룹오이드(1971) 반 노스트롱드 라인홀드
• 로널드 브라운, 고차원 집단 이론(2007) (다중적인 그룹노이드가 포함된 고차원 반캄펜 이론에 대한 넓은 시야를 확보한다.)
• Greenberg, Marvin J.; Harper, John R. (1981), Algebraic topology. A first course, Mathematics Lecture Note Series, vol. 58, Benjamin/Cummings, ISBN 0805335579
• 세이퍼트, H, Construction dreli drilli dimenser Geschlossener Raume.베리히테 삭스.아카드, 라이프치히, 수학-피. Kl. (83) (1931) 26–66.
• E. R. 반 캄펜일부 관련 공간의 기본 그룹 간의 연결.미국 수학 저널, 제55권(1933), 페이지 261-267.
• 브라운, R, 히긴스, P. J, 몇몇 관련 공간의 두 번째 상대 호모토피 그룹들 간의 연결에 대해서, Proc.런던 수학.Soc. (3) 36 (1978) 193–212.
• Brown, R., Higgins, P. J. and Sivera, R.. 2011, EMS Tracts in Mathematics Vol.15 (2011) Nonabelian Algebraic Topology: filtered spaces, crossed complexes, cubical homotopy groupoids; (The first of three Parts discusses the applications of the 1- and 2-dimensional versions of the Seifert–van Kampen Theorem.후자는 비아벨리안적 두 번째 상대적 호모토피 그룹과 사실 호모토피 2 유형의 계산을 허용한다.두 번째 파트에서는 교차 콤플렉스에 대해 상위 호모토피 판 캄펜 정리를 적용한다.)
• "Van Kampen's theorem result". PlanetMath.
• R. Brown, H. Kamps, T. Porter : Hausdorff 공간 II의 호모토피 이중 그룹: Van Kampen 정리, 범주 이론 및 적용, 14 (2005) 200–220.
• 딜런 G.L. 알레그레티, 심플리컬 세트, 밴 캄펜의 정리(위상학적 공간과 심플리컬 세트에 적용된 밴 캄펜의 정리 일반화 버전을 논함)
• R. Brown과 J.-L. Loday, 토폴로지 26 (1987) 311–334의 "공간 다이어그램에 대한 반 캄펜 이론".

이 기사는 Creative Commons Accounting/Share-Alike License에 따라 허가된 PlanetMath에 대한 Van Kampen의 정리로부터 얻은 자료를 통합하고 있다.

외부 링크

• 위키미디어 커먼스의 세이퍼트-반 캄펜 정리 관련 매체