트래픽 플로우

수학 및 교통 공학에서 교통 흐름은 여행자(보행자, 자전거 이용자, 운전자 및 그들의 차량 포함)와 인프라(고속도로, 표지판 및 교통 제어 장치 포함) 사이의 상호작용에 대한 연구로, 교통 흐름의 효율적인 이동과 함께 최적의 교통 네트워크를 이해하고 개발하는 것을 목적으로 한다.트래픽과 최소한의 트래픽 폭주 문제를 해결합니다.

역사

교통 흐름의 수학적 이론을 제시하려는 시도는 프랭크 나이트가 교통 균형 분석을 처음 만들었던 1920년대로 거슬러 올라가며, 1952년 워드롭의 제1원칙과 제2원칙으로 다듬어졌다.

그럼에도 불구하고, 상당한 컴퓨터 처리 능력의 출현에도 불구하고, 현재까지 실제 흐름 조건에 일관되게 적용될 수 있는 만족스러운 일반 이론은 없었다.현재의 트래픽 모델에서는 경험적 기술과 이론적 기술이 혼재되어 있습니다.이러한 모델은 교통 예측으로 개발되며, 차량 사용 증가, 토지 이용의 변화 또는 교통 모드의 변화(예를 들어 사람들이 버스에서 기차 또는 자동차로 이동하는 경우)와 같은 제안된 지역 또는 주요 변경 사항을 고려하고, 네트워크를 조정할 필요가 있는 혼잡 영역을 식별하기 위해 개발된다.

개요

다양한 운송 모드의 승객 수용량

도로 공간 요건

트래픽은 다수의 차량의 상호작용에 따라 복잡하고 비선형적인 방식으로 동작합니다.운전자들의 개별적인 반응으로 인해 차량은 단순히 역학의 법칙에 따라 상호작용하는 것이 아니라 차량 밀도에 따라 전방과 후방 모두에서 클러스터 형성과 충격파 ^{[citation needed]}전파를 나타낸다.교통 흐름의 일부 수학적 모델은 수직 큐 가정을 사용합니다. 이 가정에서는 정체된 링크를 따라 차량이 링크 길이를 따라 역류하지 않습니다.

프리플로우 네트워크에서는 트래픽흐름 이론이란 속도, 흐름 및 집중의 트래픽스트림 변수를 말합니다.이러한 관계는 주로 고속도로 또는 ^[1]고속도로에서 발견되는 중단 없는 트래픽 흐름에 관련되어 있습니다.차선당 마일당 12대 미만의 차량이 도로에 있을 경우 흐름 조건은 "자유"로 간주됩니다."안정적"은 때때로 차선당 마일 당 12~30대의 차량으로 묘사된다.밀도가 최대 질량 유량(또는 플럭스)에 도달하여 최적 밀도(1차선당 마일당 30대 이상의 차량)를 초과하면 교통 흐름이 불안정해지고 사소한 사고라도 지속적인 정지 및 정지 운전 상태가 발생할 수 있습니다."고장" 상태는 교통이 불안정해지고 ^[2]차선당 마일 당 67대의 차량이 초과될 때 발생합니다."Jam density"는 교통 흐름이 완전히 멈출 때, 보통 ^[3]차선당 마일당 185-250대의 차량 범위 내에서 극심한 교통 밀도를 의미한다.

그러나 혼잡한 네트워크에 대한 계산은 더 복잡하며 실제 도로 수에서 얻은 경험적 연구와 외삽에 더 의존한다.이러한 요소는 도시나 교외에 있는 경우가 많기 때문에, 다른 요인(도로 사용자 안전 및 환경 고려 사항 등)도 최적의 조건에 영향을 미칩니다.

트래픽 스트림 속성

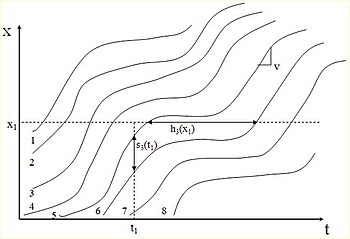
교통 흐름은 일반적으로 1차원 경로(예: 이동 차선)를 따라 제한됩니다.시간 공간 다이어그램은 시간 경과에 따른 경로를 따라 차량의 흐름을 그래픽으로 보여줍니다.수평축을 따라 시간이 표시되고 수직축을 따라 거리가 표시됩니다.시공간 다이어그램의 트래픽 흐름은 개별 차량의 개별 궤도선으로 표현된다.주어진 이동 차선을 따라 서로 뒤따르는 차량은 평행한 궤적을 가지며, 한 차량이 다른 차량을 통과할 때 궤적이 교차합니다.시간 공간 다이어그램은 주어진 도로 세그먼트의 시간 경과에 따른 교통 흐름 특성을 표시하고 분석하는 데 유용한 도구입니다(예: 교통 흐름 정체 분석).

트래픽 스트림을 시각화하는 세 가지 주요 변수는 속도(v^{[clarification needed]}), 밀도(k; 공간 단위당 차량 수), 흐름(q; 시간 단위당 차량 수)이다.

그림 1시간 공간 다이어그램

스피드

속도는 단위 시간당 커버되는 거리입니다.모든 차량의 속도를 추적할 수는 없기 때문에, 실제로 평균 속도는 일정 기간 동안 특정 지역의 차량을 표본 추출하여 측정됩니다.평균 속도의 정의는 "시간 평균 속도"와 "공간 평균 속도"의 두 가지입니다.

"시간 평균 속도"는 일정 기간 동안 도로의 기준 지점에서 측정됩니다.실제로는 루프 디텍터를 사용하여 측정됩니다.루프 검출기는 기준 영역에 분산되어 있으면 각 차량을 식별하고 속도를 추적할 수 있습니다.그러나 이 방법으로 구한 평균 속도 측정은 여러 차량에 걸쳐 평균화된 순간 속도가 동일한 거리에 ^{[clarification needed]}걸쳐 서로 다른 속도로 이동하는 차량의 이동 시간 차이를 고려하지 않기 때문에 정확하지 않다.
$v_{t}=(1/m)\sum _{i=1}^{m}v_{i$

여기서 m은 고정 지점을 통과하는 차량의 수를 나타내고_i v는 ih 차량의 속도를 나타냅니다.
"공간 평균 속도"는 전체 도로 세그먼트에서 측정됩니다.도로 세그먼트의 연속 화상 또는 동영상이 개별 차량의 속도를 추적해 평균 속도를 산출한다.이는 시간 평균 속도보다 더 정확한 것으로 간주됩니다.공간 평균 속도를 계산하기 위한 데이터는 위성 사진, 카메라 또는 둘 다에서 가져올 수 있습니다 $v_{s}=\left((1/n)\sum _{i=1}^{n}(1/v_{i})\right)^{-1}$ $v_{s}=\left((1/n)\sum _{i=1}^{n}(1/v_{i})\right)^{-1}$ s $v_{s}=\left((1/n)\sum _{i=1}^{n}(1/v_{i})\right)^{-1}$ ( $v_{s}=\left((1/n)\sum _{i=1}^{n}(1/v_{i})\right)^{-1}$ ( $v_{s}=\left((1/n)\sum _{i=1}^{n}(1/v_{i})\right)^{-1}$ / $v_{s}=\left((1/n)\sum _{i=1}^{n}(1/v_{i})\right)^{-1}$ ) $v_{s}=\left((1/n)\sum _{i=1}^{n}(1/v_{i})\right)^{-1}$ $v_{s}=\left((1/n)\sum _{i=1}^{n}(1/v_{i})\right)^{-1}$ $v_{s}=\left((1/n)\sum _{i=1}^{n}(1/v_{i})\right)^{-1}$ $v_{s}=\left((1/n)\sum _{i=1}^{n}(1/v_{i})\right)^{-1}$ n ( $v_{s}=\left((1/n)\sum _{i=1}^{n}(1/v_{i})\right)^{-1}$ 1 / $v_{s}=\left((1/n)\sum _{i=1}^{n}(1/v_{i})\right)^{-1}$ i ) - $v_{s}=\left((1/n)\sum _{i=1}^{n}(1/v_{i})\right)^{-1}$ { $display$ v $_$ { s } = \ $left$ ( $1$ / $n$ ) \ $sum _$ { i $v_{s}=\left((1/n)\sum _{i=1}^{n}(1/v_{i})\right)^{-1}$ = { $n$ } ( $1$ / $v$ { $i$ } \ $right$ ) $v_{s}=\left((1/n)\sum _{i=1}^{n}(1/v_{i})\right)^{-1}$ } }
여기서 n은 도로 세그먼트를 통과하는 차량의 수를 나타냅니다.

따라서 "공간 평균 속도"는 속도의 조화 평균이다. $시간$ 평균 속도는 공간 평균 속도보다 결코 작지 않습니다. $v_{t}=v_{s}+{\frac {\sigma _{s}^{2}}{v_{s}}}$ t $=$ $v_{t}=v_{s}+{\frac {\sigma _{s}^{2}}{v_{s}}}$ s + $v_{t}=v_{s}+{\frac {\sigma _{s}^{2}}{v_{s}}}$ $v_{t}=v_{s}+{\frac {\sigma _{s}^{2}}{v_{s}}}$ 2 $v_{t}=v_{s}+{\frac {\sigma _{s}^{2}}{v_{s}}}$ s { \ $displaystyle v _$ { t } = $v _$ { $s$ } + { \ $frac$ { \ displaystyle \ s }^{ $s }$ } $v_{t}=v_{s}+{\frac {\sigma _{s}^{2}}{v_{s}}}$ 。여기서 $\sigma _{s}^{2}$ s $\sigma _{s}^{2}$ { $displaystyle$ \ syle \ s }^{ $s$ ^{ s }^{ s}^{ s $}^{$ s}^{ s}}}} $is$ is is is is the the the the the the the^[4] the the the the

그림 2공간 평균 및 시간 평균 속도

시공간 다이어그램에서 차량의 순간 속도 v = dx/dt는 차량의 궤적을 따라 기울기와 같다.차량의 평균 속도는 차량이 도로 세그먼트에 진입하고 나가는 궤적 끝점을 연결하는 선의 기울기와 같다.평행 궤도 사이의 수직 분리(거리)는 선두 차량과 후속 차량 사이의 차량 간격이다.마찬가지로 수평 분리(시간)는 차량 전진도(h)를 나타낸다.시공간도는 각각 진로와 간격을 트래픽 흐름과 밀도에 관련짓는 데 유용하다.

밀도

밀도(k)는 도로 단위 길이당 차량 수로 정의된다.트래픽 흐름에서 가장 중요한 두 가지 밀도는 임계 밀도(k_c)와 방해 밀도(k_j)입니다.자유 흐름에서 얻을 수 있는 최대 밀도는 k인_c 반면_j, k는 폭주 상태에서 얻을 수 있는 최대 밀도입니다.일반적으로 잼 밀도는 임계 밀도의 5배입니다.밀도의 역방향은 간격(s)으로, 두 차량 사이의 중심-중심 거리입니다.

$k=svsfrac {1}{s}$

그림 3흐름 밀도 관계

그림 4흐름(q), 밀도(k) 및 속도(v)의 관계

주어진 시간(t₁)에서 도로 길이(L) 내의 밀도(k)는 n개 차량의 평균 간격의 역과 같다.

$K(L,t_{1})=param frac {n}{L}} = flac {1} {\bar {s}} （ t _ {1} } }$

시공간도에서는 영역 A에서의 밀도를 평가해도 된다.

$k(A)=frac {n}{L}} = flac {n,dt} {L,dt} = flac {tt} {\left A\right\vert }$

여기서 tt는 A의 총 이동시간입니다.

그림 5

흐름

흐름(q)은 시간 단위당 기준점을 통과하는 차량 수, 시간당 차량 수이다.흐름의 역수는 진행 방향(h)이며, 이는 공간의 기준점을 통과하는 ih 차량과 (i + 1)번째 차량 사이에 경과하는 시간입니다.congestion에서는 h는 일정하게 유지됩니다.교통체증이 생기면서 h는 무한대에 가까워진다.

${\displaystyle q=display,$

${{displaystyle q=1/h}$

간격(T) 동안 고정점(x₁)을 통과하는 흐름(q)은 m 차량의 평균 진로의 역과 같다.

$q(T,x_{1})=param frac {m}T}}=flac {1}{\bar {h}}(x_{1}}}}}$

시공간도에서는 영역 B에서 플로우를 평가해도 된다.

$q(B)=frac {m}{T}}=flac {m,dx}{T,dx}=flac {flac}{\left B\right\vert }$

여기서 td는 B 단위로 이동한 총 거리입니다.

그림 6

분석 방법

분석가는 물리학의 세 가지 주요 관측 척도에 해당하는 세 가지 주요 방법으로 문제에 접근합니다.

마이크로 스케일:가장 기본적인 수준에서 모든 차량은 개인으로 간주됩니다.방정식은 각각에 대해 기술할 수 있습니다.보통 상미분방정식(ODE)입니다.셀 오토메이션 모델도 사용할 수 있습니다.이 모델에서는, 도로가 셀로 분할되어 있고, 셀은 각각 움직이는 차를 포함하고 있거나 비어 있습니다.Nagel-Schreckenberg 모델은 그러한 모델의 단순한 예입니다.자동차가 상호작용하면서 교통 체증과 같은 집단 현상을 모델링할 수 있습니다.
거시적 척도:유체 역학 모델과 유사하게, 예를 들어 차량의 밀도 또는 평균 속도 등 일부 총 관심량에 대한 법칙의 균형을 맞추는 편미분 방정식 시스템을 사용하는 것이 유용한 것으로 간주된다.
메조스코픽(운동학적) 척도:세 번째 중간 가능성은 속도V(\ $displaystyle$ V $V$ 로 작동하는 $위치$ x $(\displaystyle$ x)에 $t$ $t$ 이 있을 가능성을 나타내는 $f(t,x,V)$ f $f(t,x,V)$ x, $){displaystyle$ f $(t, x$ , $V){$ displaystyle x $}$ 를 $f(t,x,V)$ $x$ 정의하는 것이다. 이 함수는 통계역학 방법에 따라,볼츠만 방정식과 같은 적분-미분 방정식을 사용하여 계산할 수 있습니다.

고속도로 교통 흐름 문제의 분석에 대한 공학적 접근법은 주로 경험적 분석(즉, 관측 및 수학적 곡선 적합)에 기초한다.미국 기획자들이 사용하는 한 가지 주요 참고 자료는 미국 국립과학아카데미의 일부인 교통연구위원회가 발간한 고속도로 용량 ^[5]매뉴얼이다.이는 큐잉의 영향을 포함하여 지연/흐름 함수를 사용하여 링크 전체 이동 시간을 사용하여 트래픽 흐름을 모델링할 것을 권장합니다.이 기술은 많은 미국 트래픽모델 및 유럽의 ^[6]SAURN 모델에서 사용됩니다.

유럽의 많은 지역에서, 교통 설계에 대한 하이브리드 경험적 접근방식이 사용되며, 매크로, 마이크로 및 메소스코픽 기능을 결합합니다.이동 경로의 안정적인 흐름 상태를 시뮬레이션하는 것이 아니라 일시적인 폭주 "수요 피크"가 시뮬레이션됩니다.이것들은, 업무일 또는 주말 내내 네트워크상에서 작은 「타임 슬라이스」를 사용해 모델화 됩니다.일반적으로 주행의 출발지와 목적지가 먼저 추정되며, 수학적 모델을 차량 유형별로 분류된 실제 트래픽 흐름의 관측된 카운트와 비교하여 보정되기 전에 트래픽 모델이 생성된다."행렬 추정"은 변경 전에 관측된 링크 카운트와 더 잘 일치하도록 모델에 적용되며, 수정된 모델은 제안된 방식에 대해 보다 현실적인 트래픽 예측을 생성하기 위해 사용됩니다.이 모델은 네트워크 주변의 일시적인 차단이나 사고의 영향을 이해하기 위해 여러 번(현재 기준, 경제 파라미터의 범위에 기초한 "평균일" 예측 및 민감도 분석에 의해 지원됨) 실행된다.모델을 통해 네트워크상의 다양한 유형의 차량 운전자들이 걸리는 시간을 합산하여 평균 연료 소비량과 배출량을 추론할 수 있다.

영국, 스칸디나비아 및 네덜란드 당국 관행의 대부분은 대형 계획을 위해 모델링 프로그램 CONTRAM을 사용하는 것으로, 영국의 교통 연구소의 후원 하에 수십 년 이상 개발되었으며 최근에는 스웨덴 도로청의 ^[7]지원을 받아 개발되었습니다.향후 수십 년간의 도로망 예측을 모델링함으로써, 시간 가치 및 기타 매개변수에 대한 추정치를 사용하여 도로망 변경의 경제적 편익을 계산할 수 있다.이러한 모델의 산출물은 비용 편익 분석 ^[8]프로그램에 입력될 수 있다.

누적 차량 수 곡선(N-곡선)

누적 차량 수 곡선인 N곡선은 일부 기준 ^[9]차량의 통과에서 측정된 특정 위치 x를 시간 t로 통과하는 누적 차량 수를 보여준다.만약 도착 시간 개별 차량)위치에 접근한 것으로 알려져 있어 이 곡선이고 이러한 도착 시간과 출발 시간을 획득하는 x. 위치해 출발 시간도 알려진 데이터 수집 시간을 요할 수 있었다:예로, 위치 X1및 X2에, 차량의 수를 계산할 2점 센서 설정할 수도 있t.될 수h각 차량이 X에₁ 도착하고 X에서₂ 출발하는 시간을 기록하면서 이 세그먼트를 통과합니다.결과 그래프는 한 쌍의 누적 곡선으로, 종축(N)은 X와₂ X의₁ 두 지점을 통과하는 누적 차량 수를 나타내고 수평축₂(t₁)은 X와 X로부터의 경과 시간을 나타냅니다.

그림 8단순 누적 곡선

그림 9.도착, 가상 도착 및 출발 곡선

차량이 X에서₁ X로 이동할₂ 때 지연이 발생하지 않는 경우, X 위치에서의₁ 차량 도착은 곡선₁ N으로 나타내고 X 위치에서의₂ 차량 도착은 그림 8에서 N으로 나타낸다₂.일반적으로 곡선₁ N은 위치 X에₁ 있는 차량의 도착 곡선이고 곡선₂ N은 위치₂ X에 있는 차량의 도착 곡선이다.는 교통 신호 녹색은 정류장 바의 접근에 X1위치와 수신 거리에서 그 교차점을 가로질러 X2는 자의적인 라인 예를 들어 있는 교차로에 이 차선signalized 접근법의 사용, 차량은 두가지 관점을 지연하게 될 것이고 그 먼 거리를 여행하는 시간eq 여행할 수 있다.ufree-flow 이동 시간에 맞춰야 합니다.그림 8의 두 개의 개별 곡선으로 그래픽으로 표시됩니다.

단, 신호등이 빨간색이면 차량이 정지바₁(X)에 도착해 적색신호에 의해 지연된 후 신호가 녹색이 된 후 얼마간 X를 건널₂ 수 있다.그 결과 신호등이 빨간색인 상태에서 교차로에 도착하는 차량이 많아짐에 따라 정지바에 대기열이 형성됩니다.따라서 교차로에 도착하는 차량이 여전히 대기열에 의해 방해받는 한, 곡선 N은 더 이상 차량이 위치₂ X에 도착한 것을 나타내지 않는다. 이제₂ 곡선₂ N은 차량이 위치 X에 실제로 도착한 것을 나타내며, 다시 말해 지연이 발생하지 않은 경우 차량이 위치 X에₂ 도착한 것을 나타낸다.교통 신호로부터의 지연을 고려한 차량의 위치₂ X 도착은 이제 그림 9의 Nµ ₂곡선으로 표현된다.

그러나 가상 도착 곡선의 개념은 결함이 있습니다.이 곡선은 트래픽 중단(즉, 빨간색 신호)으로 인한 큐 길이를 올바르게 나타내지 않습니다.모든 차량이 빨간색 신호등에 의해 지연되기 전에 여전히 정지 바에 도달하고 있다고 가정합니다.즉, 가상도착곡선은 정지바에 수직으로 차량이 쌓이는 모습을 나타낸다.교통신호가 녹색으로 바뀌면 이들 차량은 선입선출(FIFO) 순서로 운행됩니다.다만, 멀티 레인의 어프로치의 경우, 서비스 오더가 반드시 FIFO라고는 할 수 없습니다.그럼에도 불구하고, 해석은 개별 ^[10]차량의 총 지연 대신 평균 총 지연에 대한 우려 때문에 여전히 유용하다.

스텝 기능 vs 스무스 기능

그림 10.스텝 함수

신호등 예에서는 N곡선을 부드러운 함수로 나타냅니다.그러나 이론적으로는 수집된 데이터에서 N곡선을 그리면 단계 함수를 얻을 수 있습니다(그림 10).각 단계는 해당 시점에 ^[10]한 대의 차량이 도착하거나 출발하는 것을 나타냅니다.N-곡선이 여러 사이클을 포함하는 기간을 반영하여 더 큰 축척에 그려지면 개별 차량의 단계를 무시할 수 있으며 곡선은 부드러운 함수처럼 보입니다(그림 8).

트래픽 할당

그림 14.트래픽 할당을 위한 4단계 이동 수요 모델

교통 흐름 분석의 목적은 차량이 최대 도로 용량을 사용하여 가능한 한 짧은 시간 내에 목적지에 도달할 수 있도록 하는 모델을 만들고 구현하는 것이다.이것은 4단계 프로세스입니다.

세대 – 프로그램은 발생 횟수를 예측합니다.이를 위해 프로그램은 인구별 거주지역 통계데이터, 사업장 위치 등을 필요로 한다.
배포 – 생성 후 순서 1에서 찾은 위치 간에 서로 다른 출발지-목적지(OD) 쌍을 만듭니다.
모달 분할/모드 선택 – 시스템은 이용 가능한 교통수단(예: 자동차, 버스, 철도 등) 간에 인구 중 얼마나 많은 비율을 분할할 것인지를 결정해야 합니다.
경로 할당 – 마지막으로 최소 기준 규칙에 따라 차량에 경로가 할당됩니다.

이 사이클은 솔루션이 수렴될 때까지 반복됩니다.

최종 목표에 따라 이 문제에 대처하기 위해서는 주로 다음 두 가지 방법이 있습니다.

시스템 최적

즉, 전체 시스템 비용이 가능한 모든 할당 중 최소일 때 네트워크는 시스템 최적(SO) 상태가 됩니다.

System Optimum은 모든 차량의 경로가 시스템에 의해 제어되고 재루팅은 자원의 최대 활용과 최소 총 시스템 비용에 기초한다는 가정에 기초하고 있다(비용은 이동 시간으로 해석할 수 있다).따라서 System Optimum 라우팅 알고리즘에서는 특정 OD 쌍 간의 모든 루트는 동일한 한계비용을 가집니다.전통적인 교통 경제학에서, 시스템 최적성은 수요 함수와 한계 비용 함수의 균형에 의해 결정된다.이 접근법에서, 한계 비용은 대략적으로 교통 혼잡에서 기능이 증가하는 것으로 묘사됩니다.트래픽 플로우 어프로치에서 주행의 한계비용은 운전자가 경험하는 비용(지연시간, w)과 운전자가 나머지 ^[11]사용자에게 부과하는 외부성(e)의 합계로 나타낼 수 있다.

고속도로(0)와 대체 경로(1)가 있다고 가정하면 사용자는 이를 오프로드로 우회할 수 있습니다.운전자는 총 도착률(A(t), 고속도로 용량(μ₀), 대체 경로 용량(μ₁)을 알 수 있다.고속도로가 혼잡한 시점 t부터₀ 이용자 중 일부는 대체 경로로 이동하기 시작한다.단, t의 경우₁ 대체 루트에도 용량이 가득 차 있습니다.이제 운영자가 대체 경로를 사용하는 차량 수(N)를 결정합니다.최적의 차량 수(N)는 각 경로의 한계 비용을 동일하게 만들기 위해 변동 미적분을 통해 구할 수 있다.따라서 최적의 조건은 T₀ = T₁ + "₁ 입니다.이 그래프에서는 대체 경로의 큐가 프리웨이에서 클리어되기 전에 시간 단위를 ₁클리어해야 함을 알 수 있습니다.이 솔루션은 T와 T₁ 사이에 도착하는₁ 차량을 할당하는 방법을 정의하는 것이 아니라 최적의 솔루션이 고유하지 않다는 결론을 내릴 수 있습니다.만약 운영자가 고속도로의 정체를 원하지 않는다면, 운영자는 고속도로의 외부성과 대체 경로의 차이인 혼잡₀ 통행료 e - e를₁ 부과할 수 있다.이 경우 고속도로는 자유 유속을 유지하지만 대체 루트는 극심한 정체를 빚게 됩니다.

사용자 평형

즉, 모든 드라이버가 총 시스템 비용을 최소화하는지 여부에 관계없이 출발지와 목적지 사이의 가장 낮은 비용으로 경로를 선택할 때 네트워크는 사용자 균형(UE) 상태에 있습니다.

사용자 최적 균형은 모든 사용자가 다른 경로 옵션에서 소비되는 이동 시간에 기초하여 목적지로 향하는 자신의 경로를 선택한다고 가정합니다.사용자는 이동 시간이 가장 짧은 경로를 선택합니다.사용자 최적 모델은 종종 고속도로 병목현상에 의한 트래픽 할당에 대한 영향을 시뮬레이션할 때 사용됩니다.고속도로에서 정체가 발생하면 고속도로 주행의 지연 시간이 길어지고 이동 시간이 길어집니다.사용자의 최적 가정 하에서, 사용자는 특정 고속도로를 이용한 이동 시간이 도시 거리를 이용한 이동 시간과 같아질 때까지 기다리기로 선택하게 되며, 따라서 균형에 도달하게 된다.이 평형을 사용자 평형, 워드롭 평형 또는 내쉬 평형이라고 합니다.

그림 15.사용자 평형 트래픽모델

사용자 평형의 핵심 원칙은 주어진 OD 쌍 간에 사용되는 모든 경로가 동일한 이동 시간을 갖는 것입니다.대체 루트 옵션은 시스템 내의 실제 이동 시간이 해당 루트의 자유 흐름 이동 시간에 도달했을 때 사용할 수 있습니다.

하나의 대체 경로를 고려하는 고속도로 사용자 최적 모델의 경우, 일반적인 트래픽 할당 프로세스를 그림 15에 나타낸다.교통수요가 고속도로 수용능력을 밑돌면 고속도로의 지연시간은 0으로 유지된다.교통 수요가 정원을 초과하면 고속도로에 차량 행렬이 나타나 지연 시간이 증가합니다.일부 이용자는 고속도로 자유유통시간과 시내거리 자유유통시간의 차이에 도달하면 시내도로로 눈을 돌린다.고속도로에 머무는 이용자들은 시내 거리로 향하는 이용자들만큼 많은 이동 시간을 소비하게 될 것이다.이 단계에서 고속도로와 대체 경로의 이동 시간은 동일하게 유지됩니다.수요가 도로 용량 이하로 떨어지면, 즉 고속도로 주행 시간이 줄어들어 모든 이용자들이 고속도로에 머물게 될 것이다.부품 영역 1과 3의 합계는 대체 경로를 제공함으로써 이점을 나타냅니다.지역 4와 지역 2의 합계는 시스템의 총 지연 비용을 나타냅니다. 즉, 지역 4는 고속도로에서 발생하는 총 지연이고 지역 2는 시내 도로로 교통량을 이동함으로써 발생하는 추가 지연입니다.

구글 지도의 내비게이션 기능은 모든 사용자에게 최저 비용(이동 시간)으로 라우팅 옵션을 제공하기 때문에 사용자 평형에 기반한 동적 트래픽 할당의 전형적인 산업 애플리케이션이라고 할 수 있다.

시간 지연

User Optimum과 System Optimum 모두 솔루션에 소요된 시간 지연 접근법에 따라 두 가지 범주로 세분화할 수 있습니다.

예측 시간 지연

예측 시간 지연은 시스템 사용자가 지연이 얼마 동안 계속되는지 정확히 알고 있다고 가정합니다.예측 지연은 특정 congestion 레벨에 도달하는 타이밍과 그 시스템의 지연이 다른 시스템을 사용하는 타이밍보다 큰 타이밍을 인식하기 때문에 재루팅의 결정은 제시간에 할 수 있습니다.차량 계수-시간 다이어그램에서 시간 t에서의 예측 지연은 그림 16에서와 같이 도착과 출발 곡선 사이의 시간 t의 오른쪽에 있는 수평선 세그먼트이다. 해당 y 좌표는 시간 t에서 시스템을 떠나는 n번째 차량이다.

반응 시간 지연

리액티브 타임 지연은 사용자가 전방의 트래픽 상태를 모르는 경우입니다.사용자는 지연이 관찰되는 시점을 경험하기 위해 대기하며, 그 시점에서 재루팅 결정은 해당 경험에 대한 응답입니다.예측 지연은 반응 지연 방법보다 훨씬 더 나은 결과를 제공합니다.차량 계수-시간 다이어그램에서, 시간 t에서의 예측 지연은 그림 16에서와 같이 도착과 출발 곡선 사이의 시간 t의 왼쪽에 있는 수평선 세그먼트이다. 대응하는 y 좌표는 시간 t에 시스템에 진입하는 n번째 차량이다.

그림 16.예측 및 반응 시간 지연

가변 속도 제한 할당

이는 충격파를 제거하고 차량의 안전을 높이기 위한 향후 접근법입니다.이 개념은 상류와 하류 차량 간의 속도 차이에 따라 도로에서의 사고 위험이 증가한다는 사실에 기초한다.VSL 구현으로 줄일 수 있는 충돌 위험의 두 가지 유형은 후방 충돌과 차선 변경 충돌입니다.가변 속도 제한은 속도를 균질화함으로써 흐름이 ^[12]보다 일정해집니다.연구자들은 적절한 VSL 알고리즘을 구축하기 위해 다양한 접근방식을 구현했다.

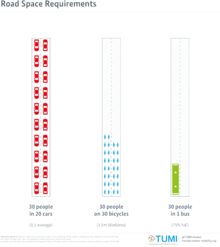
가변 속도 제한은 보통 도로의 센서가 정체 또는 기상 이벤트가 임계값을 초과했음을 감지할 때 제정됩니다.그런 다음 교통부가 관리하는 도로 위의 표지판(다이내믹 메시지 표지판)을 사용하여 도로 속도 제한을 5mph 단위로 줄입니다.이 과정의 목표는 사고 감소를 통한 안전성 향상과 도로 정체의 시작을 방지하거나 연기하는 것이다.이상적인 트래픽플로우는 전체적으로 느리지만 정지 및 정지 시간이 줄어들기 때문에 백엔드 크래시 및 레인 변경 크래시의 인스턴스가 줄어듭니다.VSL의 사용은 또한 정기적으로 이 과정이 전투를 목적으로 하는 혼잡 상태에서만 운송을 위해 허용된 숄더 랜을 사용한다.가변 속도 제한의 필요성은 오른쪽에 있는 흐름 밀도 다이어그램에 나와 있습니다.

일반 도로의 속도 흐름도

이 그림("일반 도로의 흐름 속도 다이어그램")에서 곡선의 지점은 흐름과 속도 모두에서 최적의 트래픽 이동을 나타냅니다.그러나 이 지점을 넘어서면 이동 속도가 빠르게 한계에 도달하고 급격히 감소하기 시작한다.이러한 급격한 속도 저하의 잠재적 위험을 줄이기 위해, 가변 속도 제한은 속도를 더 점진적인 속도로 줄여(5mph 증가) 정체/날씨로 인한 속도 저하에 더 많은 시간을 준비하고 적응할 수 있게 해 줍니다.균일한 주행 속도가 개발되면 운전자의 불규칙한 동작의 가능성이 감소하여 충돌이 발생합니다.

VSL 현장에서 수집된 과거 데이터를 통해 이 방법을 구현하면 사고 수가 20-30%^[12] 감소하는 것으로 파악되었다.

VSL은 안전과 효율에 대한 우려 외에도 배출량, 소음 및 연료 소비 감소와 같은 환경적 이점을 얻을 수 있습니다.이는 차량이 정체 ^[13]상태에서 흔히 볼 수 있는 것과 같은 일정한 가속 및 감속 상태보다 일정한 속도로 주행할 때 연료 효율이 더 높기 때문이다.

도로 교차로

도로 용량의 주요 고려사항은 교차로 설계와 관련이 있다.경사가 있는 교차로에서 완만하게 구부러진 도로에 긴 "직조 구간"을 허용함으로써, 차량은 종종 흐름에 큰 간섭을 일으키지 않고 차선을 가로질러 이동할 수 있습니다.그러나, 이것은 비싸고 많은 땅을 차지하기 때문에, 특히 도시나 매우 시골 지역에서 다른 패턴들이 종종 사용된다.대부분의 대형 모델은 교차로에 대해 조잡한 시뮬레이션을 사용하지만, 컴퓨터 시뮬레이션을 통해 특정 신호등 세트, 회선 및 흐름이 중단되거나 다른 유형의 도로 사용자 또는 보행자와 공유되는 기타 시나리오를 모델링할 수 있습니다.적절하게 설계된 접점은 낮 동안 일정 트래픽 밀도 범위에서 훨씬 더 많은 트래픽 흐름을 가능하게 할 수 있습니다.이러한 모델을 "인텔리전트 트랜스포트 시스템"에 연결함으로써 일련의 단계별 신호등을 통해 미리 정해진 속도로 중단 없는 차량 "패킷"으로 트래픽을 전송할 수 있습니다.영국의 TRL은 상세한 지오메트리와 시야선을 고려할 수 있는 소규모 국지적 체계를 위한 접합 모델링 프로그램을 개발하였다. 회진거리는 ARCADY, 우선 교차로는 PICADY, 신호는 OSCADY와 TRANSYT.Sidra, LinSig 및 Synchro와 같은 다른 많은 접합 분석 소프트웨어^[14] 패키지가 있습니다.

운동파 모형

운동파 모델은 1955년 라이트힐과 휘텀에 의해 교통 흐름에 처음 적용되었다.그들의 두 부분으로 이루어진 논문은 물의 움직임을 예로 들어 운동학적 파동 이론을 최초로 발전시켰다.후반부에는 "밀린 간선도로"의 교통으로 이론을 확장했다.본서에서는, 트래픽의 「힘」(흐름의 증가)과 특히 ^[15]보틀 넥에 의한 트래픽의 속도에의 영향의 개발에 주로 임했습니다.

저자들은 교통 흐름 이론에 대한 이전의 접근법에 대해 논의하는 것으로 시작했다.그들은 그 당시 실험적인 연구가 있었지만 "이 주제에 대한 이론적 접근은 초기 단계였다"고 지적한다.특히 John Glen Wardrop이라는 한 연구원은 주로 공간 평균 속도, 시간 평균 속도, "추월 시 흐름 증가 효과"와 그로 인해 발생할 수 있는 속도 감소와 같은 통계적 검사 방법에 대해 우려했다.이전의 다른 연구는 두 가지 개별 모델에 초점을 맞췄다. 하나는 교통 흐름과 관련된 교통 속도와 또 다른 하나는 차량 ^[15]간 이동 경로와 관련된 속도이다.

반면에 라이트힐과 휘텀의 목표는 "초음속 발사체에 대한 흐름 이론과 강의 홍수 이동에 대해 제시된" 새로운 연구 방법을 제안하는 것이었다.결과 모델은 앞서 언급한 관계인 속도 흐름과 속도-진행로를 모두 단일 곡선으로 포착하여 정체된 교통 흐름을 처리하는 능력과 관련된 도로의 모든 속성을 "집약"할 것이다.이들이 제시한 모델은 트래픽흐름과 집중(현재는 일반적으로 밀도라고 불립니다)을 관련짓습니다.그들은 "이 이론의 기본 가설은 도로의 어느 지점에서나 흐름 q(시간당 차량)가 농도 k(마일당 차량)의 함수라는 것입니다."라고 썼다.이 모델에 따르면, 교통 흐름은 "도로에 대한 상대 속도가 집중도에 대한 흐름 그래프의 기울기인 '운동파'를 따라 차량의 흐름을 통해 약간의 흐름의 변화가 역류한다"는 점에서 물의 흐름을 닮았다.저자들은 그러한 그래프의 예를 포함했다. 이 흐름 대 농도(밀도) 그래프는 오늘날에도 여전히 사용되고 있다(위 ^[15]그림 3 참조).

저자들은 이 흐름 집중 모델을 사용하여 진입하는 차량을 느리게 하는 충격파의 개념과 주변 조건을 설명했다.또한 새로운 모델과 관련하여 병목 현상과 교차점에 대해서도 논의했습니다.이러한 토픽 각각에 대해서, 플로우 집중도와 시공간도가 포함되어 있습니다.마지막으로, 저자들은 수용량에 대한 합의된 정의가 존재하지 않는다고 지적하고 "도로가 가능한 최대 흐름"으로 정의해야 한다고 주장했다.Lightill과 Whitham은 또한 자신들의 모델에 상당한 제한이 있다는 것을 인식했습니다. "연속 흐름" 접근 방식은 ^[15]많은 수의 차량에서만 작동하기 때문에 길고 혼잡한 도로에서만 사용할 수 있습니다.

교통 흐름 이론의 운동학적 파동 모델 구성 요소

교통 흐름 이론의 운동학적 파동 모델은 교통 파동의 전파를 재현하는 가장 단순한 동적 교통 흐름 모델입니다.기본도, 보존방정식, 초기조건의 3가지 요소로 구성되어 있습니다.보존의 법칙은 운동학적 파동 모델을 지배하는 기본 법칙이다.

${\frac k} {\frac x} = 0,$

키네마틱파 모델의 기본 다이어그램은 위의 그림 3에서 보듯이 트래픽흐름과 밀도를 관련짓습니다.다음과 같이 쓸 수 있습니다.

${{displaystyle {q}={F(k)}}$

마지막으로, 모델을 사용하여 문제를 해결하기 위해 초기 조건을 정의해야 합니다.경계는 k ${k(t,x)}$ ${k(t,x)}$ , ${k(t,x)}$ ) {k(t, ${k(t,x)}$ x)}(\displaystyle ${k(t,x$ 로 정의되며, 시간 및 위치의 함수로서 밀도를 나타냅니다.이러한 경계는 통상, 2개의 다른 형태를 취하기 때문에, Initial Value Problems(IVP; 초기값 문제)와 Boundary Value Problems(BVP; 경계값 문제)가 발생합니다.초기값 문제는 ${t}={0}$ ${k(0,x)}={g(x)}$ ( ${k(0,x)}={g(x)}$ ${t}={0}$ , ${k(0,x)}={g(x)}$ ) ${t}={0}$ ${k(0,x)}={g(x)}$ ${t}={0}$ ( ${k(0,x)}={g(x)}$ ) { $($ 0 ${t}={0}$ , x ) = {g ( x )} = {g ( x )} ${k(0,x)}={g(x)}$ ${g(x)}$ ( ${g(x)}$ ) \ $display$ style { $g ( x$ ) }는 ${g(x)}$ 지정된 밀도 함수입니다 $.$ 경계값 문제는 x ${k(t,0)}={g(t)}$ $({$ ${x=0}$ 의 ${x=0}$ 밀도를 나타내는 ${g(t)}$ g $({$ ${g(t)})$ 를 ${g(t)}$ 제공합니다 ${k(t,0)}={g(t)}$ k( $,0$ )}={ $g(t$ 이 모델은 트래픽 흐름에서 많은 용도로 사용됩니다.주요 용도 중 하나는 트래픽 병목현상을 모델링하는 것입니다(다음 항에서 설명).

트래픽 병목 현상

교통 병목현상은 도로 설계, 신호등 또는 사고로 인한 도로상의 교통 장애입니다.병목에는 일반적으로 고정 병목과 이동 병목의 두 가지 유형이 있습니다.정지 병목은 도로의 협소, 사고 등 정지 상태에서 발생하는 교란으로 인해 발생하는 병목입니다.반면에 이동 병목현상은 차량의 업스트림에 있는 차량의 장애를 일으키는 차량 또는 차량 거동입니다.일반적으로 이동 병목현상은 무거운 트럭에 의해 발생하는데, 이 트럭은 가속력이 떨어지고 차선이 변경될 수 있기 때문이다.

그림 16.

병목 현상은 트래픽 흐름, 즉 차량의 평균 속도에 영향을 미치기 때문에 중요한 고려 사항입니다.병목 현상의 주된 결과는 도로의 수용량이 즉시 감소하는 것입니다.연방 고속도로 당국은 전체 정체 중 40%가 병목 현상으로 인한 것이라고 밝혔습니다. 그림 16은 다양한 정체 원인에 대한 원형 차트를 보여줍니다.

정지 병목

그림 18.

정지 상태의 병목현상의 일반적인 원인은 복수 레인의 차선이 상실되었을 때 발생하는 차선 저하입니다.이로 인해 종점 차선의 차량 트래픽이 다른 차선으로 병합됩니다.

이동 병목

앞서 설명한 바와 같이 이동 병목현상은 차량이 느리게 이동하기 때문에 교통에 지장을 초래합니다.이동 병목은 활성 병목일 수도 있고 비활성 병목일 수도 있습니다.이동보틀 넥에 의한 저하용량(q_u)이 실제 차량 하류용량(μ)보다 크면 이 보틀 넥을 활성보틀 넥이라고 한다.

고전적인 교통 흐름 이론

일반적으로 받아들여지는 트래픽 및 교통 이론의 기초 및 방법론은 다음과 같습니다.

Lightill-Whitham-Richards(LWR) 모델은 1955-56년에 도입되었습니다.^[15]^[16]Daganzo는 LWR ^[17]모델과 일치하는 세포전송모델(CTM)을 선보였다.
교통 흐름의 불안정성으로 인해 차량 속도의 국지적 감소가 증가하게 됩니다.General Motors(GM; 제너럴 모터스) 자동차 추종 모델에서는 Herman, Gazis, Montroll, Potts ^[18]^[19]및 Rothery가 1959-61년에 이러한 고전적인 교통 흐름 불안정성을 도입했습니다.GM 모델의 고전적인 트래픽 흐름 불안정성은 Gips 모델, Payne 모델, Newell의 최적 속도(OV) 모델, Wiedemann 모델, Whitham의 모델, Nagel-Schreckenberg(NaSch) 셀룰러 오토매톤(CA) 모델 등 수많은 트래픽 흐름 모델에 통합되었습니다.OV 모델, Treiber의 IDM, Krauß 모델, Aw-Rascle 모델 및 기타 잘 알려진 미시적이고 거시적인 트래픽 흐름 모델들, 이것들은 교통 엔지니어와 연구자들에 의해 널리 사용되는 트래픽 시뮬레이션 도구의 기초이다. (예: 검토 참조^[20]).
고속도로 용량을 특정 가치로 이해하는 것.도로 용량에 대한 이러한 이해는 1920-35년에 도입되었을 가능성이 있습니다( 참조).현재, 고속도로 병목 지점에서의 자유 흐름의 고속도로 용량은 확률적 값이라고 가정한다.그러나 고속도로 용량에 대한 기존의 이해에 따라, 주어진 순간에 이 확률적 고속도로 용량의 특정 값이 하나만 있을 수 있다고 가정한다(책 참조^[22]).
Wardrop의 트래픽 및 교통 네트워크의 최적화 및 ^[23]제어를 위한 사용자 평형(UE) 및 시스템 최적(SO) 원칙.

대안: Kerner의 3상 트래픽 이론

3상 교통이론은 1990년대^[24]^[25]^[26] 말 보리스 케너에 의해 만들어진 교통 흐름의 대안 이론이다(검토는 책을^[27]^[28]^[29] 참조).아마도 3상 이론의 가장 중요한 결과는 어떤 경우에도 병목현장에서 자유 흐름의 고속도로 용량 범위가 존재한다는 것입니다.용량 범위는 일부 최대 용량과 최소 용량 사이입니다.3상 교통 이론에서 보틀 넥에서의 자유 흐름의 고속도로 용량 범위는 기본적인 교통 이론과 모순되며, 교통 관리 및 교통 제어를 위한 방법에는 언제든지 보틀 넥에서의 자유 흐름의 특정 결정론적 또는 확률적 고속도로 용량이 존재한다고 가정한다.교통 현상에 대해 배운 적이 없는 비전문가들은 책에서 ^[30]케너의 3상 교통 이론의 출현으로 이어지는 실제 측정된 차량 교통 현상에 대한 간략한 설명을 찾을 수 있다. ^[31]케너 이론의 일부 공학적 적용은 이 책에서 찾을 수 있다.

Newell-Daganzo 병합 모델

Newell-Daganzo 병합 모형 및 변수 다이어그램

두 개의 분기 도로를 출발하여 단일 도로를 통해 단일 흐름으로 합류하는 교통 흐름의 경우, 합류 프로세스와 도로의 각 분기 상태를 결정하는 것은 교통 엔지니어에게 중요한 작업이 됩니다.Newell-Daganzo 병합 모델은 이러한 문제를 해결할 수 있는 좋은 방법입니다.이 단순한 모델은 Gordon Newell의 병합^[32] 과정 설명과 Daganzo의 세포 전송 ^[33]모델의 결과입니다.모델을 적용하여 도로의 두 분기와 도로의 각 분기의 통계에서 나오는 흐름을 결정하려면 도로의 두 입력 분기의 용량, 출구 용량, 도로의 각 분기의 수요 및 단일 도로의 차선 수를 알아야 한다.합류 비율은 도로의 양쪽 지선이 혼잡한 조건에서 작동할 때 두 입력 흐름의 비율을 결정하기 위해 계산됩니다.

합류 ^[34]프로세스의 간략화된 모델에서 알 수 있듯이 시스템의 출구 용량은 μ, 차도의 두 입력 분기 용량은 μ 및₁₂ μ, 차도의 각 분기 수요는 q 및₂^D q로₁^D 정의된다.q와₂ q는₁ 머지 프로세스를 통과하는 흐름인 모델의 출력입니다.모델의 프로세스는 도로의 두 입력 분기의 총 용량이 시스템의 기존 용량인₁ μ+μ₂ µμ보다 작다는 가정에 기초한다.

후속 모델

차량 추종 모델은 한 차량이 중단 없는 교통 흐름에서 어떻게 다른 차량을 따라가는지를 설명합니다.그것들은 미시적인 교통 흐름 모델의 한 종류입니다.

자동차 후속 모델의 예

뉴웰의 자동차 추종 모델
루이 A.파이프는 1950년대 초에 연구를 시작했고 대중들로부터 인정을 받기 시작했다.파이프 차량 추종 모델은 캘리포니아 자동차 코드의 안전 주행 규칙을 기반으로 하며, 이 모델은 안전 거리를 가정한 것입니다. 다른 차량을 추종하기 위한 좋은 규칙은 차량 속도의 시간당 10마일마다 차량 길이의 최소 차간 거리를 할당하는 것입니다.m
차량 추종의 역학에서 잠재적 비선형 효과를 포착하기 위해, G. F.뉴웰은 경험적 데이터에 기초한 비선형 자동차 추종^[36] 모델을 제안했다.안전 운전 규칙에만 의존하는 파이프 모델과 달리 Newell 비선형 모델은 기본 다이어그램의 올바른 모양(예: 밀도-속도, 유속, 밀도-흐름, 간격-속도, 속도-진행 등)을 포착하는 것을 목표로 합니다.
최적 속도 모델(OVM)은 각 운전자가 앞선 차량 간의 차간 차이와 속도 차이에 따라 최적의 속도에 도달하려고 한다는 가정에 기초하여 1995년에 반도 등에 의해 도입되었다.
지능형 운전자 모델은 연결 차량(CV) 및 연결 및 자율 주행 차량(CAV) 연구에 널리 채택되고 있습니다.

「」를 참조해 주세요.

레퍼런스

^ Henry Lieu (January–February 1999). "Traffic-Flow Theory". Public Roads (Vol. 62· No. 4).
^ Rijn, John (2004). "Road Capacities" (PDF). Indevelopment. Archived from the original (PDF) on 10 January 2017. Retrieved 22 July 2014.
^ V.L. Knoop and W. Daamen (2017). "Automatic fitting procedure for the fundamental diagram". Transportmetrica B: Transport Dynamics. 5 (2): 133–148. doi:10.1080/21680566.2016.1256239.
^ Lint, J. W. C. V., "고속도로의 신뢰성 높은 이동시간 예측", 박사논문, 네덜란드 TRAIL Research School, 2004
^ 고속도로 용량 매뉴얼 2000
^ 새턴 ITS 트랜스포트 소프트웨어 사이트
^ 콘트램의 개요
^ 영국 교통부 WebTag의 운송 연구 수행 지침
^ Cassidy, M.J.; Bertini, R.L. (1999). "Some Traffic Features at Freeway Bottlenecks". Transportation Research Part B: Methodological. 33 (1): 25–42. doi:10.1016/S0191-2615(98)00023-X.
^ ^a ^b Pitstick, Mark E. "누적 곡선을 사용하여 격리된 신호 교차로에서 지연 측정 및 성능 시뮬레이션"교통연구기록 1287(1990)
^ 후안 카를로스 무뇨스와 호르헤 A.Laval. "혼잡한 고속도로와 하나의 목적지에 대한 시스템 최적 동적 트래픽 할당 그래픽 솔루션 방법"교통연구부: 방법론 (2006)
^ ^a ^b Xu, Wang (2016). "Implementation of Variable Speed Limits: Preliminary Test on Whitemud Drive, Edmonton, Canada". Journal of Transportation Engineering. 142 (12): 05016007. doi:10.1061/(ASCE)TE.1943-5436.0000895.
^ Texas A&M Transportation Institute. "Variable Speed Limits" (PDF). Traffic Management. Texas A&M. Retrieved 2018-12-03.
^ Mahmud, Khizir; Town, Graham E. (June 2016). "A review of computer tools for modeling electric vehicle energy requirements and their impact on power distribution networks". Applied Energy. 172: 337–359. doi:10.1016/j.apenergy.2016.03.100.
^ ^a ^b ^c ^d ^e Lighthill, M.J.; Whitham, G.B. (1955). "On kinematic waves. I: Flood movement in long rivers. II: A theory of traffic flow on long crowded roads". Proceedings of the Royal Society. 229A (4): 281–345.
^ P.I. 리차드 "고속도로 충격파"운용방법, 4, 42-51(1956)
^ Daganzo, Carlos F. (1994). "The cell transmission model: A dynamic representation of highway traffic consistent with the hydrodynamic theory". Transportation Research Part B: Methodological. 28 (4): 269–287. doi:10.1016/0191-2615(94)90002-7.
^ R. Herman, E.W. Montroll, R.B. Potts 및 R.W. Rothery, "교통 역학: 자동차 추종 시 안정성 분석"조작, Res., 7, 86-106(1959)
^ D.C. 가지스, R.허먼, 그리고 R.W. 로터리."트래픽 흐름의 비선형 추종 모델"운영 체제, 9, 545-567(1961)
^ Kerner, Boris S. (2013). "Criticism of generally accepted fundamentals and methodologies of traffic and transportation theory: A brief review". Physica A: Statistical Mechanics and Its Applications. 392 (21): 5261–5282. Bibcode:2013PhyA..392.5261K. doi:10.1016/j.physa.2013.06.004.
^ 그린실드, B.D. "교통용량 연구"도로조사위원회 절차, 14, 448~477(1935)
^ Elefteriadou, L. "교통 흐름 이론 입문"Springer Optimization and Is Applications, Vol. 84(스프링거, 2014년 베를린)
^ J.G. Wardrop, "도로 교통 연구의 이론적인 측면들"은 Civil Eng.의 Proc.에 있습니다.II., 1,325 - 362 (1952)
^ Boris S. Kerner, "트래픽 흐름에서의 자기조직의 실험적 특성" 물리 리뷰 레터 81, 3797-3800(1998).doi: 10.1103/PhysRevLett.81.3797
^ Boris S. Kerner, "Congested Traffic Flow: Observations and Theory" 교통 연구 기록, 1678, 160-167(1999)doi: 10.3141/1678-20
^ 보리스 S. 케너, "교통의 물리학" 물리학 세계 12, No.8, 25-30(1999년 8월).doi: 10.1088/2058-7058/12/8/30
^ Boris S. Kerner, The Physical of Traffic: 경험적 고속도로 패턴 특성, 엔지니어링 응용 및 이론, 스프링거, 베를린, 하이델베르크, 뉴욕 2004
^ Boris S. Kerner, 현대 교통 흐름 이론 및 제어 개요: 3상 교통이론의 긴 길, 스프링거, 하이델버그, 도드레흐트, 런던, 뉴욕, 2009
^ Boris S. Kerner, 트래픽네트워크의 개요: 교통과학의 기초, 스프링거, 베를린, 2017
^ Boris S. Kerner, 실제 교통의 이해: 교통과학의 패러다임 변화, 스프링거, 베를린, 하이델베르크, 뉴욕 2021
^ Hubert Rehborn, Micha Koller, Stefan Kaufmann, 데이터 기반 트래픽 엔지니어링: 3상 교통이론에 기초한 교통과 응용에 관한 이해, 암스테르담, 엘세비어, 2020
^ Newell, Gordon (1982). Applications of Queueing Theory (2nd ed.). London: Chapman and Hall.
^ Daganzo, Carlos (1994). "The Cell Transmission Model, part II: Network Traffic". Transportation Research Part B: Methodological. 28 (2): 279–293.
^ Cassidy, Michael J.; Ahn, Soyoung (2005). "Driver Turn-Taking Behavior in Congested Freeway Merges" (PDF). Transportation Research Record: Journal of the Transportation Research Board. 1934: 140–147. CiteSeerX 10.1.1.367.2080. doi:10.3141/1934-15.
^ Pipes, Louis A. (1953). "An Operational Analysis of Traffic Dynamics". Journal of Applied Physics. 24 (3): 274–281. Bibcode:1953JAP....24..274P. doi:10.1063/1.1721265.
^ Newell, G. F. (1961). "Nonlinear Effects in the Dynamics of Car Following". Operations Research. 9 (2): 209–229. doi:10.1287/opre.9.2.209. JSTOR 167493.
^ Bando, M.; Hasebe, K.; Nakayama, A.; Shibata, A.; Sugiyama, Y. (1995). "Dynamical model of traffic congestion and numerical simulation". Physical Review E. 51 (2): 1035–1042. Bibcode:1995PhRvE..51.1035B. doi:10.1103/PhysRevE.51.1035. PMID 9962746.

추가 정보

트래픽 흐름 모델링의 최신 기술에 대한 조사:

N. Bellomo, V. Coscia, M. Delitala, 차량 교통 흐름의 수학적 이론에 대하여 I.유체 역학 및 운동 모델링, 수학. 모드, 메트 신청서 제12권 제12호(2002) 1801~1843호
S. Maerivoet, 자동차 도로에서의 교통 모델링: Katholike Universityit Leuven, 2006년, 최첨단 수치 데이터 분석 및 동적 트래픽 할당
M. Garabello와 B.Piccoli, 네트워크상의 트래픽플로우, 미국수학과학연구소(AIM), 스프링필드, MO, 2006. 페이지 16+243 ISBN 978-1-60133-000-0
카를로스 F.Daganzo, "수송 및 교통 운영의 기초", 영국 옥스퍼드주 Pergamon-Elsevier(1997년)
B.S. Kerner, 최신 트래픽흐름 이론 및 제어 개요: 뉴욕, 베를린, 스프링거, 3상 교통 이론으로의 긴 길 2009
캐시디, M.J., R.L. 베르티니."고속도로 병목현장에서 관측"교통과 교통 이론(1999년).
Daganzo, Carlos F. "간단한 교통 분석 절차"Networks and Space Economics 1.i (2001) : 77 ~101.
Lindgren, Roger V.F. "독일 고속도로 대기 교통 흐름 특성 분석"포틀랜드 주립 대학교(2005년).
니, B, J.D.레너드."트래픽 스트림 특성을 정의하는 직접적인 방법"교통 연구 기록(2006년).

물리적 관점에서 유용한 책:

M. Treiber와 A.Kesting, "Traffic Flow Dynamics", Springer, 2013
B.S. Kerner, The Physical of Traffic, Springer, Berlin, New York 2004
arxiv.org 상의 트래픽플로우
메이, 아돌프트래픽 흐름의 기초프린티스 홀, 뉴저지 주, 잉글우드 절벽, 1990년
테일러, 니콜라스Contram 다이내믹트래픽 할당 모델 TRL 2003

외부 링크

교통연구위원회(TRB) 고속도로 용량 매뉴얼(HCM 2010) 제5판

[1] Henry Lieu (January–February 1999). "Traffic-Flow Theory". Public Roads (Vol. 62· No. 4).

[2] Rijn, John (2004). "Road Capacities" (PDF). Indevelopment. Archived from the original (PDF) on 10 January 2017. Retrieved 22 July 2014.

[3] V.L. Knoop and W. Daamen (2017). "Automatic fitting procedure for the fundamental diagram". Transportmetrica B: Transport Dynamics. 5 (2): 133–148. doi:10.1080/21680566.2016.1256239.

[4] Lint, J. W. C. V., "고속도로의 신뢰성 높은 이동시간 예측", 박사논문, 네덜란드 TRAIL Research School, 2004

[5] 고속도로 용량 매뉴얼 2000

[6] 새턴 ITS 트랜스포트 소프트웨어 사이트

[7] 콘트램의 개요

[8] 영국 교통부 WebTag의 운송 연구 수행 지침

[9] Cassidy, M.J.; Bertini, R.L. (1999). "Some Traffic Features at Freeway Bottlenecks". Transportation Research Part B: Methodological. 33 (1): 25–42. doi:10.1016/S0191-2615(98)00023-X.

[Pitstick-10] Pitstick, Mark E. "누적 곡선을 사용하여 격리된 신호 교차로에서 지연 측정 및 성능 시뮬레이션"교통연구기록 1287(1990)

[11] 후안 카를로스 무뇨스와 호르헤 A.Laval. "혼잡한 고속도로와 하나의 목적지에 대한 시스템 최적 동적 트래픽 할당 그래픽 솔루션 방법"교통연구부: 방법론 (2006)

[ReferenceA-12] Xu, Wang (2016). "Implementation of Variable Speed Limits: Preliminary Test on Whitemud Drive, Edmonton, Canada". Journal of Transportation Engineering. 142 (12): 05016007. doi:10.1061/(ASCE)TE.1943-5436.0000895.

[13] Texas A&M Transportation Institute. "Variable Speed Limits" (PDF). Traffic Management. Texas A&M. Retrieved 2018-12-03.

[14] Mahmud, Khizir; Town, Graham E. (June 2016). "A review of computer tools for modeling electric vehicle energy requirements and their impact on power distribution networks". Applied Energy. 172: 337–359. doi:10.1016/j.apenergy.2016.03.100.

[lighthill_whitham_1955-15] Lighthill, M.J.; Whitham, G.B. (1955). "On kinematic waves. I: Flood movement in long rivers. II: A theory of traffic flow on long crowded roads". Proceedings of the Royal Society. 229A (4): 281–345.

[RichardsLWR-16] P.I. 리차드 "고속도로 충격파"운용방법, 4, 42-51(1956)

[Daganzo_CTM-17] Daganzo, Carlos F. (1994). "The cell transmission model: A dynamic representation of highway traffic consistent with the hydrodynamic theory". Transportation Research Part B: Methodological. 28 (4): 269–287. doi:10.1016/0191-2615(94)90002-7.

[GM1-18] R. Herman, E.W. Montroll, R.B. Potts 및 R.W. Rothery, "교통 역학: 자동차 추종 시 안정성 분석"조작, Res., 7, 86-106(1959)

[GM2-19] D.C. 가지스, R.허먼, 그리고 R.W. 로터리."트래픽 흐름의 비선형 추종 모델"운영 체제, 9, 545-567(1961)

[KernerReview-20] Kerner, Boris S. (2013). "Criticism of generally accepted fundamentals and methodologies of traffic and transportation theory: A brief review". Physica A: Statistical Mechanics and Its Applications. 392 (21): 5261–5282. Bibcode:2013PhyA..392.5261K. doi:10.1016/j.physa.2013.06.004.

[Greenshields-21] 그린실드, B.D. "교통용량 연구"도로조사위원회 절차, 14, 448~477(1935)

[Elefteriadou-22] Elefteriadou, L. "교통 흐름 이론 입문"Springer Optimization and Is Applications, Vol. 84(스프링거, 2014년 베를린)

[Wardrop-23] J.G. Wardrop, "도로 교통 연구의 이론적인 측면들"은 Civil Eng.의 Proc.에 있습니다.II., 1,325 - 362 (1952)

[KernerP1998A-24] Boris S. Kerner, "트래픽 흐름에서의 자기조직의 실험적 특성" 물리 리뷰 레터 81, 3797-3800(1998).doi: 10.1103/PhysRevLett.81.3797

[KernerP1999A-25] Boris S. Kerner, "Congested Traffic Flow: Observations and Theory" 교통 연구 기록, 1678, 160-167(1999)doi: 10.3141/1678-20

[KernerP1999B-26] 보리스 S. 케너, "교통의 물리학" 물리학 세계 12, No.8, 25-30(1999년 8월).doi: 10.1088/2058-7058/12/8/30

[KernerB2004-27] Boris S. Kerner, The Physical of Traffic: 경험적 고속도로 패턴 특성, 엔지니어링 응용 및 이론, 스프링거, 베를린, 하이델베르크, 뉴욕 2004

[KernerB2009-28] Boris S. Kerner, 현대 교통 흐름 이론 및 제어 개요: 3상 교통이론의 긴 길, 스프링거, 하이델버그, 도드레흐트, 런던, 뉴욕, 2009

[KernerB2017-29] Boris S. Kerner, 트래픽네트워크의 개요: 교통과학의 기초, 스프링거, 베를린, 2017

[KernerB2021-30] Boris S. Kerner, 실제 교통의 이해: 교통과학의 패러다임 변화, 스프링거, 베를린, 하이델베르크, 뉴욕 2021

[RehbornBook-31] Hubert Rehborn, Micha Koller, Stefan Kaufmann, 데이터 기반 트래픽 엔지니어링: 3상 교통이론에 기초한 교통과 응용에 관한 이해, 암스테르담, 엘세비어, 2020

[32] Newell, Gordon (1982). Applications of Queueing Theory (2nd ed.). London: Chapman and Hall.

[33] Daganzo, Carlos (1994). "The Cell Transmission Model, part II: Network Traffic". Transportation Research Part B: Methodological. 28 (2): 279–293.

[34] Cassidy, Michael J.; Ahn, Soyoung (2005). "Driver Turn-Taking Behavior in Congested Freeway Merges" (PDF). Transportation Research Record: Journal of the Transportation Research Board. 1934: 140–147. CiteSeerX 10.1.1.367.2080. doi:10.3141/1934-15.

[35] Pipes, Louis A. (1953). "An Operational Analysis of Traffic Dynamics". Journal of Applied Physics. 24 (3): 274–281. Bibcode:1953JAP....24..274P. doi:10.1063/1.1721265.

[36] Newell, G. F. (1961). "Nonlinear Effects in the Dynamics of Car Following". Operations Research. 9 (2): 209–229. doi:10.1287/opre.9.2.209. JSTOR 167493.

[37] Bando, M.; Hasebe, K.; Nakayama, A.; Shibata, A.; Sugiyama, Y. (1995). "Dynamical model of traffic congestion and numerical simulation". Physical Review E. 51 (2): 1035–1042. Bibcode:1995PhRvE..51.1035B. doi:10.1103/PhysRevE.51.1035. PMID 9962746.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[36]

Search

트래픽 플로우

네임스페이스

더

목차

역사

개요

트래픽 스트림 속성

스피드

밀도

흐름

분석 방법