TLA+

TLA+ 툴박스
	TLA+ IDE는 일반적으로 왼쪽의 사양 탐색기, 가운데의 편집기, 오른쪽의 구문 분석 오류를 보여 준다.
원본 작성자	시몬 잠브로프스키, 마르쿠스 쿠페, 다니엘 리케츠
개발자	휴렛패커드, 마이크로소프트
초기 릴리즈	2010년 2월 4일; 12년 전
안정적 해제	1.7.0 / 2020년 4월 25일; 22개월 전
릴리스 미리 보기	1.7.1 / 2020년 5월 1일; 22개월 전
리포지토리	github.com/tlaplus/tlaplus
기록 위치	자바
다음에서 사용 가능	영어
유형	통합 개발 환경
면허증	MIT 라이선스
웹사이트	research.microsoft.com/en-us/um/people/lamport/tla/toolbox.html

패러다임	액션
설계자	레슬리 램포트
첫 등장	1999년 4월 23일; 22년 전
안정적 해제	TLA+2 / 2014년 1월 15일; 8년 전
구현 언어	자바
OS	크로스 플랫폼(멀티 플랫폼)
면허증	MIT 라이선스
파일 이름 확장명	.tla
웹사이트	lamport.azurewebsites.net/tla/tla.html

TLA⁺

TLA는⁺ 레슬리 램포트가 개발한 정식 사양 언어다.프로그램, 특히 동시 시스템과 분산 시스템을 설계, 모델링, 문서화 및 검증하는 데 사용된다.TLA는⁺ 철저한 검증이 가능한 유사 코드로서 소프트웨어 시스템의 ^[4]청사진을 그리는 것에 비유된다.^[5] TLA는 시간적 행동 논리(Temporary Logic of Actions)의 약자다.

설계 및 문서화의 경우 TLA는⁺ 비공식적인 기술 사양과 동일한 목적을 달성한다.단, TLA⁺ 규격은 로직과 수학의 공식 언어로 작성되며, 이 언어로 작성된 규격의 정밀도는 시스템 구현이 진행되기 전에 설계 결함을 밝혀내기 위한 것이다.^[6]

TLA⁺ 사양은 공식 언어로 작성되기 때문에 유한 모델 확인에 적합하다.모델 체커는 가능한 모든 시스템 동작을 일부 실행 단계까지 찾아 안전 및 활성과 같은 원하는 비협조 속성의 위반 여부를 검사한다.TLA⁺ 규격은 안전(나쁜 일은 일어나지 않을 것)을 정의하기 위해 기본 세트 이론을 사용하고, 활성(좋은 일은 결국 일어난다)을 정의하기 위해 시간적 논리를 사용한다.

TLA는⁺ 또한 알고리즘과 수학적 이론 모두를 위해 기계 검사로 정확성을 증명하는 증거를 작성하는 데 사용된다.증명서는 어떤 하나의 정리 백엔드와는 무관하게 선언적이고 위계적인 문체로 쓰여진다.공식 및 비공식 구조 수학적 증명서는 모두 TLA로⁺ 작성할 수 있다. 언어는 LaTeX와 유사하며, TLA⁺ 사양을 LaTeX 문서로 변환할 수 있는 도구가 존재한다.^[7]

TLA는⁺ 동시 시스템 검증 방법에 대한 수십 년의 연구 끝에 1999년에 도입되었다.IDE와 분산형 모델 체커를 포함한 툴체인이 그 이후 개발되었다.PluxCal은 2009년에 만들어졌으며, TLA로⁺ 옮겨지며 순차 알고리즘을 지정하는 데 유용하다.TLA는⁺² 2014년 발표돼 교정구조에 대한 언어지원이 확대됐다.현재 TLA⁺ 참조는 레슬리 램포트의 TLA⁺ 하이퍼북이다.

역사

Amir Pnueli는 컴퓨터 과학에 시간적 논리를 적용했고, 그는 1996년 튜링 상을 받았다.

현대의 시간적 논리는 1957년 아서 프라이어에 의해 개발되었고, 그 후 긴장 논리라고 불렸다.비록 Amir Pnueli가 컴퓨터 과학에 대한 시간적 논리학의 적용을 진지하게 연구한 최초의 사람이었지만, Preter는 10년 전인 1967년에 그것의 사용에 대해 추측했다.

이러한 종류의 [별도의 시간에] 시스템의 유용성은 시간이 불연속적이라는 어떤 심각한 형이상학적 가정에 의존하지 않는다. 그것들은 디지털 컴퓨터의 작업과 같은 일련의 이산상태에서 다음에 일어날 일에만 우리가 관심을 갖는 제한된 담화 분야에만 적용된다.

Pnueli는 1977년 선형 시간 논리를 도입하면서 컴퓨터 프로그램에 대한 명시와 추론에서 시간 논리학의 사용을 연구했다.LTL은 상호 배제, 교착상태로부터의 자유 등의 속성을 쉽게 표현하면서 동시 프로그램 분석을 위한 중요한 도구가 되었다.^[8]

Pnueli의 LTL 연구와 동시에, 학자들은 다중 처리 프로그램 검증을 위한 Hoare 논리를 일반화하기 위해 노력하고 있었다.Leslie Lamport는 동료 검토가 상호 배제에 대해 제출한 논문에서 오류를 발견한 후 이 문제에 관심을 갖게 되었다.에드 애쉬크로프트는 1975년 논문 "병렬 프로그램에 대한 프로빙 어워드"에서 램포트가 1977년 논문 "다중처리 프로그램의 프로빙 정확성"에서 플로이드의 방법을 일반화하는데 사용한 비협조성을 소개했다.램포트 논문은 안전성과 적극성을 각각 부분적 정확성과 종료의 일반화로서 소개했다.^[9]이 방법은 1978년 Edsger Dijkstra와 함께 논문에서 최초의 동시 쓰레기 수거 알고리즘을 검증하는 데 사용되었다.^[10]

램포트는 수잔 오위키에 의해 조직된 1978년 스탠포드 대학 세미나에서 페누엘리의 LTL을 처음 접했다.램포트에 따르면 "일시적 논리는 결코 실용적이지 못할 추상적인 허튼소리라고 확신했지만 재미있어 보여 참석하게 됐다"고 말했다.1980년에 그는 "Somesime is Tomes are Sometimes 'Not Never'"를 발표했는데, 이 논문은 시간 논리학 문헌에서 가장 자주 인용되는 논문 중 하나가 되었다.^[11]램포트는 SRI에 근무하던 시절 시간적 논리 규격 작성에 힘썼으나 이 접근법이 비현실적이라는 것을 알았다.

TLA는⁺ 컴퓨터 과학자와 2013 튜링상 수상자인 레슬리 램포트에 의해 개발되었다.

그러나 슈워츠, 멜리아-스미스, 프리츠 보그트가 간단한 FIFO 대기열을 특정하기 위해 며칠을 허비하고 있는 것을 보고 시간적 논리에 환멸을 느꼈다.나는 그것의 미적 매력에도 불구하고 시간적 특성의 결합으로서 명세서를 쓰는 것은 실제로 효과가 없다는 것을 깨달았다.^[12]

그가 실용적인 사양 방법을 모색한 결과 1983년 논문 "동시 프로그래밍 모듈 지정"이 나왔고, 이 논문은 상태 전환을 원시 변수와 비주요 변수의 부울 값 함수로 기술하는 아이디어를 소개했다.^[12]1980년대 내내 작업이 이어졌고, 램포트는 1990년부터 행동의 시간적 논리에 관한 논문을 발표하기 시작했지만, 1994년 <시간적 행동 논리>가 출간되기 전까지는 정식으로 소개되지 않았다.TLA는 시간적 공식에서의 조치의 사용을 가능하게 했는데, Lamport에 따르면 "동시 시스템 검증에 사용되는 모든 추론을 공식화하고 체계화하는 우아한 방법을 제공한다"^[13]고 한다.

TLA 규격은 대부분 일반적인 비임시 수학으로 구성되었는데, 램포트는 순전히 일시적 규격보다 덜 번거롭다고 생각했다.TLA는 1999년에 "TLA로⁺ 동시 시스템 지정"이라는 논문과 함께 도입된 규격 언어 TLA에⁺ 수학적 기초를 제공했다.^[1]같은 해 말, 위안유는 TLA⁺ 규격에 대한 TLC 모델 체커를 작성했고, TLC는 Compaq 멀티프로세서의 캐시 일관성 프로토콜에서 오류를 찾는 데 사용되었다.^[14]

램포트는 2002년 TLA에⁺ 관한 전문 교과서를 출간했다.소프트웨어 엔지니어를 위한 TLA⁺ 언어 및 도구".^[15]PlusCal은 2009년에,^[16] TLA⁺ 인증 시스템은 2012년에 도입되었다.^[17]TLA는⁺² 2014년에 발표되었으며, 입증 시스템에 대한 언어 내 지원을 크게 증가시킬 뿐만 아니라 일부 추가 언어 구조를 추가했다.^[2]Lamport는 업데이트된⁺ TLA 참조 자료인 "TLA⁺ 하이퍼북"을 만드는 작업에 참여하고 있다.그 불완전한 작품은 그의 공식 웹사이트에서 볼 수 있다.램포트는 또한 거기서 "프로그래머와 소프트웨어 엔지니어에게 그들만의 TLA+ 스펙을 작성하는 방법을 가르치는 일련의 비디오 강의의 시작으로 구성된 진행 중인 작품"이라고 기술한 The TLA+ 비디오 코스를 만들고 있다.

언어

TLA⁺ 사양을 모듈로 정리한다.모듈은 기능을 사용하기 위해 다른 모듈을 확장(가져오기)할 수 있다.TLA⁺ 표준은 형식 수학적 기호에 명시되어 있지만, 기존 TLA⁺ 도구는 ASCII에서 LaTeX와 같은 기호 정의를 사용한다.TLA는⁺ 정의가 필요한 몇 가지 용어를 사용한다.

상태 – 변수에 대한 값 할당
행동 – 일련의 상태
단계 – 동작에서 한 쌍의 연속 상태
더듬는 단계 – 변수가 변경되지 않는 단계
차상위 관계 – 모든 단계에서 변수가 어떻게 변할 수 있는지 설명하는 관계
상태 함수 – 다음 상태 관계가 아닌 변수 및 상수를 포함하는 식
상태 술어 – 부울 값 상태 함수
불변성 – 도달 가능한 모든 상태에서 참인 상태 술어
시간 공식 - 시간 논리학에서 문구를 포함하는 표현

안전

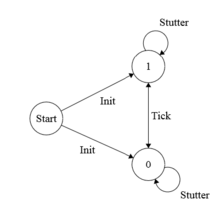
TLA는⁺ 모든 올바른 시스템 행동의 집합을 정의하는 것과 관련이 있다.예를 들어 0과 1 사이에 끝없이 똑딱거리는 1비트 시계는 다음과 같이 지정할 수 있다.

Variable clock Init == 시계 \in {0, 1} 체크 표시 == IF 클럭 = 0이면 시계 = 1 EAST 시계' = 0 Spec == Init /\[][Tick]_<clock>

다음 상태 관계 체크 표시는 클럭을 0이면 1로, 클럭이 1이면 0으로 설정한다.시계의 값이 0 또는 1이면 상태 조건인 Init가 참이다.Spec은 1비트 시계의 모든 동작이 초기에는 Init를 만족시켜야 하며 모든 스텝이 Chick과 일치하거나 더듬거리는 스텝을 가져야 한다는 시간적 공식이다.그러한 행동 두 가지는 다음과 같다.

0 -> 1 -> 0 -> 1 -> 0 -> ...  1 -> 0 -> 1 -> 0 -> 1 -> ...

1비트 클럭(접근 가능한 시스템 상태 집합)의 안전 속성은 규격에 의해 적절히 설명된다.

리브

위의 사양은 1비트 시계에 대해 이상한 상태를 허용하지 않지만 시계가 절대 똑딱거릴 것이라고는 말하지 않는다.예를 들어, 다음과 같은 영구적인 행동이 허용된다.

0 -> 0 -> 0 -> 0 -> 0 -> ...  1 -> 1 -> 1 -> 1 -> 1 -> ...

시계가 똑딱거리지 않는 것은 유용하지 않기 때문에 이러한 행동은 허용되지 않아야 한다.한 가지 해결책은 말더듬이를 비활성화하는 것이지만 TLA는⁺ 항상 말더듬이를 활성화해야 한다. 말더듬는 단계는 규격에 설명되지 않은 시스템의 일부에 대한 변경을 의미하며, 정교화에 유용하다.시계가 결국 체크 표시를 해야 한다는 것을 보장하기 위해 체크 표시에 대해 약한 공정성이 주장된다.

사양 == Init /\[Tick]_<<clock> /\ WF_<clock>(Tick)

행동에 대한 약한 공정성은 그 행동이 지속적으로 활성화된다면, 결국 실행되어야 한다는 것을 의미한다.틱에 대한 공정성이 약하기 때문에 틱 사이에 제한된 수의 더듬는 단계만 허용된다.틱에 대한 이 시간적 논리적인 진술은 lavity adjust라고 불린다.일반적으로, 연성 주장은 기계적으로 폐쇄되어야 한다: 그것은 도달 가능한 상태의 집합에 제약을 가해서는 안 되며, 가능한 행동의 집합만을 구속해서는 안 된다.^[18]

대부분의 규격은 연성 특성을 주장할 필요가 없다.안전 속성은 모델 점검과 시스템 구현 지침 모두에 충분하다.^[19]

연산자

TLA는⁺ ZF를 기반으로 하기 때문에 변수에 대한 연산은 세트 조작을 포함한다.언어는 집합 멤버쉽, 조합, 교차로, 차이, 파워셋 및 하위 집합 연산자를 포함한다. $\lor,$ ∧, ↔,↔,↔, $\leftrightarrow$ 등의 1차 논리 연산자도 포함되며, 보편적, 실존적 정량자 quant $,$ ∃도 포함된다 $.$ Hilbert의 $ε$ 은 임의의 세트 요소를 고유하게 선택하는 SELECT 연산자로 제공된다.리얼, 정수, 자연수 이상의 산술 연산자는 표준 모듈에서 구할 수 있다.

시간 논리 연산자는 TLA에⁺ 내장되어 있다. $\Box P$ 공식은 ${$ P {\ $displaystyle \Box P}$ 을 $\Box P$ (를) 사용하여 P가 항상 참임을 의미하며, $\Diamond P$ $\Diamond P$ $\Diamond P$ 은 $\Diamond P$ 결국 참임을 의미한다.연산자는 P가 무한히 자주 참임을 의미하기 위해 $\Box \Diamond P$ $\Box \Diamond P$ { $\Box \Diamond P$ P {\ $displaystyle \Diamond P}$ 로 결합되고, $\Diamond \Box P$ $\Diamond \Box P$ $\Diamond \Box P$ $\Diamond \Box P$ 는 $\Diamond \Box P$ 결국 P가 항상 참임을 의미한다.다른 시간적 운영자들은 약하고 강한 공정성을 포함한다.약한 공정성 WF_e(A)는 조치 A가 지속적으로 활성화된 경우(즉, 중단 없이) 결국 실행되어야 함을 의미한다.강력한 공정성 SF_e(A)는 A 조치가 지속적으로 활성화되면(반복적으로, 중단 여부와 상관없이), 결국 실행되어야 한다는 것을 의미한다.

TLA에는⁺ 도구의 지원이 없더라도 시간적 실존적 및 보편적 정량화가 포함된다.

사용자 정의 연산자는 매크로와 유사하다.연산자는 자신의 도메인이 세트가 될 필요가 없다는 점에서 기능과는 다르다. 예를 들어, 세트 멤버십 연산자는 세트의 범주를 그 도메인으로 가지고 있는데, 이것은 ZFC에서 유효한 세트가 아니다(그 존재는 러셀의 역설로 이어지기 때문에).재귀적이고 익명의 사용자 정의 연산자가 TLA에⁺² 추가되었다.

데이터 구조

TLA의⁺ 기초 데이터 구조는 세트다.세트는 명시적으로 열거되거나 연산자를 사용하여 다른 세트에서 생성되거나{x \in S : p}여기서 p는 x에 어떤 조건이다.{e : x \in S}여기서 e는 x의 어떤 기능이다.고유한 빈 집합은 다음과 같이 표현된다.{}.

TLA의⁺ 함수는 도메인의 각 요소, 집합에 값을 할당한다. [S -> T]도메인 집합 S의 각 x에 대해, T에 f[x]가 있는 모든 함수의 집합이다.예를 들어, TLA⁺ 함수Double[x \in Nat] == x*2세트 구성 요소[Nat -> Nat]그렇게Double \in [Nat -> Nat]TLA의⁺ 진실된 진술이야함수는 또한 다음 항목으로 정의된다.[x \in S -> e]일부 표현식 e 또는 기존 함수를 수정하여[f EXCEPT ![v₁] = v₂].

레코드는 TLA에서⁺ 기능의 일종이다.레코드[name -> "John", age -> 35]필드 이름 및 연령이 있는 레코드로 액세스 가능r.name그리고r.age, 그리고 레코드 세트에 소속되어 있다.[name : String, age : Nat].

TLA에는⁺ 튜플이 포함되어 있다.그들은 명시적으로 다음과 같이 정의되어 있다.<<e₁,e₂,e₃>>또는 표준 시퀀스 모듈의 연산자로 구성된다.튜플 집합은 데카르트 제품으로 정의된다. 예를 들어, 모든 자연수 쌍의 집합은 정의된다.Nat \X Nat.

표준 모듈

TLA에는⁺ 공통 연산자가 포함된 표준 모듈 세트가 있다.그것들은 구문 분석기와 함께 분포한다.TLC 모델 체커는 성능 향상을 위해 Java 구현을 사용한다.

유한 세트: 유한 세트 작업용 모듈.IsFiniteSet(S) 및 Cardinality(S) 연산자 제공
시퀀스:Len(S), Head(S), Tail(S), Add(S), Connectation(S, E), filter 등의 튜플에 대한 연산자를 정의한다.
가방: 멀티셋 작업용 모듈.원시 세트 작동 아날로그 및 중복 카운트 제공
Naturals:불평등 및 산술 연산자와 함께 자연수를 규정한다.
Integers: Integers를 정의하십시오.
Reals: 분할 및 무한대와 함께 Real number를 정의하십시오.
RealTime: 실시간 시스템 사양에 유용한 정의를 제공한다.
TLC: 로깅 및 주장과 같이 모델 확인 사양을 위한 유틸리티 기능 제공.

표준 모듈은 다음과 함께 가져오기EXTENDS또는INSTANCE진술들

도구들

IDE

Eclipse 위에 통합 개발 환경을 구현한다.여기에는 오류 및 구문 강조 표시가 있는 편집기와 몇 가지 다른 TLA⁺ 도구에 대한 GUI 프런트엔드가 포함된다.

구문 오류를 분석 및 확인하는 SANY 구문 분석기.
LaTeX 번역기, 예쁘게 인쇄된 사양을 만들기 위해.
PlusCal 번역기.
TLC 모델 검사기.
TLAPS 인증 시스템.

IDE는 TLA 도구 상자에 배포된다.

모델체커

TLC가 1비트 클럭에 대해 검색한 상태 및 전환.

TLC 모델 체커는 침입 특성을 확인하기 위해 TLA⁺ 규격의 유한 상태 모델을 구축한다.TLC는 규격을 만족하는 초기 상태 집합을 생성한 다음 정의된 모든 상태 전환에 대해 너비 우선 검색을 수행한다.모든 상태 전환이 이미 발견된 상태로 이어질 때 실행이 중지된다.TLC가 시스템 불변성을 위반하는 상태를 발견하면 중지하고 위반 상태에 대한 상태 추적 경로를 제공한다.TLC는 결합폭발으로부터 방어하기 위해 모델 대칭을 선언하는 방법을 제공한다.^[14]또한 상태 탐색 단계를 병렬화하며, 분산 모드로 실행되어 많은 수의 컴퓨터에 워크로드를 분산시킬 수 있다.^[20]

철저한 범위 우선 검색의 대안으로 TLC는 깊이 우선 검색을 사용하거나 무작위 행동을 발생시킬 수 있다.TLC는 TLA의⁺ 하위 집합에서 작동하며, 모델은 유한하고 열거할 수 있어야 하며, 일부 시간 연산자는 지원하지 않는다.분산 모드에서 TLC는 활성 특성을 검사할 수 없으며 무작위 또는 깊이 우선 행동을 검사할 수 없다.TLC는 명령줄 도구로 사용하거나 TLA 도구 상자와 함께 번들로 제공된다.

증명 시스템

TLA⁺ Proof System 또는 TLAPS는 TLA로⁺ 작성된 증명서를 기계적으로 확인한다.동시 및 분산 알고리즘의 정확성을 증명하기 위해 마이크로소프트 Research-INRIA 공동 센터에서 개발되었다.증명 언어는 어떤 특정한 정리 프로베어링으로부터 독립적이 되도록 설계된다; 증명서는 선언적인 문체로 쓰여지고, 백엔드 지지자들에게 보내지는 개별적인 의무로 변형된다.주요 백엔드 프로바이더는 이사벨과 제논이며, SMT 해결사 CVC3, Yess, Z3로 대체된다.TLAPS 증명서는 계층 구조로 되어 있어 리팩터링을 용이하게 하고 비선형 개발을 가능하게 한다: 모든 이전 단계가 검증되기 전에 이후의 단계에서 작업을 시작할 수 있으며, 어려운 단계는 더 작은 하위 단계로 분해된다.TLAPS는 모델 체커가 확인을 시작하기 전에 작은 오류를 빠르게 발견하기 때문에 TLC와 잘 작동한다.또한, TLAPS는 유한 모델 확인의 기능을 벗어난 시스템 특성을 증명할 수 있다.^[17]

TLAPS는 현재 실수와 대부분의 시간 연산자를 사용한 추론을 지원하지 않는다.이자벨과 제논은 일반적으로 산술 증명 의무를 증명할 수 없어 시만텍 해결사의 사용이 요구된다.^[21]TLAPS는 비잔틴 팍소스의 정확성, 회고록 보안 아키텍처, 페이스트리 분산 해시 테이블의 구성요소,^[17] 스파이어 컨센서스 알고리즘을 입증하기 위해 사용되어 왔다.^[22]나머지 TLA⁺ 도구와 별도로 배포되며 BSD 라이선스에 따라 배포되는 무료 소프트웨어다.^[23]TLA는⁺² 교정 구성에 대한 언어 지원을 대폭 확대했다.

산업용

마이크로소프트에서는 TLA로⁺ 사양을 작성하는 과정에서 Xbox 360 메모리 모듈에서 중요한 버그가 발견되었다.^[24]TLA는⁺ 비잔틴 팍소스와 파스트리 분산 해시 테이블의 구성요소에 대한 정확성에 대한 공식적인 증명서를 작성하는 데 사용되었다.^[17]

아마존웹서비스는 2011년부터 TLA를⁺ 사용해 왔다.DynamoDB, S3, EBS 및 내부 분산형 잠금 관리자에서 발견된 버그를 검사하는 TLA⁺ 모델. 일부 버그는 35단계의 상태 추적이 필요했다.모델 점검은 공격적인 최적화를 검증하는 데도 사용되었다.또한, TLA⁺ 규격은 문서화 및 설계 보조 도구로서 가치가 있는 것으로 밝혀졌다.^[4]^[25]

마이크로소프트 아즈어는 TLA를⁺ 사용하여 5가지 다른 일관성 모델을 가진 전세계적으로 분산된 데이터베이스인 코스모스 DB를 설계했다.^[26]^[27]

Altreonic NV는 OpenCom 모델 확인을 위해 TLA를⁺ 사용했다.RTOS

예

스냅샷 분리가 있는 키 값 저장소

------------------------------------------------------------ 상수   키,            \* 그 세트 의 전부 열쇠들..             발,            \* 그 세트 의 전부 가치.             TxId            \* 그 세트 의 전부 거래 IDs. 변수   저장하다,          \* A 자료 저장하다 맵핑 열쇠들. 로 가치.             tx,             \* 그 세트 의 개방된 스냅 사진을 찍다 거래.             스냅샷저장소,  \* 스냅숏 의 그 저장하다 을 위해 각각 거래.             쓰여진,        \* A 통나무를 하다 의 글씨를 쓰다 수행했다 안쪽에 각각 거래.             놓친          \* 그 세트 의 글씨를 쓰다 보이지 않는 로 각각 거래. ---------------------------------------------------------------------------- 노발 ==    \* 선택하다 무엇인가 로 대표하다 그 결석 의 a 가치를 매기다.     선택 v : v \공증인 발  저장하다 ==    \* 그 세트 의 전부 핵심을-가치를 매기다 상점들.     [키 -> 발 \컵을 {노발}]  초기화 == \* 그 초기의 술어를 붙이다.     /\ 저장하다 = [k \에 키 -> 노발]        \* 전부 저장하다 가치 이다 처음에 노발.     /\ tx = {}                              \* 그 세트 의 개방된 거래 이다 처음에 텅 빈.     /\ 스냅샷저장소 =                      \* 전부 스냅샷저장소 가치 이다 처음에 노발.         [t \에 TxId -> [k \에 키 -> 노발]]     /\ 쓰여진 = [t \에 TxId -> {}]        \* 전부 글씨를 쓰다 통나무 이다 처음에 텅 빈.     /\ 놓친 = [t \에 TxId -> {}]         \* 전부 놓친 글씨를 쓰다 이다 처음에 텅 빈.      타이프인바리안트 ==    \* 그 타자를 치다 불변의.     /\ 저장하다 \에 저장하다     /\ tx \부분집합 TxId     /\ 스냅샷저장소 \에 [TxId -> 저장하다]     /\ 쓰여진 \에 [TxId -> 부분 집합 키]     /\ 놓친 \에 [TxId -> 부분 집합 키]      TxLifecycle ==     /\ \A t \에 tx :    \* 만약 저장하다 != 스냅 사진을 찍다 & 우리 하지 않았다 쓰여진 그럭저럭, 우리 해야 한다 가지고 있다 놓친 a 글씨를 쓰다.         \A k \에 키 : (저장하다[k] /= 스냅샷저장소[t][k] /\ k \공증인 쓰여진[t]) => k \에 놓친[t]     /\ \A t \에 TxId \ tx : \* 수표 거래 이다 청소했다 위로 다음에 처분.         /\ \A k \에 키 : 스냅샷저장소[t][k] = 노발         /\ 쓰여진[t] = {}         /\ 놓친[t] = {}  오픈Tx(t) ==    \* 개방하다 a 새로운 거래.     /\ t \공증인 tx     /\ tx' = tx \컵을 {t}     /\ snapshotStore' = [스냅샷저장소 제외 ![t] = 저장하다]     /\ 변경되지 않음 <<쓰여진, 놓친, 저장하다>>  추가하다(t, k, v) == \* 사용. 거래 t, 덧셈을 가치를 매기다 v 로 그 저장하다 밑에 핵심을 k.     /\ t \에 tx     /\ 스냅샷저장소[t][k] = 노발     /\ snapshotStore' = [스냅샷저장소 제외 ![t][k] = v]     /\ '라고 쓰여진 = [쓰여진 제외 ![t] = @ \컵을 {k}]     /\ 변경되지 않음 <<tx, 놓친, 저장하다>>      갱신하다(t, k, v) ==  \* 사용. 거래 t, 갱신하다 그 가치를 매기다 연관된 와 함께 핵심을 k 로 v.     /\ t \에 tx     /\ 스냅샷저장소[t][k] \공증인 {노발, v}     /\ snapshotStore' = [스냅샷저장소 제외 ![t][k] = v]     /\ '라고 쓰여진 = [쓰여진 제외 ![t] = @ \컵을 {k}]     /\ 변경되지 않음 <<tx, 놓친, 저장하다>>      제거하다(t, k) == \* 사용. 거래 t, 제거하다 핵심을 k 로부터 그 저장하다.     /\ t \에 tx     /\ 스냅샷저장소[t][k] /= 노발     /\ snapshotStore' = [스냅샷저장소 제외 ![t][k] = 노발]     /\ '라고 쓰여진 = [쓰여진 제외 ![t] = @ \컵을 {k}]     /\ 변경되지 않음 <<tx, 놓친, 저장하다>>      롤백Tx(t) ==    \* 가까운. 그 거래 없이 병합 글씨를 쓰다 로 저장하다.     /\ t \에 tx     /\ tx' = tx \ {t}     /\ snapshotStore' = [스냅샷저장소 제외 ![t] = [k \에 키 -> 노발]]     /\ '라고 쓰여진 = [쓰여진 제외 ![t] = {}]     /\ 놓친 = [놓친 제외 ![t] = {}]     /\ 변경되지 않음 저장하다  클로즈Tx(t) ==   \* 가까운. 거래 t, 병합 글씨를 쓰다 로 저장하다.     /\ t \에 tx     /\ 놓친[t] \모자를 씌우다 쓰여진[t] = {}   \* 탐지 의 글씨를 쓰다-글씨를 쓰다 갈등들.     /\ 가게의 =                         \* 병합 스냅샷저장소 글씨를 쓰다 로 저장하다.         [k \에 키 -> IF k \에 쓰여진[t] 그럼 스냅샷저장소[t][k] 기타 저장하다[k]]     /\ tx' = tx \ {t}     /\ 놓친 =    \* 갱신하다 그 놓친 글씨를 쓰다 을 위해 타사의 개방된 거래.         [otherTx \에 TxId -> IF otherTx \에 tx' 그럼 놓친[otherTx] \컵을 쓰여진[t] 기타 {}]     /\ snapshotStore' = [스냅샷저장소 제외 ![t] = [k \에 키 -> 노발]]     /\ '라고 쓰여진 = [쓰여진 제외 ![t] = {}]  다음 == \* 그 다음에-주 관계.     \/ \E t \에 TxId : 오픈Tx(t)     \/ \E t \에 tx : \E k \에 키 : \E v \에 발 : 추가하다(t, k, v)     \/ \E t \에 tx : \E k \에 키 : \E v \에 발 : 갱신하다(t, k, v)     \/ \E t \에 tx : \E k \에 키 : 제거하다(t, k)     \/ \E t \에 tx : 롤백Tx(t)     \/ \E t \에 tx : 클로즈Tx(t)          스펙 == \* 초기화 주 와 함께 초기화 그리고 전이 와 함께 다음.     초기화 /\ [][다음]_<<저장하다, tx, 스냅샷저장소, 쓰여진, 놓친>> ---------------------------------------------------------------------------- 정리 스펙 => [](타이프인바리안트 /\ TxLifecycle) =============================================================================

규칙 기반 방화벽

--------------------------------------------------------------------------------------- 확장     정수 상수   주소,    \* 그 세트 의 전부 주소             항구,       \* 그 세트 의 전부 항구             프로토콜    \* 그 세트 의 전부 프로토콜  어드레스 == \* 그 세트 의 전부 주소를 쓰다 범위     {r \에 주소 \X 주소 : r[1] <= r[2]}  InAddressRange[r \에 어드레스, a \에 주소] ==     /\ r[1] <= a     /\ a <= r[2]  포트레인지 ==    \* 그 세트 의 전부 입항하다 범위     {r \에 항구 \X 항구 : r[1] <= r[2]}  InPortRange[r \에 포트레인지, p \에 항구] ==     /\ r[1] <= p     /\ p <= r[2]  패킷 ==   \* 그 세트 의 전부 꾸러     [sourceAddress : 주소,     소스 포트 : 항구,     destAddress : 주소,     목적지 : 항구,     의정서 : 프로토콜]  방화벽 == \* 그 세트 의 전부 방화벽     [패킷 -> 부울]  규칙 == \* 그 세트 의 전부 방화벽을 치다 규칙.     [remoteAddress : 어드레스,     원격 포트 : 포트레인지,     localAddress : 어드레스,     localPort : 포트레인지,     의정서 : 부분 집합 프로토콜,     허용하다 : 부울]  규칙 집합 ==  \* 그 세트 의 전부 방화벽을 치다 규칙 집합     부분 집합 규칙  허용된[rset \에 규칙 집합, p \에 패킷] ==  \* 여부 그 규칙 집합 허용한다 그 꾸러미를 만들다     LET 성냥 == {통치를 하다 \에 rset :         /\ InAddressRange[통치를 하다.remoteAddress, p.sourceAddress]         /\ InPortRange[통치를 하다.원격 포트, p.소스 포트]         /\ InAddressRange[통치를 하다.localAddress, p.destAddress]         /\ InPortRange[통치를 하다.localPort, p.목적지]         /\ p.의정서 \에 통치를 하다.의정서}     인  /\ 성냥 /= {}         /\ \A 통치를 하다 \에 성냥 : 통치를 하다.허용하다 =============================================================================

멀티카 엘리베이터 시스템

--------------------------------------------------------------------------------------- (***************************************************************************) (* 이것 스펙을 붙이다 설명합니다. a 소박한 다중의-자동차 엘리베이터를 타다 계통. 그 행동들 에  *) (* 이 스펙을 붙이다 이다 천만뜻밖의 그리고 통상의 로 전부 그런 시스템들 빼고는 을 위해    *) (* 디스패치엘레베이터, 어떤 것 포함하다 그 논리학 로 결정하다 어떤 것 엘리베이터를 타다  *) (* 해야 한다 로 서비스 어떤 것 부르다. 그 알고리즘. 사용했다 이다 매우 소박한 그리고 한다 *) (* 아닌 최적화하다 을 위해 전지구적 처리량 또는 평균의 기다리다 시간. 그            *) (* 시간 인바리어트 정의 보증하다 이 사양 제공하다        *) (* 능력 예상한 의 아무 것이나 엘리베이터를 타다 계통, 그런 로서 사람 종국에는 *) (* 도달하는 그들의 목적지 마루를 깔다.                                       *) (***************************************************************************)  확장     정수  상수   사람,     \* 그 세트 의 전부 사람 사용. 그 엘리베이터를 타다 계통             엘리베이터,   \* 그 세트 의 전부 엘리베이터             플로어카운트  \* 그 번호를 붙이다 의 층층 서비스된 에 의해 그 엘리베이터를 타다 계통  변수   퍼스널스테이트,            \* 그 주 의 각각 사람             액티브엘레베이터콜스,    \* 그 세트 의 전부 적극적 엘리베이터를 타다 전화를 하다             엘레베이터스테이트           \* 그 주 의 각각 엘리베이터를 타다  바스 == \* 투플레 의 전부 사양 변수들     <<퍼스널스테이트, 액티브엘레베이터콜스, 엘레베이터스테이트>>  바닥 ==    \* 그 세트 의 전부 층층     1 .. 플로어카운트  방향 ==    \* 방향. 이용할 수 있는 로 이 엘리베이터를 타다 계통     {"업", "다운"}  엘리베이터콜 == \* 그 세트 의 전부 엘리베이터를 타다 전화를 하다     [마루를 깔다 : 바닥, 방향 : 방향]  엘리베이터 방향 상태 ==   \* 엘리베이터 동작 주; 그럭저럭 이다 어느 쪽이든 감동적인 에 a 방향 또는 고정된     방향 \컵을 {"스테이션"}  GetDistance[f1, f2 \에 바닥] ==    \* 그 거리를 두다 사이에 두 개 층층     IF f1 > f2 그럼 f1 - f2 기타 f2 - f1      GetDirection[현재의, 목적지 \에 바닥] == \* 방향 의 여행하다 필수의 로 움직이다 사이에 현재의 그리고 목적지 층층     IF 목적지 > 현재의 그럼 "업" 기타 "다운"  캔서비스콜[e \에 엘리베이터, c \에 엘리베이터콜] ==   \* 여부 엘리베이터를 타다 이다 에 포지션 로 즉시 서비스 부르다     LET eState == 엘레베이터스테이트[e] 인     /\ c.마루를 깔다 = eState.마루를 깔다     /\ c.방향 = eState.방향  피플웨이팅[f \에 바닥, d \에 방향] ==  \* 그 세트 의 전부 사람 기다림 에 관하여 a의 엘리베이터를 타다 부르다     {p \에 사람 :         /\ 퍼스널스테이트[p].위치 = f         /\ 퍼스널스테이트[p].기다림         /\ GetDirection[퍼스널스테이트[p].위치, 퍼스널스테이트[p].목적지] = d}  타이프인바리안트 ==    \* 진술들 에 관하여 그 변수들 어떤 것 우리 기대하다 로 보유하다 에 매사에 계통 주     /\ 퍼스널스테이트 \에 [사람 -> [위치 : 바닥 \컵을 엘리베이터, 목적지 : 바닥, 기다림 : 부울]]     /\ 액티브엘레베이터콜스 \부분집합 엘리베이터콜     /\ 엘레베이터스테이트 \에 [엘리베이터 -> [마루를 깔다 : 바닥, 방향 : 엘리베이터 방향 상태, 문이 열려 있다 : 부울, 단추 누름 : 부분 집합 바닥]]  세이프티인바리안트 ==   \* 일부 더 많은 포괄적 수표 저편에 그 타자를 치다 불변의     /\ \A e \에 엘리베이터 :  \* 안 엘리베이터를 타다 가지다 a 마루를 깔다 단추를 채우다 충분하지 않은 단 한 가지 만일 a 사람 에 저것 엘리베이터를 타다 이다 가는 중 로 저것 마루를 깔다         /\ \A f \에 엘레베이터스테이트[e].단추 누름 :             /\ \E p \에 사람 :                 /\ 퍼스널스테이트[p].위치 = e                 /\ 퍼스널스테이트[p].목적지 = f     /\ \A p \에 사람 :    \* A 사람 이다 에 a의 엘리베이터를 타다 단 한 가지 만일 그 엘리베이터를 타다 이다 감동적인 향하여 그들의 목적지 마루를 깔다         /\ \A e \에 엘리베이터 :             /\ (퍼스널스테이트[p].위치 = e /\ 엘레베이터스테이트[e].마루를 깔다 /= 퍼스널스테이트[p].목적지) =>                  /\ 엘레베이터스테이트[e].방향 = GetDirection[엘레베이터스테이트[e].마루를 깔다, 퍼스널스테이트[p].목적지]     /\ \A c \에 액티브엘레베이터콜스 : 피플웨이팅[c.마루를 깔다, c.방향] /= {} \* 아니요. 귀신이 되다 전화를 하다  시간 인바리어트 ==  \* 기대들 에 관하여 엘리베이터를 타다 계통 능력     /\ \A c \에 엘리베이터콜 :  \* 매 부르다 이다 종국에는 서비스된 에 의해 a의 엘리베이터를 타다         /\ c \에 액티브엘레베이터콜스 ~> \E e \에 엘리베이터 : 캔서비스콜[e, c]     /\ \A p \에 사람 :    \* 만약 a 사람 기다림 을 위해 그들의 엘리베이터를 타다, 그들은 할 것이다. 종국에는 도착하다 에서 그들의 마루를 깔다         /\ 퍼스널스테이트[p].기다림 ~> 퍼스널스테이트[p].위치 = 퍼스널스테이트[p].목적지  픽뉴데스티네이션(p) ==    \* 사람 결정하다 그들은 필요하다 로 가다 로 a 다른 마루를 깔다     LET pState == 퍼스널스테이트[p] 인     /\ ~pState.기다림     /\ pState.위치 \에 바닥     /\ \E f \에 바닥 :         /\ f /= pState.위치         /\ PersonState' = [퍼스널스테이트 제외 ![p] = [@ 제외 !.목적지 = f]]     /\ 변경되지 않음 <<액티브엘레베이터콜스, 엘레베이터스테이트>>  콜엘레베이터(p) ==  \* 사람 전화를 하다 그 엘리베이터를 타다 로 가다 에 a 확실한 방향 로부터 그들의 마루를 깔다     LET pState == 퍼스널스테이트[p] 인     LET 부르다 == [마루를 깔다 -> pState.위치, 방향 -> GetDirection[pState.위치, pState.목적지]] 인     /\ ~pState.기다림     /\ pState.위치 /= pState.목적지     /\ 액티브엘레베이터콜스 =         IF \E e \에 엘리베이터 :             /\ 캔서비스콜[e, 부르다]             /\ 엘레베이터스테이트[e].문이 열려 있다         그럼 액티브엘레베이터콜스         기타 액티브엘레베이터콜스 \컵을 {부르다}     /\ PersonState' = [퍼스널스테이트 제외 ![p] = [@ 제외 !.기다림 = 진실의]]     /\ 변경되지 않음 <<엘레베이터스테이트>>  오픈엘레베이터도어(e) == \* 개방하다 그 엘리베이터를 타다 문들 만일 저기에 이다 a 부르다 에 관하여 이 마루를 깔다 또는 그 단추를 채우다 을 위해 이 마루를 깔다 있었다 충분하지 않은.     LET eState == 엘레베이터스테이트[e] 인     /\ ~eState.문이 열려 있다     /\  \/ \E 부르다 \에 액티브엘레베이터콜스 : 캔서비스콜[e, 부르다]         \/ eState.마루를 깔다 \에 eState.단추 누름     /\ 엘레베이터스테이트' = [엘레베이터스테이트 제외 ![e] = [@ 제외 !.문이 열려 있다 = 진실의, !.단추 누름 = @ \ {eState.마루를 깔다}]]     /\ 액티브엘레베이터콜스 = 액티브엘레베이터콜스 \ {[마루를 깔다 -> eState.마루를 깔다, 방향 -> eState.방향]}     /\ 변경되지 않음 <<퍼스널스테이트>>      EnterElevator(e) == \* 전부 사람 에 관하여 이 마루를 깔다 누구 이다 기다림 을 위해 그 엘리베이터를 타다 그리고 여행하는 그 같은 방향 입장하다 그 엘리베이터를 타다.     LET eState == 엘레베이터스테이트[e] 인     LET 타러 == 피플웨이팅[eState.마루를 깔다, eState.방향] 인     LET 목적지 == {퍼스널스테이트[p].목적지 : p \에 타러} 인     /\ eState.문이 열려 있다     /\ eState.방향 /= "스테이션"     /\ 타러 /= {}     /\ PersonState' = [p \에 사람 ->         IF p \에 타러         그럼 [퍼스널스테이트[p] 제외 !.위치 = e]         기타 퍼스널스테이트[p]]     /\ 엘레베이터스테이트' = [엘레베이터스테이트 제외 ![e] = [@ 제외 !.단추 누름 = @ \컵을 목적지]]     /\ 변경되지 않음 <<액티브엘레베이터콜스>>  엑시트엘레베이터(e) ==  \* 전부 사람 누구의 목적지 이다 이 마루를 깔다 퇴장하다 그 엘리베이터를 타다.     LET eState == 엘레베이터스테이트[e] 인     LET 하차 == {p \에 사람 : 퍼스널스테이트[p].위치 = e /\ 퍼스널스테이트[p].목적지 = eState.마루를 깔다} 인     /\ eState.문이 열려 있다     /\ 하차 /= {}     /\ PersonState' = [p \에 사람 ->         IF p \에 하차         그럼 [퍼스널스테이트[p] 제외 !.위치 = eState.마루를 깔다, !.기다림 = 거짓의]         기타 퍼스널스테이트[p]]     /\ 변경되지 않음 <<액티브엘레베이터콜스, 엘레베이터스테이트>>  클로즈엘레베이터도어(e) ==    \* 가까운. 그 엘리베이터를 타다 문들 한 번 전부 사람 가지고 있다 들어갔다 그리고 나갔다 그 엘리베이터를 타다 에 관하여 이 마루를 깔다.     LET eState == 엘레베이터스테이트[e] 인     /\ ~가능한 EnterElevator(e)     /\ ~가능한 엑시트엘레베이터(e)     /\ eState.문이 열려 있다     /\ 엘레베이터스테이트' = [엘레베이터스테이트 제외 ![e] = [@ 제외 !.문이 열려 있다 = 거짓의]]     /\ 변경되지 않음 <<퍼스널스테이트, 액티브엘레베이터콜스>>  무브엘레베이터(e) ==  \* 이동하다 그 엘리베이터를 타다 로 그 다음에 마루를 깔다 ~하지 않는 한 우리 가지고 있다 로 개방된 그 문들 여기.     LET eState == 엘레베이터스테이트[e] 인     LET 다음 층 == IF eState.방향 = "업" 그럼 eState.마루를 깔다 + 1 기타 eState.마루를 깔다 - 1 인     /\ eState.방향 /= "스테이션"     /\ ~eState.문이 열려 있다     /\ eState.마루를 깔다 \공증인 eState.단추 누름     /\ \A 부르다 \에 액티브엘레베이터콜스 : \* 캔 움직이다 단 한 가지 만일 타사의 엘리베이터를 타다 서비스하는 부르다         /\ 캔서비스콜[e, 부르다] =>             /\ \E e2 \에 엘리베이터 :                 /\ e /= e2                 /\ 캔서비스콜[e2, 부르다]     /\ 다음 층 \에 바닥     /\ 엘레베이터스테이트' = [엘레베이터스테이트 제외 ![e] = [@ 제외 !.마루를 깔다 = 다음 층]]     /\ 변경되지 않음 <<퍼스널스테이트, 액티브엘레베이터콜스>>  스톱엘레베이터(e) == \* 스톱스 그 엘리베이터를 타다 만일 너무 좋다 옮겨진 로서 먼 곳에 로서 그럭저럭 통조림 에 하나 방향     LET eState == 엘레베이터스테이트[e] 인     LET 다음 층 == IF eState.방향 = "업" 그럼 eState.마루를 깔다 + 1 기타 eState.마루를 깔다 - 1 인     /\ ~가능한 오픈엘레베이터도어(e)     /\ ~eState.문이 열려 있다     /\ 다음 층 \공증인 바닥     /\ 엘레베이터스테이트' = [엘레베이터스테이트 제외 ![e] = [@ 제외 !.방향 = "스테이션"]]     /\ 변경되지 않음 <<퍼스널스테이트, 액티브엘레베이터콜스>>  (***************************************************************************) (* 이것 액션 선택하다 a의 엘리베이터를 타다 로 서비스 그 부르다. 그 소박한         *) (* 알고리즘. 고른 것 그 가장 가까운 엘리베이터를 타다 어떤 것 이다 어느 쪽이든 고정된 또는      *) (* 이미 감동적인 향하여 그 부르다 마루를 깔다 에 그 같은 방향 로서 그 부르다. *) (* 그 계통 유지한다 아니요. 기록하다 의 할당 a의 엘리베이터를 타다 로 서비스 a 부르다.  *) (* 그것 이다 가능한 아니요. 엘리베이터를 타다 이다 수완이 로 서비스 a 부르다, 그렇지만 우리 이다        *) (* 보장된 a의 엘리베이터를 타다 할 것이다 종국에는 되다 이용할 수 있는.                *) (***************************************************************************) 디스패치엘레베이터(c) ==     LET 고정된 == {e \에 엘리베이터 : 엘레베이터스테이트[e].방향 = "스테이션"} 인     LET 다가오는 == {e \에 엘리베이터 :         /\ 엘레베이터스테이트[e].방향 = c.방향         /\  \/ 엘레베이터스테이트[e].마루를 깔다 = c.마루를 깔다             \/ GetDirection[엘레베이터스테이트[e].마루를 깔다, c.마루를 깔다] = c.방향 } 인     /\ c \에 액티브엘레베이터콜스     /\ 고정된 \컵을 다가오는 /= {}     /\ 엘레베이터스테이트' =          LET 가장 가까운 == 선택 e \에 고정된 \컵을 다가오는 :             /\ \A e2 \에 고정된 \컵을 다가오는 :                 /\ GetDistance[엘레베이터스테이트[e].마루를 깔다, c.마루를 깔다] <= GetDistance[엘레베이터스테이트[e2].마루를 깔다, c.마루를 깔다] 인         IF 가장 가까운 \에 고정된         그럼 [엘레베이터스테이트 제외 ![가장 가까운] = [@ 제외 !.마루를 깔다 = c.마루를 깔다, !.방향 = c.방향]]         기타 엘레베이터스테이트     /\ 변경되지 않음 <<퍼스널스테이트, 액티브엘레베이터콜스>>  초기화 == \* 초기화 사람 그리고 엘리베이터 로 임의의 층층     /\ 퍼스널스테이트 \에 [사람 -> [위치 : 바닥, 목적지 : 바닥, 기다림 : {거짓의}]]     /\ 액티브엘레베이터콜스 = {}     /\ 엘레베이터스테이트 \에 [엘리베이터 -> [마루를 깔다 : 바닥, 방향 : {"스테이션"}, 문이 열려 있다 : {거짓의}, 단추 누름 : {{}}]]  다음 == \* 그 다음에-주 관계     \/ \E p \에 사람 : 픽뉴데스티네이션(p)     \/ \E p \에 사람 : 콜엘레베이터(p)     \/ \E e \에 엘리베이터 : 오픈엘레베이터도어(e)     \/ \E e \에 엘리베이터 : EnterElevator(e)     \/ \E e \에 엘리베이터 : 엑시트엘레베이터(e)     \/ \E e \에 엘리베이터 : 클로즈엘레베이터도어(e)     \/ \E e \에 엘리베이터 : 무브엘레베이터(e)     \/ \E e \에 엘리베이터 : 스톱엘레베이터(e)     \/ \E c \에 엘리베이터콜 : 디스패치엘레베이터(c)  시간적 가정 ==  \* 가정 에 관하여 어떻게 엘리베이터 그리고 사람 할 것이다 얌전하게 굴다     /\ \A p \에 사람 : WF_Vars(콜엘레베이터(p))     /\ \A e \에 엘리베이터 : WF_Vars(오픈엘레베이터도어(e))     /\ \A e \에 엘리베이터 : WF_Vars(EnterElevator(e))     /\ \A e \에 엘리베이터 : WF_Vars(엑시트엘레베이터(e))     /\ \A e \에 엘리베이터 : SF_Vars(클로즈엘레베이터도어(e))     /\ \A e \에 엘리베이터 : SF_Vars(무브엘레베이터(e))     /\ \A e \에 엘리베이터 : WF_Vars(스톱엘레베이터(e))     /\ \A c \에 엘리베이터콜 : SF_Vars(디스패치엘레베이터(c))  스펙 == \* 초기화 주 와 함께 초기화 그리고 전이 와 함께 다음, 주제 로 시간적 가정     /\ 초기화     /\ [][다음]_vars     /\ 시간적 가정  정리 스펙 => [](타이프인바리안트 /\ 세이프티인바리안트 /\ 시간 인바리어트)  =============================================================================

참고 항목

참조

^ ^a ^b Lamport, Leslie (January 2000). Specifying Concurrent Systems with TLA⁺ (PDF). NATO Science Series, III: Computer and Systems Sciences. Vol. 173. IOS Press, Amsterdam. pp. 183–247. ISBN 978-90-5199-459-9. Retrieved 22 May 2015.
^ ^a ^b Lamport, Leslie (15 January 2014). "TLA⁺²: A Preliminary Guide" (PDF). Retrieved 2 May 2015.
^ "Tlaplus Tools - License". CodePlex. Microsoft, Compaq. 8 April 2013. Retrieved 10 May 2015. https://tlaplus.codeplex.com/license
^ ^a ^b Newcombe, Chris; Rath, Tim; Zhang, Fan; Munteanu, Bogdan; Brooker, Marc; Deardeuff, Michael (29 September 2014). "Use of Formal Methods at Amazon Web Services" (PDF). Amazon. Retrieved 8 May 2015.
^ Lamport, Leslie (25 January 2013). "Why We Should Build Software Like We Build Houses". Wired. Wired. Retrieved 7 May 2015.
^ Lamport, Leslie (18 June 2002). "7.1 Why Specify". Specifying Systems: The TLA⁺ Language and Tools for Hardware and Software Engineers. Addison-Wesley. p. 75. ISBN 978-0-321-14306-8. Having to describe a design precisely often reveals problems - subtle interactions and "corner cases" that are easily overlooked.
^ Lamport, Leslie (2012). "How to Write a 21st Century Proof" (PDF). Journal of Fixed Point Theory and Applications. 11: 43–63. doi:10.1007/s11784-012-0071-6. ISSN 1661-7738. Retrieved 23 May 2015.
^ Øhrstrøm, Peter; Hasle, Per (1995). "3.7 Temporal Logic and Computer Science". Temporal Logic: From Ancient Ideas to Artificial Intelligence. Studies in Linguistics and Philosophy. Vol. 57. Springer Netherlands. pp. 344–365. doi:10.1007/978-0-585-37463-5. ISBN 978-0-7923-3586-3.
^ Lamport, Leslie. "The Writings of Leslie Lamport: Proving the Correctness of Multiprocess Programs". Retrieved 22 May 2015.
^ Lamport, Leslie. "The Writings of Leslie Lamport: On-the-fly Garbage Collection: an Exercise in Cooperation". Retrieved 22 May 2015.
^ Lamport, Leslie. "The Writings of Leslie Lamport: 'Sometime' is Sometimes 'Not Never'". Retrieved 22 May 2015.
^ ^a ^b Lamport, Leslie. "The Writings of Leslie Lamport: Specifying Concurrent Programming Modules". Retrieved 22 May 2015.
^ Lamport, Leslie. "The Writings of Leslie Lamport: The Temporal Logic of Actions". Retrieved 22 May 2015.
^ ^a ^b Yu, Yuan; Manolios, Panagiotis; Lamport, Leslie (1999). Model checking TLA⁺ specifications (PDF). Correct Hardware Design and Verification Methods. Lecture Notes in Computer Science. Vol. 1703. Springer-Verlag. pp. 54–66. doi:10.1007/3-540-48153-2_6. ISBN 978-3-540-66559-5. Retrieved 14 May 2015.
^ Lamport, Leslie (18 June 2002). Specifying Systems: The TLA⁺ Language and Tools for Hardware and Software Engineers. Addison-Wesley. ISBN 978-0-321-14306-8.
^ Lamport, Leslie (2 January 2009). The PlusCal Algorithm Language (PDF). Lecture Notes in Computer Science. Vol. 5684. Springer Berlin Heidelberg. pp. 36–60. doi:10.1007/978-3-642-03466-4_2. ISBN 978-3-642-03465-7. Retrieved 10 May 2015.
^ ^a ^b ^c ^d Cousineau, Denis; Doligez, Damien; Lamport, Leslie; Merz, Stephan; Ricketts, Daniel; Vanzetto, Hernán (1 January 2012). TLA⁺ Proofs (PDF). FM 2012: Formal Methods. Lecture Notes in Computer Science. Vol. 7436. Springer Berlin Heidelberg. pp. 147–154. doi:10.1007/978-3-642-32759-9_14. ISBN 978-3-642-32758-2. Retrieved 14 May 2015.
^ Lamport, Leslie (18 June 2002). "8.9.2 Machine Closure". Specifying Systems: The TLA⁺ Language and Tools for Hardware and Software Engineers. Addison-Wesley. p. 112. ISBN 978-0-321-14306-8. We seldom want to write a specification that isn't machine closed. If we do write one, it's usually by mistake.
^ Lamport, Leslie (18 June 2002). "8.9.6 Temporal Logic Considered Confusing". Specifying Systems: The TLA⁺ Language and Tools for Hardware and Software Engineers. Addison-Wesley. p. 116. ISBN 978-0-321-14306-8. Indeed, [most engineers] can get along quite well with specifications of the form (8.38) that express only safety properties and don't hide any variables.
^ Markus A. Kuppe (3 June 2014). Distributed TLC (Recording of technical talk). TLA⁺ Community Event 2014, Toulouse, France.{{cite AV media}}: CS1 maint : 위치(링크)
^ "Unsupported TLAPS features". TLA⁺ Proof System. Microsoft Research - INRIA Joint Centre. Retrieved 14 May 2015.
^ Koutanov, Emil (12 July 2021). "Spire: A Cooperative, Phase-Symmetric Solution to Distributed Consensus". IEEE Access. IEEE. Retrieved 6 Sep 2021.
^ TLA+ 증명 시스템
^ Leslie Lamport (3 April 2014). Thinking for Programmers (at 21m46s) (Recording of technical talk). San Francisco: Microsoft. Retrieved 14 May 2015.
^ Chris, Newcombe (2014). Why Amazon Chose TLA⁺. Lecture Notes in Computer Science. Vol. 8477. Springer Berlin Heidelberg. pp. 25–39. doi:10.1007/978-3-662-43652-3_3. ISBN 978-3-662-43651-6.
^ Lardinois, Frederic (10 May 2017). "With Cosmos DB, Microsoft wants to build one database to rule them all". TechCrunch. Retrieved 10 May 2017.
^ Leslie Lamport (10 May 2017). Foundations of Azure Cosmos DB with Dr. Leslie Lamport (Recording of interview). Microsoft Azure. Retrieved 10 May 2017.

외부 링크

TLA 홈 페이지, TLA⁺ 도구 및 리소스에 연결된 레슬리 램포트의 웹 페이지
레슬리 램포트의 TLA⁺ 교과서 TLA⁺ 하이퍼북
Amazon Web Services의 공식 방법, 2015년 4월 ACM 통신의 기사
프로그래머를 위한 생각, 2014 빌드에서 레슬리 램포트의 강연
2014년 Microsoft Research 교수진 회의에서 레슬리 램포트가 한 강연
누가 청사진을 그리지 않고 초고층 건물을 짓는가? 2014년 샌프란시스코 리액션에서 레슬리 램포트의 강연이다.
프로그래밍은 코딩 그 이상이어야 한다, 레슬리 램포트의 2015년 스탠포드 강연
알고리즘을 쓴 유클리드: 동화, 맨프레드 브로이를 위한 축제에 포함된 레슬리 램포트의 TLA⁺ 소개
TLA⁺ Google 그룹

[tlaplus-original-1] Lamport, Leslie (January 2000). Specifying Concurrent Systems with TLA⁺ (PDF). NATO Science Series, III: Computer and Systems Sciences. Vol. 173. IOS Press, Amsterdam. pp. 183–247. ISBN 978-90-5199-459-9. Retrieved 22 May 2015.

[tla2guide-2] Lamport, Leslie (15 January 2014). "TLA⁺²: A Preliminary Guide" (PDF). Retrieved 2 May 2015.

[toolboxlicense-3] "Tlaplus Tools - License". CodePlex. Microsoft, Compaq. 8 April 2013. Retrieved 10 May 2015. https://tlaplus.codeplex.com/license

[awsorig-4] Newcombe, Chris; Rath, Tim; Zhang, Fan; Munteanu, Bogdan; Brooker, Marc; Deardeuff, Michael (29 September 2014). "Use of Formal Methods at Amazon Web Services" (PDF). Amazon. Retrieved 8 May 2015.

[wired-5] Lamport, Leslie (25 January 2013). "Why We Should Build Software Like We Build Houses". Wired. Wired. Retrieved 7 May 2015.

[precise-spec-6] Lamport, Leslie (18 June 2002). "7.1 Why Specify". Specifying Systems: The TLA⁺ Language and Tools for Hardware and Software Engineers. Addison-Wesley. p. 75. ISBN 978-0-321-14306-8. Having to describe a design precisely often reveals problems - subtle interactions and "corner cases" that are easily overlooked.

[lamport-proofs-7] Lamport, Leslie (2012). "How to Write a 21st Century Proof" (PDF). Journal of Fixed Point Theory and Applications. 11: 43–63. doi:10.1007/s11784-012-0071-6. ISSN 1661-7738. Retrieved 23 May 2015.

[temporal-logic-history-8] Øhrstrøm, Peter; Hasle, Per (1995). "3.7 Temporal Logic and Computer Science". Temporal Logic: From Ancient Ideas to Artificial Intelligence. Studies in Linguistics and Philosophy. Vol. 57. Springer Netherlands. pp. 344–365. doi:10.1007/978-0-585-37463-5. ISBN 978-0-7923-3586-3.

[lamport-proving-9] Lamport, Leslie. "The Writings of Leslie Lamport: Proving the Correctness of Multiprocess Programs". Retrieved 22 May 2015.

[lamport-garbage-10] Lamport, Leslie. "The Writings of Leslie Lamport: On-the-fly Garbage Collection: an Exercise in Cooperation". Retrieved 22 May 2015.

[lamport-sometime-11] Lamport, Leslie. "The Writings of Leslie Lamport: 'Sometime' is Sometimes 'Not Never'". Retrieved 22 May 2015.

[lamport-spec-12] Lamport, Leslie. "The Writings of Leslie Lamport: Specifying Concurrent Programming Modules". Retrieved 22 May 2015.

[lamport-actions-13] Lamport, Leslie. "The Writings of Leslie Lamport: The Temporal Logic of Actions". Retrieved 22 May 2015.

[tlcoriginal-14] Yu, Yuan; Manolios, Panagiotis; Lamport, Leslie (1999). Model checking TLA⁺ specifications (PDF). Correct Hardware Design and Verification Methods. Lecture Notes in Computer Science. Vol. 1703. Springer-Verlag. pp. 54–66. doi:10.1007/3-540-48153-2_6. ISBN 978-3-540-66559-5. Retrieved 14 May 2015.

[specsystems-15] Lamport, Leslie (18 June 2002). Specifying Systems: The TLA⁺ Language and Tools for Hardware and Software Engineers. Addison-Wesley. ISBN 978-0-321-14306-8.

[pluscal-original-16] Lamport, Leslie (2 January 2009). The PlusCal Algorithm Language (PDF). Lecture Notes in Computer Science. Vol. 5684. Springer Berlin Heidelberg. pp. 36–60. doi:10.1007/978-3-642-03466-4_2. ISBN 978-3-642-03465-7. Retrieved 10 May 2015.

[tlaps-survey-17] Cousineau, Denis; Doligez, Damien; Lamport, Leslie; Merz, Stephan; Ricketts, Daniel; Vanzetto, Hernán (1 January 2012). TLA⁺ Proofs (PDF). FM 2012: Formal Methods. Lecture Notes in Computer Science. Vol. 7436. Springer Berlin Heidelberg. pp. 147–154. doi:10.1007/978-3-642-32759-9_14. ISBN 978-3-642-32758-2. Retrieved 14 May 2015.

[machine-closure-18] Lamport, Leslie (18 June 2002). "8.9.2 Machine Closure". Specifying Systems: The TLA⁺ Language and Tools for Hardware and Software Engineers. Addison-Wesley. p. 112. ISBN 978-0-321-14306-8. We seldom want to write a specification that isn't machine closed. If we do write one, it's usually by mistake.

[temporal-logic-confusing-19] Lamport, Leslie (18 June 2002). "8.9.6 Temporal Logic Considered Confusing". Specifying Systems: The TLA⁺ Language and Tools for Hardware and Software Engineers. Addison-Wesley. p. 116. ISBN 978-0-321-14306-8. Indeed, [most engineers] can get along quite well with specifications of the form (8.38) that express only safety properties and don't hide any variables.

[tlcdistributed-20] Markus A. Kuppe (3 June 2014). Distributed TLC (Recording of technical talk). TLA⁺ Community Event 2014, Toulouse, France.{{cite AV media}}: CS1 maint : 위치(링크)

[tlaps-unsupported-21] "Unsupported TLAPS features". TLA⁺ Proof System. Microsoft Research - INRIA Joint Centre. Retrieved 14 May 2015.

[spire-22] Koutanov, Emil (12 July 2021). "Spire: A Cooperative, Phase-Symmetric Solution to Distributed Consensus". IEEE Access. IEEE. Retrieved 6 Sep 2021.

[23] TLA+ 증명 시스템

[lamportbuild-24] Leslie Lamport (3 April 2014). Thinking for Programmers (at 21m46s) (Recording of technical talk). San Francisco: Microsoft. Retrieved 14 May 2015.

[awschose-25] Chris, Newcombe (2014). Why Amazon Chose TLA⁺. Lecture Notes in Computer Science. Vol. 8477. Springer Berlin Heidelberg. pp. 25–39. doi:10.1007/978-3-662-43652-3_3. ISBN 978-3-662-43651-6.

[cosmos-26] Lardinois, Frederic (10 May 2017). "With Cosmos DB, Microsoft wants to build one database to rule them all". TechCrunch. Retrieved 10 May 2017.

[lamportcosmos-27] Leslie Lamport (10 May 2017). Foundations of Azure Cosmos DB with Dr. Leslie Lamport (Recording of interview). Microsoft Azure. Retrieved 10 May 2017.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

Search