비선형 차원성 감소

2, 3차원이 넘는 데이터를 의미하는 고차원 데이터는 해석이 어려울 수 있다.단순화에 대한 한 가지 접근방식은 관심 데이터가 저차원 공간 내에 있다고 가정하는 것이다.관심 있는 데이터가 충분히 낮은 차원이라면 저차원 공간에서 데이터를 시각화할 수 있다.

아래는 비선형 치수 감소를 위한 몇 가지 주목할 만한 방법을 요약한 것이다.^[1][2]이러한 비선형 차원성 감소 방법 중 다수는 아래에 열거된 선형 방법과 관련이 있다.비선형 방법은 크게 두 가지 그룹으로 분류할 수 있다: 매핑을 제공하는 그룹(고차원 공간에서 저차원 임베딩으로 또는 그 반대로)과 시각화만 제공하는 그룹이다.

관련 선형 분해 방법

• 독립 성분 분석(ICA)
• 주성분 분석(PCA) - Karhunen-Loeve 정리라고도 함 - KLT
• 단수 값 분해(SVD)
• 인자분석

NLDR의 적용

매트릭스(또는 데이터베이스 테이블)로 표시된 데이터 집합을 고려하십시오. 예를 들어 각 행은 특정 사물의 인스턴스를 설명하는 속성(또는 형상 또는 치수) 집합을 나타낸다.속성 수가 크면 가능한 고유 행의 공간이 기하급수적으로 커진다.따라서 차원성이 클수록 공간 표본 추출이 어려워진다.이것은 많은 문제를 일으킨다.고차원 데이터에서 작동하는 알고리즘은 시간 복잡성이 매우 높은 경향이 있다.예를 들어 많은 머신러닝 알고리즘이 고차원 데이터로 인해 어려움을 겪고 있다.데이터를 더 적은 차원으로 줄이는 것은 종종 분석 알고리즘을 더 효율적으로 만들고, 기계 학습 알고리즘이 더 정확한 예측을 하는데 도움을 줄 수 있다.

인간은 종종 높은 차원의 데이터를 이해하는 데 어려움을 겪는다.따라서 데이터를 소수의 차원으로 줄이는 것이 시각화 목적에 유용하다.

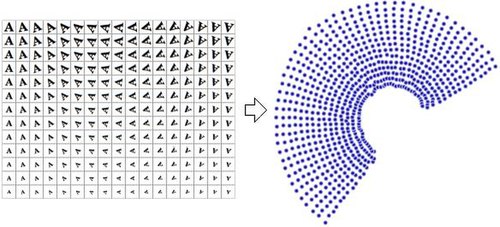
데이터의 축소된 표현은 흔히 "내적 변수"라고 불린다.이 설명은 데이터가 생성되는 값이라는 것을 의미한다.예를 들어, 다양한 양으로 확장 및 회전된 문자 'A'의 이미지가 포함된 데이터 집합을 고려해 보십시오.각 이미지는 32x32 픽셀이다.각각의 이미지는 1024 픽셀 값의 벡터로 표현될 수 있다.각 행은 1024차원 공간(해밍 공간)에 있는 2차원 다지관의 표본이다.데이터를 생성하기 위해 두 변수(회전 및 척도)가 달라졌기 때문에 내적 차원성은 두 가지다.문자 'A'의 모양이나 모양에 대한 정보는 모든 경우에 동일하기 때문에 내재 변수의 일부가 아니다.비선형 치수 감소는 상관된 정보(문자 'A')를 버리고 다양한 정보(회전 및 척도)만 복구한다.오른쪽의 이미지는 이 데이터 집합의 샘플 영상(모든 입력 영상이 표시되는 것은 아니고 공간을 절약하기 위해)과 데이터를 단 2차원으로 줄이기 위해 NLDR 알고리즘(이 경우 다지관 조각이 사용됨)을 사용한 2차원 점의 플롯을 보여준다.

그에 비해, 선형 차원성 감소 알고리즘인 주성분 분석을 사용하여 동일한 데이터 집합을 2차원으로 줄인다면, 결과 값은 그리 잘 정리되지 않는다.이는 이 다지관을 표본으로 추출하는 고차원 벡터(각각 문자 'A'를 나타냄)가 비선형 방식으로 변화한다는 것을 보여준다.

따라서 NLDR은 컴퓨터 비전 분야에서 여러 가지 응용 프로그램을 가지고 있다는 것이 명백해야 한다.예를 들어, 카메라를 사용하여 닫힌 정적 환경에서 탐색하는 로봇을 생각해 보십시오.해당 카메라가 획득한 영상은 고차원 공간의 다지관에 있는 샘플로 간주할 수 있으며, 다지관의 내재가변수는 로봇의 위치와 방향을 나타낸다.

불변 다지관은 동적 시스템의 모델 순서 감소에 일반적으로 관심이 있다.특히 위상공간에 매력적인 불변 다지관이 있을 경우 인근 궤도가 그 위로 모여 무한정 유지돼 동적계통의 입체감소 후보지가 된다.그러한 다지관은 일반적으로 존재한다고 보장되지 않지만, 스펙트럼 하위매니폴즈(SSM) 이론은 광범위한 종류의 동적 시스템에서 고유한 유인 불변 물체의 존재에 대한 조건을 제시한다.^[3]NLDR의 적극적인 연구는 동적 시스템과 관련된 관측 다지관을 펼쳐 모델링 기법을 개발하고자 한다.^[4]

보다 두드러진 비선형 차원성 감소 기법 중 일부는 아래에 열거되어 있다.

중요 개념

삼몬의 지도

Sammon의 매핑은 가장 처음이자 가장 인기 있는 NLDR 기술 중 하나이다.

자기조직지도

자기조직지도(SOM, Kohonen map이라고도 한다)와 그 확률론적 변종생성 지형지도(GTM)는 내장공간에서 점표현상을 사용하여 내장공간에서 고차원 공간에 이르는 비선형 매핑을 기반으로 잠재 변수 모델을 형성한다.^[6]이러한 기법들은 밀도 네트워크에서의 작업과 관련이 있으며, 또한 동일한 확률론적 모델을 기반으로 한다.

커널 주성분 분석

아마도 치수 축소를 위해 가장 널리 사용되는 알고리즘은 커널 PCA일 것이다.^[7]PCA는 $m{\displaystyle }$ ${\displaystyle \times }$ ${\displaystyle n}$ ${\displaystyle m\times n}$ 행렬$$ $X{\displaystyle \mathbf{}}$ ${\$의 공분산 행렬을 계산하는 것으로 시작한다$.$

${\displaystyle C={\frac {1}{m}\sum _{i=1}^{m}{m}{\mathbf {x} _{i}^{\mathsf {T}}}.}$

그런 다음 데이터를 이 행렬의 첫 번째 고유 벡터에 투영한다.이에 비해 KPCA는 고차원 공간으로 변환된 후 데이터의 공분산 행렬을 계산하는 것으로 시작한다.

${\displaystyle C={\frac {1}{m}\sum _{i=1}^{m}{\Phi(\mathbf {x} _{i})\Phi(\mathbf {x} _{i}^{\mathsf {T}}).}$

그런 다음 변환된 데이터를 PCA와 마찬가지로 매트릭스의 첫 번째 고유 벡터에 투영한다.실제 $\phi {\displaystyle \mathrm{}}$($){\displaystyle \Phi (\mathbf {x}}}}$을(를) 계산하지 않고 전체 프로세스를 수행할 수 있도록 커널 트릭을 많이 사용하여 계산한다$.$ 물론 $\phi {\displaystyle \mathrm{}}$ ${\displaystyle \Phi }$은(으)로 알려진 커널을 가질 수 있도록 선택해야 한다$$.불행히도 주어진 문제에 대해 좋은 커널을 찾는 것은 사소한 일이 아니기 때문에, KPCA는 표준 커널을 사용할 때 몇 가지 문제로 좋은 결과를 내지 못한다.예를 들어, 스위스 롤 다지관에서 이러한 커널로 성능이 떨어지는 것으로 알려져 있다.단, 데이터에 의존하는 커널 매트릭스를 구성함으로써, 그러한 설정(예: Laplacian Eigenmaps, LLE)에서 잘 수행되는 특정 다른 방법들을 커널 PCA의 특별한 사례로 볼 수 있다.^[8]

KPCA는 내부 모델을 갖고 있어 교육 당시에는 이용할 수 없었던 임베딩에 포인트를 매핑하는 데 활용할 수 있다.

주 곡선 및 다지관

주곡선과 다지관은 비선형 치수 감소를 위한 자연적인 기하학적 프레임워크를 제공하며, 내장 다지관을 명시적으로 구성하고 다지관에 표준 기하학적 투영을 사용하여 인코딩함으로써 PCA의 기하학적 해석을 확장한다.이 접근법은 원래 트레버 헤스티가 1989년에 정식으로 소개한 1984년 논문에서 제안한 것이다.^[12][13]이 생각은 많은 작가들에 의해 더욱 탐구되었다.^[14]다지관의 "단순성"을 정의하는 방법은 문제에 따라 다르지만, 일반적으로 다지관의 내적인 차원성 및/또는 부드러움에 의해 측정된다.일반적으로 주 매니폴드는 최적화 문제에 대한 해결책으로 정의된다.목표 함수는 데이터 근사치의 품질과 다지관 벤딩에 대한 일부 벌칙 항을 포함한다.일반적인 초기 근사치는 선형 PCA와 코호넨의 SOM에 의해 생성된다.

라플라시안 아이겐맵스

라플라시안 고유맵은 스펙트럼 기법을 사용하여 치수 감소를 수행한다.^[15]이 기법은 데이터가 고차원 공간의 저차원 다지관에 있다는 기본적인 가정에 의존한다.^[16]이 알고리즘은 샘플 외 포인트를 내장할 수 없지만, Replicating 커널 Hilbert 공간 정규화에 기반한 기술은 이 기능을 추가하기 위해 존재한다.^[17]이러한 기법은 다른 비선형 차원성 감소 알고리즘에도 적용할 수 있다.

주성분 분석과 같은 기존 기법에서는 데이터의 고유 지오메트리를 고려하지 않는다.라플라시안 고유맵은 데이터 세트의 인접 정보로부터 그래프를 만든다.각 데이터 포인트는 그래프의 노드 역할을 하며 노드 간의 연결은 인접 포인트의 근접성에 의해 제어된다(예: k-가장 가까운 이웃 알고리즘 사용).따라서 생성된 그래프는 고차원 공간에서 저차원 다지관의 이산적 근사치로 간주할 수 있다.그래프를 기반으로 비용 함수를 최소화하면 다지관의 서로 가까운 지점이 저차원 공간에서 서로 가까이 매핑되어 국지적 거리를 보존할 수 있다.온화한 조건에서 이 운영자는 다지관의 정사각형 통합 기능을 위한 기초가 되는 계수 가능한 스펙트럼을 갖기 때문에(단위 원 다지관의 푸리에 시리즈와 비교) 다지관의 라플라스-벨트라미 운영자의 고유 기능은 내장 치수로 사용된다.라플라시안 고유맵을 견고한 이론적 토대 위에 배치하려는 시도는 어느 정도 성공을 거두었는데, 특정한 비제한적 가정 하에서 그래프의 라플라스-벨트라미 연산자(Laplacian matrix)는 점의 수가 무한대로 가면서 라플라스-벨트라미 연산자로 수렴되는 것으로 나타났다.^[16]

이소맵

이소맵은^[18] 플로이드-워셜 알고리즘과 고전적인 다차원 스케일링을 조합한 것이다.고전적 다차원 스케일링(MDS)은 모든 점 사이의 쌍방향 거리 행렬을 취하여 각 점의 위치를 계산한다.이소맵은 쌍방향 거리는 인접한 지점들 사이에만 알려져 있다고 가정하고 플로이드-워셜 알고리즘을 사용하여 다른 모든 지점들 간의 쌍방향 거리를 계산한다.이것은 모든 점 사이의 쌍방향 지오데틱 거리의 전체 행렬을 효과적으로 추정한다.이후 Isomap은 고전적인 MDS를 사용하여 모든 점의 축소된 차원 위치를 계산한다.랜드마크-이소맵은 어느 정도 정확성을 희생시키면서 속도를 높이기 위해 랜드마크를 사용하는 이 알고리즘의 변형이다.

다지관 학습에서 입력 데이터는 고차원 벡터 공간 내부에 내장된 저차원 다지관으로부터 샘플링되는 것으로 가정한다.MVU 뒤에 있는 주요 직관은 다지관의 국부적 선형성을 이용하고 기초 다지관의 모든 지점에서 국부적 인접성을 보존하는 지도를 만드는 것이다.

로컬 선형 임베딩

LLE(^[19]Local-Linear Embedding)는 Isomap과 거의 동시에 제시되었다.스파스 매트릭스 알고리즘을 활용하기 위해 구현했을 때 더 빠른 최적화와 많은 문제를 안고 더 나은 결과를 얻는 등 이소맵에 비해 몇 가지 장점이 있다.LLE는 또한 각 점의 가장 가까운 이웃들의 집합을 찾는 것으로 시작한다.그런 다음, 점을 가장 잘 설명하는 각 점의 가중치 집합을 이웃의 선형 조합으로 계산한다.마지막으로, 그것은 고유 벡터 기반의 최적화 기법을 사용하여 포인트의 저차원 내장 방법을 찾아내어, 각각의 포인트가 여전히 이웃의 동일한 선형 결합으로 설명되도록 한다.LLE는 다양한 지역의 표본 밀도가 다르기 때문에 가중치가 표류하지 않도록 고정된 단위가 없기 때문에 균일하지 않은 표본 밀도를 잘 처리하는 경향이 있다.LLE는 내부 모델이 없다.

LLE는 주변 X에_j 근거하여 점 X의_i 편심 좌표를 계산한다.원래 점은 인접한 무게 행렬 W에_ij 의해 주어진 선형 조합에 의해 재구성된다.재구성 오류는 비용 함수 E(W)에 의해 주어진다.

${\displaystyle E(W)=\sum _{i} {i}-\sum _{j}{{j}{\mathbf {W} _{ij}\mathbf {X} _{j}}}^{}}}}{\mathsf {2}}}$

W_ij 가중치는 X점이_j X점을_i 재구성할 때 갖는 기여도를 가리킨다.비용 함수는 다음과 같은 두 가지 제약조건으로 최소화된다. (a) 각 데이터 지점 X는_i 인접 지점에서만 재구성된다. 따라서 지점_ji X와 (b) 지점 X의 인접 지점이 아닌 경우 W를_ij 0으로 강제 W는 0이다.

${\displaystyle \sum _{j}{\mathbf {W} _{ij}=1}$

원래의 데이터 포인트는 D 치수 공간에서 수집되며 알고리즘의 목표는 치수성을 D >> d와 같은 d로 줄이는 것이다.D 치수 공간에서 ih 데이터 점을 재구성하는 동일한 가중치 W를_ij 사용하여 더 낮은 d 치수 공간에서 동일한 점을 재구성한다.이런 생각을 바탕으로 동네 보존 지도가 만들어진다.D 차원 공간의 각 X_i 점을 비용 함수를 최소화하여 D 차원 공간의 Y 지점에_i 매핑

${\displaystyle C(Y)=\sum _{i}{i}-\sum _{j}{{j}{\mathbf {W} _{ij}\mathbf {J}}}^{}}{j}}}}}{\mathsf {2}}}$

이 비용함수에서는 이전과 달리 W 가중치를_ij 고정하고 Y_i 지점에서 최소화를 수행하여 좌표를 최적화한다.이러한 최소화 문제는 희박한 N X N 고유값 문제(N은 데이터 포인트의 수임)를 해결하여 해결할 수 있으며, 이 문제의 하단 d 논제로 고유 벡터는 직교 좌표 세트를 제공한다.일반적으로 데이터 점은 유클리드 거리로 측정한 K 가장 가까운 이웃으로부터 재구성된다.그러한 구현을 위해 알고리즘에는 교차 검증으로 선택할 수 있는 자유 매개변수 K가 하나만 있다.

헤시안 로컬-선형 임베딩(헤시안 LLE)

Hesian LLE도 LLE와 마찬가지로 희박한 행렬 기법에 기초하고 있다.^[20]그것은 LLE보다 훨씬 높은 품질의 결과를 산출하는 경향이 있다.불행하게도, 그것은 매우 비싼 계산 복잡성을 가지고 있어서, 심하게 샘플링된 다지관에는 적합하지 않다.그것은 내부 모델이 없다.

수정된 로컬-선형 임베딩(MLLE)

MLLE(Modified LLE)^[21]는 LLE 맵의 왜곡을 초래하는 국소 중량 매트릭스 조절 문제를 해결하기 위해 각 동네에서 복수의 가중치를 사용하는 또 다른 LLE 변종이다.느슨하게 말하면 다중 가중치는 LLE에 의해 생성된 원래 가중치의 국소 직교 투영이다.이 정규화된 변종의 작성자는 또한 LTSA(Local Tangent Space Alignment)의 저자로, 각 중량 벡터의 직교 투영의 전역 최적화가 모든 데이터 포인트의 국부 접선 공간을 정렬한다는 것을 실현할 때 MLLE 공식에 내포되어 있다.이 알고리즘의 정확한 적용에 의한 이론적, 경험적 함의는 광범위하다.^[22]

로컬 접선 공간 정렬

LTSA는^[23] 다지관을 올바르게 펼치면 다지관에 연결된 모든 접선 하이퍼플레인이 정렬된다는 직관에 기초한다.그것은 모든 점에서 가장 가까운 이웃들을 계산하는 것으로 시작된다.그것은 각 지역 동네의 d-first 주요 요소들을 계산하여 모든 지점의 접선 공간을 계산한다.그런 다음 접선 공간을 정렬하는 내장을 찾도록 최적화한다.

최대 분산 전개

최대 분산 전개, 이소맵 및 로컬 선형 임베딩은 다지관이 적절히 펼쳐지면 점들에 대한 분산이 극대화된다는 개념에 의존하는 공통의 직관을 공유한다.Isomap과 Local Linear Embedding과 같은 그것의 초기 단계는 모든 점에서 가장 가까운 이웃을 찾는 것이다.그런 다음 인접 지점 사이의 거리가 보존되도록 제약된 모든 인접 지점 사이의 거리를 최대화하는 문제를 해결하려고 한다.이 알고리즘의 일차적 기여는 이 문제를 세미더파인 프로그래밍 문제로 캐스팅하는 기법이다.불행히도, 세미데파인 프로그래밍 해결사는 높은 계산 비용을 가지고 있다.Local Linear Embedding과 마찬가지로 내부 모델이 없다.

오토엔코더

자동 인코더는 신원 기능에 근사하게 훈련된 피드-포워드 신경 네트워크다.즉, 가치의 벡터에서 같은 벡터로 지도화하는 훈련을 받는다.차원성 감소 목적으로 사용할 경우, 네트워크의 숨겨진 계층 중 하나는 소수의 네트워크 단위만 포함하도록 제한된다.그러므로 네트워크는 벡터를 소수의 차원으로 인코딩한 다음 다시 원래의 공간으로 디코딩하는 방법을 배워야 한다.따라서 네트워크의 전반부는 고차원 공간에서 저차원 공간으로, 후반부는 저차원 공간에서 고차원 공간으로 지도화하는 모델이다.오토엔코더라는 개념은 꽤 오래되었지만, 딥오토엔코더의 훈련은 제한된 볼츠만 기계와 쌓인 디노이즈 오토엔코더의 사용을 통해 최근에야 가능해졌다.오토엔코더와 관련된 것은 NeuroScale 알고리즘으로, 다차원 스케일링과 삼몬 매핑(위 참조)에서 영감을 받은 스트레스 기능을 사용하여 고차원적 공간으로부터 임베디드 공간에 이르는 비선형 매핑을 학습한다.NeuroScale의 매핑은 방사상 기반 함수 네트워크를 기반으로 한다.차원성 저감을 위한 신경망의 또 다른 용도는 데이터의 접선면을 학습하게 하는 것이다.^[24]

가우스 공정 잠재 변수 모델

가우스 프로세스 잠재 변수 모델(GPLVM)^[25]은 가우스 프로세스(GP)를 사용하여 고차원 데이터의 저차원 비선형 임베딩을 찾는 확률론적 차원성 감소 방법이다.그것들은 PCA의 확률론적 공식화의 연장선이다.모형은 확률적으로 정의되며 잠재 변수는 주변화되고 모수는 우도를 최대화하여 얻는다.커널 PCA와 마찬가지로 그들은 커널 함수를 사용하여 (가우스 프로세스의 형태로) 비 선형 매핑을 형성한다.그러나, GPLVM에서 매핑은 내장형(대기형) 공간에서 데이터 공간(밀도 네트워크, GTM 등)으로 이루어지는 반면, 커널 PCA에서는 반대 방향에 있다.이것은 원래 고차원 데이터의 시각화를 위해 제안되었지만 두 관측 공간 사이에 공유 다지관 모델을 구축하기 위해 확장되었다.GPLVM과 그 많은 변형들은 특히 인간 움직임 모델링(예: 역률 제한 GPLVM, GP Dynamic Model(GPDM), 균형 잡힌 GPDM(B-GPDM) 및 위상적으로 제한된 GPDM을 위해 제안되었다.걸음걸이 분석에서 자세와 걸음걸이 다지관의 결합 효과를 포착하기 위해 다층 관절 보행 노출 다지관이 제안되었다.^[26]

T자 확률적 이웃 임베딩

t-분산 확률 이웃 임베딩(t-SNE)^[27]이 널리 사용된다.그것은 확률적인 이웃 임베딩 방법 중 하나이다.알고리즘은 고차원 공간의 데이터 점 쌍이 연관되어 있을 확률을 계산한 다음 유사한 분포를 생성하는 저차원 임베딩(datapoint)을 선택한다.

기타 알고리즘

관계투시도

관계형 투시 맵은 다차원 스케일링 알고리즘이다.알고리즘은 닫힌 다지관의 다중 입자 동적 시스템을 시뮬레이션하여 다지관의 데이터 지점의 구성을 찾는데, 여기서 데이터 지점이 입자에 매핑되고 데이터 지점 사이의 거리(또는 유사성)가 반발력을 나타낸다.다지관의 크기가 점차 커짐에 따라 다중 입자 시스템은 점차 냉각되어 데이터 포인트의 거리 정보를 반영하는 구성으로 수렴된다.

관계형 투시 지도는 양전하 입자가 공의 표면에서 자유롭게 움직이는 물리적 모델에 의해 영감을 받았다.입자 사이의 쿨롱 힘에 의해 유도된, 입자의 최소 에너지 구성은 입자 사이의 반발력의 강도를 반영할 것이다.

Relational perspective map이 소개되었다.^[28]알고리즘은 먼저 평면 토러스(flat torus)를 이미지 매니폴드로 사용한 다음 확장되었다(구, 투사 공간, 클라인 병과 같은 다른 유형의 폐쇄 매니폴드를 이미지 매니폴드로 사용하기 위해 소프트웨어 VisuMap에서).

전염 지도

전염 지도는 네트워크에서 여러 개의 전염을 사용하여 노드를 점 구름으로 매핑한다.^[29]Global cascades 모델의 경우 확산 속도는 임계값 매개 변수 $t{\displaystyle }$ ${\displaystyle \in }$[ 0${\displaystyle ,}$ ${\displaystyle 1}$] ${\displaystyle t\in [0,1]$로 조절할 수 있다$.$${\displaystyle }t{\displaystyle }$ = 0$${\$displaystyt t=0}$의 경우 전염$$ 지도는 Isomap 알고리즘과 동일하다.

곡선성분 분석

곡선 성분 분석(CCA)은 출력 공간의 작은 거리(원래 공간의 작은 거리에 초점을 맞추는 샘몬의 매핑과 반대로)에 초점을 맞추면서 최대한 원래의 거리를 보존하는 출력 공간의 포인트 구성을 찾는다.^[30]

CCA는 반복학습 알고리즘으로서 실제로 장거리(샘몬 알고리즘처럼)에 초점을 맞춘 후 점차적으로 작은 거리로 초점을 바꾼다는 점에 유의해야 한다.만약 둘 사이에 타협이 이루어져야 한다면, 작은 거리 정보는 큰 거리 정보를 덮어쓸 것이다.

CCA의 스트레스 기능은 오른쪽 Bregman 다이버전의 합계와 관련이 있다.^[31]

곡선 거리 분석

CDA는^[30] 다지관에 맞도록 자가조직 신경망을 훈련시키고 그 내장 속에 지오데틱 거리를 보존하려고 한다.곡선성분 분석(Sammon의 매핑을 확장한)을 기반으로 하지만 대신 지오데틱 거리를 사용한다.

차이점형 차원성 감소

차이점형 차원성 감소 또는 차이점맵은^[32] 데이터를 저차원 선형 하위 공간으로 전송하는 매끄러운 차이점형 매핑을 학습한다.이 방법은 데이터 지점에서 시작하는 필드를 따라 흐르는 부드러운 시간 인덱싱 벡터 필드를 위해 해결하며, 이는 저차원 선형 하위 공간에서 끝나며, 따라서 전방 및 역방향 매핑 모두에서 쌍방향 차이를 보존하려고 시도한다.

다지관 정렬

다지관 정렬은 유사한 생성 프로세스에 의해 생성된 상이한 데이터 집합이 유사한 기초 다지관 표현을 공유할 것이라는 가정을 활용한다.각각의 원래의 공간에서 공유된 다지관으로의 투영을 학습함으로써, 서신은 복구되고 한 영역의 지식은 다른 영역으로 전달될 수 있다.대부분의 다지관 정렬 기법은 두 개의 데이터 집합만 고려하지만, 그 개념은 임의로 많은 초기 데이터 집합까지 확장된다.^[33]

확산지도

확산 맵은 열 확산과 무작위 보행(Markov Chain) 사이의 관계를 활용한다. 다지관의 확산 연산자와 다지관에서 샘플링된 노드를 그래프에 정의한 함수에서 작동하는 마르코프 전환 매트릭스 사이에 유추된다.^[34]In particular, let a data set be represented by ${\displaystyle \mathbf {X} =[x_{1},x_{2},\ldots ,x_{n}]\in \Omega \subset \mathbf {R^{D}} }$. The underlying assumption of diffusion map is that the high-dimensional data lies on a low-dimensional manifold of dimension ${\displ$$aystyle \mathbf {d}$ $\}.$ X는 데이터 세트를 나타내고 $\mu {\displaystyle }$ ${\displaystyle \mu$}은$($는) X의 데이터 포인트 분포를 나타낸다.또한 X에서 점의 유사성 개념을 나타내는 커널을 정의하십시오.커널 $k{\displaystyle \mathit{}}$ ${\$에 다음 속성이^[35] 있음$$

${\displaystyle k(x,y)=k(y,x),\,}$

k는 대칭이다.

$\displaystyle k(x,y)\geq 0\qquad \forall x,y,k}$

k는 긍정을 보존하는 것이다.

따라서 개별 데이터 점을 그래프의 노드로 생각할 수 있고 커널 k는 그래프에 어떤 종류의 친화력을 정의하는 것으로 생각할 수 있다.그 그래프는 커널이 대칭이기 때문에 구성에 의해 대칭이다.여기서 튜플(X,k)에서 가역 마코프 체인을 만들 수 있다는 것을 쉽게 알 수 있다.이 기법은 다양한 분야에서 흔히 볼 수 있으며 그래프 라플라시안으로 알려져 있다.

예를 들어 그래프 K = (X,E)는 가우스 커널을 사용하여 구성할 수 있다.

${\displaystyle K_{ij}={\begin{case}e^{-\x_x_{j}\_{2}^{2}/\sigma ^{2}}&}{\cext{x_{{i}\sim x}\0&{\text}}}}}}}}}:{case}}}}}}}}}}$

위의 방정식에서 $x{\displaystyle {}_{}}$ ${\displaystyle i_{}}$~ ${\displaystyle {}_{}}$ ${\displaystyle j_{}}$ ${\$는 x ${\displaystyle i_{}}$ ${\$이(가) $x{\displaystyle {}_{}}$ ${\displaystyle j_{}}$ ${\$의 가장 가까운 이웃임을$$ 의미하므로$,$ 지오데믹 거리를 사용하여 다지관의 거리를 실제로 측정해야 한다.다지관의 정확한 구조는 구할 수 없기 때문에 가장 가까운 이웃의 경우 지질학적 거리는 유클리드 거리에 의해 근사치된다.The choice ${\displaystyle \sigma }$ modulates our notion of proximity in the sense that if ${\displaystyle \ x_{i}-x_{j}\ _{2}\gg \sigma }$ then ${\displaystyle K_{ij}=0}$ and if ${\displaystyle \ x_{i}-x_{j}\ _{2}\ll \sigma }$ then ${\displaystyle K_{ij}}$${\displaystyle {}_{}=}$ 1 ${\displaystyle K_{ij}=1$전자는 매우 적은 확산이 일어난 반면 후자는 확산 과정이 거의 완벽하다는 것을 의미한다.$\sigma {\displaystyle }$ ${\displaystyle \sigma }$을(를) 선택하기 위한 다양한 전략을 에서 확인할 수 있다$$.^[36]

$마르코프{\displaystyle }$ 행렬을 충실히 표현하려면 K ${\displaystyle$ K$}$을(를) 해당도 행렬 $D{\displaystyle }$ ${\displaystyle$ D$}$에 의해 정규화해야 한다$$$.$

${\displaystyle P=D^{-1}K.\,}$

${\displaystyle P}$ ${\displaystyle P}$은(는) 이제 마르코프 체인을 나타낸다.${\displaystyle P(}$ ${\displaystyle {}_{}}$ ${\displaystyle i_{}}$, ${\displaystyle {}_{}}$ ${\displaystyle j_{}}$) ${\displaystyle P(x_{i},x_{j}}})$는 $x{\displaystyle {}_{}}$ ${\displaystyle i_{}}$ ${\$에서 ${\displaystyle x_{}}$ j ${\$ x_${j}}}$로 한 번에 전환할$$ 확률이다$$.Similarly the probability of transitioning from ${\displaystyle x_{i}}$ to ${\displaystyle x_{j}}$ in t time steps is given by ${\displaystyle P^{t}(x_{i},x_{j})}$. Here ${\displaystyle P^{t}}$ is the matrix ${\displaystyle P}$ multiplied by itself t times.

마르코프 행렬 $P{\displaystyle }$ ${\displaystyle P}$은 데이터 집합 X의 로컬 기하학의 개념을 구성한다$$.확산 지도와 주성분 분석의 주요 차이점은 전체 데이터 세트의 상관관계를 취하는 것과 반대로 확산 지도에서 데이터의 국소적 특징만 고려한다는 것이다.

${\displaystyle K}$ ${\displaystyle K}$은 커널이 데이터 세트의 로컬 형상을 캡처한다는 의미인 데이터 세트에 대한 임의의 워크를 정의한다$$.마르코프 체인은 커널 값을 통해 빠르고 느린 전파 방향을 정의한다.걷기가 시간 내에 앞으로 전파될 때, 국소 기하학적 정보는 동적 시스템의 국소적 전환(미분방정식으로 정의)과 같은 방식으로 집계된다.^[35]확산의 은유는 가족 확산 거리 {${\displaystyle D_{}}$ t ${\$ ${\displaystyle {}_{}}$ ${\displaystyle {\in }_{}}$ ${\displaystyle N_{}}$ ${\$ N$}}$의 정의에서 비롯된다.

${\displaystyle D_{t}^{2}(x,y)=p_{t}(x,\cdot )-p_{t}(y,\cdot ) ^{2}}$

고정 t의 경우, $D{\displaystyle {}_{}}$ ${\displaystyle t_{}}$ ${\$는 경로 연결을 기반으로 데이터 집합의 두 지점 사이의 거리를 정의한다$$: D $t{\displaystyle {}_{}}$( ${\displaystyle x}$, ${\displaystyle y}$) ${\displaystyle D_{t}(x,y)}$는 x를 y에 연결하는 경로가 많을수록 더 작아지고$$ 그 반대도 된다.수량 $D{\displaystyle {}_{}}$ ${\displaystyle t_{}}$( ${\displaystyle x}$, y${\displaystyle }$) ${\displaystyle D_{t}(x,y)}$은 길이 t의 모든 경로에 대한 합을 포함하므로$$, ${\displaystyle D_{}}$ $t{\displaystyle {}_{}}$ ${\$는 측지 거리보다 데이터 노이즈에 훨씬 강하다$$.${\displaystyle D_{}}$ ${\displaystyle t_{}}$ ${\$는 거리를 계산하면서 x와 y 지점 사이의 모든 관계를 고려하며$$, 유클리드 거리나 심지어 지질학적 거리보다 근접성에 대한 더 나은 개념으로 작용한다.

로컬 다차원 스케일링

로컬 다차원 스케일링은 로컬 지역에서 다차원 스케일링을 수행한 다음 볼록 최적화를 사용하여 모든 조각을 함께 맞춘다.^[37]

비선형 PCA

비선형 PCA(NLPCA)는 백프로파게이션을 사용해 다층셉트론(MLP)을 다지관에 맞도록 훈련한다.^[38]가중치만 업데이트하는 일반적인 MLP 훈련과 달리 NLPCA는 가중치와 입력 모두를 업데이트한다.즉, 가중치와 입력 모두 잠재된 값으로 취급된다.훈련 후 잠재 입력은 관찰된 벡터의 저차원적 표현이며, MLP 맵은 그 저차원적 표현에서 고차원적 관측 공간에 이르는 것이다.

데이터 기반 고차원적 스케일링

Data-Driven 고등차원 Scaling(DD-HDS)[39]은 밀접하게 관련된 새몬의 매핑과 곡선 성분 분석는 것을 제외하면(1)동시에 제재를 잘못된 지역과 눈물에 의해 초점을 두고 짧은 거리에서 원래의 두 및 출력 공간, 그리고(2)이 차지하는의 집중력을 측정 현상에 적응하려면 시간이 무겁다.차랑거리다거리 분포에 따라 기능하다

다지관 조각

다지관 조각은^[40] 내장을 찾기 위해 절삭된 최적화를 사용한다.다른 알고리즘과 마찬가지로 가장 가까운 이웃을 계산하고 지역 이웃의 관계를 보존하는 임베딩을 모색한다.그것은 천천히 더 높은 차원의 분산을 스케일링하는 동시에 그러한 관계를 보존하기 위해 더 낮은 차원의 점을 조정한다.스케일링 비율이 작으면 매우 정밀한 임베딩도 찾을 수 있다.여러 문제가 있는 다른 알고리즘보다 높은 경험적 정확도를 자랑한다.또한 다른 다지관 학습 알고리즘의 결과를 세분화하는 데도 사용할 수 있다.그러나 매우 느린 스케일링 속도를 사용하지 않는 한 일부 다지관을 펼치는데 어려움을 겪고 있다.그것은 모델이 없다.

랭크비수

랭크비수는^[41] 거리보다는 동네의 순위를 보존하기 위해 고안된 것이다.랭크비수는 특히 어려운 작업(거리 보존이 만족스럽게 이루어질 수 없는 경우)에 유용하다.실제로 근교의 계급은 거리(거리에서는 계급이 추론될 수 있지만, 계급에서는 추론할 수 없음)보다 정보성이 떨어지고, 따라서 그 보존이 용이하다.

위상학적으로 제한된 등축 임베딩

TCIE(^[42]Topology Restricted Isometric Embedding, TCIE)는 유클리드 메트릭과 일치하지 않는 지오데틱을 필터링한 후 근사 지오데틱 거리에 기초한 알고리즘이다.Isomap을 사용하여 본질적으로 비콘벡스 데이터를 매핑할 때 발생하는 왜곡을 교정하기 위해 TCIE는 보다 정확한 매핑을 얻기 위해 중량 최소 제곱 MDS를 사용한다.TCIE 알고리즘은 먼저 데이터에서 가능한 경계점을 감지하고, 지오데틱 길이를 계산하는 동안 일치하지 않는 지오데틱을 표시하며, 이후 가중된 응력 전공화에 작은 가중치를 부여한다.

균일한 다지관 근사치 및 투영

균일한 다지관 근사 및 투영(UMAP)은 비선형 치수 감소 기법이다.^[43]시각적으로는 t-SNE와 비슷하지만, 데이터가 국지적으로 연결된 리만 다지관에 균일하게 분포하고 리만 메트릭스가 국지적으로 일정하거나 국지적으로 대략 일정하다고 가정한다.^[44]

근접 행렬에 기반한 방법

근접 행렬에 기초한 방법은 데이터가 유사 행렬 또는 거리 행렬의 형태로 알고리즘에 제시되는 방법이다.이 방법들은 모두 광범위한 미터법 다차원적 스케일링 등급에 속한다.이러한 변화는 근접 데이터를 계산하는 방법의 차이인 경향이 있다. 예를 들어, Isomap, 로컬 선형 임베딩, 최대 분산 전개, 그리고 Sammon 매핑(사실상 매핑이 아님)은 미터법 다차원 스케일링 방법의 예들이다.

참고 항목

• 다지관 가설
• 스펙트럼 하위매니폴드
• 테이크의 정리
• 휘트니 임베딩 정리
• 판별분석
• 탄성지도
• 피처러닝
• 자체 구성 맵(GSOM) 증가
• 자체조직지도(SOM)

참조

외부 링크

• 이소맵
• 생성 지형 매핑
• 마이크 티핑의 논문
• 가우스 공정 잠재 변수 모형
• 로컬 선형 임베딩
• 관계형 투시도
• 와플은 LLE, 다지관 조각 및 기타 일부 다지관 학습 알고리즘을 구현한 오픈 소스 C++ 라이브러리다.
• DD-HDS 홈페이지
• 랭크비수 홈페이지
• IMT2000 3GPP - 확산지도의 짧은 리뷰
• 자동인코더 신경망에 의한 비선형 PCA