제곱근 계산 방법

이 문서에는 여러 가지 문제가 있습니다.개선을 돕거나 토크 페이지에서 이러한 문제에 대해 논의해 주십시오.(이러한 템플릿메시지를 삭제하는 방법과 타이밍에 대해 설명합니다) 이 기사에는 독창적인 연구가 포함되어 있을 가능성이 있다. 클레임을 확인하고 인라인 인용을 추가하여 개선해 주십시오. 독창적인 연구로만 구성된 진술은 삭제되어야 한다.(2012년 1월) (이 템플릿메시지의 삭제 방법과 삭제 타이밍을 확인합니다) 이 기사는 대부분의 독자들이 이해하기에는 너무 전문적일 수 있다. 기술적인 세부사항을 삭제하지 않고 비전문가가 이해할 수 있도록 개선해 주세요.(2012년 9월) (이 템플릿메시지 삭제 방법 및 삭제 타이밍을 확인) 이 글은 검증을 위해 추가 인용문이 필요합니다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 기사를 개선하는 데 도움을 주십시오. 조달되지 않은 자재는 제거될 수 있습니다.출처 : '제곱근 계산법'– 뉴스 · 신문 · 서적 · 학자 · JSTOR (2017년 7월) (이 템플릿 메시지 삭제 방법 및 삭제 시기 확인) 이 글은 너무 길어서 쉽게 읽고 탐색할 수 없을 수도 있습니다.현재 읽을 수 있는 산문 크기는 61킬로바이트입니다. 콘텐츠를 소논문으로 분할하거나 압축하거나 소제목을 추가하는 것을 고려해 주십시오. 이 문제는 기사 토크 페이지에서 논의해 주십시오.(2019년 6월) (이 템플릿메시지를 삭제하는 방법과 타이밍을 확인합니다)

제곱근을 계산하는 방법은 주 제곱근(보통$$S\$displaystyle\sqrt {S$ $(\$를 근사하기 위한 수치 분석 알고리즘이다.$S$ $또는{\displaystyle {}^{}}$ ${\displaystyle {S\mathrm{}}^{}}$1/$({$ S$^{1/$2$\}\})$의 실수입니다.산술적으로 S$(\displaystyle$ S$)$를 구하면 S$(\displaystyle$ S$)$가 $되고{\displaystyle }$, 대수적으로 ${\displaystyle \mathrm{x2}{}^{}}$- S ${\displaystyle =}$(\$displaystyle$ x$^2}-S=0$의 음이 아닌 근을 구하는 절차를 의미하며, 기하학적으로 두 개의 세그먼트가 주어지는 것을 의미한다.기하 평균을 구성하는 절차입니다.

모든 실수는 두 제곱근을 ^{[Note 1]}가지고 있다.대부분의 숫자의 주 제곱근은 무한 소수 확장을 갖는 무리수입니다.그 결과, 이러한 제곱근의 십진수 팽창은 유한 정밀도 근사치까지만 계산할 수 있다.그러나, 우리가 완벽한 제곱 정수의 제곱근을 취해서 그 결과가 정확한 유한 표현을 가지도록 하더라도, 그것을 계산하는 데 사용되는 절차는 점점 더 정확한 일련의 근사치만 반환할 수 있습니다.

실수의 연속분수 표현은 소수 또는 2진수 확장 대신 사용될 수 있으며, 이 표현은 유리수의 제곱근(이미 완전한 제곱이 아님)이 소수 공터에서 반복 확장을 갖는 것과 유사한 주기적인 반복 확장을 갖는 특성을 가지고 있다.이온계

가장 일반적인 분석 방법은 반복적이며, 두 단계로 구성됩니다. 적절한 시작 값 찾기, 종료 기준이 충족될 때까지 반복적인 정교화입니다.시작 값은 임의의 수이지만 최종 결과에 가까울수록 반복 횟수가 줄어듭니다.프로그램 계산에 가장 적합한 가장 친숙한 방법은 미적분에서의 도함수의 특성에 기초한 뉴턴의 방법이다.종이와 연필로 된 합성 분할 및 직렬 확장과 같은 몇 가지 방법에서는 시작 값이 필요하지 않습니다.응용 프로그램에 따라서는 가장 가까운 정수로 반올림되거나 잘린 제곱근인 정수 제곱근이 필요합니다(이 경우 수정된 절차를 사용할 수 있습니다).

사용되는 방법은 어떤 결과에 사용할 것인가(즉, 얼마나 정확해야 하는가), 절차에 얼마나 많은 노력을 기울일 것인가, 그리고 수중에 있는 도구에 따라 달라집니다.이 방법들은 대략적으로 정신적 계산에 적합한 방법, 보통 최소한 종이와 연필을 필요로 하는 방법, 그리고 디지털 전자 컴퓨터나 다른 컴퓨팅 장치에서 실행되는 프로그램으로 구현되는 방법들로 분류될 수 있다.알고리즘은 수렴(특정 정밀도를 달성하기 위해 몇 번의 반복이 필요한지), 개별 연산의 계산 복잡성(즉, 나눗셈) 및 오류 전파(최종 결과의 정확도)를 고려할 수 있다.

제곱근(특히 2의 제곱근)을 찾는 절차는 적어도 기원전 17세기 고대 바빌론 시대부터 알려져 왔다.1세기 이집트 헤론의 방법은 제곱근을 계산하는 최초의 확인 가능한 알고리즘이었다.현대 분석법은 르네상스 초기 서유럽에 아랍어 숫자 체계가 도입된 이후 개발되기 시작했다.오늘날 거의 모든 컴퓨팅 디바이스는 프로그래밍 언어 구성, 컴파일러 고유 함수 또는 라이브러리 함수 또는 하드웨어 오퍼레이터로서 기술된 절차 중 하나에 따라 빠르고 정확한 제곱근 함수를 가지고 있습니다.

초기 견적

많은 반복 제곱근 알고리즘에서는 초기 시드 값이 필요합니다.시드는 0이 아닌 양수여야 합니다.이 값은 1 ~$S($$제곱$ 루트가 필요한 수)여야 합니다.제곱 루트는 이 범위 내에 있어야 합니다.시드가 루트에서 멀리 떨어져 있는 경우 알고리즘에 더 많은 반복이 필요합니다.${\displaystyle {x\mathrm{}}_{}}$ 0 $=$ ${\displaystyle 1}${$displaystyle x_{0$}=$1}($$또는{\displaystyle }$S {\$displaystyle$S})$$로 초기화할 경우 약 ${\displaystyle 1_{}{}_{}}$ ${\displaystyle \frac{2}{}}$ ${\displaystyle \mathrm{로그2}{}_{}}$s$$S(\$displaystyle {1}{2}}\vert \log$ _${2}S\vert})$의 반복은 루트의 크기 순서만 얻어도 낭비됩니다.따라서 정확도가 제한적일 수 있지만 계산하기 쉬운 대략적인 추정치를 갖는 것이 유용합니다.일반적으로 초기 추정치가 좋을수록 수렴 속도가 빨라집니다.뉴턴의 방법(바빌로니아식 또는 헤론식이라고도 함)에서, 뿌리보다 약간 큰 씨앗은 뿌리보다 약간 작은 씨앗보다 약간 더 빨리 수렴할 것입니다.

일반적으로 견적은 루트를 포함하는 것으로 알려진 임의의 간격(${\displaystyle {}_{}}:{\displaystyle }$ [ ${\displaystyle {x\mathrm{}}_{}}$0 ,${\displaystyle S{}_{}}$ / x $]$ { $displaystyle$[$x$_ {$0$ ,$S$ / x$_$ { $0$} $$)에 따릅니다.추정치는 간격 동안${\displaystyle }$f(${\displaystyle x)}$ $=$ {\$displaystyle$ f$(x$)=$sqrt {x}}$에 $대한{\displaystyle }$ 함수 근사치의 특정 값이다.더 나은 추정치를 얻으려면 간격에 대한 더 엄격한 경계를 얻거나 f${\displaystyle }$(${\displaystyle x}$ $)\style$ f$(x$에 $대한{\displaystyle }$ 더 나은 함수 근사치를 구해야 합니다.후자는 모든 근사가 다항식인 것은 아니지만 근사치에 고차 다항식을 사용하는 것을 의미한다.일반적인 추정 방법에는 스칼라, 선형, 쌍곡선 및 로그가 있습니다.십진법은 보통 정신적 또는 종이와 연필로 추정할 때 사용됩니다.바이너리 베이스가 컴퓨터 견적에 더 적합합니다.추정을 할 때, 그 숫자는 과학적인 표기법으로 표현될 것이기 때문에, 지수와 가수수는 보통 따로 취급된다.

십진수 추정치

일반적으로 번호 S{S\displaystyle}과학적 기수 법에서 x102n{\displaystyle a\times 10^{2n}로}1≤<>100{\displaystyle 1\leq a<, 100}과 n는 정수, 제곱 근의 범위 내에 있는×10n{\displaystyle{\sqrt{}표시된다}}1≤ a10^{n}\times <>10$(\displaystyle$ 1$\leq\displayrt {a}}<10$

스칼라 추정치

스칼라 메서드는 범위를 구간으로 나누고 각 간격의 추정치는 단일 스칼라 번호로 나타냅니다.범위를 단일 구간으로 간주할 경우 산술 평균(5.5) 또는 기하 평균(${\displaystyle \sqrt{10}3}$3.$16(\sqrt {10$ ${\displaystyle {\mathrm{x}}^{}}$ $(\$ 10$^{n})$은 타당한 추정치입니다.이들 에러의 절대오차와 상대오차는 다릅니다.일반적으로 단일 스칼라는 매우 부정확합니다.더 나은 추정치는 범위를 두 개 이상의 구간으로 나누지만 스칼라 추정치는 본질적으로 정확도가 낮습니다.

기하학적으로 나누면 $제곱근{\displaystyle \sqrt{}}$ S $=$ ${\displaystyle a\sqrt{}}$ × ${\displaystyle {10}^{}}$n$displaystyle {S$}}=$sqrt {a}}\times$ 10$^{n})$은 다음과 같이 추정할^{[Note 2]} 수 있다.

${\displaystyle {sqrt {S}\cdot 10^{n}&{\text{if}}a<10,\6\cdot 10^{n}&{\text{if}}}a\geq 10.\end {case}}$

이 추정치의 최대 절대 오차는 a ${\displaystyle =}$ 100에서 ${\displaystyle {4\mu 10}^{}}$ n$(\$ 4$\cdot$ 10$^{n})$이며, 최대 상대 오차는 a = 1에서 100%이다.

예를 들어 S${\displaystyle \mathrm{}=}$ ${\displaystyle 12}$$.$$5348$× ${\displaystyle {10}^{}}$4 {{$displaystyle 12.5348$인 $경우$, $추정치$는 S${\displaystyle 0}$ 6$$ 10 ${\displaystyle 2}$ $=$ 600 {\${\displaystyle \mathrm{displaystyle}}$$10 ^$ {2} $=$ $600$$= 12$.$=$ ${\displaystyle 354}$거의 70%의 확률입니다.

선형 추정치

더 나은 추정치 및 사용되는 표준 방법은 작은 호에서 $함수{\displaystyle }$ y ${\displaystyle =}$ ${\displaystyle {}^{}}$ $(\$ y$=x^{2})$에 선형 근사하는 것입니다.위와 같이 베이스의 파워를 $S$에서 인수하여 ${\displaystyle \mathrm{간격}}$을${\displaystyle }$[${\displaystyle 1,}$ 100$]({displaystyle [1,$100$])$로 줄이면 호를 가로지르는 분할선 또는 호를 따라 접선선을 근사치로 사용할 수 있지만 호를 교차하는 최소 제곱 회귀선을 보다 정확하게 사용할 수 있습니다.먹었다.

최소 제곱 회귀선은 추정치와 함수 값 사이의 평균 차이를 최소화합니다.$방정식$은 y ${\displaystyle =8.7x}$ - $({displaystyle$ y$=8.7x-10$ 정렬, $x{\displaystyle }$ ${\displaystyle =0}$.${\displaystyle \mathrm{115}}$y +$({display$ x$=0.115y+1.$15$\})$입니다.계수를 반올림하여 쉽게 계산할 수 있습니다.

$\ displaystyle \ sqrt { S } \ about ( a / 10 + 1.2 ) \ cdot 10 ^ { n }$

이는${\displaystyle }$[${\displaystyle 1,}$ $]({displaystyle [1,100$ 구간에서 y=x² 함수의 단일 조각 선형 근사치로 얻을 수 있는 평균 추정치입니다.a=100에서 최대 절대 오차가 1.2이고, S=1 ^{[Note 3]}및 10에서 최대 상대 오차가 30%이다.

10으로 나누려면$$\$displaystyle$a의 $지수$에서 1을 빼거나 소수점을 왼쪽으로 한 자리 이동합니다.이 공식의 경우, 가법 상수 1에 작은 증분을 더하면 만족스러운 추정을 할 수 있으므로 정확한 숫자를 기억하는 것은 부담이 되지 않습니다.범위${\displaystyle }$[${\displaystyle 1,}$ $]$ {$displaystyle [1$,100$]$ {displaystyle [1$,100$]} 의$$ 1 개의 선을 사용한 근사치(반올림 여부)는 유의한 정밀도 1 자리 미만이며 상대 오차는 1/2² 이므로 2 비트 미만의 정보가 제공됩니다.범위가 2차 크기이기 때문에 정확도가 심각하게 제한됩니다. 이러한 종류의 추정치로는 상당히 큽니다.

훨씬 더 나은 추정치는 조각별 선형 근사치, 즉 각각 원본의 하위 호에 가까운 여러 선분을 통해 얻을 수 있습니다.사용되는 선분이 많을수록 근사치가 향상됩니다.가장 일반적인 방법은 접선을 사용하는 것입니다. 중요한 선택은 호를 분할하는 방법과 접선을 배치하는 위치입니다.y=1에서 y=100으로 호를 나누는 효과적인 방법은 기하학적으로 두 구간에서 구간의 경계가 원래 구간 경계의 제곱근인 1*100, 즉 ²[1,4100,100]과 ²[1,4100,100]이 됩니다.3개의 간격 동안 경계는 100의 세제곱근 [1, ³µ100],³ [,100,³ ()²100),³ 100]² 등입니다.두 간격 동안, 100100 = 10은 매우 편리한 숫자입니다.접선은 도출이 용이하며 x = √1*1010 및 x = √10*1010에 위치합니다.방정식은 y ${\displaystyle =}$ ${\displaystyle 3.\mathrm{56}}$x -$({displaystyle y=3.56x-3.$$16$} 및 y =${\displaystyle \mathrm{11}}$.2${\displaystyle \mathrm{x}}$- ${\displaystyle 31}$.6({$displaystyle$ y$=11.2x-31.6$입니다. 반대로 제곱근은 다음과 $같습니다{\displaystyle }$.${\displaystyle \mathrm{x}}$ ${\displaystyle =}$ 0.${\displaystyle \mathrm{28}}$ ${\displaystyle \mathrm{y}}$ +${\displaystyle 0}$.89$(style$ x$=$$0$.6$)$$28y+0.89$및$$ $x{\displaystyle }$ $=$ 0.${\displaystyle \mathrm{089y}}$+ 2$(디스플레이 스타일x$=.$089y+$$2$)$8{\displaystyle }$$\}.$ 따라서 S ${\displaystyle =}$ ${\displaystyle a{10}^{}}$ ${\displaystyle {10\mathrm{}}^{}}$ ${\displaystyle 2^{}}$n { $displaystyle$ S $= a$ \ $cdot$ 10^ { 2 $n$} :

${\displaystyle {sqrt {S}\cdot 10^{n}&{\text{if}}a < 10,\(.089a+2.8)\cdot 10^{n}&{text{if}a}\geq 10.\end {case}}$

최대 절대 오차는 a=10과 100의 구간 고점에서 발생하며 각각 0.54와 1.7입니다.최대 상대 오차는 구간의 끝점인 a=1, 10, 100에 있으며 두 경우 모두 17%입니다.17%(0.17)는 1/10보다 크므로 이 방법은 정확도가 소수점 이하입니다.

쌍곡선 추정치

어떤 경우에는 쌍곡선 추정치가 효과적일 수 있는데, 쌍곡선² 역시 볼록 곡선이고 선보다 Y = x의 호를 따라 있을 수 있기 때문입니다.쌍곡선 추정치는 반드시 부동 분할이 필요하기 때문에 계산이 더 복잡합니다.구간${\displaystyle }$[${\displaystyle 1}$,$]$ {$displaystyle [1$,100$]$ {displaystyle [1$,100$]}의$$ x에 대한 거의² 최적의 쌍곡선 근사치는 y=sq0/(10-x)-20입니다.치환하면, 제곱근은 x = -sq/(y+20)+10입니다.따라서 S ${\displaystyle =}$ ${\displaystyle a{10}^{}}$ ${\displaystyle {\mathrm{102n}}^{}}${\$displaystyle$ S$=a\cdot$ 10$^{2n$의 $경우{\displaystyle }$:

${\displaystyle {sqrt {S}}\약 왼쪽({\frac {-190}{a+20}}+10\오른쪽)\cdot 10^{n}$

플로팅 나눗셈은 소수점 이하 한 자리까지만 정확해야 합니다. 왜냐하면 전체 추정치가 정확하고 정신적으로도 정확하기 때문입니다.쌍곡선 추정치는 스칼라 또는 선형 추정치보다 평균적으로 더 좋습니다.100에서 최대 절대 오차는 1.58이고 10에서 최대 상대 오차는 16.0%입니다.a=10인 최악의 경우 추정치는 3.67입니다.10부터 시작하여 뉴턴-라프슨 반복을 즉시 적용하면 쌍곡 추정의 정확도가 초과되기 전에 3.66을 산출하는 두 번의 반복이 필요합니다.75와 같은 보다 일반적인 경우, 쌍곡선 추정치는 8.00이며, 보다 정확한 결과를 얻으려면 75에서 시작하는 5번의 뉴턴-라프슨 반복이 필요합니다.

산술적 추정치

대수 방정식 대신 산술만 사용하는 조각 선형 근사법과 유사한 방법은 곱셈표를 반대로 사용한다. 1과 100 사이의 숫자의 제곱근은 1과 10 사이이므로 25가 완벽한 제곱근(5 × 5), 36이 완벽한 제곱근(6 × 6), 그리고 더 큰 숫자의 제곱근이다.25에서 36보다 작을 경우 5로 시작합니다.다른 정사각형 사이의 숫자도 비슷합니다.이 방법을 사용하면 첫 번째 숫자는 정확하지만 한 자리에는 정확하지 않습니다.예를 들어 35의 제곱근의 첫 번째 숫자는 5이지만 35의 제곱근은 거의 6입니다.

더 나은 방법은 범위를 정사각형 사이의 중간 구간으로 나누는 것입니다.즉, 25에서 36까지의 반수(30.5)는 5로 추정되고, 30.5에서 36까지의 숫자는 ^{[Note 4]}6으로 추정됩니다.이 절차에서는 곱셈표에서 두 곱의 중간에 있는 경계 번호를 찾기 위해 약간의 산술만 필요합니다.다음은 이러한 경계에 대한 참조 표입니다.

a	가장 가까운 정사각형	${\displaystyle k\sqrt{}}$ ${\displaystyle =}$\ $displaystyle$ k =$estrt {a}$ est$$.
1 ~ 2.5	1(= 12)	1
2.5 ~ 6.5	4(= 22)	2
6.5 ~ 12.5	9(= 32)	3
12.5 ~ 20.5	16(= 42)	4
20.5 ~ 30.5	25(= 52)	5
30.5 ~ 42.5	36(= 62)	6
42.5 ~ 56.5	49(= 72)	7
56.5 ~ 72.5	64(= 82)	8
72.5 ~ 90.5	81(= 92)	9
90.5 ~ 100	100 (= 102)	10

최종 연산은 추정치 k에 10 나누기 2를 곱하는 것으로, S ${\displaystyle =}$ ${\displaystyle a{10}^{}}$ ${\displaystyle {10\mathrm{}}^{}}$ 2$$ \ $displaystyle$ S $= a$ \ $cdot$ 10$^{2n$의 $경우{\displaystyle }$,

$(\displaystyle\sqrt {S}\about k\cdot 10^{n})$

이 메서드는 암묵적으로 가장 좋은 첫 자릿수로 반올림하기 때문에 한 자릿수의 정확도를 산출합니다.

이 방법은 대부분의 경우 피연산자 경계에 있는 가장 가까운 정사각형 사이에 보간하여 유효 자릿수를 3자리까지 확장할 수 있습니다. 2< (k + ) {{ $displaystyle$ k$^{2}$ \$leq$ a < ( k +$1$)^{$2$인 $,$ \ $displaystyle${ $sqrt {a}}}$는 약 k + 분수로, a와² k의 차이를 두 제곱의 차이로 나눈 값입니다.

${\displaystyle \sqrt{a}\mu }$k $+$ ($여기$서 R$$${\displaystyle =\frac{}{}}$ (${\displaystyle \frac{a}{}}$ - ${\displaystyle \frac{{}^{}{2\mathrm{}}^{}}{}}$) (${\displaystyle \frac{{k\mathrm{}}^{}}{}}$ +${\displaystyle \frac{{}^{}1}{}}$)${\displaystyle \frac{{}^{}{}^{}}{}}$ - ${\displaystyle \frac{{k\mathrm{}}^{}}{}}$2 ( \ $display R$$$$= scfrac${ ( a - k$^{2$} ) { ($k$ + $1)^{2}$ - $k^{2}}}}$

마지막 연산은 위와 같이 결과를 10 나누기 2로 곱하는 것이다.

$({displaystyle {S}}=sqrt {a}}\cdot 10^{n}\approx (k+R)\cdot 10^{n})$

k는 십진수, R은 십진수로 변환해야 하는 분수입니다.보통 분자에 한 자리, 분모에 한 자리 또는 두 자리만 있기 때문에 10진수로 변환할 수 있습니다.

예: 75의 제곱근을 구하십시오. 75 = 75 × 10^{2 · 0}. 따라서 a는 75이고 n은 0입니다.곱셈표에서 사수의 제곱근은 8 × 8은 64이므로 8점 뭔가여야 하지만, 9 × 9는 81로 너무 커서 k는 8이고, 무엇인가는 R의 십진수 표현이다.분수 R은 분자인 75² - k = 11이고 분모인 81 - k² = 17입니다. 11/17은 12/18보다 조금 작아서 2/3s 또는 .67입니다. 따라서 .66을 추측해 보십시오(여기서는 오차가 매우 작습니다).따라서 추정치는 8 +.66 = 8.66입니다. 7575 ~ 3개의 유효 자릿수는 8.66이므로 3개의 유효 자릿수로도 괜찮습니다.이 방법을 사용하는 모든 추정치가 정확하지는 않지만 비슷할 것입니다.

이항 추정치

언제의 이진법 숫자 시스템(컴퓨터 내부적으로니)에×22n{\displaystyle a\times 2^{2n}로}이 0.12<>≤ 102{0.1_{2\displaystyle}\leq a< S{S\displaystyle}을 발표하여;10_{2}}, 제곱 근 S)×2n{\displaystyle{\sqrt{S}}={\sqrt{}}}2^{n}\times고요.할 수 있다로 추정되다

$\ displaystyle \ sqrt { S } \ about ( 0 . 485 + 0 . 485 \ cdot a ) \ cdot 2 ^ { n }$

유효 자릿수 계수에 대한 최소 회귀선입니다.${\displaystyle \sqrt{}}${\$displaystyle {a}}$은$($는) {$displaystyle$ a$}$$2$에서 최대 절대 오차가 0.0408이고 {\$displaystyle$ a$}$$1$에서 최대 상대 오차가 3.0%입니다.계산상 편리한 반올림 추정치는 다음과 같습니다(계수가 2의 거듭제곱이므로).

$(\displaystyle\sqrt {S}}\약 (0.5+0.5\cdot a)\cdot 2^{n})$^{[주 5]}

이 값은 2에서 최대 절대 오차가 0.086이고 {\$displaystyle$ a$}$ 0.5 $및{\displaystyle }$ {\$display$ a$}$ 2.0에서 $최대{\displaystyle }$ 상대 오차가 6.1%입니다.

$S{\displaystyle }$ ${\displaystyle =}$ ${\displaystyle 125348}$ ${\displaystyle =}$ ${\displaystyle 1}$ ${\displaystyle 1110}$ ${\displaystyle 1001}$ ${\displaystyle 1010}$ ${\displaystyle {0100\mathrm{}}_{}}$ 2${\displaystyle {}_{}{}_{}1}$ . ${\displaystyle 1110}$ ${\displaystyle 1001}$ ${\displaystyle {10100\mathrm{}}_{}}$ 2 × ${\displaystyle 2^{}}$ 16 ${\displaystyle ({}^{}}$ { $displaystyle$ S =$125348$=$1$\ ; $1110$\ ; $1001$\ ; $1010 _$ { 2 } =$$1 . 1110 \ ; 1001 \ ; $10$\ $10$ \ $0100$_ 2 }$、$ { $16$ $\}$ $times$${\displaystyle {S}\apprough (0.5+0.5\cdot a)\cdot 2^{8$$=1$$.$0111$\;0100\;1101\;cdot 1\;0000$\;$00_${2}=1.456\cdot $256$${\displaystyle =}$$2.8.$${\displaystyle \sqrt{1254}}$\cdot $\style$상대 오차는 1/2보다⁴ 조금 작기 때문에 추정치는 4비트 이상입니다.

$style$$a$의$$상위8비트를 $표$로 검색하면 알 수 있습니다.상위8비트는 대부분의 부동소수점 표현에서 암묵적으로 나타나므로 8비트의 하단비트는 반올림해야 합니다.테이블은 사전 계산된8비트 제곱근 값 256바이트입니다.예를 들어 1.8515625를₁₀ 나타내는 인덱스 11101101의₂ 경우 엔트리는 1.359375를₁₀ 나타내는 10101110으로₂ 1.8515625₁₀~8비트 정밀도(2+10진수)의 제곱근입니다.

바빌로니아법

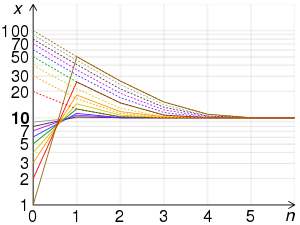
아마도 S$(\$의 근사화에 사용된 최초의 알고리즘은 바빌로니아 방법이라고 알려져 있을 것이다.그러나 바빌로니아 수학자들이 ^[1]이 방법을 사용했다는 확실한 추측 외에는 증거가 없다.이 방법은 1세기 그리스 수학자 알렉산드리아의 영웅의 이름을 따서 헤론의 방법이라고도 알려져 있는데, 그는 서기 60년 그의 작품 메트릭카에서 ^[2]이 방법을 처음으로 명확하게 기술했다.그 기본적인 생각은 if)는non-negative 실제 번호 S의 제곱 근에 과대 평가하다 그러면 .mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output.sfrac.tion,.mw-parser-output.sfrac .tion{디스플레이:inline-block, vertical-align:-0.5em, font-size:85%;text-align:센터}.mw-parser-output.sfrac .num,.mw-parser-output.sfrac .den{다.디스플레이:블록, line-height:1em, 마진:00.1em}.mw-parser-output.sfrac .den{border-top:1px 고체}.mw-parser-output .sr-only{국경:0;클립:rect(0,0,0,0), 높이:1px, 마진:-1px, 오버 플로: 숨어 있었다. 패딩:0;위치:절대, 너비:1px}S/x 과소 평가되어 진 또는 그 반대로 이 두 숫자의 평균 합리적으로 제공할 것으로 예상될 수 있다.더 좋은 근사(비록 그 주장의 형식적인 증거와 기하 평균 수준의 불평등에 달려 있다.ns는 제곱근에 관한 기사에서 설명한 바와 같이 이 평균은 제곱근의 과대평가이므로 수렴이 보증됩니다).이는 뉴턴의 방법을 사용하여 ${\displaystyle {x\mathrm{}}^{}}$2 - ${\displaystyle S}$ ${\displaystyle =}$ {\$displaystyle$ x$^{2}-S=0$을(를) 푸는 것과 같습니다.

보다 정확하게는 x가$S$의 $초기{\displaystyle \sqrt{}}$ $추정치이고,$ε가 S$$= (x+ ),)²와 같은 추정치의 오차라면, 우리는 이항식을 확장하여 해결할 수 있다.

${\displaystyle \epsilon \frac{}{}}$= ${\displaystyle \frac{{}^{}}{}}$- ${\displaystyle \frac{x}{}}$ 2${\displaystyle \frac{}{}}$x +$s$ ${\displaystyle \frac{{}^{}}{}}$- ${\displaystyle \frac{{}^{}}{\mathrm{}}}$ ${\displaystyle \frac{2}{}}$x , {$displaystyle$ \ varepsilon $= specfrac$ { S - x ^ { $2$} { 2x + \ $varepsilon$$}$${\displaystyle \mathrm{\epsilon <img\; alt="\{\backslash displaystyle\; \backslash varepsilon\; =\{\backslash frac\; \{S-x^\{2\}\}\{2x+\backslash varepsilon\; \}\}\backslash approx\; \{\backslash frac\; \{S-x^\{2\}\}\{2x\}\},\}"\; aria-hidden="true"\; class="mwe-math-fallback-image-inline"\; src="https://wikimedia.org/api/rest\_v1/media/math/render/svg/172688bcc66ae99132d463bcfcaf67ef710dda68"\; style="vertical-align:\; -2.005ex;\; width:23.047ex;\; height:5.843ex;">}}$ {\$$≪ {\ {\ {\ {\ {\ $x$ \$frac$ { S - x$$^ {$2$ $\}$ {\ 、 \ $frac$ { S - ${\displaystyle \frac{{x\mathrm{}}^{}}{}}$$$2 } } $。$

따라서 오류를 보완하고 이전 견적을 다음과 같이 갱신할 수 있습니다.

${\displaystyle x+\varepsilon \approx+{\frac {S-x^{2}}{2x}=black {S+x^{2x}}{2}=black {\frac {S}{x}+x}{2}}}\equiv x_{\text {filename}}$

계산된 오차가 정확하지 않았기 때문에 이것이 차선책이 됩니다.원하는 정확도를 얻을 때까지 업데이트 프로세스를 반복합니다.이것은 2차적으로 수렴하는 알고리즘입니다.즉, 각 반복에 따라 대략적인 자릿수가 약 2배가 됩니다.다음과 같이 진행됩니다.

1. 임의의 양의 시작 값₀ x로 시작합니다(실제 S의 제곱근에 가까울수록 좋습니다).
2. x를 x와 S/x의_n 평균으로_n 합니다_{n + 1}(산술 평균을 사용하여 기하 평균에 근사함).
3. 원하는 정확도에 도달할 때까지 2단계를 반복합니다.

다음과 같이 나타낼 수도 있습니다.

${\displaystyle x_{0}\약 {\sqrt {S}}$

$({displaystyle x_{n+1}=snfrac {1}{2}}\left(x_{n}+{\frac {S}{x_{n}}\right})})$

${\displaystyle {\displaystyle {S}}=\lim _{n\to\infty}x_{n}.}$

이 알고리즘은 p-adic 수에서는 동일하게 동작하지만, p-adic 제곱근으로 실수 제곱근을 식별하는 데 사용할 수 없습니다. 예를 들어, 이 방법을 사용하면 실수에서는 +3으로 수렴하지만 2-adic에서는 -3으로 수렴하는 유리수의 시퀀스를 구성할 수 있습니다.

예

S = 125348인 µS를 6개의 유효 수치로 계산하려면 위의 대략적인 추정 방법을 사용하여 다음을 구하십시오.

${\displaystyle{\begin{정렬}{\begin{배열}{rlll}x_{0}&, =6\cdot 10^{2}&,&=600.000\\[0.3em]x_{1}&, ={\frac{1}{2}}\left(x_{0}+{\frac{S}{x_{0}}}\right)&, ={\frac{1}{2}}\left(600.000+{\frac{125348}{600.000}}\right)&, =404.457\\[0.3em]x_{2}&, ={\frac{1}{2}}\left(x_{1}+{\frac{S}{x_{1}}}\right)&, ={\frac{1}{2}}\left(404.457+{년.frac{125348}{404.457}}\right)&=357.199\\[0.3em]x_{3}&=flac {1}{2}}\left(x_{2}+{\flac {S}{x_{2}}\right)&=flac {1}{2}\left(357.flac {125348}{357.flac}\right)&=354.059\03em{x}{x}{}\right}.}&=flac {1}{2}}\left(x_{3}+{\flac {S}{x_{3}}\right)&=flac {1}{2}\left(354.059+{354.05}\right)&=354.045\[03]em{}\right}.$

따라서 '125348' 354.045 입니다.

컨버전스

x > 0 및 S > 0이라고₀ 가정합니다.다음으로 임의의 자연수 n에 대해_n x > 0 입니다.x의 상대_n 오차는 다음과 같이 정의한다.

${\displaystyle \varepsilon _{n}=parecfrac {x_{n}}{\parecrt {S}}-1>-1}$

그래서

${\displaystyle x_{n}=cdot {S}}\cdot (1+\varepsilon _{n}).}$

그러면 알 수 있다

${\displaystyle \varepsilon _{n+1}=parecfrac {varepsilon _{n}{2}}{2(1+\varepsilon _{n}}}\geq 0.}$

그래서...

$\displaystyle \varepsilon _{n+2}\leq \min \left\{\frac {varepsilon _{n+1}^{2}, {\frac {varepsilon _{n+1}}{2}}\right\}$

그 결과 수렴이 보장되고 2차적으로 이루어집니다.

컨버전스 최악의 경우

위의 대략적인 추정치를 바빌로니아법으로 사용할 경우, 오름차순으로 가장 정확도가 낮은 경우는 다음과 같다.

$디스플레이 스타일S&=1;&x_{0}&=2;&x_{1}&=1.250;&\varepsilon_{1}&=0.250.\\S&=10;&x_{0}&=2;&x_{1}&=3.500;&\varepsilon_{1}&<0.199.\\S&=10;&x_{0}&=6;&x_{1}&=3.833;&\varepsilon_{1}&<0.213.\\S&=100;&x_{0}&=6;&x_{1}&=11.333;&\varepsilon_{1}&<0.134.\end { aligned}}$

따라서 어떤 경우에도,

$\displaystyle \varepsilon _{1}\leq 2^{-2},$

${\displaystyle \varepsilon _{2}<2^{-5}<10^{-1}},$

$\displaystyle \varepsilon _{3} <2^{-111} <10^{-3},}$

${\displaystyle \varepsilon _{4} <2^{-23) <10^{-6},}$

${\displaystyle \varepsilon _{5}<2^{-47}<10^{-14}},$

${\displaystyle \varepsilon _{6}<2^{-95}<10^{-28}},$

${\displaystyle \varepsilon _{7}<2^{-191}<10^{-57}},}$

${\displaystyle \varepsilon _{8} <2^{-383} <10^{-115},}$

반올림 에러는 컨버전스의 속도를 늦춥니다.반올림 오류를 최소화하기 위해 계산 중인_n x의 원하는 정확도보다 적어도 한 자리 이상의 숫자를 유지하는 것이 좋습니다.

바크샬리법

제곱근에 대한 근사치를 찾는 이 방법은 박샬리 필사본이라고 불리는 파키스탄의 고대 남아시아 필사본에 묘사되었다.이는₀ 바빌로니아법을 x로 시작하는 두 번의 반복과 같습니다.따라서 알고리즘은 4차적으로 수렴됩니다.즉,^[3] 각 반복에 따라 대략적인 자릿수가 약 4배가 됩니다.현대 표기법을 사용한 원래의 프레젠테이션은 다음과 같습니다.S$(\$를 $계산$하려면 ${\displaystyle {x\mathrm{}}_{}^{}}$ $(\$를 S$(\displaystyle$ S$)$에 대한 초기 근사값으로 $합니다{\displaystyle {}_{}^{}}$. 그런 다음 다음과 같이 반복하십시오.

${\displaystyle {syslog{aligned}a_{n}&=frac {S-x_{n}^{2}}{2x_{n}},\x_{n}+a_{n},\x_{n}-{n}-{\frac {n}_{n}_{n}}{b}}}{x}}}\end { aligned}}$

이를 사용하여 정수로 시작하여 제곱근에 대한 합리적인 근사치를 구성할 수 있습니다.${\displaystyle {x\mathrm{}}_{}}$ 0 $=$ ${\displaystyle x_{$0$$}=N}이(가) $선택$된 정수이므로 N$$2 {\$displaystyle$N$^{2}}$이(가)$$S${\displaystyle <img\; alt="S"\; aria-hidden="true"\; class="mwe-math-fallback-image-inline"\; src="https://wikimedia.org/api/rest\_v1/media/math/render/svg/4611d85173cd3b508e67077d4a1252c9c05abca2"\; style="vertical-align:\; -0.338ex;\; width:1.499ex;\; height:2.176ex;">}${\${\displaystyle {}^{}}$ $=$S-N^{2}}에 $가깝고$ d =$S$- N 2 {$displaystyle$ d= S-N^2}}의$$ 절대값이 최소화된 차이일 경우 첫 번째 $반복$은 다음과 같이 기술할 수 있습니다.

${\displaystyle {sqrt {S}}\about N+{\frac {d}{2N}}-{\frac {d^{2}}{8}N^{3}+4Nd}}=sq frac {8N^{4}+8N^{2}d+d^{2}}}{8N^{3}+4Nd}}=blac{N^{4}+6N^{2}}S+S^{2}}}{4N^{3}+4NS}}=nfrac {N^{2}(N^{2}+6S)+S^{2}}{4N(N^{2}+S)}}.}$

Bakhshali 방법은 분수 ^[4]루트를 포함한 임의의 루트의 계산으로 일반화할 수 있습니다.

예

바빌로니아 방법과 동일한 예를 사용하여 S ${\displaystyle =}$ ${\displaystyle \mathrm{125348로}}$$하자{\displaystyle }$.$(\displaystyle S=125348).$$}$ 그러면$$ 첫 번째 반복은

$({displaystyle {displaystyle}x_{0}&=600\a_{1}&=frac {125348-600^{2}}{2\times 600}&=600+(-140.543)&=404.456\x_{1}&=frac {4}{}).$

마찬가지로 두 번째 반복은 다음을 제공합니다.

$({displaystyle {displaystyle}a_{2}&=frac {125348-357.display^{2}&=-3.displays\b_{2}&=357.displaystyle+(-3.display)&=354.060\x_{2}&=354-frac{}).$

자릿수 계산

이것은 일련의 제곱근의 각 자릿수를 찾는 방법입니다.바빌로니아식 방법보다 느리지만 다음과 같은 장점이 있습니다.

• 수동 계산이 더 쉬워질 수 있습니다.
• 발견된 루트의 모든 자릿수는 올바른 것으로 알려져 있습니다. 즉, 나중에 변경할 필요가 없습니다.
• 제곱근에 끝의 확장이 있는 경우 알고리즘은 마지막 숫자가 발견된 후 종료됩니다.따라서 주어진 정수가 정사각형 숫자인지 여부를 확인하는 데 사용할 수 있습니다.
• 알고리즘은 모든 베이스에서 동작하며, 당연히 선택한 베이스에 따라 처리 방법이 달라집니다.

네이피어의 뼈에는 이 알고리즘을 실행하는 데 도움이 되는 것이 포함되어 있다.시프트 n번째 루트 알고리즘은 이 방법의 일반화입니다.

기본원칙

먼저 숫자 Z의 제곱근, 즉 두 자리 숫자 XY의 제곱근을 찾는 경우를 생각해 보겠습니다. 여기서 X는 10자리 숫자이고 Y는 단위 숫자입니다.구체적으로는:

${\displaystyle Z=(10X+Y)^{2}=100X^{2}+20XY+Y^{2}}$

먼저 디지트 바이 디지트알고리즘을 사용하여 X의 값을 결정합니다.X는 가장 큰 디지트이며 X가² 가장 오른쪽 디지트를 삭제한Z 이하여야 합니다.

다음 반복에서는 숫자를 조합하고 X에 2를 곱한 다음 Y의 값을 구하는 동안 10번째 자리에 배치합니다.

이는 답이 완벽한 제곱근 XY인 단순한 경우이므로 알고리즘은 여기서 끝납니다.

다음에 같은 아이디어를 임의의 제곱근 계산으로 확장할 수 있습니다.N의 제곱근을 다음과 같이 n개의 양의 합으로 표현함으로써 구할 수 있다고 가정하자.

${{displaystyle N=(a_{1}+a_{2}+a_{3}+\dotsb+a_{n}^2}.}$

기본 아이덴티티를 반복적으로 적용함으로써

${\displaystyle(x+y)^{2}=x^{2}+2xy+y^{2}}$

오른쪽 항은 다음과 같이 확장될 수 있다.

${{displaystyle {argented}&(a_{1}+a_{3}+\displayb +a_{n})^{2}\=^{1}+2a_{1}a_{2}+a_{2}+a_{2}}^{2}+2(a_{1}+a_{2})a_{3}+a_{3}}^{2}+\sumb +a_{n-1}^{2}+2\left(\sum _ {i=1}^{n-1}a_{i}\right)a_{n}+a_{2}+{a_{1}+{2}_{2a}_2}_2}_2}_2_{a}\end { aligned}}$

이 식을 사용하면 i$\$의 $값$을 순차적으로 추측하여 제곱근을 구할 수 있습니다.$,$ ${\displaystyle {a-1}_{}}$({$displaystyle a_{1},\ldots,a_{m-1})$의 숫자가 이미 추측되었다고 가정하면, 위의 합계의 오른쪽의 m번째 항은 ${\displaystyle Y_{}}$ m $=$ [ ${\displaystyle {}_{}}$ P${\displaystyle m_{}}$ -${\displaystyle {}_{}{1}_{}}$ + ${\displaystyle {}_{}}$ ${\displaystyle m_{}}$]${\displaystyle a_{}}$m$$, { $displaystyle Y_{m$} [ 2 p_1 + $a_1$}로 $표시$됩니다.${\displaystyle }${\$displaystyle P_{m-1}=\sum$ _${i=1}^{m-1}a_{i$}}는$$ 지금까지 발견된 근사 제곱근입니다$.$이제 각각의 새로운 $추측$은 m$({$이 재귀성을 만족시켜야 한다는 것입니다.

$({displaystyle X_{m}=X_{m-1}-Y_{m})$

$초기화$ X ${\displaystyle {0\mathrm{}}_{}}$$$${\displaystyle {}_{}N}$. \ $displaystyle X$$_${ $0$} $=$ N . \ displaystyle X _ { m ${\displaystyle \}}$ \ $geq$n$$, \ $displaystyle$ 1 \ $leq$ m \ $leq$ n$$, .} ${\displaystyle X_{}}$ n$0$이면 $정확$한 $제곱근$을 찾을 수 있습니다$.$ 찾을 수 없는 경우$i$ {\$displaystyle a_{$} ${\displaystyle s_{}}$의 $합$은 제곱근의 적절한 근사치를 $나타내며{\displaystyle {}_{}}$ n {displaystyle$X_{$n$$}은 근사오차입니다.

예를 들어, 10진수 체계에서는

$\displaystyle N=(a_{1}\cdot 10^{n-1}+a_{2}\cdot 10^{n-2}+\cdots +a_{n-1}\cdot 10+a_{n}^{2}$

여기서 ${\displaystyle {10n}^{}}$ -$$i(\$displaystyle$ $10$$^{$$n-i})$는 자리 표시자이며 $계수{\displaystyle {}_{}}$ ${\displaystyle a_{}}$ {${\displaystyle 0}$ ,${\displaystyle 1}$, $2$,${\displaystyle }$…${\displaystyle }$, 9 $}$ $in$\ {$0 , 1$, 2, $\ldots$,$9$ 제곱근 계산의 임의의 m단계에서 지금까지 $발견$된 대략적인 루트${\displaystyle {,}_{}}$ $P$ - m - $style$1$aystyle$ Y_${m}}$은(는) 다음과 같습니다.

$\displaystyle P_{m-1}=\sum _{i=1}^{m-1}a_{i}\cdot 10^{n-i}=10^{n-m+1}\sum _{i=1}^{m-1}a_{i}\cdot 10^{m-1}$

$\displaystyle Y_{m}=[2P_{m-1}+a_{m}\cdot 10^{n-m}]a_{m}\cdot 10^{n-m}=\left[20\sum _ {i=1}^{i}a_{i}\cdot 10^{m-1}+a_{m_a}오른쪽]}$

${\displaystyle {여기}_{}}$서 Y m$(\$의 자리값은 10의 짝수이므로 m번째 스테이지에서는 ${\displaystyle X_{}}$m - $(\$X_${m-1$})의 나머지 $조건$의 최상위 자리 쌍만 사용하면 됩니다.다음 섹션에서는 이 절차를 코드화합니다.

십진수 체계 이외의 숫자 체계에서 제곱근을 계산할 때 유사한 방법을 사용할 수 있다는 것은 명백하다.예를 들어$,$ 이진수 시스템에서 자리수 제곱근을 찾는 것은 i\$style a_{i}$의 $값$이 더 작은 이진수 집합 {0,1}에서 검색되기 때문에 매우 효율적입니다.따라서 각 단계에서 Y$m의 값$은 Y ${\displaystyle m_{}}$ ${\displaystyle {}_{}}$$(m$$$${\displaystyle {}_{}}$ ${\displaystyle 0}$({${m$}$= 0)$ $또는$ ${\displaystyle Y_{}}$ m $=$ 2 ${\displaystyle P_{}}$ m - 1 + 1$(m)$이므로 $계산$이 $빨라집니다.$m$({$에 $사용$할 수 있는 옵션이 2개밖에 없기 때문에 m$({$의 $값$을 계산하는 과정도 쉬워집니다.${\displaystyle {이}_{}}$는 m ${\displaystyle {}_{}}$ 1.$${$displaystyle a_{m$} $=$ $1$에 대해$$ ${\displaystyle Y_{}}$ ${\displaystyle {}_{}}${\ ${\displaystyle \mathrm{X}}$ m -$$ {displaystyle Y_{$m$$}$ \$leq X_{m-1$$\}$의 여부만 확인하면 되기 때문입니다. 이 조건이 ${\displaystyle {충족}_{}}$되면 m${\displaystyle \mathrm{}}$$=$ 1 {$displaystyle a_{$m}$$${\displaystyle {}_{}}$ 1 ; {$displaystyle$ a_m= 1}이(${\displaystyle \mathrm{으}}$)이면 $.$e-by-left bit-param은 계산에 도움이 됩니다.

10진수(베이스 10)

원래 숫자를 십진법으로 쓰세요.숫자는 롱 나눗셈 알고리즘과 유사하게 쓰여지며 롱 나눗셈과 마찬가지로 루트는 위의 행에 쓰여집니다.자릿수를 소수점부터 시작하여 왼쪽과 오른쪽으로 두 개로 나눕니다.루트의 소수점은 제곱의 소수점보다 커집니다.제곱근의 한 자리는 정사각형의 각 자리 쌍 위에 표시됩니다.

왼쪽 끝의 자리수 쌍부터 시작하여 각 쌍에 대해 다음 절차를 수행합니다.

1. 왼쪽부터, 아직 사용되지 않은 가장 유의한(맨 왼쪽) 자리 쌍을 아래로 가져와서(모든 자리가 사용된 경우 "00"으로 적습니다), 이전 단계부터 나머지 오른쪽에 씁니다(첫 번째 단계에서는 나머지가 없습니다).즉, 나머지에 100을 곱하고 두 자릿수를 더하면 됩니다.이것이 현재 값 c가 됩니다.
2. 다음과 같이 p, y 및 x를 구합니다.
   • p는 지금까지 발견된 루트의 일부이며 소수점은 무시합니다.(첫 번째 단계의 경우 p = 0).
   • $x{\displaystyle }$ ${\displaystyle (}$ ${\displaystyle \mathrm{20}}$p +${\displaystyle x}$ )${\displaystyle c}$c \ $displaystyle$x ( $20p + x$ )\$leq$ c$$. 。새로운 변수 y = x ( 20p + x )를 사용합니다.
     • 주의: 20p + x는 단순히 2p이고 숫자 x는 오른쪽에 추가됩니다.
     • 주의: x는 c/(20·p)가 무엇인지 추측하고 y를 시험적으로 계산한 후 필요에 따라 x를 위아래로 조정하면 구할 수 있습니다.
   • $숫자{\displaystyle }$x(\$displaystyle$ x$)$를 루트의 다음 자리, 즉 방금 내린 정사각형의 두 자리 위에 배치합니다.따라서 다음 p는 오래된 p 곱하기 10 더하기 x가 됩니다.
3. c에서 y를 빼면 새로운 나머지가 된다.
4. 나머지가 제로이고, 다운할 디짓이 없어지면 알고리즘은 종료됩니다.그렇지 않으면 스텝1로 돌아가 다른 반복을 실시합니다.

예

152.2756의 제곱근을 구한다.

12.34/\/ 0152.27 56011*1<>=1<>2*2)=101는 y)x*x)1*1=1005222*2<>=52<>23*3)=20044는 y)(20+x)*x)22*2=440827243*3<>=827번지<>2.44*4)= 3 07 29 y = (240+x)*x = 243*3 = 729 98 56 2464*4 < = 9856 < 2465*5 x = 498 56 y = (2460+x)*x = 2464*4 = 9856 00 알고리즘 종료:답은 12.34입니다.

이진수 시스템(베이스 2)

이 섹션에서는 위의 숫자별 계산 섹션의 형식주의를 사용하며, $N{\displaystyle {}_{}}$ ${\displaystyle {2\mathrm{}}^{}}$ ${\displaystyle =}$ (${\displaystyle a_{}}$ +${\displaystyle {}_{}}$ +${\displaystyle {}_{}{}^{}{a\mathrm{}}_{}}$ 0 )$$ {{2} = ($a_{n} +\dotsb$ +$a_{0$2} = m =$$2$m$ {{$style a_{0$$}$ ${\displaystyle {}_{}}$ m } ${ or$ ${\displaystyle a_{}}$ a n n n n n n this this this this this n n n n this this n this this this n n n n n n n ${\displaystyle {\mathrm{}}^{}}$ n n n n $n{\displaystyle {}^{}}$
$(\$ 2$^{$$m$$\})$부터$$(\$displaystyle$ 2$^{n$까지 $모두{\displaystyle {\mathrm{}}^{}}$ $(\$$displaystyle$ 2^{m})를 반복하고, ${\displaystyle {근사해}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {}_{}}$ + ${\displaystyle {\mathrm{a}}_{}}$n -${\displaystyle }$1$$+$$ + $a _$ { { m$$} = a$_$ { n + a _ n + a + a + a _ ${\displaystyle {}_{}}$ + a + a + a + a + n + n + n + n + { n + n + { $1$} \ } \ } \ } + { n + { n + n + { n + { n + { n +가치를 정했습니다.
m$({$이 $({$ 2$^{m})$인지 $0{\displaystyle {}_{}}$$({$$display$ 0$\})$인지를 판별하기 ${\displaystyle {위해}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {}_{}}${$m}$ $= P_{m+1$} +$$^{$m$ 。${\displaystyle {If}_{}^{}}$ ${\displaystyle {\mathrm{}}_{}^{}}$ m 2 ${\displaystyle {n\mathrm{}}^{}}$N 2 ${\displaystyle {}_{}^{}}$ 2$$≤ N _$displaystyleq$$}$ } $2$ 。${\displaystyle {}^{}}$({$displaystyle$ 2$^{m})$ $그$ 후 m $=$ ${\displaystyle {2m}^{}}$({$displaystyle a_{m$}=$2^{m$ 이며, $그렇지{\displaystyle {}_{}}$ 않으면 ${\displaystyle m_{}}$ $=$$$${\displaystyle {}_{}}$ ({$displaystyle$ $a_{m$}=$0$$})$ 및$$ ${\displaystyle P_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {Pm}_{}}$ ${\displaystyle {+}_{}}$ ({$m+1$ 입니다$.$
각 단계에서 ${\displaystyle {Pm}_{}}$ ${$ $style$ $P_{m}$의 $제곱$을 피하기 위해 차이 ${\displaystyle X_{}}$ ${\displaystyle {}^{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {N\mathrm{}}^{}{2}_{}^{}}$ - ${\displaystyle {\mathrm{}}_{}^{}}$m 2 ({m} =$N ^$ ${$2} - $P _$ {$m}$$=$-$$ ($xisplay style X_{m$}) 를$$ $설정$하여 증분 갱신합니다.$displaystyle Y_{$$$$}^{2$
처음에는 (${\displaystyle {2\mathrm{}}^{}}$ n${\displaystyle {}^{}{}^{}}$ ${\displaystyle {\mathrm{}}^{}}$ ${\displaystyle {}^{}}$ ${\displaystyle 4^{}}$ n${\displaystyle {}^{}{n\mathrm{}}^{}}$N 2${\displaystyle {}^{}}$ N 2 { $display$style ($2^{n)^{2$} = 4$^{n}\leq$ N{$2}$인 $최대{\displaystyle }$ n$${$displaystyle$ n$}$에 대해 n ${\displaystyle {}_{}}$ $2$ ${\displaystyle n^{}}$ 2 n {displaystyle $a_{n$} =$$2 n} = 2 leq N^{$n$$\}$로 $설정$했습니다.

추가 최적화로 P${\displaystyle m_{}}$ + ${\displaystyle 1_{}}$ ${\displaystyle {}_{}{\mathrm{}}^m}$ + ${\displaystyle 1^{}}$ { $display$ $style$ P _ {$m$ +$1$}${\displaystyle }$$、$$$$（$ ${\displaystyle 2^{}}$ m$$） ${\displaystyle {2\mathrm{}}^{}}${ $display$ ( 2 ^ { $m$$)^$2$}$를 $저장$합니다.${\displaystyle {이것}_{}}$은$,$ ${\displaystyle Y_{}}$$m$의 2 개의 $항이{\displaystyle {}_{}}$, $별도$ $변수$입니다.${\displaystyle d_{m$

${\displaystyle c_{m}=P_{m+1}2^{m+1}}$

${\displaystyle d_{m}=(2^{m})^{2}}$

${\displaystyle Y_{m}=c_{m}+d_{m}}&{\text{if}}a_{m}=2^{m}\\0&{\text{if}}a_{m}=0\end{case}}$

${\displaystyle c_{}}$ m$${ $display$ style $c$_ { $m$} $d$ ${\displaystyle d_{}}$ d$$m { $display$ style $d$_ { $m$} c$$ 、 각 스텝에서 효율적으로 갱신할 수 있습니다.

${displaystyle c_{m-1}=P_{m}2^{m}=(P_{m+1}+a_{m}=P_{m+1}2^{m}=p_{begin{cases}ces_{m}+{m}+a_{m}2^{m}={text}}{text_a}} }$

${\displaystyle d_{m-1}=sublicfrac {d_{m}}{4}}$

주의:

${\displaystyle c_{}}$- ${\displaystyle 1_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {P\mathrm{}}_{}}$ 0 ${\displaystyle {2\mathrm{}}^{}}$ 0 $=$ ${\displaystyle {P\mathrm{}}_{}}$ 0 $=$ {\$displaystyle c_{-1$}= $P_{0}2^{0$}=$P_{0$}=$N$ 이는 아래 함수로 반환되는 최종 결과입니다.

C에서의 ^[5]이 알고리즘의 실장:

이진수 및 십진수 또는 기타 기준으로 더 빠른 알고리즘을 룩업 테이블을 사용하여 실현할 수 있습니다. 즉,^[6] 실행 시간을 단축하기 위해 더 많은 스토리지 공간을 교환할 수 있습니다.

지수 항등식

포켓 계산기는 일반적으로 지수함수와 자연대수를 계산하기 위한 좋은 루틴을 구현한 다음 로그(${\displaystyle {}^{}}$ x ${\displaystyle n^{}}$ ${\displaystyle {}^{}}$ ${\displaystyle n}$ ${\displaystyle }$ \ $displaystyle$ \$ln x$$=$ $n\$$ln$$$x$$)와 지수(${\displaystyle e^{}}$ ${\displaystyle {\ln }^{}}$ ${\displaystyle {}^{}}$ {\$display style$ e$^{\ln x}$ x)의 속성을 사용하여 찾은 항등식을 사용하여 S의 제곱근을 계산한다.$$):^{[citation needed]}

$({displaystyle {s}}=e^{\frac {1}{2}}\ln S})$

분수의 분모는 n번째 근에 해당합니다.위의 경우 분모는 2이므로 방정식은 제곱근을 구하도록 규정한다.로그 테이블 또는 슬라이드 규칙을 사용하여 제곱근을 계산할 때 동일한 ID가 사용됩니다.

이변수 반복 방법

이 방법은 0< < \ $displaystyle$0 <$3$ , \ ! $}$의 을 구하는데 적용할 수 있으며 S${\displaystyle 1}$ 1$$\ $displaystyle$S \ $about$1에$$$가장{\displaystyle }$ 적합합니다.단, 이것은 컴퓨터 기반 계산에는 실질적인 제한이 없습니다.이는 2차 부동소수점 표현과 고정소수점 표현에서는${\displaystyle }$S(\$displaystyle$ S$,\!)$에 4의 정수승, 즉 S$(\$에 2를 곱하는 것이 $간단하기{\displaystyle }$ 때문입니다.특히.$따라서$ $S$를${\displaystyle }$1 S < $s$ S $<$ 2$s$ S < 2 s 2 >로$이동할$수 있으며 다음 방법에서는 일반 나눗셈을 사용하지 않고 덧셈, 뺄셈, 곱셈 및 2의 곱셈만을 사용합니다.이 방법의 단점은 바빌로니아 방법과 같은 단일 변수 반복 방법과 대조적으로 수치 오류가 누적된다는 것이다.

이 메서드의 초기화 순서는 다음과 같습니다.

${\displaystyle a_{0}=S,\!}$

$(\displaystyle c_{0}=S-1,\!)$

반복 스텝이 판독되는 동안

${displaystyle a_{n+1}=a_{n}-a_{n}c_{n}/2,\!}$

${\displaystyle c_{n+1}=c_{n}^2}(c_{n}-3)/4,\!}$

${\displaystyle {그런}_{}}$ 다음 ${\displaystyle n\sqrt{}}$ $→$ S(\$style a_{n}\rightarrow {S})($${\displaystyle \mathrm{cn}}$ 0(\displaystyle $c_{n}\rightarrow$0}).$$

${\displaystyle c_{}}$${\displaystyle {}_{}}$n \ $display$ c$_$ { n$$} , \ ! $\}$ $c{\displaystyle {}_{}}$ therefore${\displaystyle {}_{}}$、 n \ $display style$ a _ { $n$} , \ !$$} 의 컨버전스는 2차입니다.

그 방법의 증명은 꽤 쉽다.먼저 $displaystyle c_{n},\!)$의 반복 정의를 다음과 같이 고쳐 씁니다.

${\displaystyle 1}$+ ${\displaystyle c_{}}$n + ${\displaystyle 1_{}}$ ${\displaystyle =}$ (${\displaystyle 1}$ + ${\displaystyle c_{}}$n${\displaystyle }$) (${\displaystyle 1}$ - ${\displaystyle c_{}}$n /${\displaystyle {}^{2\mathrm{}}}$ )$2$( \ $displaystyle$1 + $c$_ {$n$ + 1 } = ($1$ + $c _$ { $n$} / $2)^2$} ,$$\ !$$}

그렇다면 유도에 의해 증명하는 것은 간단하다.

${\displaystyle S(1+c_{n})=a_{n}^2}$

${\displaystyle {따라서}_{}}$ cn$(\$displaystyle $c_{n},\!)$을0으로 수렴함으로써 원하는 $결과{\displaystyle \sqrt{}}$ S(\$displaystyle {S})$에 대한 n${\displaystyle (\backslash {}_{}}$$displaystyle c_{n$의 수렴이 보장되며, 수렴은 -1 $0$에서0으로 $이어집니다$.

이 방법은 1950년경 M. V. Wilkes, D. J. Wheeler, S. Gill에^[7] 의해 최초의 전자 컴퓨터 ^[8]중 하나인 EDSAC에서 사용하기 위해 개발되었다.이 방법은 나중에 일반화되어 비제곱근 ^[9]계산을 가능하게 했다.

역제곱근에 대한 반복적 방법

다음은 S의 역제곱근인${\displaystyle }$1/$(\$ 1$/{\sqrt {S$를 구하는 반복 방법입니다. 찾은 후에는 단순 곱셈으로 S$(\$를 찾습니다.$S$ ${\displaystyle =}$ ${\displaystyle S}$ ${\displaystyle (}$ ( ${\displaystyle 1}$/${\displaystyle S\sqrt{}}$) { $displaystyle$ { s } $= S$ \ $cdot$($1$/ { \ $cdrt${ S$}$ )$$。이러한 반복에는 나눗셈이 아닌 곱셈만 포함됩니다.그러므로 그것들은 바빌로니아의 방법보다 빠르다.하지만, 그들은 안정적이지 않다.초기값이 역제곱근에 가깝지 않은 경우 반복은 수렴하기보다는 역제곱근에서 멀어집니다.따라서 이러한 방법을 적용하기 전에 대략적인 추정에서 바빌로니아 방법을 반복하는 것이 유리할 수 있다.

• ${\displaystyle \mathrm{식}}$ (1 / x${\displaystyle {}^{}{2\mathrm{}}^{}}$)${\displaystyle }$- ${\displaystyle S}$ $=$0 {$displaystyle (1/x^{2$} - S=$0$에$$뉴턴의$$ 방법을 적용하면 단계당 3배의 곱셈을 사용하여 2차적으로 수렴하는 방법이 생성됩니다.

  $({displaystyle x_{n+1}=cdot {x_{n}{2})\cdot(3-S\cdot x_{n}^2}=x_{n}\cdot \syslog\frac {3}{2}-{\frac {S}{n}^2}\오른쪽).}$

• 또 다른 반복은 Halley의 방법, 즉 세대주의 순서 2에 대한 방법에 의해 얻어진다.이것은 입방정식으로 수렴되지만 ^{[citation needed]}반복마다 5개의 곱셈이 필요합니다.

  ${\displaystyle y_{}}$ n $=$ ${\displaystyle S}$ ${\displaystyle †}$ ${\displaystyle {}_{}^{}}$ ${\displaystyle n_{}^{}}$ ({$displaystyle y_{n$}=$S\cdot x_{n}^{$2$\}\})$ 및

  $= displaystyle x_{n}}{8}}\cdot ( 15$$=x_{n}\cdot\frac${15$}{8}-y_{n}\cdot \leftfrac\frac {10}-{\frac$ {$3}{8$}\$cdot y_${n$}\$right$\}.$

• 고정 소수점 연산을 하는 경우, 시프트와 덧셈을 사용하여 3과 8의 곱셈을 구현할 수 있습니다.부동 소수점을 사용하는 경우, Halley의 방법은 ${\displaystyle \sqrt{\frac{\mathrm{3개}}{}}}$의 $(\displaystyle\sqrt\frac{3$}{8$}) S$를 사전 $계산$하고 다른 모든 상수를 보정하여 반복당 4배로 줄일 수 있습니다.

  ${\displaystyle y_{}}$ n ${\displaystyle {}_{}}$ ${\displaystyle 3\sqrt{\frac{\mathrm{}}{}}}$ ${\displaystyle \sqrt{\frac{8}{}}}$ ${\displaystyle \sqrt{S}}$ ${\displaystyle †}$ ${\displaystyle x_{}^{}}$ n$$ ({ $displaystyle y$_ { n } =$rt${ $frac${ $3$} { $8$} S \ $cdot x$_ { $n$}^2 $）$ 、

  ${\displaystyle {}_{}\frac{\mathrm{x}}{}{}_{}}$n + ${\displaystyle 1_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle n_{}{}_{}}$ ${\displaystyle \frac{8}{}}$ ${\displaystyle (}$ ${\displaystyle {}_{}}$ ${\displaystyle 8_{}}$ - y n${\displaystyle {}_{}}$ 25 ( ${\displaystyle \sqrt{\frac{25}{}}}$6 - ${\displaystyle y_{}}$n${\displaystyle }$)$${ $display$ x$_$ {$n$ + 1 } =$$x$$_ { n } \$cdot$\$left$ \ $frac${ $15$} { $8}$ - y $_ n$} \$cdot$\$left$\ $frac$ {$25$ } {$n$} \ $right$}

골드슈미트 알고리즘

일부 컴퓨터에서는 S$displaystyle\$$sqrt {S$$})$와 1/$S(\$displaystyle 1/{\sqrt {$S$를 $동시$에 계산하기 위해 Goldschmidt의 알고리즘을 사용합니다.Goldschmidt의 $알고리즘$은 퓨전된 파이프라인과 두 명령어 중 하나를 더한 컴퓨터에서 S$(\$sqrt ${S})$를 찾습니다.d 부동소수점 단위 또는 2개의 독립된 부동소수점 단위.^[10]

골드슈미트의 알고리즘을 쓰는 첫 번째 방법은

${\displaystyle b_{0}=S}$

${\displaystyle Y_{0}\approx 1/{\sqrt {S}}}$ (typically using a table lookup)

${\displaystyle y_{0}=Y_{0}}$

${\displaystyle x_{0}=Sy_{0}}$

반복하다

${\displaystyle b_{n+1}=b_{n}Y_{n}^{2}}$

${\displaystyle Y_{n+1}=(3-b_{n+1})/2}$

${\displaystyle x_{n+1}=x_{n}Y_{n+1}$

${\displaystyle y_{n+1}=y_{n}Y_{n+1}$

b$$\$displaystyle b_{i}$가 1에 충분히 가깝거나 일정한 반복 횟수에 도달할 $때$까지.반복은 로 수렴됩니다.

${\displaystyle \underset{}{lim}}$ n ${\displaystyle \underset{}{\to \mathrm{}}{}_{}}$ ${\displaystyle {nxn}_{}}$ $=$ {\$displaystyle \lim$ _${n\to \infty }x_{n$}=$sqrt {S$ 및

${\displaystyle \underset{}{lim}}$ n ${\displaystyle \underset{}{\to }}$ ${\displaystyle \underset{}{\mathrm{\infty }}}$ ${\displaystyle {ny}_{}}$ ${\displaystyle \mathrm{n}}$ $=$ ${\displaystyle 1\sqrt{}}$/ S { $displaystyle \lim$_ {$n\to$ \infty $}y_{n$}=$1/{\displayrt {S$

계산에서 ${\displaystyle x_{}}$n(\$displaystyle x_{n})$과 y $(\$}) 중 $하나$를 생략할 수 있으며, 둘 다 원하는 경우 x n $=$ ${\displaystyle S}$ ${\displaystyle y_{}}$n(\$displaystyle x_{n$}=$Sy_{n$})을 각 반복에서 계산하지 않고 ${\displaystyle {마지막}_{}}$에 사용할 수 있습니다.

퓨전된 다중 추가 연산을 사용하는 두 번째 폼이 시작됩니다.

${\displaystyle {y\mathrm{}}_{}}$ 0${\displaystyle {}_{}1}$1 /$$ { $display y$_ { 0$$} \ $about$ 1/ { \ $sqrt${$S$} $$（ using using using using) 。

${\displaystyle x_{0}=Sy_{0}}$

${\displaystyle h_{0}=y_{0}/2}$

반복하다

${\displaystyle r_{n}=0.5-x_{n}h_{n}}$

${\displaystyle x_{n+1}=x_{n}+x_{n}r_{n}}$

$\displaystyle h_{n+1}=h_{n}+h_{n}r_{n}$

$\$이(가) 0에 충분히 가깝거나 일정한 반복 횟수에 도달할 $때$까지.이것은 로 수렴됩니다.

${\displaystyle \underset{}{lim}}$ n ${\displaystyle \underset{}{\to \mathrm{}}{}_{}}$ ${\displaystyle {nxn}_{}}$ $=$ {\$displaystyle \lim$ _${n\to \infty }x_{n$}=$sqrt {S$ 및

${\displaystyle \underset{}{lim}}$ n ${\displaystyle \underset{}{\to }}$ ${\displaystyle \underset{}{\mathrm{\infty }}}$ ${\displaystyle \underset{}{}\mathrm{}}$ ${\displaystyle {hn}_{}}$ ${\displaystyle {}_{}1}$ /$$ ( \ $displaystyle$\ $lim$_${ n$ \$to$ \ infty }$2h$_ { n } =$1$/ { \ $syslogrt${ $S$} $\}$ }

테일러 급수

N이 S$(\$에 $대한{\displaystyle \sqrt{}}$ 근사치인 경우 제곱근 함수의 Taylor 시리즈를 사용하면 더 나은 근사치를 구할 수 있습니다.

${\displaystyle {N^{2}+d}}=N\sum _{n=0}^{\infty}{\frac {(-1)^{n}(2n)!}{(1-2n)n!^{2}4^{n}}{\frac {d^{n}}{N^{2n}}}=N\left(1+{\frac {d}{2})N^{2}}-{\frac {d^{2}}-{8N^{4}}+{\frac {d^{3}}{16N^{6}}-{\frac {5d^{4}}}-{128}N^{8}}+\cdots\right}$

반복 방법으로서 수렴 순서는 사용된 항의 수와 같습니다.두 개의 용어로, 그것은 바빌로니아 방식과 동일하다.세 개의 항을 사용하는 경우 각 반복은 Bakhshali 근사값과 거의 같은 수의 연산이 걸리지만 수렴 속도가 더 ^{[citation needed]}느립니다.따라서 이것은 특별히 효율적인 계산 방법은 아닙니다.컨버전스 속도를 최대화하려면 d ${\displaystyle \frac{N}{{}^{}}}$ $displaystyle\frac${ $d$}{$N^{2}},})$를 ${\displaystyle \frac{가능}{}}$한 작게 하도록 N을 선택합니다.

지속적 비율 확장

2차 비합리수${\displaystyle \frac{(a}{}}$ + b$$c { $displaystyle { frac${ a + { \$sqrt$ { b$}}$ {$c}}$ $형식$의 수$,$ 여기서 a, b 및 c는 정수) 및 특히 정수의 제곱근은 주기적인 연속 분수를 가진다.때때로 바람직한 것은 제곱근의 숫자 값이 아니라 연속적인 분수 팽창을 찾는 것이고, 따라서 합리적인 근사치를 찾는 것이다.S가 제곱근을 구하는 데 필요한 양수라고 하자.그런 다음 a가 초기 추측이 되고 r이 나머지 항이라고 가정하면, ${\displaystyle {}^{}}$ ${\displaystyle {}^{}}$ ${\displaystyle {a\mathrm{}}^{}}$ 2${\displaystyle }$+ ${\displaystyle r}$ 이라고 쓸 수 있다$$$.$ ({$displaystyle$ S ${\displaystyle =}$ $a ^$ ${$2$}$+ ${\displaystyle r}$ . }${\displaystyle }$S - ${\displaystyle a\sqrt{}}$(${\displaystyle S}$-${\displaystyle a\sqrt{}}$ ) $=$ ${\displaystyle r}$ ( \ $displaystyle$S - a$$^ { 2 } \ rt ( r ) { $rt }$ .

${\displaystyle {S}=a+{\frac {r}{a+{\displayrt {S}}}}$

분수의 분모 항에 S$(\$sqrt {$S})$에 대해 이 식을 적용하면 다음과 같이 됩니다.

${\displaystyle {S}=a+{\frac {r}{a+{\frac {r}}}}=a+{\frac {r}{2a+{\frac {r}{a+{\frac {r}}}}}}}.}$

이렇게 진행하면 제곱근에 대한 일반화 연속 분수가 S $=$ + ${\displaystyle \frac{r}{}}$ ${\displaystyle \frac{2}{}}$a + ${\displaystyle \frac{\frac{r}{}}{}}$ ${\displaystyle \frac{\frac{2}{}}{}}$a + ${\displaystyle \frac{\frac{\frac{r}{}}{}}{}}$ ${\displaystyle \frac{\frac{\frac{2}{}}{}}{}}$ a + r 2${\displaystyle \frac{\frac{\frac{}{}}{}}{}}$a + $⋱$ { $displaystyle${ displaystyle { $r$} {$2$ a + { \ $cfrac${$$r } { 2 a + { \ $cfrac${ $r }$ { 2 a + { \ $cfrac$ { r } + { 2$a$ + \ $ddots }}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$로 나옵니다.

루트를 얻기 위해 이러한 분수를 평가하는 첫 번째 단계는 원하는 숫자의 루트와 선택된 분모의 수에 대한 수치 치환을 수행하는 것입니다.예를 들어 표준 형식에서 $\displaystyle$r은$$ 1이고, for2의 $경우{\displaystyle }$\$displaystyle$a는$$ 1이므로 3개의 분모의 연속 분수는 다음과 같습니다.

${\displaystyle {\displaystyle {1}{2+{\displayac {1}{2+{\displayac {1}{2}}}}}$

2단계는 분자와 분모가 정수인 유리분수를 산출하기 위해 아래에서 위로 이어지는 분수를 한 번에 한 분모씩 줄이는 것입니다.감소는 다음과 같이 진행됩니다(처음 세 개의 분모를 사용).

${\displaystyle 1+{2+{\displayac {1}{2+{\displayac {1}{2}}}}=1+{\displayac {1}{\frac {5}}}}}$

${\displaystyle =1+{2+{\displayac {2}{5}}}=1+{\displayac {1}{\frac {12}{5}}}}$

${\displaystyle =1+{\displayac {5}{12}}=syslogfrac {17}{12}}$

마지막으로(3단계) 분자를 유리분수의 분모로 나누어 근의 근사값을 구한다.

${\displaystyle 1712}$ ${\displaystyle \mathrm{12\; =}}$ 1.${\displaystyle 42}$ {$displaystyle$ 17$\div$ 12$=1.$42$}$를 세 자리 정밀도로 반올림합니다.

2 의 실제치는 1.41 ~3 자리수의 유효치입니다.상대 오차는 0.17%이므로 유리 분율은 거의 세 자리 정밀도로 양호합니다.더 많은 분모를 취하면 연속적으로 더 나은 근사치를 얻을 수 있다. 4개의 분모는 분수 ${\displaystyle \frac{41}{}}$ 29 $=$}}=$1.4137$ 거의 4자리의 정밀도 등.

다음은 제곱근, 단순 연속 분수 및 분모 99까지의 첫 번째 항(컨버전트라고 함)의 예입니다.

§ S	~개요	연속 분수	컨버전스
22	1.41421	${\displaystyle [1;{\overline {2}}}$	${\displaystyle {\frac {3}{5}, {\frac {17}{12}, {\frac {41}{29}, {\frac {99}{70}}}$
33	1.73205	${\displaystyle [1;{\overline {1,2}}}}$	${\displaystyle {\frac {2}{1}, {\frac {5}{3}, {\frac {7}{4}, {\frac {19}{11}, {\frac {26}{15}, {\frac {714}, {\frac {97}{56)}$
5파운드	2.23607	$\displaystyle [2;{\overline {4}}}$	$\displaystyle {\frac {9} {4}, {\frac {38} {17}, {\frac {frac} {72)}$
66	2.44949	${\displaystyle [2;{\overline {2,4}}}}$	${\displaystyle {5}{2}, {\frac {22}{9}, {\frac {49){20}, {\frac {218}{89}}$
10파운드	3.16228	$\displaystyle [3;{\overline {6}}}$	${\displaystyle {19}{6}, {\frac {frac}{37}}$
$(\displaystyle {\pi }$	1.77245	${\displaystyle [1,3,2,1,1,6...]}$	${\displaystyle {\frac {2}{1}, {\frac {7}{4}, {\frac {16}{9}, {\frac {23}{13}, {\frac {39}{22}}}$
$(\displaystyle\displaystyle$	1.64872	${\displaystyle [1,1,1,5,1,1...]}$	${\displaystyle {\frac {2}, {\frac {3}, {\frac {28} {17}, {\frac {33) {20}, {\frac {611} {37}}$
$(\displaystyle(*displaystyle)$	1.27202	${\displaystyle [1;3,1,2,11,3,7...]}$	${\displaystyle {4}{3}, {\frac {5}{4}, {\frac {14}{11}}$

일반적으로 유리분수의 분모가 클수록 근사치가 높아집니다.또한 연속된 분수를 잘라내는 것은 분모가 분모의 분모보다 작거나 같은 분수의 근에 대한 최선의 근사인 합리적인 분수를 산출한다는 것을 보여줄 수 있다. 예를 들어, 분모가 70보다 작거나 같은 분모는 99/70보다 2에 대한 근사치만큼 좋은 분수는 없다.

루카스 배열법

제1종_n U(P,Q)의 루카스 시퀀스는 다음과 같은 반복 관계에 의해 정의된다.

${\displaystyle U_{n}(P,Q)="begin{case}0&{\text{if}}n=0\1&{\text{if}n=1\"P\cdot U_{n-1}(P,Q)-Q\cdot U_{n-2}(P,Q)&{\text{Otherwise}}\end{case}}$

그 특징적인 방정식은 다음과 같습니다.

${\displaystyle x^{2}-P\cdot x+Q=0}$

$판별{\displaystyle }$ ${\displaystyle {}^{}}$ ${\displaystyle {}^{}}$ P ${\displaystyle {2\mathrm{}}^{}}$ - ${\displaystyle 4}$Q({$displaystyle$ D$=P^{2}-4Q$})를$$ 가지며, 루트는 다음과 같습니다.

${\displaystyle {\sqrt {D}}{2},&x_{2}=sqrt {D}}{2}}{2}\end{matrix}}$

모두 다음과 같은 양의 값을 산출합니다.

$\displaystyle \lim _{n\to\infty}{\dfrac {U_{n+1}}{U_{n}}=x_{1}$

$따라서$ {{displaystyle ${a}}$을$($를) $원하는{\displaystyle \sqrt{}}$ 경우 P ${\displaystyle =}$ {{$displaystyle$ P$=2}$및$$ $Q{\displaystyle }$ ${\displaystyle {}_{}}$${\displaystyle 1}$${\displaystyle }$-$$a$${$displaystyle$ Q$=$$1-a}$를$$$선택$한 ${\displaystyle {다음}_{}}$ U${\displaystyle {}_{}}$+$$ {$displaystyle$ $x_{1$}=$1+{\displayrt {a$$}}$ $및{\displaystyle {}_{}}$ {n}을$($를) 사용하여 x1+${\displaystyle {1\mathrm{}}_{}}$)을 $계산$할 수 있습니다.${\displaystyle n}$ $\$ $display style$ n$$。${\displaystyle {Un}_{}}$+ $({$ $및$ $({$을 $계산$하는 가장 효과적인 방법은 다음과 같습니다.

$(\displaystyle \ bmatrix \U_{n}\U_{n+1}\end{bmatrix}=(begin{bmatrix}0&1\\-Q&P\end{bmatrix}\cdot {begin{bmatrix}U_{n-1}\\)U_{n}\end{bmatrix}=(begin{bmatrix}0&1\\-Q&P\end{bmatrix}^{n}\cdot{bmatrix})U_{0}\U_{1}\end{bmatrix}}$

요약:.

${\displaystyle {bmatrix} 0&1\a-1&2\end {bmatrix}^{n}\cdot {bmatrix} 0\\1\end {bmatrix}=cdot {bmatrix}U_{n}\U_{n+1}\end{bmatrix}}$

n ${\displaystyle \to }$→ { $displaystyle$n \ $to$\ $infty$ $\}$인 $경우{\displaystyle }$:

$({displaystyle {n+1}) {\displaystyle {\displayrt {a}} = flac {U_{n+1}}U_{n}}-1}$

부동소수점 표현에 따라 달라지는 근사치

숫자는 m${\displaystyle }$×$$(\$displaystyle$ m$\times$ b$^{p})$로 부동소수점 형식으로 표현되며 과학적 표기법이라고도 합니다.제곱근은 m${\displaystyle }$× ${\displaystyle b^{}}$p / $({$2$$})이며, 세제곱근과 로그에도 동일한 공식이 적용됩니다.외견상 단순성은 개선되지 않지만 ${\displaystyle {근사치}^{}}$만 요구된다고 가정하면 b p${\displaystyle {}^{}}$/ ${\displaystyle {2\mathrm{}}^{}}$(\$displaystyle$ b$^{p/2}})$ $정도$가 적당합니다.다음으로, 일부 거듭제곱 p는 홀수이므로 3141.59 = 3.14159×10일³ 때 기저의 분수제곱을 처리하는 대신 가수에 밑수를 곱하고 제곱에서 1을 빼서 균등하게 만든다.수정 표현은 31.4159×10과² 같게 되어 제곱근은 31.4159×10이¹ 된다.

조정된 가수의 정수 부분을 취하면 1부터 99까지의 값만 있을 수 있으며, 이 값은 미리 계산된 99개의 제곱근 테이블로 인덱스로 사용할 수 있어 추정을 완료할 수 있습니다.베이스 16을 사용하는 컴퓨터에서는 더 큰 테이블이 필요하지만 베이스 2를 사용하는 컴퓨터에서는 3개의 엔트리만 필요합니다.조정된 가수 정수 부분의 가능한 비트는 01입니다(정규화된 부동소수점 숫자는 항상 0이 아닌 상위 자리수를 갖는다는 것을 기억합니다).10개 또는 11개, 이것들은 원래 가수들의 첫 번째 두 조각입니다.따라서, 2진수에서는 6.25 = 110.01로 정규화되어 1.1001 × 2의² 짝수 전력으로 정규화되어 있고, 2진수에서는 .625 = 0.101로 정규화되어 있으므로 1.01⁻¹ × 2의 홀수 전력으로 조정은 10.1⁻² × 2로, 쌍수 비트는 10이다.전력의 하위 비트는 쌍방향 가수들의 상위 비트로 에코됩니다.짝수 전력은 하위 비트 0을 가지며 조정된 가수 값이 0으로 시작하는 반면 홀수 전력의 경우 해당 비트는 1이고 조정된 가수 값이 1로 시작됩니다.따라서 전력이 반감되면 하위 비트가 시프트되어 쌍방향의 첫 번째 비트가 되는 것과 같습니다.

엔트리가 3개뿐인 테이블은 가수 추가 비트를 포함시킴으로써 확장할 수 있습니다.그러나 컴퓨터에서는 표에 보간을 계산하는 것보다 더 간단한 계산을 통해 동등한 결과를 얻는 것이 더 낫습니다.이제 모든 것은 표현 형식의 정확한 세부 사항과 숫자의 일부에 액세스하고 조작하기 위해 사용할 수 있는 작업에 따라 달라집니다.예를 들어, Fortran이 제공하는 것은EXPONENT(x)동력을 얻기 위해 기능합니다.좋은 초기 근사치를 고안하는 데 들인 노력은 낮은 근사치에 필요했을 정제 프로세스의 추가적인 반복을 방지함으로써 회수해야 한다.이것들은 거의 없기 때문에(1회 반복에는 나눗셈, 덧셈 및 반분할이 필요) 제약이 심합니다.

많은 컴퓨터가 IEEE(또는 충분히 유사한) 표현을 따르며, 뉴턴의 방법을 시작하기 위해 제곱근에 대한 매우 빠른 근사치를 얻을 수 있습니다.다음 기법은 부동소수점 형식(기본값 2의)이 기본 2 대수에 가깝다는 사실에 기초하고 있습니다.${\displaystyle {이것}_{}}$은 ${\displaystyle {log}^{}}$ 2${\displaystyle \times }$ ( ${\displaystyle {}^{}}$× 2 ${\displaystyle p}$ )${\displaystyle =}$ ${\displaystyle p_{}}$ + ${\displaystyle {log\mathrm{}}_{}}$ 2${\displaystyle m}$( $m ){ displaystyle$ \$log$_ {2} $( m$ \ $times$ 2^ {p } =$$p + \ $log _$ {2} ( $m$) 。

따라서 IEEE 형식의 32비트 단정도 부동소수점 번호(특히 표시된 형식에 대해 127의 바이어스가 추가됨)의 경우 바이너리 표현을 32비트 정수로 해석하여$(\$ 2$^{-23$$만큼{\displaystyle {\mathrm{}}^{}}$ 스케일링하고 127의 바이어스를 제거함으로써 대략적인 로그를 얻을 수 있습니다.

${\displaystyle x_{\text{int}}\cdot 2^{-23}-display\log _{2}(x)입니다.}$

예를 들어 1.0은 16진수 숫자 0x3F800000으로 표시됩니다.정수로 하면 ${\displaystyle 1065353216}$ ${\displaystyle =}$ ${\displaystyle 127{\mathrm{}}^{}}$ ${\displaystyle 2^{}}$ 23 ${$ $displaystyle 1065353216= display\cdot$ 2$^{23}$을 나타냅니다.위의 수식을 ${\displaystyle {사용}_{}}$하면 로그 2${\displaystyle }$⁡ ( 1.$)\$ $displaystyle \log$ _ ${2}$ ($1.0$)에서 예상대로 ${\displaystyle 1065353216}$ - ${\displaystyle 23}$ - 127 ${\displaystyle =}$ { $displaystyle 1065353216$ \ $cdot$ 2 ^ { - $23$} - cdot =$0$} 이 됩니다.같은 방법으로 1.5 ( FC 3000 )로부터 0.5 를 얻을 수 있습니다.

제곱근을 구하려면 대수를 2로 나눈 다음 값을 다시 변환합니다.다음 프로그램은 아이디어를 보여줍니다.지수의 가장 낮은 비트는 의도적으로 가수에 전파될 수 있습니다.이 프로그램의 단계를 정당화하는 한 가지 방법은 b$(\displaystyle$ b$)$를 지수 $바이어스$라고 가정하고$n$(\$displaystyle$ n$)$을 가수에 명시적으로 저장된 비트 $수로{\displaystyle }$ 가정한 후 다음을 나타내는 것입니다.

$\displaystyle((x_{\text{int}/2^{n}-b)/b)\cdot 2^{n}=(x_{\text{int}-2^{n})/2+(b+1)/2)\cdot 2^{n}.}$

위의 함수의 핵심을 이루는 세 가지 수학적 연산은 한 줄로 표현될 수 있습니다.최대 상대 오차를 줄이기 위해 추가 조정을 추가할 수 있습니다.따라서 출연자를 제외한 세 가지 작업은

여기서 a는 근사 오차를 조정하기 위한 바이어스입니다.예를 들어 a = 0일 경우 2의 짝수 검정력(예: 1.0)에 대해서는 결과가 정확하지만, 다른 숫자에 대해서는 결과가 약간 너무 큽니다(예: 1.414가 아닌 2.0에 대해서는 1.5...).에러 6%).= -0x4B0D2의 경우 최대 상대 오차는 ±3.5%로 최소화됩니다.

Newton의 방법이 (${\displaystyle 1}$/ ${\displaystyle {x\mathrm{}}^{}}$2)${\displaystyle }$- ${\displaystyle S}$ ${\displaystyle =}$ {$displaystyle$ (1/$x^{2}-S=0$이라는 식으로 초기 추측할 때 근사치를 사용하는 경우, 다음 섹션에 표시된 역수 형식이 선호됩니다.

제곱근의 역수

위 루틴의 변형은 아래에 포함되어 있으며, 제곱근의 역수를 계산하는 데 사용할 수 있습니다. 즉${\displaystyle {,}^{}}$ x - ${\displaystyle {1\frac{\mathrm{}}{}}^{}}$ $({$ x$^{-{1 \over$ 2$)})$는 Greg Walsh에 의해 작성되었습니다.정수 편이 근사치는 4% 미만의 상대 오차를 발생시켰으며, 다음 ^[15]줄에 뉴턴 방법을 한 번 반복하면 오차는 0.15%로 더 떨어졌다.컴퓨터 그래픽스에서 그것은 벡터를 정규화하는 매우 효율적인 방법이다.

일부 VLSI 하드웨어는 Goldschmidt ^[16]반복에 이은 2차 다항식 추정을 사용하여 역제곱근을 구현합니다.

음수 또는 복소수 정사각형

S < 0인 경우, 그 주 제곱근은

${\displaystyle {S}=sqrt {\vert S\vert}},i,}$

만약 S = a+bi이고 여기서 a와 b는 실수이고 b는 0이면, 그 주 제곱근은 다음과 같다.

${\displaystyle {S}}=\frac S\vert +a}{2}},+,\operatorname {sgn}(b){\sqrt {\frac {\vert S\vert -a}{2}},i,}$

이는 ^[17][18]루트를 제곱하여 확인할 수 있습니다.여기서

$\displaystyle \vert S\vert = scsrt {a^{2}+b^{2}}}}$

S의 계수입니다.복소수의 주 제곱근은 음이 아닌 실수 부분을 갖는 근으로 정의됩니다.

「 」를 참조해 주세요.

• Alpha max + beta min 알고리즘
• n번째 루트 알고리즘
• 제곱근 2
• 정수 제곱근

메모들

레퍼런스

참고 문헌

외부 링크

• Weisstein, Eric W. "Square root algorithms". MathWorld.
• 뺄셈 제곱근
• 안드리야 라도비치의 정수 제곱근 알고리즘
• 퍼스널 계산기 알고리즘I : 제곱근 (윌리엄E)Egbert), Hewlett-Packard Journal(1977년 5월): 22페이지
• 제곱근을 학습하는 계산기