음지수 메타물질

Negative-index metamaterial
음지수 메타물질은 유리렌즈와 같은 일반적인 양지수 물질과 다르게 빛을 굴절 또는 굴절시킨다.

음지수 메타물질 또는 음지수 재료(NIM)는 전자파의 굴절률이 일부 주파수 범위에 [1]걸쳐 음의 값을 갖는 메타물질이다.

NIM은 단위 셀이라고 불리는 주기적인 기본 부품으로 구성되어 있으며, 일반적으로 외부에서 인가되는 전자 방사선의 파장보다 훨씬 작습니다.최초로 실험적으로 조사된 NIM의 단위 셀은 회로 기판 재료, 즉 와이어와 유전체로 구성되었습니다.일반적으로 이들 인위적으로 구축된 셀은 적층 또는 평면화되어 개별 NIM을 구성하기 위해 특정 반복 패턴으로 구성된다.예를 들어, 첫 번째 NIM의 단위 셀은 수평 및 수직으로 적층되어 반복 및 의도된 패턴이 생성되었습니다(아래 이미지 참조).

각 단위 셀의 응답 사양은 시공 전에 미리 결정되며, 새로 구성된 전체 재료의 의도된 응답에 기초한다.즉, 각 셀은 NIM의 바람직한 출력에 근거해 특정 방법으로 응답하도록 개별적으로 조정됩니다.총 응답은 주로 각 단위 셀의 기하학적 구조에 의해 결정되며 구성 물질의 응답과는 크게 다르다.즉, NIM이 반응하는 방법은 와이어나 금속, 유전체와는 달리 신소재입니다.따라서 NIM은 효과적인 미디어가 되었습니다.또한 이 메타물질은 사실상 "질서 있는 거시적 물질, 아래에서 위로 합성된 물질"이 되어 [2]그 성분을 넘어서는 새로운 성질을 가지고 있다.

굴절률에 음의 값을 나타내는 메타물질은 종종 몇 가지 용어 중 하나로 언급된다: 왼손잡이 매체 또는 왼손잡이 재료(LHM), 역파 매체(BW 매체), 음의 굴절률을 가진 매체, 이중 음(DNG) 메타물질 및 기타 유사한 이름.[3]

속성 및 특성

음의 굴절률을 생성하도록 배치된 분할링 공진기 어레이로, 구리 분할링 공진기와 파이버 유리 회로 기판의 연동 시트에 실장된 와이어로 구성됩니다.
전체 배열은 10×100×100mm 크기의 [4][5]3x20 단위 셀로 구성됩니다.높이 10밀리미터는 눈금자에 있는 6개의 분할 표시보다 조금 더 높게 측정되는데, 이는 인치 단위로 표시된다.

음의 굴절률을 가진 매체의 전기역학은 1967년 [6]모스크바 물리공과대학의 러시아의 이론물리학자 빅토르 베셀라고에 의해 처음 연구되었다.제안된 왼손잡이나 음의 색인 재료는 유리, 공기 및 다른 투명 매체의 것과 반대되는 광학 특성을 보이도록 이론화되었습니다.이러한 재료는 특이하고 예기치 않은 방식으로 휘어지거나 굴절되는 빛과 같은 직관적인 특성을 보일 것으로 예측되었다.그러나 최초의 실용적인 메타물질은 33년이 지나서야 만들어졌고 베셀라고의 [1][3][6][7]개념을 만들어냈다.

현재 음의 지표 메타물질은 전자파를 새로운 방식으로 조작하기 위해 개발되고 있다.예를 들어, 자연 물질의 광학 및 전자기적 특성은 종종 화학을 통해 변화한다.메타물질로 단위세포의 기하학적 구조를 변경함으로써 광학 및 전자파 특성을 엔지니어링할 수 있습니다.단위 셀은 방사된 전자파의 파장의 일부인 치수를 갖는 기하학적 배열로 정렬된 물질입니다.각 인공 유닛은 소스로부터의 방사선에 반응합니다.종합 결과는 [1][3][7]정상보다 넓은 전자파에 대한 물질의 반응이다.

그 후 단위 셀의 형상, 크기 및 구성을 조정하여 전송을 변경한다.이를 통해 유전율 및 자기 투과성으로 알려진 재료 매개변수를 제어할 수 있습니다.이 두 가지 파라미터(또는 수량)에 의해 물질 내 전자파의 전파가 결정됩니다.따라서 유전율 및 투과율 값을 제어한다는 것은 굴절률이 음수 또는 0이 될 수 있고 기존의 양수일 수 있다는 것을 의미한다.이 모든 것은 의도한 응용 프로그램 또는 원하는 결과에 따라 달라집니다.따라서 광학 특성은 렌즈, 거울 및 기타 기존 재료의 능력 이상으로 확장될 수 있습니다.또한 가장 많이 연구된 효과 중 하나는 음의 [1][3][6][7]굴절률이다.

역전파

음의 굴절률이 발생하면 전자파의 전파가 역전된다.회절 한계 이하의 분해능이 가능해진다.이를 서브파장 이미징이라고 합니다.전자적으로 평평한 표면을 통해 광선을 전달하는 것도 또 다른 기능입니다.반면 기존 재료는 보통 곡선으로 되어 있어 회절 한계 이하의 분해능을 얻을 수 없다.또한 재료의 전자파를 다른 일반 재료(공기 포함)와 함께 반전시키면 일반적으로 [1][3][6][7]발생하는 손실을 최소화할 수 있다.

반평행 위상 속도로 특징지어지는 전자파의 역방향도 음의 [1][6]굴절률의 지표이다.

또한 음지수 재료는 맞춤형 복합재료이다.즉, 재료는 원하는 결과를 염두에 두고 조합됩니다.소재의 조합은 자연에서는 볼 수 없는 광학적 특성을 실현하도록 설계할 수 있습니다.복합 재료의 특성은 충돌 전자파장보다 작은 구성요소로 구성된 격자 구조에서 비롯되며 충돌 전자파장보다 작은 거리로 구분됩니다.이와 같이, 그러한 메타 물질을 제작함으로써, 연구원들은 빛의 [1][3][7]파장과 관련된 근본적인 한계를 극복하려고 노력하고 있다.비일상적이고 직관적인 특성은 현재 무선 및 통신 시스템에서 전자파를 조작하는 실용적이고 상업적인 용도로 사용되고 있습니다.마지막으로 가시광선을 [7][8]포함한 전자기 스펙트럼의 다른 영역에서 연구가 계속된다.

자재

최초의 실제 메타물질은 전자파 스펙트럼(약 4.3GHz)의 마이크로파(cm 파장)에서 작동했다.스플릿 링 공진기와 직선(단위 셀)으로 구성되었습니다.단위 셀의 크기는 7mm에서 10mm 사이였습니다.단위 셀은 2차원(주기적) 반복 패턴으로 배열되어 결정과 같은 형상을 생성합니다.단위 셀과 격자 간격 모두 방사 전자파보다 작았다.이것은 물질의 유전율과 투과율이 모두 음수였을 때 최초의 왼손잡이 물질을 생산했다.이 시스템은 단위 셀의 공명 동작에 의존합니다.아래에 있는 연구자 그룹은 그러한 공명 행동에 의존하지 않는 왼손잡이 메타물질에 대한 아이디어를 개발한다.

마이크로파 범위에서의 연구는 분할 링 공진기와 전선 도체로 계속됩니다.또한 이러한 재료 구성으로 더 짧은 파장에서 연구를 계속하고 단위 셀 크기를 축소합니다.단, 약 200 테라헤르츠에서는 분할 링 공진기를 사용하는 데 문제가 발생합니다."대체 재료가 테라헤르츠 및 광학 체제에 더 적합하게 되었습니다."이러한 파장에서는 재료의 선택과 크기 제한이 중요합니다.[1][4][9][10]예를 들어 2007년에는 은으로 만든 100나노미터 메시 와이어 설계가 가시 스펙트럼의 끝인 780나노미터 파장에서 빔을 전송했습니다.연구원들은 이것이 0.6의 음의 굴절을 발생시켰다고 믿는다.그럼에도 불구하고, 이것은 마이크로파 시스템의 이전 메타 물질과 같은 단일 파장에서만 작동한다.따라서 메타물질을 제작하여 "더 작은 파장에서 빛을 반사"하고 광대역 [11][12]능력을 개발하는 것이 과제입니다.

인공 송전선 매체

주요 기사:메타물질 안테나
Artificial transmission-line-media.png

메타물질 문헌에서 매체 또는 매체란 전송매체 또는 광학매체를 말한다.2002년, 공진 거동에 의존하는 재료와 달리, 비공진 현상은 와이어/분할링 공진기 구성의 좁은 대역폭 제약을 초과할 수 있다는 연구자 그룹이 아이디어를 내놓았다.이 아이디어는 넓은 대역폭 능력, 음의 굴절, 역방향 파동 및 회절 한계를 넘는 초점을 가진 매체로 변환되었습니다.

스플릿 링 공진기를 사용하지 않고 대신 L–C 부하 전송로 네트워크를 사용했습니다.메타물질 문헌에서 이것은 인공 전송 선로 매체로 알려지게 되었다.그 당시에는 와이어와 분할 링 공진기로 만들어진 유닛보다 더 콤팩트하다는 추가적인 장점이 있었습니다.네트워크는 확장 가능하고(메가헤르츠에서 수십 기가헤르츠까지) 조정 가능합니다.또한 관심 [13]파장의 초점을 맞추는 방법도 포함한다.2007년까지 부굴절률 전송선은 자유공간 평탄렌즈에 초점을 맞춘 부파장으로 사용되었다.이것이 자유 공간 렌즈라는 것은 상당한 발전이다.이전 연구 작업의 일부는 [14]전송로에 삽입할 필요가 없는 렌즈를 만드는 것을 목표로 했습니다.

광학 도메인

주요 기사:포토닉 메타물질 및 플라스몬 메타물질

메타물질 성분은 적외선 및 가시 스펙트럼에서 전자기 스펙트럼의 짧은 파장(높은 주파수)을 탐색함에 따라 축소된다.예를 들어 이론과 실험에서는 석판화 [15][16]기술로 설계된 말발굽 모양의 분할링 공진기, 금속 나노로드 또는 나노스트립 [17]쌍, 나노입자를 일괄 소자 모델로 설계된 회로로 조사했다.

적용들

음지수 재료의 과학은 케이블, 전선 또는 공기를 통해 이동하는 전자파 신호를 방송, 송신, 형상화 또는 수신하는 기존 장치와 일치하고 있습니다.이 작업과 관련된 재료, 장치 및 시스템은 특성이 변경되거나 강화될 수 있습니다.따라서, 이것은 이미 상업적으로 이용 가능한[19] 메타물질 안테나 및 관련 장치에서 일어나고 있습니다.더욱이, 무선 영역에서 이러한 메타물질 장치들은 계속 연구되고 있습니다.다른 응용 프로그램도 조사 중입니다.여기에는 레이더 마이크로웨이브 흡수기, 전기적으로 작은 공진기, 회절 한계를 초과할 수 있는 도파관, 위상 보상기, 초점 장치(예: 마이크로파 렌즈)의 진보, 개선된 전기적으로 작은 [20][21][22][23]안테나 등의 전자파 흡수기가 있습니다.

광주파수 영역에서 슈퍼렌즈를 현상하면 회절 한계 미만의 이미징을 허용할 수 있다.음지수 메타 재료의 다른 잠재적 응용 분야로는 광학 나노 리소그래피, 나노 기술 회로 및 생물의학 이미징 및 준파장 사진 [23]리소그래피에 유용할 수 있는 근거리 초광대(Pendry, 2000)가 있다.

유전율 및 투과율 조작

굴절률이 다른 두 매체의 계면에서의 빛의 굴절은 n > n이다21.두 번째 매질(v21 < v)에서는 속도가 낮기 때문에 굴절각 θ는2 입사각 θ보다1 작으며, 즉 고지수 매질 내의 광선은 정점에 가깝다.

광학렌즈와 같은 특정 아퀴랄 소재의 전자기적 특성을 설명하기 위해 두 가지 중요한 매개변수가 있습니다.유전율, r\ \ _ { 투과율 r \ \_ { 등 물질 내를 이동하는 광파를 정확하게 예측할 수 있는 것, 두 [24]물질 간 계면에서 발생하는 전자파 현상 등이다.

예를 들어 굴절은 두 물질 사이의 계면에서 발생하는 전자기 현상입니다.Snell의 법칙에 따르면 전자파(빛) 빔의 입사각과 그에 따른 굴절각 사이의 관계는 두 매체(물질)의 굴절률 에 달려 있습니다.아퀴랄 매질의 굴절률은 n ± r \n=\n[25]으로 나타내며, 따라서 굴절률은 이 두 가지 파라미터에 따라 달라지는 것으로 볼 수 있다.따라서 r \ \_ { 및 r \ \_ {의 값을 설계 또는 임의로 변경할 수 있으면 재료 내부의 전자파 전파 거동을 마음대로 조작할 수 있다.그런 다음 이 능력을 [24]통해 굴절률을 의도적으로 결정할 수 있습니다.

균일한 평면 인터페이스에서의 빛의 마이너스 굴절을 나타내는 비디오.

예를 들어 1967년에 Victor Veselago는 음의 굴절률을 가진 물질과 종래의 양의 굴절률을 나타내는 물질 사이의 계면에서 빛이 역방향(음)으로 굴절한다고 해석적으로 결정했다.이 특별한 소재는 r {\ _ 및 r {\ \ _r에 대해 동시에 음의 값을 갖는 종이에서 실현되었으므로 이중 음의 소재라고 할 수 있다.그러나 베셀라고 시대에는 이러한 효과를 낼 수 있는 천연물질이 존재하지 않기 때문에 이중의 음의 매개변수를 동시에 나타내는 물질은 불가능해 보였다.그러므로,[24] 그의 작품은 30년 동안 무시되었다.그것은 나중에 노벨상 후보에 올랐다.

일반적으로 천연 물질의 물리적 특성은 한계를 일으킨다.대부분의 유전체에는 양의 유전율 r \ _ { >0 만이 있습니다.금속은 광주파수에서음의 유전율을 는 특정 주파수 대역에서 음의 유전율 값을 Pendry 등은 벌크 금속을 대체하는 금속 막대로 만들어진 재료를 사용하여 금속의 경우 낮은 마이크로파 주파수에서 플라즈마 주파수를 발생시킬 수 있음을 입증했다.그러나 이러한 경우 각각 투과성은 항상 양성으로 유지됩니다.마이크로파 주파수에서는 일부 강자성 물질에서 음의 μ가 발생할 수 있습니다.그러나 본질적인 단점은 테라헤르츠 이상의 주파수를 찾기 어렵다는 것입니다.어느 경우든 유전율과 투과율을 동시에 음의 값을 얻을 수 있는 천연물질은 발견되지 않았다.따라서, 이 모든 것이 [24]원하는 결과를 얻기 위해 메타물질로 알려진 인공 복합 재료를 만드는 것으로 이어졌다.

키라리티에 의한 음의 굴절률

키랄 소재의 경우 n {\n}은 r {\\} 및 \r에 따라 좌우 원형 폴라 값이 구별된다.레이즈드 웨이브, 에 의해 주어지는

만약 κ{\displaystyle \kappa}을 부정적인 지수 한 원형 편광의 파도를, 발생할 것이다 ϵ rμ r(_{r}}}}. 이 경우, 그것은 필요하지 않은 또는 둘 다ϵ r{\displaystyle \epsilon_{r}}과μ r{\displaystyle \mu_{r}}부정적인에 achi.이브음의 굴절률키랄리티로 인한 음의 굴절률은 펜드리와 트레티아코프 [27]등이 예측했으며[26] 2009년 플럼과 [28]장 [29]등이 동시에 독립적으로 처음 관찰했다.

자연에서 생산된 적이 없는 물리적 특성

1996년과 1999년에 이론적인 논문이 발표되었는데, 이는 합성 재료가 의도적으로 음의 유전율과 [note 1]투과성을 나타내도록 구성될 수 있다는 것을 보여주었다.

이 논문들은 1967년 베셀라고의 음지수 물질의 성질에 대한 이론적 분석과 함께 음의 유효 유전율과 [30][31][32]투과성을 가진 메타 물질을 만드는 배경을 제공했다.이하를 참조해 주세요.

음의 지수 거동을 나타내기 위해 개발된 메타물질은 일반적으로 개별 성분에서 형성된다.각 구성요소는 물질을 통과할 때 방사된 전자파에 대해 서로 다르게 독립적으로 반응합니다.이러한 구성요소는 복사 파장보다 작기 때문에 거시적 시야에는 유전율과 [30]투과율 모두에 대한 유효값이 포함되어 있는 것으로 이해된다.

복합 재료

2000년에 데이비드 R. Smith의 UCSD 연구팀은 일련의 얇은 구리 분할 링과 링에 평행하게 늘어선 일반 와이어 세그먼트로 구성된 회로 기판 위에 구조를 퇴적시킴으로써 새로운 종류의 복합 재료를 생산했습니다.이 물질은 자연에서 관찰된 적이 없는 특이한 물리적 특성을 보였다.이들 물질은 물리 법칙을 따르지만 일반 물질과는 다르게 작용합니다.본질적으로 이러한 음의 지수 메타물질은 일반적인 광학물질의 동작을 지배하는 많은 물리적 특성을 반전시킬 수 있는 능력을 가진 것으로 알려져 있다.그 특이한 특성 중 하나는 스넬의 굴절 법칙을 처음으로 뒤집는 능력이다.UCSD 팀이 마이크로파에 대한 음의 굴절률을 입증하기 전까지는 이 물질을 사용할 수 없었습니다.1990년대 제작 및 계산 능력의 발전으로 이러한 최초의 메타물질은 제작될 수 있었다.따라서, "새로운" 메타물질은 30년 전에 Victor Veselago에 의해 묘사된 효과에 대해 테스트되었다.그 직후에 이어진 이 실험에 대한 연구는 다른 효과가 [5][30][31][33]발생했다고 발표했다.

반강자석 및 특정 유형의 절연 강자석을 사용하면 폴라리톤 공명이 존재할 때 효과적인 음의 자기 투과율을 달성할 수 있습니다.단, 음의 굴절률을 달성하려면 음의 값을 갖는 유전율이 동일한 주파수 범위 내에서 발생해야 합니다.인공적으로 제작된 스플릿링 공진기는 높은 손실의 감쇠와 더불어 이를 실현하는 설계입니다.메타물질의 첫 도입으로 발생한 손실은 반강자성, 즉 강자성 [5]물질보다 작았던 것으로 보인다.

2000년에 처음 시연되었을 때 복합 물질(NIM)은 4-7기가헤르츠(4.28-7.49cm 파장)의 주파수에서 마이크로파 방사선을 전송하는 것으로 제한되었다.이 범위는 가정용 전자레인지 주파수(~2.45GHz, 12.23cm)와 군사용 레이더(~10GHz, 3cm) 사이입니다.실증된 주파수에서 재료를 [5][33][34]한 방향으로 이동하는 전자방사의 펄스는 반대 방향으로 이동하는 구성파로 구성된다.

메타물질은 회로기판 기판에 퇴적된 구리 분할 링과 와이어 전도 소자의 주기적 배열로 구성되었습니다.이 설계는 셀과 셀 사이의 격자 간격이 방사된 전자파장보다 훨씬 작도록 했습니다.따라서 효과적인 매체 역할을 합니다.이 물질은 (유효한) 유전율 δeff 및 투과율eff μ 값의 범위가 일반 물질에서 발견되는 값을 초과했기 때문에 주목받게 되었다.또, 일반 재료에서는 볼 수 없었던 음(유효한) 투과성의 특성이 특히 두드러진다.또한 자기 성분에 대한 음의 값은 왼쪽 명명법 및 특성과 직접 관련이 있습니다(아래 절에서 설명).Split-Ring Resonator(SRR; 분할링 공진기)는 1999년 이전의 이론 논문에 기초하고 있으며, 음의 투과율을 달성하기 위해 사용되는 도구입니다.이 첫 번째 복합 메타물질은 분할 링 공진기와 전기 전도 [5]포스트로 구성됩니다.

처음에 이 물질들은 가시 스펙트럼의 물질보다 긴 파장에서만 입증되었다.또한 초기 NIM은 불투명한 재료로 제작되었으며 일반적으로 비자성 성분으로 제작되었습니다.다만, 예를 들면, 이러한 재료가 가시 주파수로 구성되고, 그 결과 발생하는 NIM 슬래브에 손전등을 비추는 경우, 재료는 반대쪽의 한 점에 빛을 집중시켜야 합니다.일반 불투명 [1][5][33]재료 시트로는 불가능합니다.2007년 NIST는 Caltech의 Atwater Lab과 협력하여 광 주파수로 활성화된 최초의 NIM을 만들었습니다.최근에는 (2008년 현재) 실리콘 및 은선으로 이루어진 레이어드 "피시넷" NIM 재료가 광섬유에 통합되어 활성 광학 소자를 [35][36][37]만들고 있습니다.

음전율 및 투과율 동시

음의 유전율 δeff < 0은 최초의 메타물질 이전에 이미 금속에서 플라즈마 주파수까지의 주파수로 발견되어 실현되었다.굴절의 음의 값을 얻기 위한 두 가지 요건이 있습니다.첫째, 음의 투과율eff μ < 0을 생성할 수 있는 재료를 제작하는 것이다. 둘째, 공통 [1][30]주파수 범위에서 유전율과 투과율 모두에 대한 음의 값이 동시에 발생해야 한다.

따라서 첫 번째 메타물질의 경우 너트와 볼트는 하나의 (전기) 전도 포스트와 전자적으로 결합된 하나의 분할링 공진기이다.이들은 지정된 주파수로 공진하여 원하는 값을 달성하도록 설계되어 있습니다.스플릿 링의 구성을 보면 SRR로부터의 관련 자기장 패턴이 쌍극자입니다.이것은 자연의 원자를 모방한다는 것을 의미하기 때문에 이 쌍극자의 행동은 주목할 만하지만, 이 경우에는 2.5mm로 훨씬 더 큰 규모로 나타납니다.원자는 피코미터 단위로 존재한다.

링의 분할에 의해 SRR 유닛 셀이 링 직경보다 훨씬 큰 방사 파장에서 공명할 수 있는 다이내믹이 생성됩니다.고리가 닫히면 반파장 경계가 [5]공명의 요건으로 전자기적으로 부과된다.

두 번째 링의 스플릿은 첫 번째 링의 스플릿과 반대 방향입니다.작은 갭에서 발생하는 큰 캐패시턴스를 생성하기 위해서입니다.이 캐패시턴스는 전기장에 집중하면서 공진 주파수를 크게 낮춥니다.오른쪽에 표시된 개별 SRR의 공진 주파수는 4.845GHz이며, 그래프에 삽입된 공진 곡선도 표시되어 있습니다.단위 치수가 자유 공간인 복사 [5]파장보다 훨씬 작기 때문에 흡수 및 반사에 의한 복사 손실은 작은 것으로 알려져 있다.

이들 유닛 또는 셀이 주기적인 배열로 결합되면 공진기 간의 자기 결합이 강화되고 강한 자기 결합이 발생합니다.일반 재료나 기존 재료에 비해 독특한 특성이 나타나기 시작한다.우선, 이 주기적인 강한 결합은 물질을 생성하며, 이제 방사-입사 [5]자기장에 반응하는 효과적인 자기 투과율eff μ를 갖게 된다.

복합 재료 통과 밴드

일반 분산 곡선을 그래프로 나타내면 전파 영역은 0에서 낮은 밴드 가장자리까지, 그 다음에 갭, 그리고 위쪽 통과 밴드가 차례로 발생합니다.4.2GHz와 4.6GHz 사이에 400MHz의 갭이 존재하는 것은 μ < 0이 발생하는 주파수eff 대역을 의미합니다.

(이전 섹션의 이미지를 참조하십시오.)

또, 분할 링간에 대칭적으로 와이어가 추가되면, 분할 링 분산 곡선의 미리 금지되어 있던 대역내에서 패스 밴드가 발생한다.이전에 금지되었던 영역 내에서 이 패스밴드가 발생한다는 것은 이 영역의 음의 μ가eff 음의eff μ와 결합되어 전파가 가능함을 나타냅니다.이것은 이론적인 예측에 들어맞습니다.수학적으로 분산관계는 모든 곳에서 음의 군속도를 갖는 대역과 플라즈마 주파수에 의존하지 않는 대역폭으로 [5]이어진다.

수학적 모델링과 실험 모두 주기적으로 배열된 전도 소자(본성적으로 비자성)가 주로 입사 전자장의 자기 성분에 반응한다는 것을 보여주었다.그 결과 주파수 대역에 걸쳐 유효한 매질과 음의eff μ가 됩니다.투과성은 제한된 재료 구간에서 전파 갭이 발생한 금지 대역의 영역인 것으로 검증되었다.이것은 음의 유전율 물질인 δeff < 0과 결합되어 "왼손잡이" 매질을 형성했다. 매질은 이전에는 감쇠만 있었던 곳에서 음의 그룹 속도를 가진 전파 대역을 형성했다.이 검증된 예측입니다.또한, 이후 연구에서는 이 첫 번째 메타물질은 굴절률이 하나의 전파 방향에 대해 음이 될 것으로 예측되는 주파수 범위를 가지고 있다는 것을 알아냈다(참조 [1]번호 참조).다른 예측된 전기역학적 효과는 다른 연구에서 [5]조사하기로 했다.

왼손잡이 재료 설명

음지수 메타물질과 동일하지만 양의 굴절률을 가진 기존 재료의 굴절률 비교.입사빔 θ는 공기에서 입사하여 정상(θ') 또는 메타물질(-θ')로 굴절된다.

위 섹션의 결론에서 왼손잡이 재료(LHM)를 정의할 수 있습니다.중복 주파수 영역에서 유전율 δ와 투과율 μ에 대해 동시에 음의 값을 나타내는 물질이다.이 값은 복합매체계 전체의 영향에서 도출되므로 유효유전율, δeffeff 및 유효투과율 μ로 정의되며, 다음으로 음의 굴절률 및 파동 벡터의 값을 나타내는 실수값이 도출된다.이는 실제로 마이크로파, 적외선 주파수, 가시광선 등의 전자파 복사에 사용되는 특정 매체에 대해 손실이 발생한다는 것을 의미한다.이 경우, 실제 값은 무시할 수 있는 손실 값을 [4][5]무시한 채 입사파에 대한 송신파의 진폭 또는 강도를 나타냅니다.

2차원의 등방성 음수 지수

위 절에서 첫 번째 가공 메타물질은 공명 요소로 구성되었으며, 이는 입사 및 편광의 한 방향을 나타낸다.즉, 이 구조물은 일차원적으로 왼손 전파를 보였다.이것은 33년 전 베셀라고의 중요한 작업과 관련하여 논의되었다.그는 유효 유전율과 투과성의 음의 값을 나타내는 물질에 내재하는 여러 종류의 역물리학 현상이라고 예측했다.따라서, 예상대로 베셀라고의 이론을 확인할 고차원 LHM이 매우 중요했습니다.확인에는 스넬의 법칙(굴절률 지수)의 반전이 포함되며 다른 반전 현상도 포함된다.

2001년 초에 고차원 구조의 존재가 보고되었다.그것은 2차원적이었고 실험과 수치적 확인을 통해 입증되었다.LHM은 분할링 공진기(SRR) 뒤에 정기적인 구성으로 장착된 와이어 스트립으로 구성된 복합체입니다.Veselago가 [4]예측한 효과를 내기 위한 추가 실험에 적합하다는 명확한 목적을 위해 만들어졌습니다.

음의 굴절률 실험 검증

한쪽이 분할된 내부 정사각형으로 이루어진 분할링 공진기. 바깥쪽 정사각형에 다른 한쪽이 분할된 경우.스플릿 링 공진기는 사각 그리드의 전면과 우측 표면에 있으며, 단일 수직 와이어는 후면과 좌측 [5]표면에 있습니다.

1967년 소련의 물리학자 빅토르 베셀라고가 발표한 이론 연구는 음의 값을 갖는 굴절률이 가능하고 이것이 물리 법칙에 위배되지 않는다는 것을 보여주었다.앞서 (위에서) 논의한 바와 같이, 첫 번째 메타물질은 굴절률이 하나의 전파 방향에 대해 음이 될 것으로 예측되는 주파수 범위를 가지고 있었다.그것은 2000년 [1][6][38]5월에 보고되었다.

2001년 연구팀은 음의 굴절률을 실험적으로 테스트하기 위해 메타물질(음성지수 메타물질)로 구성된 프리즘을 만들었다.실험은 도파관을 사용하여 적절한 주파수를 전송하고 물질을 분리했습니다.이 테스트는 음의 [1][6][39][40][41][42][43]굴절률을 성공적으로 검증했기 때문에 목적을 달성했다.

음의 굴절률에 대한 실험적인 증명은 2003년에 스넬의 법칙의 반전, 즉 역굴절의 또 다른 증명에 이어 이루어졌다.그러나 이 실험에서는 굴절물질의 음지수가 12.6GHz에서 13.2GHz 사이의 빈 공간에 있다.방사 주파수 범위는 거의 동일하지만 눈에 띄는 차이점은 이 실험이 [44]도파로를 사용하는 대신 빈 공간에서 수행된다는 것입니다.

또, 부굴절의 진위를 산출해, 분산 왼손 재료를 투과하는 파의 파워 플로우를 산출해, 분산 오른손 재료와 비교했다.등방성 비분산 물질에서 등방성 분산 매체로 다수의 주파수로 구성된 입사장의 전송이 사용된다.비분산 매체와 분산 매체의 전력 흐름 방향은 시간 평균 포인팅 벡터에 의해 결정됩니다.LHM의 [45]포인팅 벡터를 명시적으로 계산함으로써 다중 주파수 신호에 대해 음의 굴절이 가능한 것으로 나타났습니다.

NIM의 기본 전자 특성

일반적인 굴절률(RHM)을 가진 재래식 재료의 슬래브에서는 파면(front)이 소스로부터 멀리 전송됩니다.NIM 에서는, 웨이브 프런트(wavefront)가 송신원을 향해서 이동합니다.그러나 에너지 흐름의 크기와 방향은 일반 물질과 NIM 모두에서 기본적으로 동일합니다.에너지 흐름은 두 재료(미디어) 모두 동일하기 때문에 NIM의 임피던스는 RHM과 일치합니다.따라서 고유 [46][47]임피던스의 부호는 NIM에서 여전히 양의 값입니다.

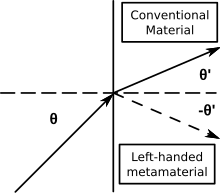
왼손잡이 재료(NIM)에 입사한 빛은 입사 빔과 같은 쪽으로 휘어지며, Snell의 법칙이 유지되려면 굴절 각도가 음수여야 합니다.수동 메타물질 매질에서 이것은 [3][46][47]굴절률의 음의 실수 및 허수 부분을 결정한다.

왼손잡이용 재료의 음굴절률

왼손 방향은 왼쪽에, 오른손 방향은 오른쪽에 표시됩니다.

1968년에 Victor Veselago의 논문은 전자파 평면파와 에너지 흐름의 반대 방향이 개별 Maxwell 컬 방정식에서 도출되었음을 보여주었다.통상광학재료에서 전계용 컬방정식은 전계E, 자기유도B, 파동전파방향에 대해 파동벡터k방향으로 가는 '오른손규칙'을 나타낸다.단, E × H에 의해 형성되는 에너지 흐름의 방향은 투과성이 0보다 클 때만 오른손잡이이다.즉, 투과성이 0보다 작을 경우(예: 음), 에너지 흐름의 방향과 반대로 파동 전파가 역전된다(k로 결정됨).또한 벡터 E, H 및 k의 관계는 "왼손잡이" 시스템을 형성하고 있으며, 현재(2011년) 널리 사용되고 있는 "왼손잡이(LH)" 재료라는 용어를 만든 것은 Veselago입니다.그는 LH 물질이 음의 굴절률을 가지고 있다고 주장했고 그의 [48]주장의 중심으로서 맥스웰 방정식의 정상 상태 해들에 의존했습니다.

30년의 공백 후, LH 물질이 마침내 입증되었을 때, 음의 굴절률의 지정은 LH 시스템에 고유한 것이라고 말할 수 있습니다. 심지어 포토닉 결정과 비교해도 마찬가지입니다.다른 많은 알려진 시스템과 마찬가지로 광자 결정도 위상 반전 및 그룹 속도와 같은 비정상적인 전파 행동을 보일 수 있습니다.그러나 이러한 시스템에서는 음의 굴절이 발생하지 않으며, 현실적으로 광결정에서는 [48][49][50]아직 발생하지 않습니다.

광주파수에서의 부굴절

광학 범위의 음의 굴절률은 2005년 샬레브 외 연구진(통신 파장 θ = 1.5 μm)[17]과 브루크 외 연구진(θ = 2 μm)에 의해 거의 [51]동시에 처음 입증되었다.

2006년, 레제크, 디온느, 앳워터가 이끄는 칼텍 팀은 가시 스펙트럼 영역에서 [52][53][54]음의 굴절을 달성했다.

역방향 체렌코프 방사선의 실험적 검증

굴절률에 대한 역치 외에도, 베셀라고는 왼손잡이 매체에서 역치 체렌코프 방사선(단순히 CR로도 알려져 있음)의 발생을 예측했다.1934년 파벨 체렌코프는 특정 매체가 빠르게 움직이는 전자빔에 의해 폭격될 때 발생하는 일관된 방사선을 발견했다.1937년 CR 주위에 구축된 이론은 전자와 같은 하전 입자가 매체의 빛의 속도보다 빠른 속도로 매체를 통과할 때 CR이 방사될 것이라고 말했습니다.CR가 발생하면 전자파가 원추형으로 방출되어 전방으로 부채꼴로 퍼져 나간다.

CR과 1937년 이론은 고에너지 물리학에서 많은 응용을 이끌어냈다.주목되는 어플리케이션은 Cherenkov 카운터입니다.이것들은 속도, 전하, 운동 방향, 에너지와 같은 하전 입자의 다양한 특성을 결정하는 데 사용됩니다.이러한 성질은 다른 입자의 식별에 중요합니다.예를 들어 카운터들은 안티프로톤과 J/medon 중간자 검출에 적용되었습니다.6개의 큰 체렌코프 카운터가 J/medon의 검출에 사용되었습니다.

거꾸로 된 체렌코프 [55][56]방사선을 실험적으로 증명하는 것은 어려웠다.

NIM을 사용하는 기타 광학 장치

수치 시뮬레이션과 함께 2000년대 초에 서브파장 포커싱을 위한 DNG 슬래브의 능력에 대한 이론적 작업이 시작되었다.이 연구는 펜드리가 제안한 "완벽한 렌즈"에서 시작되었다.펜드리 교수에 이은 여러 조사 결과 "완벽한 렌즈"는 이론적으로는 가능하지만 실용적이지 않다는 결론을 내렸다.서브파장 포커싱의 한 방향은 음지수 메타물질의 사용으로 진행되었지만 표면 플라스몬으로 이미징을 위한 강화에 기초했다.다른 방향에서는 연구자들은 NIM [3]슬래브의 근축 근사치를 조사했다.

부굴절물질의 영향

음의 굴절물질의 존재는 투과성 μ = 1의 경우 전기역학적 계산의 변화를 가져올 수 있으며, 기존의 굴절률에서 음의 값으로의 변화는 일부 특성 및 효과가 변경되었기 때문에 기존의 계산에서 부정확한 결과를 얻을 수 있다.투과율 μ의 값이 1이 아니면 스넬의 법칙, 도플러 효과, 체렌코프 복사, 프레넬의 방정식 및 페르마의 [10]원리에 영향을 미칩니다.

굴절률은 광학 과학의 기본이다.굴절률을 음의 값으로 전환하는 것은 일부 규범이나 기본 [23]법칙의 해석을 재검토하거나 재고해야 할 원인이 될 수 있다.

왼손잡이용 복합매체에 대한 미국 특허

조작된 메타물질에 대해 부여된 첫 번째 미국 특허는 "왼손 복합매체"라는 제목의 미국 특허 679만1432건이다.목록에 있는 발명가는 David R입니다. 스미스, 셸던 슐츠, 노먼 크롤, 리처드 A 셸비.

본 발명은 공통 주파수 대역에 걸쳐 음의 유전율과 투과율을 동시에 달성합니다.소재는 이미 복합적이거나 연속적인 매체를 통합할 수 있지만, 동일한 주파수 스펙트럼 내에서 음의 유전율과 투과성을 생성한다.원하는 효과를 얻기 위해 다른 유형의 연속 또는 복합물이 결합될 경우 적절한 것으로 간주될 수 있다.단, 도전성 소자의 주기적 배열을 포함하는 것이 바람직하다.어레이는 소자의 크기 및 격자 간격보다 긴 파장의 전자기 방사선을 산란합니다.어레이는 유효한 [57]미디어로 인식됩니다.

비정상적인 분산

비정상적인 분산 [58][59]매질을 통한 가우스 광펄스의 전파.그러나 정보 전송 속도는 항상 [58][60]c로 제한됩니다.

「 」를 참조해 주세요.

학술지
메타소재 서적

메모들

Public Domain이 문서에는 미국 정부의 웹사이트 또는 문서에 있는 퍼블릭 도메인 자료가 포함되어 있습니다.-NIST

  1. ^ 다음과 같은 연구 논문 그룹에서 부정적 허용치를 조사했다.
    • Pendry, J.B.; et al. (1996). "Extremely Low Frequency Plasmons in Metallic Microstructures". Phys. Rev. Lett. 76 (25): 4773–4776. Bibcode:1996PhRvL..76.4773P. doi:10.1103/physrevlett.76.4773. PMID 10061377. S2CID 35826875.

    양수 및 음수 값이 큰 효과적인 투과성을 다음 연구에서 조사했다.

레퍼런스

  1. ^ a b c d e f g h i j k l m Shelby, R. A.; Smith D.R; Shultz S. (2001). "Experimental Verification of a Negative Index of Refraction". Science. 292 (5514): 77–79. Bibcode:2001Sci...292...77S. CiteSeerX 10.1.1.119.1617. doi:10.1126/science.1058847. PMID 11292865. S2CID 9321456.
  2. ^ Sihvola, A. (2002) "메타물질의 전자기 출현: 복합매체 및 메타물질의 전자학 발전"의 3-18페이지, 복합매체 용어 분해.주디, 사이드, 시흐볼라, 아리, 아르살라네, 모하메드(에드).Kluwer Academic.ISBN 978-94-007-1067-2.
  3. ^ a b c d e f g h 문헌에서 가장 널리 사용되는 호칭은 "더블 네거티브"와 "왼손잡이"입니다.Engheta, N.; Ziolkowski, R. W. (2006). Metamaterials: Physics and Engineering Explorations. Wiley & Sons. Chapter 1. ISBN 978-0-471-76102-0.
  4. ^ a b c d Shelby, R. A.; Smith, D. R.; Shultz, S.; Nemat-Nasser, S. C. (2001). "Microwave transmission through a two-dimensional, isotropic, left-handed metamaterial" (PDF). Applied Physics Letters. 78 (4): 489. Bibcode:2001ApPhL..78..489S. doi:10.1063/1.1343489. Archived from the original (PDF) on June 18, 2010.
  5. ^ a b c d e f g h i j k l m Smith, D. R.; Padilla, Willie; Vier, D.; Nemat-Nasser, S.; Schultz, S. (2000). "Composite Medium with Simultaneously Negative Permeability and Permittivity". Physical Review Letters. 84 (18): 4184–7. Bibcode:2000PhRvL..84.4184S. doi:10.1103/PhysRevLett.84.4184. PMID 10990641.
  6. ^ a b c d e f g Veselago, V. G. (1968). "The electrodynamics of substances with simultaneously negative values of ε and μ". Soviet Physics Uspekhi. 10 (4): 509–514. Bibcode:1968SvPhU..10..509V. doi:10.1070/PU1968v010n04ABEH003699.
  7. ^ a b c d e f "Three-Dimensional Plasmonic Metamaterials". Plasmonic metamaterial research. National Institute of Standards and Technology. 20 August 2009. Retrieved 2011-01-02.
  8. ^ 마이너스 인덱스를 달성하기 위해 운용 대역폭을 늘리는 전략:
  9. ^ Boltasseva, A.; Shalaev, V. (2008). "Fabrication of optical negative-index metamaterials: Recent advances and outlook" (PDF). Metamaterials. 2 (1): 1–17. Bibcode:2008MetaM...2....1B. doi:10.1016/j.metmat.2008.03.004.
  10. ^ a b Veselago, Viktor G (2003). "Electrodynamics of materials with negative index of refraction". Physics-Uspekhi. 46 (7): 764. Bibcode:2003PhyU...46..764V. doi:10.1070/PU2003v046n07ABEH001614.
    • 대체 소스 위치:
    • Lim Hock; Ong Chong Kim; Serguei Matitsine (7–12 December 2003). Electromagnetic Materials. Proceedings of the Symposium F ((ICMAT 2003) ed.). SUNTEC, Singapore: World Scientific. pp. 115–122. ISBN 978-981-238-372-3. Victor G의 논문.베셀라고.음의 굴절률을 가진 물질의 전기역학.
  11. ^ "Caught in the "Net" Ames material negatively refracts visible light". DOE Pulse. US Department of Energy. 10 September 2007. Retrieved 2012-06-18.
  12. ^ Gibson, K. (2007). "A Visible Improvement" (PDF). Ames Laboratory. Archived from the original (PDF) on September 17, 2012. Retrieved 2012-06-18.
  13. ^ Eleftheriades, G.V.; Iyer, A.K.; Kremer, P.C. (2002). "Planar negative refractive index media using periodically L-C loaded transmission lines" (PDF). IEEE Transactions on Microwave Theory and Techniques. 50 (12): 2702. Bibcode:2002ITMTT..50.2702E. doi:10.1109/TMTT.2002.805197.
  14. ^ Iyer, A. K.; Eleftheriades, G. V. (2007). "A Multilayer Negative-Refractive-Index Transmission-Line (NRI-TL) Metamaterial Free-Space Lens at X-Band" (PDF). IEEE Transactions on Antennas and Propagation. 55 (10): 2746. Bibcode:2007ITAP...55.2746I. doi:10.1109/TAP.2007.905924. S2CID 21922234.
  15. ^ Soukoulis, C. M.; Kafesaki, M.; Economou, E. N. (2006). "Negative-Index Materials: New Frontiers in Optics" (PDF). Advanced Materials. 18 (15): 1944 and 1947. doi:10.1002/adma.200600106. S2CID 54507609.
  16. ^ Linden, S.; Enkrich, C.; Wegener, M.; Zhou, J.; Koschny, T.; Soukoulis, C. M. (2004). "Magnetic Response of Metamaterials at 100 Terahertz". Science. 306 (5700): 1351–1353. Bibcode:2004Sci...306.1351L. doi:10.1126/science.1105371. PMID 15550664. S2CID 23557190.
  17. ^ a b Shalaev, V. M.; Cai, W.; Chettiar, U. K.; Yuan, H.-K.; Sarychev, A. K.; Drachev, V. P.; Kildishev, A. V. (2005). "Negative index of refraction in optical metamaterials" (PDF). Optics Letters. 30 (24): 3356–8. arXiv:physics/0504091. Bibcode:2005OptL...30.3356S. doi:10.1364/OL.30.003356. PMID 16389830. S2CID 14917741.
  18. ^ Engheta, N. (2007). "Circuits with Light at Nanoscales: Optical Nanocircuits Inspired by Metamaterials" (PDF). Science. 317 (5845): 1698–1702. Bibcode:2007Sci...317.1698E. doi:10.1126/science.1133268. PMID 17885123. S2CID 1572047. Archived from the original (PDF) on February 22, 2012. Nader Engheta(PDF 형식)의 이 연구의 일부입니다.
  19. ^ 슬리우사 V.I.안테나 솔루션에 관한 메타물질.// 제7회 안테나 이론 및 기술 ICA 국제회의2009년 10월 6일-9일 우크라이나 리비브 TT'09 [1]페이지
  20. ^ Engheta, N.; Ziolkowski, R. W. (2005). "A positive future for double-negative metamaterials" (PDF). IEEE Transactions on Microwave Theory and Techniques. 53 (4): 1535. Bibcode:2005ITMTT..53.1535E. doi:10.1109/TMTT.2005.845188. S2CID 15293380.
  21. ^ Beruete, M.; Navarro-Cía, M.; Sorolla, M.; Campillo, I. (2008). "Planoconcave lens by negative refraction of stacked subwavelength hole arrays". Optics Express. 16 (13): 9677–9683. Bibcode:2008OExpr..16.9677B. doi:10.1364/OE.16.009677. hdl:2454/31097. PMID 18575535.
  22. ^ Alu, A.; Engheta, N. (2004). "Guided Modes in a Waveguide Filled with a Pair of Single-Negative (SNG), Double-Negative (DNG), and/or Double-Positive (DPS) Layers". IEEE Transactions on Microwave Theory and Techniques. 52 (1): 199. Bibcode:2004ITMTT..52..199A. doi:10.1109/TMTT.2003.821274. S2CID 234001.
  23. ^ a b c Shalaev, V. M. (2007). "Optical negative-index metamaterials" (PDF). Nature Photonics. 1 (1): 41. Bibcode:2007NaPho...1...41S. doi:10.1038/nphoton.2006.49. S2CID 170678.
  24. ^ a b c d Liu, H.; Liu, Y. M.; Li, T.; Wang, S. M.; Zhu, S. N.; Zhang, X. (2009). "Coupled magnetic plasmons in metamaterials" (PDF). Physica Status Solidi B. 246 (7): 1397–1406. arXiv:0907.4208. Bibcode:2009PSSBR.246.1397L. doi:10.1002/pssb.200844414. S2CID 16415502. Archived from the original (PDF) on June 24, 2010.
  25. ^ Ulaby, Fawwaz T.; Ravaioli, Umberto. Fundamentals of Applied Electromagnetics (7th ed.). p. 363.
  26. ^ Pendry, J. B. (2004). "A Chiral Route to Negative Refraction". Science. 306 (5700): 1353–5. Bibcode:2004Sci...306.1353P. doi:10.1126/science.1104467. PMID 15550665. S2CID 13485411.
  27. ^ Tretyakov, S.; Nefedov, I.; Shivola, A.; Maslovski, S.; Simovski, C. (2003). "Waves and Energy in Chiral Nihility". Journal of Electromagnetic Waves and Applications. 17 (5): 695. arXiv:cond-mat/0211012. doi:10.1163/156939303322226356. S2CID 119507930.
  28. ^ Plum, E.; Zhou, J.; Dong, J.; Fedotov, V. A.; Koschny, T.; Soukoulis, C. M.; Zheludev, N. I. (2009). "Metamaterial with negative index due to chirality" (PDF). Physical Review B. 79 (3): 035407. Bibcode:2009PhRvB..79c5407P. doi:10.1103/PhysRevB.79.035407. S2CID 119259753.
  29. ^ Zhang, S.; Park, Y.-S.; Li, J.; Lu, X.; Zhang, W.; Zhang, X. (2009). "Negative Refractive Index in Chiral Metamaterials". Physical Review Letters. 102 (2): 023901. Bibcode:2009PhRvL.102b3901Z. doi:10.1103/PhysRevLett.102.023901. PMID 19257274.
  30. ^ a b c d Padilla, W.J.; Smith, D. R.; Basov, D. N. (2006). "Spectroscopy of metamaterials from infrared to optical frequencies" (PDF). Journal of the Optical Society of America B. 23 (3): 404–414. Bibcode:2006JOSAB..23..404P. doi:10.1364/JOSAB.23.000404. Archived (PDF) from the original on 2011-06-04.
  31. ^ a b "Physicists invent "left-handed" material". Physicsworld.org. Institute of Physics. 2000-03-24. p. 01. Retrieved 2010-02-11.
  32. ^ Shelby, R. A.; Smith, D. R.; Schultz, S. (2001). "Experimental verification of a negative index of refraction". Science. 292 (5514): 77–79. Bibcode:2001Sci...292...77S. CiteSeerX 10.1.1.119.1617. doi:10.1126/science.1058847. JSTOR 3082888. PMID 11292865. S2CID 9321456.
  33. ^ a b c McDonald, Kim (2000-03-21). "UCSD Physicists Develop a New Class of Composite Material with 'Reverse' Physical Properties Never Before Seen". UCSD Science and Engineering. Retrieved 2010-12-17.
  34. ^ Program contact: Carmen Huber (2000-03-21). "Physicist Produce Left Handed Composite Material". National Science Foundation. Retrieved 2009-07-10.
  35. ^ Ma, Hyungjin (2011). "An Experimental Study of Light-Material Interaction at Subwavelength Scale" (PDF). PhD Dissertation. MIT. p. 48. Retrieved January 23, 2012.
  36. ^ Cho, D.J.; Wu, Wei; Ponizovskaya, Ekaterina; Chaturvedi, Pratik; Bratkovsky, Alexander M.; Wang, Shih-Yuan; Zhang, Xiang; Wang, Feng; Shen, Y. Ron (2009-09-28). "Ultrafast modulation of optical metamaterials". Optics Express. 17 (20): 17652–7. Bibcode:2009OExpr..1717652C. doi:10.1364/OE.17.017652. PMID 19907550. S2CID 8651163.
  37. ^ Chaturvedi, Pratik (2009). "Optical Metamaterials: Design, Characterization and Applications" (PDF). PhD Dissertation. MIT. p. 28. Retrieved January 23, 2012.
  38. ^ Pennicott, Katie (2001-04-05). "Magic material flips refractive index". Physics World. Institute of Physics. Retrieved 2010-02-12.
  39. ^ Bill Casselman (2009). "The Law of Refraction". University of British Columbia, Canada, Department of Mathematics. Retrieved 2009-07-06.
  40. ^ Taylor, L.S. (2009). "An Anecdotal History of Optics from Aristophanes to Zernike". University of Maryland; Electrical Engineering Department. Retrieved 2009-07-07.
  41. ^ Ward, David W.; Nelson, Keith A; Webb, Kevin J (2005). "On the physical origins of the negative index of refraction". New Journal of Physics. 7 (213): 213. arXiv:physics/0409083. Bibcode:2005NJPh....7..213W. doi:10.1088/1367-2630/7/1/213. S2CID 119434811.
  42. ^ Pendry, J.B.; Holden, A.J.; Robbins, D.J.; Stewart, W.J (1999). "Magnetism from conductors and enhanced nonlinear phenomena" (PDF). IEEE Transactions on Microwave Theory and Techniques. 47 (11): 2075–2084. Bibcode:1999ITMTT..47.2075P. CiteSeerX 10.1.1.564.7060. doi:10.1109/22.798002. Archived from the original (PDF) on 2011-07-17. Retrieved 2009-07-07.
  43. ^ "Radar types, principles, bands, hardware". Weather Edge Inc. 2000. Archived from the original on 2012-07-17. Retrieved 2009-07-09.
  44. ^ Parazzoli, C.G.; et al. (2003-03-11). "Experimental Verification and Simulation of Negative Index of Refraction Using Snell's Law" (PDF). Physical Review Letters. 90 (10): 107401 (2003) [4 pages]. Bibcode:2003PhRvL..90j7401P. doi:10.1103/PhysRevLett.90.107401. PMID 12689029. Archived from the original (PDF download available to the public.) on July 19, 2011.
  45. ^ Pacheco, J.; Grzegorczyk, T.; Wu, B.-I.; Zhang, Y.; Kong, J. (2002-12-02). "Power Propagation in Homogeneous Isotropic Frequency-Dispersive Left-Handed Media" (PDF). Phys. Rev. Lett. 89 (25): 257401 (2002) [4 pages]. Bibcode:2002PhRvL..89y7401P. doi:10.1103/PhysRevLett.89.257401. PMID 12484915. Archived from the original (PDF download is available to the public.) on May 24, 2005. Retrieved 2010-04-19.
  46. ^ a b Caloz, C.; et al. (2001-12-01). "Full-wave verification of the fundamental properties of left-handed materials in waveguide configurations" (PDF). Journal of Applied Physics. 90 (11): 5483. Bibcode:2001JAP....90.5483C. doi:10.1063/1.1408261. Retrieved 2009-12-29.
  47. ^ a b Ziolkowski, Richard W; Ehud Heyman (2001-10-30). "Wave propagation in media having negative permittivity and permeability" (PDF). Physical Review E. 64 (5): 056625. Bibcode:2001PhRvE..64e6625Z. doi:10.1103/PhysRevE.64.056625. PMID 11736134. Archived from the original (PDF) on July 17, 2010. Retrieved 2009-12-30.
  48. ^ a b Smith, David R.and; Norman Kroll (2000-10-02). "Negative Refractive Index in Left-Handed Materials" (PDF). Physical Review Letters. 85 (14): 2933–2936. Bibcode:2000PhRvL..85.2933S. doi:10.1103/PhysRevLett.85.2933. PMID 11005971. Archived from the original (PDF) on July 19, 2011. Retrieved 2010-01-04.
  49. ^ Srivastava, R.; et al. (2008). "Negative refraction by Photonic Crystal" (PDF). Progress in Electromagnetics Research B. 2: 15–26. doi:10.2528/PIERB08042302. Archived from the original (PDF) on July 19, 2010. Retrieved 2010-01-04.
  50. ^ Abo-Shaeer, Jamil R. (July 2010). "Negative-Index Materials". DARPA – Defense Science Offices (DSO). Archived from the original (Public Domain – Information presented on the DARPA Web Information Service is considered public information and may be distributed or copied. Use of appropriate byline/photo/image credits is requested.) on 2010-12-24. Retrieved 2010-07-05. {{cite web}}:외부 링크 format=(도움말)
  51. ^ 를 클릭합니다.
  52. ^ Caltech Media Relations.가시광선의 음굴절이 실증되어 2010년 6월 1일 웨이백 머신에 보관된 클로킹 디바이스로 이어질 수 있습니다.2007년 3월 22일 접속일– 2010-05-05
  53. ^ PhysOrg.com (April 22, 2010). "Novel negative-index metamaterial that responds to visible light designed" (Web page). Retrieved 2010-05-05.
  54. ^ Dillow, Clay (April 23, 2010). "New Metamaterial First to Bend Light in the Visible Spectrum" (Web page). Popular Science. Retrieved 2010-05-05.[데드링크]
  55. ^ Xi, Sheng; et al. (2009-11-02). "Experimental Verification of Reversed Cherenkov Radiation in Left-Handed Metamaterial". Phys. Rev. Lett. 103 (19): 194801 (2009). Bibcode:2009PhRvL.103s4801X. doi:10.1103/PhysRevLett.103.194801. hdl:1721.1/52503. PMID 20365927. S2CID 1501102.
  56. ^ Zhang, Shuang; Xiang Zhang (2009-11-02). "Flipping a photonic shock wave". Physics. 02 (91): 03. Bibcode:2009PhyOJ...2...91Z. doi:10.1103/Physics.2.91.
  57. ^ Smith, David; Schultz, Sheldon; Kroll, Norman; Shelby, Richard A. "좌측 복합 미디어" 미국 특허 6,791,432 발행일 2001-03-16, 발행일 2004-03-14.
  58. ^ a b Dolling, Gunnar; Christian Enkrich; Martin Wegener; Costas M. Soukoulis; Stefan Linden (2006). "Simultaneous Negative Phase and Group Velocity of Light in a Metamaterial". Science. 312 (5775): 892–894. Bibcode:2006Sci...312..892D. doi:10.1126/science.1126021. PMID 16690860. S2CID 29012046.
  59. ^ Garrett, C. G. B.; D. E. McCumber (1969-09-25). "Propagation of a Gaussian Light Pulse through an Anomalous Dispersion Medium" (PDF). Phys. Rev. A. 1 (2): 305–313. Bibcode:1970PhRvA...1..305G. doi:10.1103/PhysRevA.1.305.[영구 데드링크]
  60. ^ Stenner, M. D.; Gauthier, D. J.; Neifeld, M. A. (Oct 2003). "The speed of information in a 'fast-light' optical medium". Nature. 425 (6959): 695–8. Bibcode:2003Natur.425..695S. doi:10.1038/nature02016. PMID 14562097. S2CID 4333338.

추가 정보

외부 링크