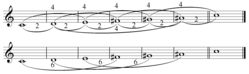
인터벌 벡터
Interval vector
음악 집합 이론에서 간격 벡터는 피치 클래스의 집합에 존재하는 간격을 요약하는 자연수의 배열이다. (즉, 옥타브가 무시되는 투구 세트) 다른 이름으로는 IC 벡터(또는 구간 클래스 벡터), PIC 벡터(또는 피치 클래스 간격 벡터), APIC 벡터(또는 절대 피치 클래스 간격 벡터)[1]: 48 가 있다.
주로 분석 도구인 반면에 간격 벡터는 다른 피치 등급의 집합에 의해 만들어지는 음질을 빠르게 보여주기 때문에 작곡가들에게도 유용할 수 있다. 즉, 관습적으로 불협화음 구간(초와 7초)이 고농도인 집합은 불협화음으로 들리는 반면, 관습적으로 불협화음 구간(즉, 3초와 6초)이 더 많은 집합은 더 많은 자음으로 들린다. 조화와 부조화에 대한 실제 인식은 레지스터와 같은 많은 문맥적 요인을 포함하지만, 그럼에도 불구하고 구간 벡터는 유용한 도구가 될 수 있다.
정의
12음 동일 기질에서 인터벌 벡터는 6자리 숫자를 가지며, 각 숫자는 집합에 인터벌 클래스가 나타나는 횟수를 나타낸다. 구간 클래스가 사용되기 때문에 집합의 순열이나 수직 배열에 관계없이 주어진 집합의 구간 벡터는 동일하게 유지된다. 각 자릿수에 의해 지정된 간격 클래스는 왼쪽에서 오른쪽으로 상승한다. 즉,
- 단초/주요 7초(1 또는 11세미턴)
- 주요 초/초과 7초(2 또는 10세미턴)
- 3분의 1/주요 6분의 1(3 또는 9세미턴)
- 3/3/4학년 6반(4 또는 8세미턴)
- 완전 4/완벽한 5분위(5 또는 7세미턴)
- 트리톤(6세미톤) (트리톤은 역방향으로 자신과 동일하다.)
유니언과 옥타브를 나타내는 인터벌 클래스 0은 생략된다.
하워드 핸슨은 1960년 저서 『현대 음악의 조화』에서 이 개념에 대한 단일한 표기법을 도입하였는데, 이 개념은 현재 contentabcdef에 쓰여질 내용을 pmnedc.sdt라고baf 명명하였다. 알렌 포르테가[when?][citation needed] 도입한 현대식 표기법은 상당한 장점을 가지고[specify] 있으며 옥타브의 어떤 균등한 분할에도 확장 가능하다.
인터벌 벡터가 6개의 고유 자릿수를 갖는 척도는 딥 스케일 속성을 갖는다고 한다. 주요 규모와 그 모드는 이러한 특성을 가지고 있다.
실제적인 예로 루트 위치의 C장삼각형(3-11B)에 대한 간격 벡터(Play(Help·info))
는 ⟨001110⟩이다. 즉, 세트가 하나의 주요한 3분의 1 또는 마이너 6위(즉, C에서 E로, 또는 G에서 E로, 또는 G에서 E로), 하나의 마이너 3분의 1 또는 메이저 6위(즉, C에서 G로, 또는 G에서 C로) 또는 완벽한 4위(즉, C에서 G에서 C로)를 가지는 것을 의미한다. 인터벌 벡터는 전위 또는 역전에 따라 변하지 않으므로 전체 세트 등급에 속하는데, 이는 ⟨001110⟩은 모든 주요(및 마이너) 트라이애드의 벡터라는 뜻이다. 어떤 간격 벡터는 다른 것을 생산하기 위해 전이되거나 반전될 수 없는 둘 이상의 집합에 해당한다.(이러한 것을 아래에서 설명하는 Z 관련 집합이라고 한다.)
n 피치 클래스 집합의 경우 집합의 간격 벡터에 있는 모든 숫자의 합은 삼각 numberTn−1 = n × (n − 1)/2.
데이빗 르윈의 '일반화된 음악적 간격과 변환'에서 설명한 대로 변환 이론에도 확장된 형태의 인터벌 벡터가 사용된다.[full citation needed]
Z 관계
음악 세트 이론에서, 이항 관계라고도 불리는 Z-관계는 두 세트가 동일한 인터뷰적 내용(따라서 동일한 인터벌 벡터)을 가지지만, 두 세트가 (다른 T-타입의n) 전이적으로 관련되거나 (다른n T/TI-타입의n) 역전적으로 관련되지 않는 두 피치 클래스 세트 사이의 관계다.[1]: 99 예를 들어, 두 세트 4-z15A {0,1,4,6} 및 4-z29A {0,1,3,7}은(는) 동일한 간격 벡터 ⟨11111⟩를 가지지만 한 세트를 다른 세트로 바꾸거나 반전시킬 수는 없다.
헥사코드의 경우 각각을 Z-헥사코드로 칭할 수 있다. "Z" 유형이 아닌 모든 헥사코드는 자체 보완물인 반면, Z-헥사코드의 보완물은 예를 들어 6-Z3와 6-Z36과 같은 Z-대응형이다.[2] 6-Z44, 6-Z17, 6-Z11 및 Forte 번호를 참조하십시오.
"zygotic"(혹은 두 생식세포의 융합)[1]: 98 Schuijer (2008), p.98 and 98n18. 이라는 용어는 1964년 알렌 포르테에서 유래했지만, 하워드 핸슨에 의해 그 개념이 처음 고려된 것 같다. 한손은 이것을 이질적 관계라고 불렀고, 이질적 관계와 같은 두 세트를 정의했다.[3] 참조: 이소머.
미치엘 슈에이저(2008)에 따르면, 어떤 피치급 보완 헥사코드라도 전환과 역전에 의해 등가물이 아니더라도 동일한 간격 벡터를 갖는다는 헥사코드 정리는 밀턴 밥빗에 의해 처음 제안되었고, "관계의 발견"은 콤프의 예로서 1960년 데이비드 르윈에 의해 "보고"되었다.리먼트 정리: 두 개의 보완적인 피치 클래스 세트에서 피치 클래스 간격의 차이가 세트들의 기본 번호 사이의 차이와 동일하다는 것(두 개의 헥사코드가 주어진다면, 이 차이는 0이다).[1]: 96–7 [4] 헥사코드 정리의 수학적 증명서는 카슬러(1961년), 리제너(1974년), 윌콕스(1983년)에 의해 발표되었다.[1]: 96–7
흔히 Z 관련 세트가 항상 쌍으로 일어나는 것이 관찰되지만, 데이비드 르윈은 이것이 12음 동일 기질(12-ET)의 결과라고 언급했다.[citation needed] 16-ET에서는 Z 관련 세트가 세 쌍둥이로 발견된다. 르윈의 제자 조나단 와일드는 상위 ET 시스템에서 최대 16명의 멤버가 있는 Z 관련 튜플릿을 찾아내며 다른 튜닝 시스템을 위해 이 작업을 계속했다.[citation needed]
사소한 등축적 경우를 허용하는 '동일한 간격 함량을 갖는 것'의 등가관계는 초기 결정학에서 연구되어 호모메트리라고 알려져 있다. 예를 들어, 보완 정리는 물리학자들에게 바비넷의 원리로 알려져 있다. 최근 설문조사는 다음을 참조하십시오.[5]
스트라우스는 "Z 관계에서 [set]은 간격 내용이 같기 때문에 비슷하게 들릴 것"[6][1]: 125 이라고 주장하는데, 이 때문에 특정 작곡가들이 작품에서 Z 관계를 이용하게 되었다. 예를 들어, {0,1,4,6}과(와) {0,1,3,7} 사이의 연극은 엘리엇 카터의 제2 현악 사중주곡에서 분명하다.[citation needed]
곱하기
일부 Z 관련 화음은 인터벌 벡터의 1과 5에 대한 동일한 항목으로 인해 M 또는 IM( 곱하기 5 또는 곱하기 7)으로 연결된다.[1]: 83, 110
참고 항목
메모들
- ^ 한손은 집합의 자음 부조화 함량을 정량화하기 위해 부조화 정도에 따라 간격을 지시하였는데, p=완벽한 5초, m=주요 3초, n=주요 3초, s=주요 초, d=(더 불협화음) 소초, t=t=트리톤이 있다.
원천
- ^ a b c d e f g h 슈에이저, 미치엘(2008) 무통 음악 분석: 피치 클래스 세트 이론과 맥락 로체스터 대학교. ISBN978-1-58046-270-9.
- ^ a b 포르테, 알렌(1977년). 무통 음악의 구조 (뉴 헤이븐과 런던: 예일 대학 출판부), 79페이지. ISBN 0-300-02120-8
- ^ 핸슨, 하워드(1960). 현대 음악의 조화 재료(뉴욕: Appleton-Century-Crofts), 22페이지. ISBN 0-89197-207-2
- ^ 르윈, 데이비드 Journal of Music Ironics 4/1(1960) : 98–101 "노트 모음의 인터뷰 내용, 노트 모음과 그 보완책: 쇤베르크의 헥사코달 작품에 대한 음악 이론 4/1: 98–101
- ^ 존 맨더로, 다니엘 기시, 에마뉘엘 아미오, 모레노 안드레타, 카를로스 아제르. 음악적 분포에서의 Z-관계와 동음계. 수학과 음악 저널, 테일러 & 프랜시스(2011), 5(2), 83-98.
- ^ 스트라우스, 조셉 네이선(1990). 포스트 토널 이론 소개, 페이지 67. 1차 개정. 프렌티스 홀: 엥글우드 클리프, 뉴저지 주. ISBN 0-13-189890-6. 슈에이저(2008)에서 인용, 페이지 125.
추가 읽기
- Ran, John(1980). 기본 무통 이론. 뉴욕: 롱맨. ISBN 9780582281172. 1987년 재판, 뉴욕: 쉬머 북스; 런던: 콜리어 맥밀런 ISBN 0-02-873160-3.
