사색 정리

수학에서, 4색 정리 또는 4색 지도 정리는 어떤 지도의 영역에도 같은 색을 칠하기 위해 4색 이하의 색이 요구되지 않는다고 말한다.인접이란 단순히 세 개 이상의 영역이 ^[1]만나는 모서리가 아니라 두 영역이 공통 경계 곡선 세그먼트를 공유한다는 것을 의미합니다.그것은 컴퓨터를 사용하여 증명된 최초의 주요 정리였다.처음에, 이 증명은 모든 수학자들에 의해 받아들여지지 않았다. 왜냐하면 컴퓨터 보조 증명은 사람이 ^[2]손으로 확인하는 것이 불가능했기 때문이다.그 증거는 그 이후로 널리 받아들여지고 있지만,^[3] 일부 의심가는 남아있다.

4색 정리는 1976년 케네스 아펠과 볼프강 하켄에 의해 많은 거짓 증명과 반례를 거쳐 증명되었다. (오색 정리와 달리, 오색 정리는 지도를 색칠하기에 충분하다는 1800년대에 증명되었다.)아펠에 대한 의문을 불식시키기 위해...같은 생각을 사용하면서도 여전히 컴퓨터에 의존하는 단순한 증거인 Haken 증거는 Robertson, Sanders, Seymour, 그리고 Thomas에 의해 1997년에 출판되었습니다.2005년, 이 정리는 또한 Georges Gonthier에 의해 범용 정리 증명 소프트웨어로 증명되었다.

정밀한 정리

그래프 이론의 관점에서, 이 정리는 루프리스 $평면{\displaystyle }$ 그래프$$G(\$displaystyle$ G$)$의 경우, 그 색수는${\displaystyle }\theta {\displaystyle }$ (${\displaystyle G)4}$4(\$displaystyle \chi (G)\leq$ 4$)$임을 나타낸다.

4가지 색정리에 대한 직관적인 진술 - "평면을 인접한 영역으로 분리할 경우, 영역은 최대 4가지 색을 사용하여 색칠할 수 있으므로 두 인접 영역이 동일한 색을 가지지 않습니다."는 정확한 설명을 위해 적절히 해석해야 합니다.

첫째, 경계 세그먼트를 공유하는 경우 영역은 인접해 있습니다.단독 경계점만 공유하는 두 영역은 인접해 있는 것으로 간주되지 않습니다.둘째, 영역이 유한하지만 둘레가 무한히 긴 것과 같은 기괴한 영역은 허용되지 않습니다. 이러한 영역이 있는 지도는 4가지 이상의 ^[4]색상을 요구할 수 있습니다(안전성을 위해 경계선이 완전히 많은 직선 세그먼트로 구성된 지역으로 제한할 수 있습니다).1개 또는 복수의 다른 지역을 완전히 둘러싸는 것은 허용됩니다.국가가 인접할 필요가 없기 때문에(예를 들어 앙골라의 일부인 카빈다 주, 아제르바이잔의 일부인 나크치반, 러시아의 일부인 칼리닌그라드, 미국의 일부가 아닌 알래스카) "인접 지역"(기술적으로는 비행기의 연결된 개방 부분 집합)의 개념은 일반 지도의 "국가"의 개념과 동일하지 않다.연속)만약 우리가 한 나라의 영토 전체를 같은 색으로 받아야 한다면, 4가지 색상으로 항상 충분하지는 않다.예를 들어 다음과 같은 간단한 맵을 생각해 보겠습니다.

이 지도에서는 A라는 라벨이 붙은2개의 지역이 같은 나라에 속해 있습니다.두 A영역이 서로 인접한 4개의 영역과 각각 인접해 있기 때문에 같은 색상을 받는다면 5가지 색상이 필요합니다.두 개의 개별 영역이 동일한 색상을 갖도록 강제하는 것은 평면 밖에서 결합하는 '핸들'을 추가하여 모델링할 수 있습니다.

이러한 구조는 임의의 지도에 대해 최대 7가지 색상을 요구하는 토러스(속 1의 표면)에 지도를 색칠하는 것과 같은 문제를 만든다.실제 지도의 수역처럼 여러 개의 분리된 영역에 단일 색상을 사용하거나 분리된 영토를 가진 국가가 더 많은 경우에도 유사한 구성이 적용된다.이러한 경우 결과 표면의 속과 함께 더 많은 색상이 필요할 수 있습니다.(아래의 「개요」섹션을 참조해 주세요).

더 간단한 정리 서술은 그래프 이론을 사용한다.지도의 영역 집합은 각 영역에 대한 정점과 경계 세그먼트를 공유하는 모든 영역 쌍에 대한 모서리가 있는 무방향 그래프로 보다 추상적으로 나타낼 수 있습니다.이 그래프는 평면입니다.각 정점을 대응하는 영역 내에서 임의로 선택한 위치에 배치하고 공유 경계 세그먼트를 넘어 인접 영역의 정점으로 이어지는 교차 없는 곡선으로 모서리를 그리면 교차 없이 평면에 그릴 수 있습니다.반대로 어떤 평면 그래프도 이와 같이 지도에서 형성할 수 있다.그래프 이론 용어에서, 4색 정리는 모든 평면 그래프의 정점에 최대 4색까지 색을 입힐 수 있으며, 따라서 인접한 두 정점에 동일한 색을 입히지 않거나 짧게는 다음과 같은 색을 입힐 수 없음을 나타냅니다.

모든 평면 그래프는 ^[5]4색입니다.

역사

조기 실증 시도

알려진 ^[6]한, 이 추측은 1852년 ^[7]10월 23일 프란시스 거스리가 영국의 카운티 지도에 색을 입히려고 노력하던 중 4가지 색깔만 있으면 된다는 것을 알아차렸을 때 처음 제안되었다.당시 구트리의 형 프레데릭은 런던 유니버시티 칼리지의 아우구스투스 드 모건(프란시스의 전 고문)의 제자였다.프란시스는 프레데릭에게 그것에 대해 물어봤고, 그는 그것을 드 모건에게 가져갔다.De Morgan에 따르면:

"거트리의 한 학생이 제가 사실인지 몰랐던 사실에 대해 이유를 대달라고 했습니다.그는 도형이 어느 정도 분할되어 있고 구획의 색이 달라 공통 경계선의 어떤 부분을 가진 도형이 다른 색상으로 되어 있다면 (4가지 색상은 필요하지만 그 이상은 필요 없다) 다음과 같은 경우라고 말합니다.Query는 5개 이상을 발명할 필요가 없습니다.(Wilson 2014, 페이지 18)

"F.G."는 아마도 ^[8]두 구트리스 중 한 명으로 1854년 아테네에 그 질문을 실었고,^[9] 드 모건은 1860년 같은 잡지에 그 질문을 다시 제기했다.아서 케일리(1879)가 초기에 출판한 또 다른 언급은 그 추측을 드 모건 탓으로 돌린다.

그 정리를 증명하기 위한 몇 번의 초기 실패 시도가 있었다.De Morgan은 4개 지역에 대한 단순한 사실에서 따랐다고 믿었지만, 그 사실이 더 기본적인 사실에서 파생될 수 있다고는 생각하지 않았다.

이것은 다음과 같은 방법으로 발생합니다.4개의 카운티가 존재하지 않는 한 4개의 컬러는 필요 없습니다.각 카운티는 다른 3개의 카운트와 같은 경계선을 가지고 있습니다.하나 이상의 지역이 다른 지역에 의해 기울어지지 않는 한 4개 지역에서는 이러한 일이 일어날 수 없습니다. 따라서 기울어진 카운티에 사용되는 색은 자유롭게 사용할 수 있습니다.4개의 영역이 다른 3개의 영역과 공통의 경계를 가질 수 없다는 이 원칙은 보다 명확하고 기초적인 것을 증명할 수 있는 것이 아니라 가정으로 ^[9]서 있어야 합니다.

제안된 증거 중 하나는 1879년 알프레드 켐페에 의해 발표되었고,^[10] 다른 하나는 1880년 피터 거스리 타이트에 의해 발표되었습니다.1890년이 되어서야 퍼시 호우드에 의해 켐프의 증거가 부정확하게 나타났고, 1891년 줄리어스 피터슨에 의해 타이트의 증거가 부정확하게 나타났는데, 각각의 거짓 증거는 11년 ^[11]동안 아무런 문제 없이 서있었다.

1890년, 켐페의 증거의 결함을 드러내는 것 외에도, 호우드는 오색 정리를 증명했고 사색 추측을 임의의 ^[12]속 표면으로 일반화했다.

1880년, Tait는 4색 정리가 특정 유형의 그래프(현대 용어로는 스나크라고 함)는 반드시 ^[13]평면이 아닌 것이어야 한다는 진술과 동등하다는 것을 보여주었다.

1943년, Hugo Hadwiger는 아직도 풀리지 않은 4색 문제의 광범위한 일반화인 Hadwiger ^[14]추측을 공식화했다.

컴퓨터에 의한 증명

1960년대와 1970년대에 독일의 수학자 하인리히 헤슈는 증거를 찾기 위해 컴퓨터를 사용하는 방법을 개발했다.특히 그는 정리를 증명하기 위해 방전을 최초로 사용했는데, 이는 후속 아펠의 피할 수 없는 부분에서 중요한 것으로 밝혀졌다.해켄 프루프.그는 또한 환원성의 개념을 확장하여 Ken Durre와 함께 이를 위한 컴퓨터 테스트를 개발했습니다.불행히도 이 중대한 시기에 그는 일을 ^[15]계속하기 위해 필요한 슈퍼컴퓨터의 시간을 확보할 수 없었다.

다른 사람들은 그의 컴퓨터 보조 방식을 포함하여 그의 방식을 따랐다.다른 수학자들이 증명하기 위해 경쟁하는 동안, 일리노이 대학의 케네스 아펠과 볼프강 하켄은 1976년 ^[16]6월 21일 그들이 정리를 증명했다고 발표했다.그들은 John A의 알고리즘 작업에 도움을 받았다. 코흐^[15]

4가지 색상의 추측이 거짓이라면 5가지 색을 필요로 하는 지역 수가 최소인 맵이 적어도 1개 있을 것입니다.증거는 다음과 같은 두 가지 기술적 ^[17]개념을 사용하여 그러한 최소한의 반례가 존재할 수 없다는 것을 보여주었다.

1. 피할 수 없는 집합은 최소한의 4색 삼각측량(최소도 5를 갖는 등)이 되기 위해 필요한 조건을 충족하는 모든 맵이 이 집합에서 적어도1개의 구성을 가져야 하는 구성 집합이다.
2. 축소 가능한 구성은 최소한의 반례로는 발생할 수 없는 국가의 배열이다.맵에 축소 가능한 구성이 포함되어 있는 경우 맵을 더 작은 맵으로 축소할 수 있습니다.이 작은 지도는 4가지 색상으로 색칠할 수 있으면 오리지널 지도에도 적용할 수 있다는 조건이 붙어 있습니다.즉, 원래 맵을 4가지 색상으로 색칠할 수 없는 경우 더 작은 맵도 색칠할 수 없으므로 원래 맵은 최소가 아닙니다.

축소 가능한 구성의 특성에 기초한 수학적 규칙과 절차를 사용하여 Appel과 Haken은 피할 수 없는 축소 가능한 구성의 집합을 찾았고, 따라서 4가지 색상의 추측에 대한 최소한의 반례가 존재할 수 없음을 증명했습니다.그들의 증거는 가능한 지도의 무한함을 1,834개의 축소 가능한 구성(나중에 1,482개로 줄임)으로 줄였고, 이 구성들은 컴퓨터로 하나씩 확인해야 했고 천 시간 이상이 걸렸다.이 작업의 축소 가능 부분은 서로 다른 프로그램 및 컴퓨터에서 독립적으로 두 번 확인되었습니다.그러나 증명의 불가피한 부분은 하켄의 딸 도로테아 블로스테인의 도움을 받아 손으로 확인해야 하는 400페이지 이상의 마이크로피쉬에서 확인되었습니다(Apel & Haken 1989).

아펠과 하켄의 발표는 전 세계 언론에 의해 널리 보도되었고 일리노이 대학 수학과는 "4가지 색상으로 충분합니다"라고 적힌 소인을 사용했다.이와 동시에, 광범위한 컴퓨터 지원을 통해 증명된 최초의 주요 정리이며, 사람이 검증할 수 있는 부분의 복잡성은 상당한 논란을 불러일으켰다(Wilson 2014).

1980년대 초, Appel에 결함이 있다는 소문이 퍼졌다.해켄 프루프.RWTH Aachen의 Ulrich Schmidt는 1981년에 발표된 석사 논문의 아펠과 하켄의 증명을 조사했다(Wilson 2014, 225).그는 피치 못할 부분을 약 40% 확인했고 퇴원 절차에서 중대한 오류를 발견했다(Appel & Haken 1989).1986년, 아펠과 하켄은 Mathemical Intelligence의 편집자로부터 그들의 증거에 결함이 있다는 소문을 다루는 기사를 써달라는 요청을 받았다.그들은 루머가 "[슈미트의] 결과에 대한 잘못된 해석 때문"이라고 답했고 상세한 기사에 감사했다(윌슨 2014, 225–226).그들의 매그넘 오퍼스, Every Planel Map is Four-Colorable은 완전하고 상세한 증거(400페이지 이상의 마이크로피시 보충본 포함)를 주장하는 책이다.그 책은 슈미트에 의해 발견된 오류와 다른 사람들에 의해 발견된 몇 가지 추가 오류를 설명하고 수정했다(Appel & Haken 1989).

심플화와 검증

정리가 증명된 이후 O(n²) 시간만을 필요로 하는 4색 맵에 대해 효율적인 알고리즘이 발견되었으며, 여기서 n은 정점의 수이다.1996년 닐 로버트슨, 다니엘 P. 샌더스, 폴 시모어, 로빈 토마스는 2차 시간 알고리즘을 만들어 아펠과 하켄의 ^[18]증명에 기초한 4차 시간 알고리즘을 개선했다.이 새로운 증명은 Appel 및 Haken과 비슷하지만 문제의 복잡성을 줄이고 축소 가능한 구성을 633개만 체크하면 되기 때문에 효율적입니다.이 새로운 증거의 불가피성과 환원성 부분은 모두 컴퓨터로 실행되어야 하며 ^[19]손으로 확인하는 것은 비현실적입니다.2001년, 같은 저자들이 스나크 ^[20]추측을 증명함으로써 대안 증거를 발표했다.그러나 이 증거는 아직 공개되지 않았다.

2005년, Benjamin Werner와 Georges Gonthier는 Coq 증명 조교 안에서 정리의 증명을 공식화했다.이것에 의해, 특정의 케이스를 검증하기 위해서 사용되는 다양한 컴퓨터 프로그램을 신뢰할 필요가 없어졌습니다.Coq ^[21]커널만 신뢰하면 됩니다.

실증 아이디어의 개요

다음 설명은 Every Planel Map is Four Colorable(1989년 애플 & Haken) 소개에 기초한 요약입니다.결점은 있었지만, 4색 정리에 대한 켐프의 원래 증명은 나중에 그것을 증명하기 위해 사용된 몇 가지 기본적인 도구들을 제공했다.여기서의 설명은 위의 현대 그래프 이론 공식의 관점에서 다시 표현된다.

켐프의 주장은 다음과 같다.첫째, 그래프에 의해 분리된 평면 영역이 삼각 측량되지 않은 경우, 즉 경계에 정확히 세 개의 가장자리가 없는 경우, 무한 외부 영역을 포함한 모든 영역을 삼각형으로 만들기 위해 새로운 정점을 도입하지 않고 모서리를 추가할 수 있다.이 삼각형 그래프가 네 가지 색상 이하로 색칠이 가능한 경우 모서리를 제거하면 동일한 색상이 적용되므로 원래 그래프도 색칠이 가능합니다.따라서 삼각 그래프에 대한 4색 정리를 증명하면 모든 평면 그래프에 대해 증명하고 일반성의 손실 없이 그래프가 삼각 그래프라고 가정합니다.

v, e 및 f가 정점, 모서리 및 영역(면)의 수라고 가정합니다.각 영역은 삼각형이고 각 가장자리는 두 영역에서 공유되므로 2e = 3f가 됩니다.이 값을 오일러 공식 v - e + f = 2와 함께 사용하여 6v - 2e = 12임을 나타낼 수 있습니다.정점의 정도는 정점에 접하는 모서리의 수입니다.v가 n도의 정점 수이고 D가 모든 정점의 최대 도수일 경우_n,

${\displaystyle 6v-2e=6\sum _{i=1}^{D}v_{i}-\sum _{i=1}^{D}iv_{i}=\sum _{i=1}^{D}(6-i)v_{i}=12.}$

그러나 모든 i 6 6에 대해 12 > 0 및 6 - i 0 0이므로, 이것은 5도 이하의 정점이 적어도 하나 있다는 것을 나타낸다.

5가지 색상이 필요한 그래프가 있는 경우, 그러한 그래프는 최소이며, 정점을 제거하면 4가지 색상이 됩니다.이 그래프를 G라고 합니다.그러면 G는 3도 이하의 정점을 가질 수 없습니다. 왜냐하면 d(v) 3 3이면 G에서 v를 제거하고 작은 그래프로 4색칠한 다음 다시 v를 추가하고 인접 그래프와 다른 색상을 선택하여 4색칠을 확장할 수 있기 때문입니다.

Kempe는 또한 G가 4도의 꼭지점을 가질 수 없다는 것을 정확하게 보여주었다.이전과 마찬가지로 정점 v를 제거하고 나머지 정점에 4가지 색을 입힙니다.v의 4개의 인접 라우터가 모두 다른 색상(예: 빨간색, 녹색, 파란색 및 노란색)인 경우 빨간색과 파란색 인접 라우터를 연결하는 빨간색과 파란색의 정점 경로를 찾습니다.이러한 경로를 켐페 체인이라고 합니다.빨간색과 파란색 이웃을 연결하는 켐프 체인이 있을 수 있고 녹색과 노란색 이웃을 연결하는 켐프 체인이 있을 수 있지만, 둘 다 있을 수 없습니다. 왜냐하면 이 두 경로가 반드시 교차하고 교차하는 정점은 색칠할 수 없기 때문입니다.체인으로 연결되어 있지 않은 것이 빨간색과 파란색 네이버라고 가정합니다.빨간색과 파란색의 교대 경로를 통해 빨간색 인접 장치에 연결된 모든 정점을 탐색한 다음 이러한 모든 정점의 색상을 빨간색과 파란색으로 바꿉니다.결과는 여전히 유효한 4가지 색상으로, 이제 v를 다시 추가하고 빨간색으로 색칠할 수 있습니다.

이것은 G가 꼭짓점이 5인 경우만 남지만, Kempe의 주장은 이 경우에 결함이 있었다.Hewood는 Kempe의 실수를 알아채고, 만약 5가지 색깔만 있으면 된다는 것을 증명하는 것에 만족한다면, 위의 주장(최소한의 반례가 6가지 색을 요구한다는 것만 변경)을 통해 5가지 상황에서 Kempe 체인을 사용하여 5가지 색깔 정리를 증명할 수 있다는 것을 관찰했다.

어떤 경우에도 이 정도 5 정점의 경우를 다루기 위해서는 정점을 제거하는 것보다 더 복잡한 개념이 필요합니다.오히려 인수의 형식은 G의 각 정점의 정도(G)와 연결된 하위 그래프인 구성을 고려하는 것으로 일반화된다.예를 들어, 도수 4의 정점 상황에서 기술된 경우는 G의 도수 4를 갖는 것으로 라벨이 붙은 단일 정점으로 구성된 구성입니다. 위와 같이 구성이 제거되고 나머지 그래프가 4색일 경우 구성이 다시 추가될 때 색칠이 변경되는 것으로 충분합니다.e 4 소켓도 확장할 수 있습니다.이것이 가능한 설정을 리듀서블 설정이라고 부릅니다.설정 세트 중 적어도1개가 G 내의 어딘가에서 발생할 필요가 있는 경우, 그 세트는 피할 수 없는 것이라고 불립니다.위의 논의는 피할 수 없는 5가지 구성의 집합(도 1의 단일 정점, 도 2, ...의 단일 정점, 도 5의 단일 정점)을 주는 것으로 시작되었고, 이어서 첫 번째 4가 환원 가능하다는 것을 보여주었습니다; 집합의 모든 구성이 환원 가능한 경우, 피할 수 없는 구성 집합을 나타내기 위해정리.

G는 삼각형이므로 구성 내의 각 정점의 정도를 알 수 있고 구성 내부의 모든 엣지를 알 수 있으며, 주어진 구성에 인접한 G의 정점 수는 고정되어 있으며, 이들은 사이클로 결합되어 있다.이러한 정점은 설정의 링을 형성합니다.링에 k개의 정점이 있는 설정은 k링 설정이며 링과 함께 링 설정이라고 불립니다.위의 간단한 예와 같이 링의 고유한 4가지 색상을 모두 열거할 수 있습니다. 구성의 색상을 변경하지 않고 확장할 수 있는 모든 색상을 처음에는 양호하다고 합니다.예를 들어 네이버가 3개 이하인 위의 싱글버텍스 설정은 처음에는 양호했습니다.일반적으로 링의 색상을 양호한 색으로 바꾸려면 링의 주변 그래프를 체계적으로 기억해야 합니다. 위의 경우 4개의 네이버가 있습니다.따라서 링이 큰 일반 구성의 경우 보다 복잡한 기술이 필요합니다.링의 4가지 색상의 구별이 많기 때문에, 이것은 컴퓨터의 지원이 필요한 주된 순서입니다.

마지막으로, 이 절차로 줄일 수 있는 피할 수 없는 구성 세트를 식별하는 것이 남습니다.이러한 집합을 발견하는 데 사용되는 주요 방법은 방전 방법입니다.방전의 기초가 되는 직관적인 아이디어는 평면 그래프를 전기 네트워크로 간주하는 것입니다.처음에는 양전하와 음전하가 정점 사이에 분배되어 합계가 양전하가 됩니다.

위의 수식을 기억해 주세요.

$\displaystyle \sum _{i=1}^{D}(6-i)v_{i}=12.}$

각 정점에는 6-deg(v)의 초기 전하가 할당된다.그런 다음 방전 절차인 규칙 집합에 따라 정점에서 인접 정점으로 체계적으로 전하를 재배포함으로써 전하를 "유동"시킵니다.전하가 보존되어 있기 때문에, 일부 정점은 여전히 양의 전하를 가지고 있습니다.규칙에서는 양의 하전된 정점의 설정 가능성을 제한하기 때문에 가능한 모든 설정을 열거하면 피할 수 없는 집합이 됩니다.

피할 수 없는 세트의 일부 부재를 줄일 수 없는 한, 배출 절차는 (다른 구성을 도입하는 동안) 제거하도록 수정됩니다.Appel과 Haken의 최종 배출 절차는 매우 복잡했으며, 결과적으로 피할 수 없는 구성 세트에 대한 설명과 함께 400페이지 분량의 볼륨을 채웠지만 생성된 구성은 기계적으로 확인할 수 있어 줄일 수 있었다.피할 수 없는 구성 세트 자체를 설명하는 볼륨을 확인하는 작업은 몇 년에 걸쳐 피어 리뷰를 통해 수행되었습니다.

여기서 설명하지는 않지만 증명을 완료하기 위해 필요한 기술적 세부사항은 침지 감소성입니다.

거짓 반증

사색정리는 오랜 역사 속에서 많은 거짓 증명과 반증을 끌어내는 것으로 악명이 높다.처음에 뉴욕타임스는 정책상 애플에 대한 보도를 거부했다.Haken의 증명은 이전과 같이 거짓으로 나타날까 두려워한다(Wilson 2014).위에 언급된 켐페와 테이트와 같은 일부 증거들은 반박되기 전에 10년 이상 대중의 감시를 받았다.하지만 아마추어에 의해 쓰여진 많은 책들은 전혀 출판되지 않았다.

일반적으로 가장 단순한 반례는 무효이지만 다른 모든 영역에 접하는 하나의 영역을 생성하려고 시도합니다.이렇게 하면 나머지 영역이 3가지 색상만으로 색칠됩니다.4색 정리가 사실이기 때문에, 이것은 항상 가능하다; 그러나 지도를 그리는 사람이 하나의 큰 영역에 초점을 맞추고 있기 때문에, 그들은 나머지 지역이 사실 3색상으로 칠해질 수 있다는 것을 알아차리지 못한다.

이 방법은 일반화할 수 있다.일부 지역의 색을 미리 선택하면 나머지 지역의 색을 칠할 수 없게 되는 지도가 많다.반례의 일반적인 검증자는 이러한 지역의 색을 바꿀 생각을 하지 않을 수 있으며, 따라서 반례가 유효한 것처럼 보일 수 있습니다.

아마도 이러한 일반적인 오해를 뒷받침하는 한 가지 효과는 색상 제한이 과도적이지 않다는 사실일 것이다. 즉, 한 지역은 직접 접촉하는 지역과 색칠을 달리하면 되는 것이지 접촉하는 지역에 접촉하는 것은 아니다.이것이 제한사항이라면 평면 그래프는 임의로 많은 색상을 필요로 할 것이다.

다른 잘못된 반증들은 여러 개의 분리된 부분으로 구성된 영역을 사용하거나 같은 색상의 영역이 한 점에서 접촉하는 것을 허용하지 않는 것과 같은 정리의 가정에 위배된다.

삼색

모든 평면 지도는 4가지 색상으로 색칠할 수 있지만, 임의의 평면 지도를 3가지 ^[22]색상으로 색칠할 수 있는지 여부는 복잡도 면에서 NP-완전입니다.

입방체 지도는 각 내부 영역이 짝수인 인접 ^[23]영역을 가지고 있는 경우에만 3가지 색상으로 색칠할 수 있습니다.미국의 주 지도 예에서 육지로 둘러싸인 미주리(MO)에는 8개의 이웃(짝수)이 있습니다.모든 이웃과 다른 색을 사용해야 하지만 이웃은 색을 바꿀 수 있기 때문에 지도의 이 부분에는 3가지 색상만 필요합니다.그러나 육지로 둘러싸인 네바다(NV)에는 5개의 이웃(홀수)이 있습니다. 즉, 이웃 중 하나는 이웃과 다른 모든 이웃과 서로 다른 색이어야 합니다. 따라서 여기에는 4가지 색이 필요합니다.

일반화

무한 그래프

4색 정리는 유한 평면 그래프뿐만 아니라 평면에 교차하지 않고 그릴 수 있는 무한 그래프에도 적용되며, 더 일반적으로 모든 유한 부분 그래프가 평면인 무한 그래프(아마도 셀 수 없는 수의 정점이 있는)에도 적용됩니다.이를 증명하기 위해 무한 그래프의 모든 유한 서브그래프가 k-색깔이 가능하다면 전체 그래프도 k-색깔이 가능한 내쉬-윌리엄(1967)이라는 De Bruijn-Erd's 정리와 유한 평면 그래프에 대한 정리의 증명을 결합할 수 있다.이것은 1차 논리에 대한 Kurt Gödel의 콤팩트성 정리의 즉각적인 결과로 볼 수 있습니다.단순히 논리 공식 세트를 사용하여 무한 그래프의 색채성을 표현합니다.

높은 표면

평면 ^[24]이외의 표면의 착색 문제도 생각할 수 있습니다.구체 또는 실린더의 문제는 평면의 문제와 동일합니다.양의 속성을 가진 닫힌(방향성 또는 방향성이 없는) 표면의 경우, 필요한 최대 색상 수 p는 다음 공식에 따라 표면의 오일러 특성에 따라 달라집니다.

${{displaystyle p=\left\lfloor}{frac {7+{\fracrt {49-24\chi}}{2}}\right\loor,}$

여기서 가장 바깥쪽 브래킷은 바닥 기능을 나타냅니다.

또는 배향 가능한 표면에 대해 표면의 속(g:

${{displaystyle p=\left\lfloor}{frac {7+{\fracrt {1+48g}}{2}}\right\loor.}$

이 공식, Hewood 추측은 1890년 P. J. Hewood에 의해 제안되었고, 몇몇 사람들의 기고 끝에 1968년 Gerhard Ringel과 J. W. T. Youngs에 의해 증명되었다.이 공식의 유일한 예외는 클라인 병으로, 오일러 특성이 0이지만(이 공식은 p = 7을 나타내지만), 1934년 필립 프랭클린에 의해 보여지듯이 6가지 색상만을 필요로 한다.

예를 들어, 토러스는 오일러 특성 θ = 0(및 g = 1)을 가지며, 따라서 p = 7을 가지므로 토러스 상의 지도를 색칠하는 데 7개 이상의 색상이 필요하지 않다.이 상한 7은 날카롭다: Szilassi 다면체와 같은 특정 트로이덜 다면체는 7가지 색상을 필요로 한다.

뫼비우스 스트립은 1평면 그래프(가장자리에 최대 1개의 단순 교차로 그려진 그래프)와 마찬가지로 6가지 색상(Tietze 1910)이 필요하다(Borodin 1984).평면 그래프의 정점과 면이 모두 같은 색을 띠지 않는 방식으로 착색된 경우(Borodin 1984), 다시 최대 6가지 색상이 필요하다.

• 

  반지름 대칭인 7색 토러스 – 같은 색상의 영역이 점선을 따라 감겨 있습니다.

• 

  8색 이중 토러스(일반 2개 표면) – 기포는 두 영역의 고유한 조합을 나타냅니다.

• 

  6색 클라인 병

• 

  Tietze는 Möbius 스트립을 6개의 서로 인접한 영역으로 분할하여 6개의 색상을 필요로 합니다.분할의 꼭지점과 가장자리는 띠에 Tietze 그래프를 포함합니다.

• 

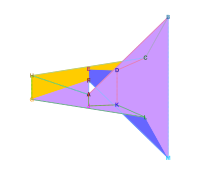
  7개의 면이 서로 인접한 대화형 Szilassi 다면체 모델 - SVG 이미지에서 마우스를 움직여 회전시킵니다.

• 

  필요한 색상의 수가 3차원 이상에서 제한되지 않는다는 증거

솔리드 영역

3차원 입체영역에 대한 착색 결과의 확장은 없습니다.n개의 플렉시블 로드 세트를 사용하면 모든 로드가 다른 로드와 접촉하도록 배치할 수 있습니다.세트는 n가지 색상 또는 모든 막대와 접촉하는 빈 공간을 포함하여 n+1이 필요합니다.숫자 n은 원하는 만큼 큰 정수입니다.이러한 예는 1880년 프레드릭 거스리에 의해 알려졌다(윌슨 2014).축 평행 입방체(2개의 입방체가 2차원 경계 영역을 공유하는 경우 인접하는 것으로 간주됨)에서도 무한의 색상이 필요할 수 있습니다(Red & Allwright 2008; Magnant & Martin (2011).

수학의 다른 영역과의 관계

드로르 바르 나탄은 리 대수와 바실리예프 불변량에 관한 진술을 했는데, 이는 4색 ^[25]정리에 해당한다.

수학 이외에서 사용

국가의 정치적 지도를 색칠한 동기에도 불구하고, 이 정리는 지도 제작자들에게 특별한 관심이 없다.수학사학자 케네스 메이의 기사에 따르면, "4가지 색상만을 사용하는 지도는 드물고, 보통 3가지 색상만 사용하는 지도는 3가지 색상만 필요합니다.지도 제작과 지도 제작사에 관한 책에는 4색 특성에 대한 언급이 없다.(윌슨 2014, 2)이 정리는 또한 동일한 국가의 비인접 지역(예: 알래스카와 미국의 나머지 지역)이 동일한 색으로 칠해지는 일반적인 지도 제작 요건을 보장하지 않는다.

「 」를 참조해 주세요.

• 아폴로 네트워크
• 오색 정리
• 그래프 색칠
• 그뢰츠의 정리: 삼각형이 없는 평면 그래프는 3색이다.
• Hadwiger-Nelson 문제: 단위 거리에서 떨어진 두 점이 같은 색을 가지지 않도록 평면을 색칠하는 데 몇 가지 색상이 필요합니까?

메모들

레퍼런스

외부 링크

• "Four-colour problem", Encyclopedia of Mathematics, EMS Press, 2001 [1994]

• MathOverflow의 4색 정리 일반화 목록