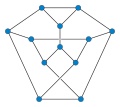
티에체 그래프
Tietze's graph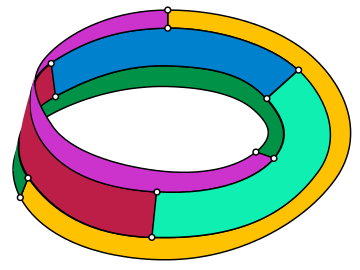
| 티에체 그래프 | |
|---|---|
 티에체 그래프 | |
| 정점 | 12 |
| 가장자리 | 18 |
| 반지름 | 3 |
| 지름 | 3 |
| 둘레 | 3 |
| 자동형성 | 12 (D6) |
| 색수 | 3 |
| 색도 지수 | 4 |
| 특성. | 큐빅 스나크 |
| 그래프 및 모수 표 | |
그래프 이론의 수학적 분야에서 티에체 그래프는 12 정점과 18개의 가장자리를 가진 비방향 입방 그래프다.1910년 뫼비우스 띠를 모두 만지는 6개 영역(스트립의 경계를 따라 3개, 중심선을 따라 3개)으로 세분할 수 있다는 것을 보여준 하인리히 프란츠 프리드리히 티에체(Heinrich Franzh Friedrich Tietze)의 이름을 따서 명명되었다.[1]티에체 소분부(Möbius 스트립 자체의 경계를 따라 분할된 부분 포함)의 경계 부분은 티에체 그래프를 내장한다.
Petersen 그래프와의 관계
티에체 그래프는 피터슨 그래프에서 정점 중 하나를 삼각형으로 대체함으로써 형성될 수 있다.[2][3]티에체 그래프와 마찬가지로 피터슨 그래프는 상호 접촉하는 6개의 영역의 경계를 형성하지만 뫼비우스 스트립보다는 투영면에 있다.하나의 꼭지점을 둘러싸고 있는 돌출면의 이 구획에서 구멍을 자르는 경우, 둘러싸인 꼭지점은 이전에 설명한 티에체 그래프의 구성을 제공하면서 구멍 주위의 지역 경계 삼각형으로 대체된다.
해밀턴시티
Tietze의 그래프와 Petersen 그래프 모두 최대 비 해밀턴계 그래프인데, 해밀턴계 주기는 없지만, 두 개의 비인접 정점들은 해밀턴계 경로로 연결될 수 있다.[2]Tietze의 그래프와 Petersen 그래프는 정점이 12개 이하인 유일하게 2Vertex로 연결된 해밀턴 이외의 입방체 그래프다.[4]
피터슨 그래프와는 달리, 티에체 그래프는 저자극이 아니다: 세 개의 삼각형 꼭지점 중 하나를 제거하면 해밀턴이 아닌 것으로 남아 있는 더 작은 그래프를 형성한다.
엣지 컬러링과 완벽한 매치
테이지 컬러링 티에츠의 그래프는 4가지 색상이 필요하다. 즉, 색지수는 4이다.동등하게, 티에체 그래프의 가장자리는 4개의 일치로 분할할 수 있지만 그 이하가 아니다.
Tietze의 그래프는 스나크의 정의의 일부와 일치한다: 그것은 3-엣지 색상이 아닌 입방체 브리지리스 그래프다.그러나 대부분의 저자는 3주기 없이 스네이크를 그래프에 제한하기 때문에 티에체 그래프는 일반적으로 스네이크로 간주되지 않는다.그럼에도 불구하고, 그것은 R에 의해 소개된 꽃 스나크의 무한 계열의 일부인 그래프 J에3 이형적이다. 1975년 아이작스.[5]
피터슨 그래프와는 달리, 티에체 그래프는 네 개의 완벽한 일치로 덮을 수 있다.이 속성은 그래프를 네 번의 완벽한 일치로 커버할 수 있는지 테스트하는 것이 NP-완전하다는 증거에 핵심적인 역할을 한다.[6]
추가 속성
Tietze의 그래프는 색도 번호 3, 색도 지수 4, 둘레 3, 지름 3을 가지고 있다.독립번호는 5번이다.그것의 자동형 집단은 순서 12를 가지며, 회전과 반사를 모두 포함한 육각형의 대칭 집단인 이음계 집단6 D에 대해 이형성이다.이 그룹은 정점에 3 크기의 궤도와 6 크기의 궤도의 궤도를 가지고 있으며, 따라서 이 그래프는 정점이 아니다.
갤러리
| 위키미디어 커먼즈에는 티에체 그래프와 관련된 미디어가 있다. |
참고 항목
메모들
- ^ Tietze, Heinrich (1910), "Einige Bemerkungen zum Problem des Kartenfärbens auf einseitigen Flächen" [Some remarks on the problem of map coloring on one-sided surfaces], DMV Annual Report, 19: 155–159[permanent dead link].
- ^ a b Clark, L.; Entringer, R. (1983), "Smallest maximally nonhamiltonian graphs", Periodica Mathematica Hungarica, 14 (1): 57–68, doi:10.1007/BF02023582
- ^ Weisstein, Eric W. "Tietze's Graph". MathWorld.
- ^ Punnim, Narong; Saenpholphat, Varaporn; Thaithae, Sermsri (2007), "Almost Hamiltonian cubic graphs" (PDF), International Journal of Computer Science and Network Security, 7 (1): 83–86
- ^ Isaacs, R. (1975), "Infinite families of nontrivial trivalent graphs which are not Tait colorable", Amer. Math. Monthly, Mathematical Association of America, 82 (3): 221–239, doi:10.2307/2319844, JSTOR 2319844.
- ^ Esperet, L.; Mazzuoccolo, G. (2014), "On cubic bridgeless graphs whose edge-set cannot be covered by four perfect matchings", Journal of Graph Theory, 77 (2): 144–157, arXiv:1301.6926, doi:10.1002/jgt.21778, MR 3246172.