This is a good article. Click here for more information.

방향 아세클릭 그래프

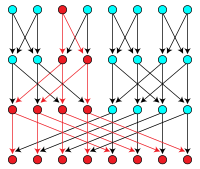
Directed acyclic graph
지시된 반복 그래프 예제

수학, 특히 그래프 이론, 컴퓨터 과학에서 지시된 악순환 그래프(DAG 또는 dag /ˈd dag // 오디오 스피커 아이콘(듣기))는 지시된 사이클이 없는 지시된 그래프다.즉, 그것은 정점과 가장자리(arcs라고도 함)로 구성되며, 각 가장자리는 한 꼭지점에서 다른 꼭지점으로 향하며, 따라서 그러한 방향을 따르는 것은 결코 닫힌 루프를 형성하지 않는다.방향 그래프는 정점을 모든 에지 방향과 일치하는 선형 순서로 배열하여 위상적으로 순서가 가능한 경우에만 DAG이다.DAG는 생물학(진화, 가계수, 역학)부터 사회학(초대 네트워크), 계산(스케줄링)에 이르기까지 수많은 과학 및 계산 응용 프로그램을 가지고 있다.

정의들

그래프는 꼭지점과 꼭지점 쌍을 연결하는 가장자리에 의해 형성되며, 여기서 꼭지점은 가장자리별로 쌍으로 연결된 어떤 종류의 물체가 될 수 있다.지시된 그래프의 경우 각 가장자리에는 한 꼭지점에서 다른 꼭지점까지의 방향이 있다.지시된 그래프의 경로는 시퀀스에서 각 에지의 끝 정점이 다음 에지의 시작 정점과 동일한 속성을 갖는 가장자리의 시퀀스로, 첫 에지의 시작 정점이 마지막 에지의 끝 정점과 같으면 경로가 사이클을 형성한다.방향 아세클릭 그래프는 사이클이 없는 방향 그래프다.[1][2][3]

방향 그래프의 꼭지점 v는 u에서 시작하여 v에서 끝나는 경로가 있을 때 다른 꼭지점 u에서 도달할 수 있다고 한다. 특별한 경우, 모든 꼭지점은 그 자체에서 도달할 수 있는 것으로 간주된다(가장자리가 0인 경로).정점이 비경쟁 경로(가장자리가 하나 이상 있는 경로)를 통해 자신에게 도달할 수 있는 경우, 그 경로는 순환이기 때문에 지시된 반복 그래프를 정의하는 또 다른 방법은 비경쟁 경로를 통해 정점이 스스로 도달할 수 없는 그래프라는 것이다.[4]

수학적 특성

도달성 관계, 전이성 폐쇄 및 전이성 감소

A DAG
그것의 전이적 감소

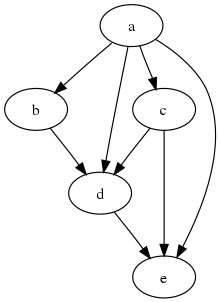
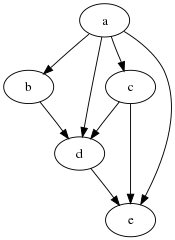
DAG의 도달 가능성 관계는 DAG의 정점에 부분 순서 ≤으로 공식화할 수 있다.이 부분적인 순서에서, 두 개의 꼭지점 u와 v는 정확히 DAG에 u에서 v까지의 방향 경로가 존재할 때 u ≤ v로 주문된다.[5] 즉, u에서 v에 도달할 수 있을 때(또는 u에서 v에 도달할 수 있을 때)그러나 서로 다른 DAG는 동일한 도달 가능성 관계와 동일한 부분 질서를 발생시킬 수 있다.[6]예를 들어, 두 개의 가장자리 u → v → v → v → w → w → w → w의 접근성 관계는 세 개의 가장자리 u → v → w → w → w → w → w의 DAG와 동일하다. 이 두 DAG는 정점이 u v v ≤ w와 동일한 부분 순서를 생성한다.

DAG의 Transitive closure는 DAG와 동일한 도달 가능성 관계를 갖는 가장 에지를 가진 그래프다.DAG의 도달 가능성 관계 ≤에서 모든 꼭지점 쌍(u, v)에 대해 에지 u → v를 가지고 있으므로 도달성 관계를 그래프-이론적 용어로 직접 번역하는 것으로 생각할 수 있다.부분순서를 DAG로 변환하는 동일한 방법이 보다 일반적으로 작용한다: 유한 부분순서 집합(S, ≤)마다, ≤의 모든 원소의 정점과 verte의 모든 원소 쌍에 대한 에지를 갖는 그래프는 자동으로 전적으로 닫힌 DAG이며, 도달성 관계로서 (S, ≤)를 가지고 있다.이러한 방식으로 모든 유한 부분 순서 집합을 DAG로 나타낼 수 있다.

3개 요소 집합의 하위 집합 중 세트 포함(초과)의 부분 순서를 나타내는 Hasse 다이어그램

DAG의 transitive 감소는 DAG와 동일한 도달 가능성 관계를 가진 가장 적은 에지를 가진 그래프다.DAG의 도달 가능성 관계 ≤에 대한 커버 관계에서 모든 꼭지점 쌍(u, v)에 대해 에지 u → v를 가진다.이는 DAG의 하위그래프로, DAG가 u에서 v로 가는 더 긴 방향 경로를 포함하고 있는 u → v를 위해 생성된다. transitive closure와 마찬가지로 transitive closure는 DAG에 대해 고유하게 정의된다.이와는 대조적으로, 지시된 그래프의 경우, 동일한 도달 가능성 관계를 가진 최소 하위 그래프가 둘 이상 있을 수 있다.[7]타동성 감소는 동일한 순서를 나타내는 다른 그래프에 비해 가장자리가 적고 따라서 그래프 도면이 단순하기 때문에 그들이 나타내는 부분 순서를 시각화하는 데 유용하다.부분 순서의 Hasse 다이어그램은 가장자리의 시작 정점을 끝 정점보다 낮은 위치에 배치하여 모든 가장자리의 방향이 표시되는 전이적 감소를 그린 것이다.[8]

위상 순서

지시된 반복 그래프의 위상학적 순서: 모든 가장자리는 순서 초반(왼쪽 위)부터 순서 후반(오른쪽 아래)까지입니다.지시된 그래프는 위상학적 순서가 있는 경우에만 반복된다.
빨간색 가장자리를 파란색 방향의 순환 그래프에 추가하면 파란색 그래프의 전이성 폐쇄인 또 다른 DAG가 생성된다.각 빨간색 또는 파란색 에지 u → v에 대해 u에서 v에 도달할 수 있음: u에서 시작하여 v에서 끝나는 파란색 경로가 있음.

지시된 그래프의 위상학적 순서는 모든 가장자리에서 가장자리의 시작 정점이 가장자리의 끝 정점보다 더 빨리 발생하도록 그 정점을 시퀀스로 정렬하는 것이다.위상학적 순서가 있는 그래프는 사이클의 초기 꼭지점까지의 가장자리는 잘못된 방향으로 향해야 하기 때문에 사이클을 가질 수 없다.따라서 위상학적 순서가 있는 모든 그래프는 반복적이다.반대로 모든 지시된 반복 그래프는 적어도 하나의 위상학적 순서가 있다.따라서 위상학적 순서의 존재는 지시된 반복 그래프의 등가 정의로 사용될 수 있다. 즉, 위상학적 순서가 정확히 있는 그래프들이다.[2]일반적으로 이 순서는 고유하지 않다. DAG는 모든 정점을 포함하는 방향 경로를 가진 경우에만 고유한 위상학적 순서가 있으며, 이 경우 순서는 경로에 정점이 나타나는 순서와 동일하다.[9]

DAG의 위상학적 순서 집합은 DAG에 대한 도달 가능성 관계의 선형 확장 집합과 동일하므로 동일한 부분 순서를 나타내는 두 개의 그래프는 동일한 위상학적 순서 집합을 가진다.[10]

콤비네이터 열거

지시된 반복 그래프를 세는 그래프 열거 문제는 로빈슨(1973)에 의해 연구되었다.[11]n = 0, 1, 2, 3 …에 대해 (이 숫자가 DAG의 위상학적 순서에 나타나는 순서에 제한이 없는) 정점 n에 대한 DAG의 수는 다음과 같다.

1, 1, 3, 3, 25, 543, 29281, 3781503, … (OEIS의 경우 시퀀스 A003024).

이 숫자는 반복 관계에 의해 계산될 수 있다.

[11]

Eric W. Weisstein과 McKay 등이 추측했다.[12] (2004) 동일한 숫자가 모든 고유값이 양의 실수인 (0,1) 행렬을 계산한다는 것을 증명했다.증거는 비거주적이다: 행렬 A는 A + I가 모든 고유값을 갖는 (0,1) 행렬인 경우에만 DAG의 인접 행렬이다. 여기서 나는 ID 행렬을 나타낸다.DAG는 자체 루프를 가질 수 없으므로 인접 행렬은 0 대각선이어야 하므로, 추가하면 모든 행렬 계수가 0 또는 1인 속성을 보존한다.[13]

관련 그래프 패밀리

다중 트리, 하위 그래프가 모든 꼭지점에서 도달할 수 있는 DAG(예: 빨간색)
폴리 트리, 방향 지정되지 않은 트리의 가장자리 방향을 지정하여 형성된 DAG

다중 트리(강력하게 모호하지 않은 그래프 또는 맹그로브라고도 함)는 두 꼭지점 사이에 최대 하나의 방향 경로가 있는 DAG이다.동등하게, 그것은 어떤 꼭지점에서든 도달할 수 있는 서브그래프가 비방향 트리를 유도하는 DAG이다.[14]

폴리트리(poly tree, directed tree라고도 함)는 비방향 트리의 가장자리 방향을 정하여 형성된 다중 트리다.[15]

수목은 비방향 트리의 가장자리를 특정 꼭지점에서 멀리 향하게 하여 형성된 폴리 트리로, 수목의 뿌리라고 한다.

계산 문제

위상 분류 및 인식

주요 기사:위상 분류

위상학적 정렬은 주어진 DAG의 위상학적 순서를 찾는 알고리즘 문제다.그것은 선형 시간 안에 해결될 수 있다.[16]위상학적 정렬을 위한 칸의 알고리즘은 정점 순서를 직접 만든다.그것은 부분적으로 구성된 위상학적 순서에 아직 포함되지 않은 다른 정점으로부터 들어오는 가장자리가 없는 정점들의 목록을 유지한다; 처음에 이 목록은 들어오는 가장자리가 전혀 없는 정점으로 구성된다.그런 다음 부분적으로 구성된 위상학적 순서 끝에 이 리스트의 꼭지점 하나를 반복적으로 추가하고, 그 리스트에 이웃을 추가해야 하는지 여부를 확인한다.알고리즘은 모든 정점이 이런 방식으로 처리되면 종료된다.[17]또는 깊이 첫 번째 검색 그래프 통과의 사후 주문 번호 지정을 반대로 하여 위상학적 순서를 구성할 수 있다.[16]

또한 지정된 그래프는 DAG 선형 시간에의 위상 순서 찾기가 결과 순서 또는 대안 valid[18]은 각 가장자리, 어떤 위상 구분 알고리즘이 들지 않고도 알고리즘 성공적으로 주문 모든 vertices을 확인함으로써 시험 시도에 의해 확인한다.eting 오류 [17]조건

순환 그래프를 사용한 구조

모든 비방향 그래프는 정점에 대한 전체 순서를 선택하고 이전 끝점에서 이후 끝점으로 모든 가장자리를 지시하여 DAG로 만들 수 있다.그 결과 가장자리의 방향은 순환 방향이라고 불린다.다른 총 순서에 따라 동일한 순환 방향이 나올 수 있으므로 n-vertex 그래프는 n! 순환 방향보다 작을 수 있다.반복 방향의 수는 χ(-1)과 같다. 여기서 χ은 주어진 그래프의 색다형 다항식이다.[19]

노란색 방향의 악순환 그래프는 파란색 방향 그래프의 응결이다.그것은 파란색 그래프의 강하게 연결된 각 구성요소를 하나의 노란색 꼭지점으로 수축시킴으로써 형성된다.

모든 방향 그래프는 모든 사이클에 접촉하는 정점 또는 에지 세트(존중적으로)인 피드백 정점 세트 또는 피드백 호 세트를 제거하여 DAG로 만들 수 있다.그러나 그러한 집합 중 가장 작은 집합은 찾기 어려운 NP이다.[20]임의로 지시된 그래프는 각각의 강하게 연결된 구성요소를 단일 수퍼버텍스로 수축시킴으로써 응결이라고 불리는 DAG로 변환될 수도 있다.[21]그래프가 이미 반복된 경우 가장 작은 피드백 정점 집합과 피드백 호 집합은 비어 있고, 그 응축은 그래프 그 자체다.

Transitive closure and transitive Red

정점과 m 가장자리가 있는 특정 DAG의 전이성 폐쇄는 각 꼭지점으로부터의 도달성을 테스트하기 위해 너비 우선 검색 또는 깊이 우선 검색을 사용하여 시간 O(mn)으로 구성될 수 있다.[22]또는 Ω < 2.373은 매트릭스 곱셈 알고리즘의 지수인 시간 O(nω)에서 해결할 수 있다. 이는 밀도 그래프의 O(mn)에 대한 이론적 개선이다.[23]

이러한 모든 전이성 폐쇄 알고리즘에서 길이 2 이상의 한 경로로 도달할 수 있는 정점 쌍과 길이 1 경로로만 연결할 수 있는 쌍을 구별할 수 있다.transitive 감소는 그들의 끝점을 연결하는 유일한 경로인 길이 하나의 경로를 형성하는 가장자리로 구성된다.따라서, 전이성 감소는 전이성 폐쇄와 동일한 점근성 시간 범위로 구성될 수 있다.[24]

마감문제

주요 기사:마감문제

폐쇄 문제는 정점 가중치 방향 AC 순환 그래프를 입력하는 것으로 간주하며, 가장자리가 C를 떠나지 않는 정점 C의 집합인 폐쇄의 최소(또는 최대) 중량을 찾는다.이 문제는 지시된 그래프에 대해 반복성을 가정하지 않고 공식화될 수 있지만 더 큰 일반성은 없다. 이 경우 그래프의 응축에 대한 동일한 문제와 동일하기 때문이다.최대 흐름 문제의 감소를 이용하여 다항식 시간에 해결할 수 있다.[25]

경로 알고리즘

위상학적 순서의 원리에 기초하여 일반 그래프 대신 DAG에 사용할 때 일부 알고리즘은 더 단순해진다.예를 들어, 위상학적 순서로 정점을 처리하고, 각 정점에 대한 경로 길이를 들어오는 가장자리를 통해 얻은 최소 길이 또는 최대 길이가 되도록 계산함으로써 선형적으로 DAG의 지정된 시작 정점에서 최단 경로와 긴 경로를 찾을 수 있다.[26]대조적으로 임의 그래프의 경우 최단 경로에는 Dijkstra 알고리즘이나 Bellman-Ford 알고리즘과 같은 느린 알고리즘이 필요할 수 있으며 임의 그래프에서 가장 긴 경로는 찾기 어려운 NP-hard이다.[27][28]

적용들

스케줄링

부분 순서의 지시된 반복 그래프 표현은 순서 제약이 있는 작업 시스템의 스케줄링에 많은 응용 프로그램을 가지고 있다.[29]셀 중 하나를 변경한 후 스프레드시트의 셀 또는 소스 코드가 변경된 후 컴퓨터 소프트웨어의 오브젝트 파일 등 업데이트해야 하는 개체의 컬렉션을 다루는 유형의 중요한 문제 클래스.이 맥락에서, 종속성 그래프는 업데이트할 각 객체에 대한 정점 및 두 객체를 서로 다른 객체보다 빨리 업데이트해야 할 때마다 연결하는 가장자리가 있는 그래프다.이 그래프에서 사이클은 순환 종속성이라고 하며, 사이클과 관련된 작업을 일관성 있게 스케줄링할 수 있는 방법이 없기 때문에 일반적으로 허용되지 않는다.순환 종속성이 없는 종속성 그래프는 DAG를 형성한다.[30]

예를 들어 스프레드시트의 한 셀이 변경되면 변경된 셀에 직접 또는 간접적으로 의존하는 다른 셀의 값을 다시 계산할 필요가 있다.이 문제에 대해, 스케줄링할 작업은 스프레드시트의 개별 셀 값을 재계산하는 것이다.의존성은 한 셀의 식이 다른 셀의 값을 사용할 때 발생한다.이 경우 사용되는 값은 이를 사용하는 식보다 먼저 다시 계산해야 한다.종속성 그래프를 토폴로지 순서로 정렬하고 이 위상학적 순서를 사용하여 셀 업데이트를 예약하면 셀당 하나의 평가만으로 전체 스프레드시트를 업데이트할 수 있다.[31]프로그램 컴파일을[31] 위한 make files와 낮은 수준의 컴퓨터 프로그램 최적화를 위한 명령 스케줄링에서도 유사한 작업 순서 문제가 발생한다.[32]

5개의 이정표(10-50으로 표시됨)와 6개의 과제(A-F로 표시됨)가 있는 프로젝트에 대한 PERT 관리도.ADF와 BC의 두 가지 중요한 경로가 있다.

DAG의 최초 적용 사례 중 하나였던 대규모 인적 프로젝트의 관리 방법인 프로그램 평가 및 검토 기법(PERT)에 의해 다소 다른 DAG 기반 스케줄링 제약의 공식화가 사용된다.이 방법에서 DAG의 정점은 수행할 특정 태스크가 아닌 프로젝트의 이정표를 나타낸다.대신 작업이나 활동은 작업의 시작과 완료를 표시하는 두 개의 이정표를 연결하는 DAG의 가장자리로 표현된다.각 가장자리에는 작업 팀이 작업을 수행하는 데 걸리는 시간의 추정치가 붙어 있다.이 DAG에서 가장 긴 경로는 프로젝트의 임계 경로, 즉 프로젝트의 총 시간을 제어하는 경로를 나타낸다.개별 마일스톤은 그 정점에서 끝나는 가장 긴 경로의 길이에 따라 예약될 수 있다.[33]

데이터 처리 네트워크

처리 요소의 네트워크를 나타내기 위해 지시된 반복 그래프를 사용할 수 있다.이 표현에서 데이터는 유입되는 가장자리를 통해 처리 요소를 입력하며 소자는 나가는 가장자리를 통해 남는다.

예를 들어 전자 회로 설계에서 정적 결합 논리 블록은 입력의 함수를 계산하는 로직 게이트의 AC순환 시스템으로 표현될 수 있으며, 여기서 함수의 입력과 출력은 개별 비트로 표현된다.일반적으로 이러한 블록의 출력은 그것의 반복적인 속성을 유지하는 레지스터나 상태 요소에 의해 포착되지 않는 한 입력으로 사용될 수 없다.[34]종이 또는 데이터베이스에 있는 전자 회로 도표는 인스턴스(instance) 또는 구성요소를 사용하여 하위 수준 구성요소에 대한 지시 참조를 형성하는 지시된 반복 그래프의 한 형태다.전자 회로 자체는 반드시 순환하거나 방향을 지시하는 것은 아니다.

데이터 흐름 프로그래밍 언어는 데이터 스트림에 대한 운영 시스템과 일부 운영의 출력과 다른 운영의 입력 사이의 연결을 설명한다.이러한 언어는 반복적인 데이터 처리 작업을 기술하는데 편리할 수 있으며, 이 작업에서 반복적으로 연결된 동일한 작업 컬렉션이 많은 데이터 항목에 적용된다.그것들은 병렬 알고리즘으로 실행될 수 있다. 병렬 프로세스에 의해 각 연산을 수행하는 병렬 알고리즘으로서 다른 입력 세트가 이용 가능하게 되는 즉시.[35]

컴파일러에서 직선 코드(즉, 루프나 조건부 분기 없는 문장의 시퀀스)는 코드 내에서 수행된 각 산술 연산의 입력과 출력을 설명하는 DAG로 나타낼 수 있다.이러한 표현을 통해 컴파일러는 공통적인 하위표현 제거를 효율적으로 수행할 수 있다.[36]더 높은 수준의 코드 조직에서, 순환 종속성 원칙은 큰 소프트웨어 시스템의 모듈이나 구성요소들 사이의 의존성이 지시된 순환 그래프를 형성해야 한다고 명시한다.[37]

피드포워드 신경망은 또 다른 예다.

인과구조

주요 기사:베이시안 네트워크

정점이 일정한 시간에 발생하는 이벤트를 나타내는 그래프와 가장자리가 항상 가장자리의 초기 정점부터 늦은 시간 정점까지 점인 그래프는 반드시 방향을 잡고 반복한다.주기의 부족은 그래프의 어떤 경로를 따라갈수록 항상 정점 관련 시간이 증가하기 때문에 경로의 정점으로 되돌아갈 수 없기 때문이다.이것은 인과관계가 사건이 미래에만 영향을 미칠 수 있고, 그것들은 결코 과거에 영향을 미치지 않으며, 따라서 우리는 인과 루프를 가지고 있지 않다는 우리의 자연스러운 직관을 반영한다.이러한 유형의 유도 반복 그래프의 예로는 양자 중력에 대한 인과 집합 접근방식에서 마주친 그래프들이 있지만, 이 경우 고려된 그래프는 실제로 완전하다.버전 기록 예제에서 소프트웨어의 각 버전은 일반적으로 버전을 저장, 커밋 또는 릴리스한 시간인 고유한 시간과 연관되어 있다.인용 그래프의 경우 문서는 한 번에 발행되며 오래된 문서만 참조할 수 있다.

때때로 이벤트는 특정 물리적 시간과 연관되지 않는다.사건 쌍이 사건들 사이의 인과 관계를 나타내는 순수한 인과 관계를 가지고 있다면, 우리는 지시된 반복 그래프를 가질 것이다.[38]예를 들어, 베이지안 네트워크는 DAG의 이전 가능성으로부터 사건의 가능성이 계산될 수 있는 지시된 순환 그래프에서 정점으로 확률론적 사건 시스템을 나타낸다.[39]이러한 맥락에서 DAG의 도덕적 그래프는 동일한 정점의 모든 부모 사이에 (비방향) 가장자리를 추가한 다음(때로는 결혼이라고도 함) 모든 지시된 가장자리를 비방향 가장자리로 대체함으로써 생성된 비방향 그래프다.[40]유사한 인과 구조를 가진 다른 유형의 그래프는 영향 다이어그램으로, 이 그래프의 정점은 의사결정을 나타내거나 알 수 없는 정보를 나타내며, 가장자리는 한 꼭지점에서 다른 꼭지점으로 인과적 영향을 나타낸다.[41]예를 들어 역학에서 이러한 도표는 개입에 대한 다른 선택의 예상 가치를 추정하는 데 종종 사용된다.[42][43]

그 반론도 사실이다.지시된 반복 그래프에 의해 대표되는 적용에 인과 구조가 존재하는데, 예시에서의 명시적 순서나 시간 또는 그래프 구조에서 파생될 수 있는 순서가 그것이다.이는 모든 방향의 반복 그래프에는 위상학적 순서가 있기 때문에, 즉 모든 가장자리가 그 순서를 따라 동일한 방향을 가리키도록 정점을 순서에 넣는 방법이 적어도 한 가지 있기 때문이다.

계보 및 버전 이력

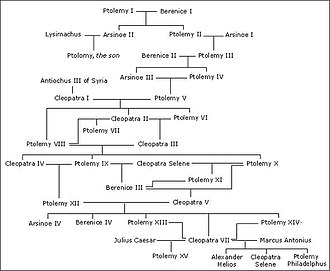
프톨레마이오스 왕조의 가계도인데, 가까운 친척들 사이에 결혼이 많아 혈통이 무너진다.

패밀리 트리는 각 패밀리 멤버에 대한 꼭지점 및 각 부모-자녀 관계에 대한 가장자리가 있는 지시된 순환 그래프로 볼 수 있다.[44]이름에도 불구하고, 이러한 그래프들이 반드시 나무가 되는 것은 아니다. 왜냐하면 친척들 간의 결혼 가능성 때문이다(그래서 아이는 어머니와 아버지 양쪽 모두 공통의 조상을 가지고 있다). 혈통 붕괴의 원인이 된다.[45]모계 혈통(모녀 관계)과 모계 혈통(부자 관계)의 그래프는 이 그래프 안에 있는 나무들이다.아무도 자신의 조상이 될 수 없기 때문에 가계도는 순환한다.[46]

Git와 같은 분산형 개정 제어 시스템의 버전 이력은 일반적으로 각 개정에 대한 꼭지점이 있고 서로 직접 파생된 수정 쌍을 연결하는 가장자리를 갖는 방향의 Acyclic 그래프의 구조를 가지고 있다.이것들은 일반적으로 합병으로 인한 나무가 아니다.[47]

컴퓨터 기하학의 많은 임의화된 알고리즘에서, 알고리즘은 구조물의 일련의 변화 과정에 걸쳐 기하학적 구조의 버전 이력을 나타내는 히스토리 DAG를 유지한다.예를 들어 Delaunay 삼각측량을 위한 임의 증분 알고리즘에서 각 점이 추가될 때 하나의 삼각형을 세 개의 작은 삼각형으로 교체하고, 삼각측량 쌍을 다른 쌍의 삼각형으로 교체하는 "플립" 연산에 의해 삼각측량이 변경된다.이 알고리즘의 히스토리 DAG에는 알고리즘의 일부로 구성된 각 삼각형에 대한 정점이 있으며, 각 삼각형에서 이를 대체하는 두 개 또는 세 개의 다른 삼각형까지의 가장자리가 있다.이 구조는 지점 위치 쿼리를 효율적으로 응답할 수 있게 한다: 딜라우나이 삼각측량에서 쿼리 지점 q의 위치를 찾고 기록 DAG의 경로를 따르며, q가 포함된 교체 삼각형으로 이동하는 각 단계에서.이 경로에서 도달한 최종 삼각형은 q를 포함하는 Delaunay 삼각형이어야 한다.[48]

인용 그래프

인용 그래프에서 꼭지점은 단일 발행일이 있는 문서다.가장자리는 한 문서의 참고 문헌에서 다른 필수적으로 이전 문서에 이르는 인용구를 나타낸다.그 고전적인 예는 인용 네트워크의 첫 모델인 가격 모델을 계속해서 생산한 데릭 J. 드 솔라 프라이스의 1965년 논문 "과학 논문의 네트워크"[49]에서 지적한 것처럼 학술 논문들 사이의 인용에서 나온다.[50]이 경우 논문의 인용 횟수는 인용 네트워크의 해당 꼭지점 정도일 뿐이다.이것은 인용 분석에서 중요한 조치다.법원 판결은 판사들이 한 사건에서 이전의 다른 판결들을 상기시킴으로써 그들의 결론을 뒷받침하기 때문에 또 다른 예를 제공한다.최종 예는 현재의 특허 청구와 관련된 이전 선행기술, 이전 특허를 참조해야 하는 특허에 의해 제공된다.지시된 반복 그래프의 특수 특성을 고려함으로써, 네트워크 분석을 사용하여 많은 연구에서 고려된 일반 그래프를 분석할 때 이용할 수 없는 기법으로 인용 네트워크를 분석할 수 있다.예를 들어, 타동성 감소는 다른 맥락에서 인용 네트워크를 생성하는 메커니즘의 분명한 차이를 강조하는 다른 애플리케이션에서 발견된 인용 분포에 대한 새로운 통찰력을 제공한다.[51]또 다른 기법은 인용 링크를 추적하고 주어진 인용 그래프에서 가장 중요한 인용 사슬을 제안하는 주경로 분석이다.

가격 모델은 인용 네트워크의 현실적인 모델이 되기에는 너무 단순하지만, 그것의 일부 특성에 대한 분석적 해결책을 허용하기에 충분히 간단하다.이들 중 상당수는 가격 모델의 간접적인 버전인 바라바시-알버트 모델에서 도출된 결과를 사용하여 찾을 수 있다.그러나 Price의 모델은 지시된 반복 그래프를 제공하기 때문에 지시된 반복 그래프에 고유한 속성의 분석적 계산을 찾을 때 유용한 모델이다.예를 들어 네트워크에 추가된 n번째 노드에서 네트워크의 첫 번째 노드에 이르기까지 가장 긴 경로의 길이는 () 로[52] 확장된다

데이터 압축

지시된 반복 그래프는 시퀀스 모음을 압축적으로 표현하기 위해 사용될 수도 있다.이러한 유형의 애플리케이션에서는 경로가 주어진 시퀀스를 구성하는 DAG를 찾는다.많은 시퀀스가 동일한 시퀀스를 공유하는 경우, 이러한 공유된 시퀀스는 DAG의 공유 부분으로 나타낼 수 있으며, 표현은 모든 시퀀스를 개별적으로 나열하는 데 필요한 공간보다 더 적은 공간을 사용할 수 있다.예를 들어, 지시된 반복 단어 그래프는 단일 출처와 문자나 기호로 표시된 가장자리를 가진 지시된 반복 그래프에 의해 형성된 컴퓨터 과학의 데이터 구조다. 이 그래프에서 출처에서 싱크까지의 경로는 영어 단어와 같은 문자열 집합을 나타낸다.[53]모든 시퀀스 집합은 시퀀스의 모든 접두사에 대한 트리 정점을 형성하고 이러한 정점 중 하나의 부모를 하나의 더 적은 원소로 시퀀스를 나타내도록 함으로써 트리의 경로로 나타낼 수 있다. 문자열 집합에 대해 이러한 방식으로 형성된 트리는 트리라고 불린다.지시된 반복 단어 그래프는 경로가 갈라지고 다시 결합할 수 있게 함으로써 삼위일체 위에 공간을 절약하여, 가능한 동일한 접미사를 가진 단어 집합을 하나의 나무 꼭지점으로 나타낼 수 있다.[54]

경로 패밀리를 나타내기 위해 DAG를 사용하는 것과 같은 생각이 이진 함수를 나타내기 위한 DAG 기반 데이터 구조인 이진 [55][56]결정 다이어그램에서 발생한다.이항 결정 다이어그램에서 각 비싱크 꼭지점은 이항 변수의 이름으로 표시되며, 각 싱크와 각 가장자리는 0 또는 1로 표시된다.변수에 대한 모든 진실 할당에 대한 함수 값은 단일 소스 정점에서 시작하여 각 비싱크 정점에서 해당 정점 변수의 값이 표시된 발신 에지를 따르는 경로를 추적하여 찾은 싱크에서의 값이다.지시된 반복 단어 그래프를 시도의 압축된 형태로 볼 수 있듯이, 이진 결정 도표는 남은 모든 결정의 결과에 동의할 때 경로가 다시 결합할 수 있도록 하여 공간을 절약하는 압축된 형태의 의사결정 나무로 볼 수 있다.[57]

참조

  1. ^ Thulasiraman, K.; Swamy, M. N. S. (1992), "5.7 Acyclic Directed Graphs", Graphs: Theory and Algorithms, John Wiley and Son, p. 118, ISBN 978-0-471-51356-8.
  2. ^ a b Bang-Jensen, Jørgen (2008), "2.1 Acyclic Digraphs", Digraphs: Theory, Algorithms and Applications, Springer Monographs in Mathematics (2nd ed.), Springer-Verlag, pp. 32–34, ISBN 978-1-84800-997-4.
  3. ^ Christofides, Nicos (1975), Graph theory: an algorithmic approach, Academic Press, pp. 170–174.
  4. ^ Mitrani, I. (1982), Simulation Techniques for Discrete Event Systems, Cambridge Computer Science Texts, vol. 14, Cambridge University Press, p. 27, ISBN 9780521282826.
  5. ^ Kozen, Dexter (1992), The Design and Analysis of Algorithms, Monographs in Computer Science, Springer, p. 9, ISBN 978-0-387-97687-7.
  6. ^ Banerjee, Utpal (1993), "Exercise 2(c)", Loop Transformations for Restructuring Compilers: The Foundations, Springer, p. 19, Bibcode:1993ltfr.book.....B, ISBN 978-0-7923-9318-4.
  7. ^ Bang-Jensen, Jørgen; Gutin, Gregory Z. (2008), "2.3 Transitive Digraphs, Transitive Closures and Reductions", Digraphs: Theory, Algorithms and Applications, Springer Monographs in Mathematics, Springer, pp. 36–39, ISBN 978-1-84800-998-1.
  8. ^ Jungnickel, Dieter (2012), Graphs, Networks and Algorithms, Algorithms and Computation in Mathematics, vol. 5, Springer, pp. 92–93, ISBN 978-3-642-32278-5.
  9. ^ Sedgewick, Robert; Wayne, Kevin (2011), "4,2,25 Unique topological ordering", Algorithms (4th ed.), Addison-Wesley, pp. 598–599, ISBN 978-0-13-276256-4.
  10. ^ Bender, Edward A.; Williamson, S. Gill (2005), "Example 26 (Linear extensions – topological sorts)", A Short Course in Discrete Mathematics, Dover Books on Computer Science, Courier Dover Publications, p. 142, ISBN 978-0-486-43946-4.
  11. ^ a b Robinson, R. W. (1973), "Counting labeled acyclic digraphs", in Harary, F. (ed.), New Directions in the Theory of Graphs, Academic Press, pp. 239–273. 또한 참조하십시오.
  12. ^ Weisstein, Eric W., "Weisstein's Conjecture", MathWorld
  13. ^ McKay, B. D.; Royle, G. F.; Wanless, I. M.; Oggier, F. E.; Sloane, N. J. A.; Wilf, H. (2004), "Acyclic digraphs and eigenvalues of (0,1)-matrices", Journal of Integer Sequences, 7: 33, arXiv:math/0310423, Bibcode:2004JIntS...7...33M, 제04조 3항.
  14. ^ Furnas, George W.; Zacks, Jeff (1994), "Multitrees: enriching and reusing hierarchical structure", Proc. SIGCHI conference on Human Factors in Computing Systems (CHI '94), pp. 330–336, doi:10.1145/191666.191778, ISBN 978-0897916509, S2CID 18710118.
  15. ^ Rebane, George; Pearl, Judea (1987), "The recovery of causal poly-trees from statistical data", in Proc. 3rd Annual Conference on Uncertainty in Artificial Intelligence (UAI 1987), Seattle, WA, USA, July 1987 (PDF), pp. 222–228.
  16. ^ a b Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001) [1990], Introduction to Algorithms (2nd ed.), MIT Press and McGraw-Hill, ISBN 0-262-03293-7 제22.4절, 위상학적 분류 549–552페이지.
  17. ^ a b Jungnickel(2012), 페이지 50–51.
  18. ^ 깊이-첫 번째 검색 기반 위상 정렬 알고리즘의 경우 이 유효성 검사는 위상 정렬 알고리즘 자체와 상호 저장될 수 있다(예: 참조).
  19. ^ Stanley, Richard P. (1973), "Acyclic orientations of graphs" (PDF), Discrete Mathematics, 5 (2): 171–178, doi:10.1016/0012-365X(73)90108-8.
  20. ^ Garey, Michael R.; Johnson, David S. (1979), Computers and Intractability: A Guide to the Theory of NP-Completeness, W. H. Freeman, ISBN 0-7167-1045-5, 문제 GT7 및 GT8, 페이지 191–192.
  21. ^ Harary, Frank; Norman, Robert Z.; Cartwright, Dorwin (1965), Structural Models: An Introduction to the Theory of Directed Graphs, John Wiley & Sons, p. 63.
  22. ^ 스키에나(2009), 페이지 495.
  23. ^ 스키에나(2009년), 페이지 496.
  24. ^ 방젠센 & 구틴(2008), 페이지 38.
  25. ^ Picard, Jean-Claude (1976), "Maximal closure of a graph and applications to combinatorial problems", Management Science, 22 (11): 1268–1272, doi:10.1287/mnsc.22.11.1268, MR 0403596.
  26. ^ Cormen 등, 2001, 섹션 24.2, 지시된 반복 그래프의 단일 소스 최단 경로 592–595페이지.
  27. ^ Cormen 등 2001, 섹션 24.1, Bellman-Ford 알고리즘 페이지 588–592 및 24.3, Dijkstra 알고리즘 페이지 595–601.
  28. ^ 코멘 외 연구진 2001, 966 페이지
  29. ^ 스키에나(2009), 페이지 469.
  30. ^ Al-Mutawa, H. A.; Dietrich, J.; Marsland, S.; McCartin, C. (2014), "On the shape of circular dependencies in Java programs", 23rd Australian Software Engineering Conference, IEEE, pp. 48–57, doi:10.1109/ASWEC.2014.15, ISBN 978-1-4799-3149-1, S2CID 17570052.
  31. ^ a b Gross, Jonathan L.; Yellen, Jay; Zhang, Ping (2013), Handbook of Graph Theory (2nd ed.), CRC Press, p. 1181, ISBN 978-1-4398-8018-0.
  32. ^ Srikant, Y. N.; Shankar, Priti (2007), The Compiler Design Handbook: Optimizations and Machine Code Generation (2nd ed.), CRC Press, pp. 19–39, ISBN 978-1-4200-4383-9.
  33. ^ Wang, John X. (2002), What Every Engineer Should Know About Decision Making Under Uncertainty, CRC Press, p. 160, ISBN 978-0-8247-4373-4.
  34. ^ Sapatnekar, Sachin (2004), Timing, Springer, p. 133, ISBN 978-1-4020-7671-8.
  35. ^ Dennis, Jack B. (1974), "First version of a data flow procedure language", Programming Symposium, Lecture Notes in Computer Science, vol. 19, pp. 362–376, doi:10.1007/3-540-06859-7_145, ISBN 978-3-540-06859-4.
  36. ^ Touati, Sid; de Dinechin, Benoit (2014), Advanced Backend Optimization, John Wiley & Sons, p. 123, ISBN 978-1-118-64894-0.
  37. ^ Garland, Jeff; Anthony, Richard (2003), Large-Scale Software Architecture: A Practical Guide using UML, John Wiley & Sons, p. 215, ISBN 9780470856383.
  38. ^ Gopnik, Alison; Schulz, Laura (2007), Causal Learning, Oxford University Press, p. 4, ISBN 978-0-19-803928-0.
  39. ^ Shmulevich, Ilya; Dougherty, Edward R. (2010), Probabilistic Boolean Networks: The Modeling and Control of Gene Regulatory Networks, Society for Industrial and Applied Mathematics, p. 58, ISBN 978-0-89871-692-4.
  40. ^ Cowell, Robert G.; Dawid, A. Philip; Lauritzen, Steffen L.; Spiegelhalter, David J. (1999), "3.2.1 Moralization", Probabilistic Networks and Expert Systems, Springer, pp. 31–33, ISBN 978-0-387-98767-5.
  41. ^ Dorf, Richard C. (1998), The Technology Management Handbook, CRC Press, p. 9-7, ISBN 978-0-8493-8577-3.
  42. ^ Boslaugh, Sarah (2008), Encyclopedia of Epidemiology, Volume 1, SAGE, p. 255, ISBN 978-1-4129-2816-8.
  43. ^ Pearl, Judea (1995), "Causal diagrams for empirical research", Biometrika, 82 (4): 669–709, doi:10.1093/biomet/82.4.669.
  44. ^ Kirkpatrick, Bonnie B. (April 2011), "Haplotypes versus genotypes on pedigrees", Algorithms for Molecular Biology, 6 (10): 10, doi:10.1186/1748-7188-6-10, PMC 3102622, PMID 21504603.
  45. ^ McGuffin, M. J.; Balakrishnan, R. (2005), "Interactive visualization of genealogical graphs" (PDF), IEEE Symposium on Information Visualization (INFOVIS 2005), pp. 16–23, doi:10.1109/INFVIS.2005.1532124, ISBN 978-0-7803-9464-3.
  46. ^ Bender, Michael A.; Pemmasani, Giridhar; Skiena, Steven; Sumazin, Pavel (2001), "Finding least common ancestors in directed acyclic graphs", Proceedings of the Twelfth Annual ACM-SIAM Symposium on Discrete Algorithms (SODA '01), Philadelphia, PA, USA: Society for Industrial and Applied Mathematics, pp. 845–854, ISBN 978-0-89871-490-6.
  47. ^ Bartlang, Udo (2010), Architecture and Methods for Flexible Content Management in Peer-to-Peer Systems, Springer, p. 59, Bibcode:2010aamf.book.....B, ISBN 978-3-8348-9645-2.
  48. ^ Pach, János; Sharir, Micha, Combinatorial Geometry and Its Algorithmic Applications: The Alcalá Lectures, Mathematical surveys and monographs, vol. 152, American Mathematical Society, pp. 93–94, ISBN 978-0-8218-7533-9.
  49. ^ Price, Derek J. de Solla (July 30, 1965), "Networks of Scientific Papers" (PDF), Science, 149 (3683): 510–515, Bibcode:1965Sci...149..510D, doi:10.1126/science.149.3683.510, PMID 14325149.
  50. ^ Price, Derek J. de Solla (1976), "A general theory of bibliometric and other cumulative advantage processes", Journal of the American Society for Information Science, 27 (5): 292–306, doi:10.1002/asi.4630270505.
  51. ^ Clough, James R.; Gollings, Jamie; Loach, Tamar V.; Evans, Tim S. (2015), "Transitive reduction of citation networks", Journal of Complex Networks, 3 (2): 189–203, arXiv:1310.8224, doi:10.1093/comnet/cnu039, S2CID 10228152.
  52. ^ Evans, T.S.; Calmon, L.; Vasiliauskaite, V. (2020), "The Longest Path in the Price Model", Scientific Reports, 10 (1): 10503, arXiv:1903.03667, Bibcode:2020NatSR..1010503E, doi:10.1038/s41598-020-67421-8, PMC 7324613, PMID 32601403
  53. ^ Crochemore, Maxime; Vérin, Renaud (1997), "Direct construction of compact directed acyclic word graphs", Combinatorial Pattern Matching, Lecture Notes in Computer Science, vol. 1264, Springer, pp. 116–129, CiteSeerX 10.1.1.53.6273, doi:10.1007/3-540-63220-4_55, ISBN 978-3-540-63220-7.
  54. ^ Lothaire, M. (2005), Applied Combinatorics on Words, Encyclopedia of Mathematics and its Applications, vol. 105, Cambridge University Press, p. 18, ISBN 9780521848022.
  55. ^ Lee, C. Y. (1959), "Representation of switching circuits by binary-decision programs", Bell System Technical Journal, 38 (4): 985–999, doi:10.1002/j.1538-7305.1959.tb01585.x.
  56. ^ Akers, Sheldon B. (1978), "Binary decision diagrams", IEEE Transactions on Computers, C-27 (6): 509–516, doi:10.1109/TC.1978.1675141, S2CID 21028055.
  57. ^ Friedman, S. J.; Supowit, K. J. (1987), "Finding the optimal variable ordering for binary decision diagrams", Proc. 24th ACM/IEEE Design Automation Conference (DAC '87), New York, NY, USA: ACM, pp. 348–356, doi:10.1145/37888.37941, ISBN 978-0-8186-0781-3, S2CID 14796451.

외부 링크