피드백 호 세트
Feedback arc set그래프 이론과 그래프 알고리즘에서 지시된 그래프에 설정된 피드백 호 집합 또는 피드백 에지는 그래프에서 모든 사이클 중 적어도 하나의 에지를 포함하는 그래프 에지의 부분 집합이다.그래프에서 이러한 가장자리를 제거하면 모든 사이클이 중단되어 주어진 그래프의 반복 하위 그래프인 방향의 반복 그래프가 생성된다.가능한 가장자리가 가장 적은 피드백 호 집합은 최소 피드백 호 집합이고 그 제거는 최대 반복 하위 그래프를 남긴다; 이러한 최적화 문제의 가중 버전도 사용된다.피드백 호 집합이 최소인 경우, 즉 그 집합에서 어떤 가장자리를 제거하면 피드백 호 집합이 아닌 부분집합이 생성된다는 것을 의미하며, 추가 특성이 있다: 가장자리를 모두 제거하기보다는 반대로 하면 지시된 AC 순환 그래프가 생성된다.
피드백 아크 세트에는 회로 분석, 화학공학, 교착해결, 순위투표, 스포츠 이벤트 랭킹 경쟁자, 수학심리학, 윤리학, 그래프 그리기 등에 응용이 있다.최소 피드백 호 집합과 최대 반복 하위 그래프를 찾는 것은 NP-hard이며, 지수 시간 또는 고정 매개변수 추적 가능 시간에서 정확히 해결할 수 있다.다항식 시간에서, 최소 피드백 호 세트는 다항 근사비 내에서 근사할 수 있으며, 최대 반복 하위 그래프는 상수 인자 내에서 근사할 수 있다.둘 다 어떤 일정한 요소보다 근사하게 접근하기 힘든데, 이것은 독특한 게임 추측 하에서 강화될 수 있는 유사성 결과물이다.토너먼트 그래프의 경우 최소 피드백 호 집합은 더 정확하게 추정할 수 있으며 평면 그래프의 경우 두 문제 모두 다항식 시간 내에 정확하게 해결할 수 있다.
밀접하게 관련된 문제인 피드백 꼭지점 집합은 방향 또는 방향 지정되지 않은 그래프의 모든 사이클에서 최소한 하나의 꼭지점을 포함하는 정점 집합이다.비방향 그래프에서 스패닝 트리는 가장 큰 반복 하위 그래프이며, 스패닝 트리를 형성할 때 제거된 가장자리 수는 회로 등급이다.
적용들

각 정점 쌍 사이에 하나의 가장자리가 있는 방향 그래프인 토너먼트 그래프에 설정된 피드백 호를 찾으면 순위나 순서와 관련된 몇 가지 문제를 해결할 수 있다.피드백 아크 세트의 가장자리를 반전시키면 방향의 아세클릭 그래프가 생성되며, 이 그래프는 고유한 위상학적 순서를 원하는 랭킹으로 사용할 수 있다.이 방법의 적용은 다음과 같다.
- 라운드 로빈 플레이가 있는 스포츠 경기에서는 패자부터 각 경기의 승자까지 우열을 가려서 각 경기의 결과를 기록할 수 있다.결과 그래프에서 최소 피드백 호를 찾고, 가장자리를 반전시키며, 위상학적 순서를 지정하면 모든 참가자에게 랭킹이 주어진다.랭킹을 선택하는 여러 가지 방법 중 하위권 경쟁자가 상위권 경쟁자를 이기는 게임인 총 업셋 수를 최소화한다.[2][3][4]많은 스포츠는 각 게임에 대해 부여된 점수를 기반으로 하는 단체 토너먼트 랭킹 시스템에 더 간단한 방법을 사용한다.[5] 이러한 방법은 최소 업셋 랭킹에 대해 일정한 근사를 제공할 수 있다.[6]
- 영장류학에서 그리고 더 일반적으로 윤리학에서 지배 계층 구조는 종종 관찰된 지배 행동에서 가장 적은 역순으로, 최소 피드백 호 집합 문제의 또 다른 형태인 순서를 검색함으로써 결정된다.[7][8][9]
- 수학 심리학에서, 모든 물체 쌍들 간의 쌍별 비교에 기초하여, 그들의 선호도나 크기에 대한 인식과 같은 주어진 기준에 따라 물체 집합에 대한 피험자의 순위를 결정하는 것이 흥미롭다.토너먼트 그래프에서 설정된 최소 피드백 호는 가능한 한 쌍의 결과물에 동의하지 않는 순위를 제공한다.[2][10]또는 이러한 비교로 각 쌍 순서에 대한 독립 확률이 발생하는 경우, 이러한 확률을 로그 우도로 변환하고 결과 토너먼트에서 설정된 최소 가중치 피드백 호를 찾아 전체 랭킹의 최대우도 추정치를 얻을 수 있다.[2][3]
- 동일한 최대 우도 순서가 요소들 간의 쌍방향 비교를 제공하는 데이터를 사용할 수 있는 경우, 요소를 선형 순서로 배열하는 통계 및 탐색 데이터 분석에 사용될 수 있다.[3][11][12]
- 순위투표에서 케메니-.젊은 방법은 후보 쌍에 비해 반대 순서를 선호하는 유권자 수의 합계를 최소화하는 주문을 추구하는 것으로 설명할 수 있다.[13]이는 정점이 후보를 나타내고, 가장자리가 각 정면승부의 승자를 나타내며, 각 가장자리 비용은 앞머리 패자에게 더 높은 순위를 줌으로써 불행해질 유권자 수를 나타내는 최소 무게 피드백 아크 세트 문제로 공식화하여 해결할 수 있다.[14]
피드백 아크 세트의 또 다른 초기 적용은 순차 논리 회로의 설계와 관련이 있는데, 이 회로에서는 신호가 항상 입력에서 출력으로 진행되지 않고 회로를 통해 사이클로 전파될 수 있다.그러한 회로에서 최소 피드백 아크 세트는 신호가 정보의 손실 없이 전파될 수 있도록 하기 위해 증폭이 필요한 지점의 수를 특징짓는다.[15]비동기 구성요소로 만들어진 동기 회로에서는 클록으로 표시된 게이트를 피드백 아크 세트의 가장자리에 배치하여 동기화를 달성할 수 있다.[16]또한 피드백 아크 세트의 회로를 절단하면 나머지 회로가 결합 논리로 감소하여 분석이 단순화되며, 피드백 아크 세트의 크기는 컷 통과 회로의 동작을 이해하기 위해 얼마나 많은 추가 분석이 필요한지 제어한다.[15]마찬가지로, 화학공학에서 프로세스 흐름 시팅에서 피드백 아크 세트의 프로세스 흐름도의 가장자리를 파괴하고, 그 가장자리 값에 대한 모든 가능성을 추측하거나 시도하면 나머지 공정은 그것의 반복성 때문에 체계적인 방법으로 분석될 수 있다.이 어플리케이션에서는, 이런 식으로 가장자리를 꺾는 것을 「테어링」[17]이라고 한다.
레이어드 그래프 도면에서 주어진 방향 그래프의 정점은 순서가 정해진 하위 집합(도면의 층)의 순서에 따라 분할되며, 각 부분집합은 이 도면층의 수평선을 따라 배치되며, 가장자리는 이들 층 사이에 위아래로 확장된다.이러한 유형의 도면에서 도면의 도달 가능성 관계가 보다 시각적으로 뚜렷해지려면 대부분의 또는 모든 가장자리가 위아래로 혼합되지 않고 아래쪽으로 일관되게 방향을 잡는 것이 바람직하다.이는 최소 또는 최소 피드백 호 세트를 찾아 해당 집합의 가장자리를 반전시킨 다음 결과의 반복 그래프의 위상학적 순서와 일치하는 방식으로 분할을 레이어별로 선택함으로써 달성된다.[18][19]또한 연속적인 레이어 쌍 내 정점의 순서인 레이어드 그래프 도면의 다른 하위 문제에 피드백 아크 세트가 사용되었다.[20]
운영체제의 교착해결에서, 교착상태를 타개하기 위해 최소한의 의존성을 제거하는 문제는 최소 피드백 호 집합을 찾는 것의 하나로 모델링될 수 있다.[21][22]그러나, 이 세트를 찾기 위한 계산상의 어려움,[22] 그리고 운영 체제 컴포넌트 내의 속도의 필요성 때문에, 이 어플리케이션에서는 정확한 알고리즘보다는 휴리스틱스가 자주 사용된다.
알고리즘
등가성
최소 피드백 호 집합과 최대 반복 하위 그래프는 정확한 최적화를 위해 동등하다. 하나는 다른 하나의 보완 집합이기 때문이다.그러나 매개변수화된 복잡성과 근사치의 경우, 이러한 종류의 알고리즘에 사용되는 분석은 입력 그래프의 크기뿐만 아니라 솔루션의 크기에 따라 달라지며, 최소 피드백 호 집합과 최대 반복 하위 그래프의 크기가 서로 다르기 때문에 서로 다르다.[23]
주어진 그래프 의 피드백 호 집합은 의 방향선 그래프의 피드백 꼭지점 집합과 동일하다 여기서 피드백 정점 집합은 모든 주기가 제거되는 그래프의 정점 집합과 유사하게 정의된다.방향 그래프 의 선 그래프는 G의 각 에지에 대한 정점 및 의 각 두 에지 경로에 대한 에지를 가지고 있다 다른 방향에서는 주어진 그래프 의 최소 피드백 정점 세트를 솔루션에서 최소 피드백 호로 얻을 수 있다. 의 모든 꼭지점을 두 개의 꼭지점으로 분할하여 얻은 그래프에서 문제를 설정하십시오.이러한 변환을 통해 피드백 호 집합과 피드백 정점 집합에 대한 정확한 알고리즘을 서로 변환할 수 있으며, 복잡도 범위를 적절하게 변환할 수 있다.그러나 이 변환은 최대 반복 하위 그래프 문제에 대한 근사 품질을 보존하지 않는다.[21][24]
피드백 아크 세트 문제에 대한 정확한 해결책과 대략적인 해결책 모두에서, 주어진 그래프의 각각의 강하게 연결된 구성요소를 개별적으로 해결하는 것으로 충분하며, 이러한 강하게 연결된 구성요소를 관절 정점으로부터 분리함으로써 두 개의 결합 구성요소로 더 멀리 떨어뜨리는 것으로 충분하다.이러한 하위 문제들 중 하나 내에서 해결책의 선택은 다른 문제에는 영향을 미치지 않으며, 이러한 구성 요소들 중 어느 하나에도 나타나지 않는 가장자리는 피드백 아크 세트에 포함하는데 유용하지 않다.[25]두 개의 정점을 제거하여 이들 구성 요소 중 하나를 두 개의 분리된 하위 그래프로 분리할 수 있는 경우, 문제가 강하게 연결된 구성 요소의 트리코넥트 구성 요소에서 파생된 하위 문제로 분할될 수 있도록 더 복잡한 분해 작업이 적용된다.[26]
정확한
최소 피드백 호 집합을 찾는 한 가지 방법은 가능한 한 적은 수의 가장자리가 순서의 이후 정점에서 이전 정점으로 지시되도록 정점의 순서를 검색하는 것이다.[27] -vertex 그래프의 모든 순열은 !) O 시간이 걸리지만, Hold-Karp 알고리즘에 기초한 동적 프로그래밍 방법은 기하급수적인 공간의 양을 사용하여 O 에서 최적의 순열을 찾을 수 있다[28][29]정점의 모든 파티션을 두 개의 동일한 서브셋과 각 서브셋 내의 재귀로 테스트하는 분할 및 변환 알고리즘은 다항식 공간을 O(/ n O 시간 내에 문제를 해결할 수 있다.[29]
매개변수화된 복잡도에서 알고리즘에 대한 시간은 입력 그래프의 크기뿐만 아니라 그래프의 별도 매개변수 측면에서도 측정된다.특히, 최소 피드백 아크 세트 문제의 경우, 이른바 자연 매개변수는 최소 피드백 아크 세트의 크기를 의미한다. 정점이 있는 그래프에서 자연 k{\ 과 같은 정점 집합 문제로 변환하고 변수화된 피드백 정점 se를 적용하여 피드백 호 집합 문제를 O( 에서 해결할 수 있다t 알고리즘.이 알고리즘에서 의 지수가 과와) 독립된 상수 {\이기 때문에 이 알고리즘은 고정 매개변수 추적 가능하다고 한다[30]
자연 매개변수 이외의 다른 매개변수도 연구되었다.동적 프로그래밍을 사용하는 고정 매개변수 추적 가능한 알고리즘은 시간 2 m m O에서 최소 피드백 호 세트를 찾을 수 있으며 여기서 은 기본 비방향 그래프의 회로 순위다.회로 등급은 피드백 호 집합의 비방향 아날로그로, 이를 스패닝 트리로 줄이기 위해 그래프에서 제거해야 하는 최소 에지 수입니다. 최소 피드백 호 집합보다 계산하기가 훨씬 쉽다.[24] 너비t {\그래프의 경우, 그래프의 트리 분해에 대한 동적 프로그래밍은 그래프 크기에서 시간 다항식으로 설정된 최소 피드백 호를 수 있고 O( t) {\ Olog t에서 지수적으로 찾을 수 있다 지수 시간 가설에서 t {\에 더 나은 의존은 없다가능한[31]
연구자들은 피드백 아크 세트의 크기를 최소화하는 대신 정점에서 제거된 최대 가장자리 수를 최소화하는 방법을 연구했다.이 문제의 변형은 선형 시간 안에 해결될 수 있다.[32]모든 최소 피드백 아크 세트는 집합당 다항식 지연이 있는 알고리즘에 의해 나열될 수 있다.[33]
근사치
피드백 아크 세트에 대해 가장 잘 알려진 다항식 시간 근사 알고리즘에는 비정수 O n ){\O(\log n\ n)}가 있다즉, 발견된 피드백 호 집합의 크기가 최대 이 인자가 최적 인자보다 크다는 것을 의미한다.[21]피드백 호 집합에 일정한 비율 근사 알고리즘이 있는지 또는 일정하지 않은 비율이 필요한지 여부를 결정하는 것은 개방적인 문제로 남아 있다.[34]
최대 Acyclic 하위 그래프 문제는 1 근사 비율을 달성하는 쉬운 근사 알고리즘을 가지고 있다
- 정점의 임의 순서 수정
- 가장자리를 두 개의 악순환 하위 그래프로 분할한다. 하나는 순서와 일관되게 지시된 가장자리로 구성되고 다른 하나는 순서와 정반대 방향으로 지시된 가장자리로 구성된다.
- 두 개의 하위 그래프 중 더 큰 것을 반환하십시오.
이것은 탐욕스러운 알고리즘을 사용하여 순서를 선택함으로써 개선될 수 있다.이 알고리즘은 들어오는 에지와 나가는 에지 수가 가능한 멀리 떨어져 있는 정점을 찾아 삭제하고, 남은 그래프를 재귀적으로 오더한 다음, 삭제된 정점을 결과 순서의 한쪽 끝에 배치한다.m{m\displaystyle}가장자리와 엔{n\displaystyle}vertices과 그래프의 경우 이 m/2+, 선형 시간에,(n/m)12+Ω에 대한 근사치 비율{\displaystyle{\tfrac{1}{2}}+\Omega(n/m)을 주는}또 다른 더욱 복잡한, 가난한 .[35] 원자가 비고리형인 부분 그래프 n/6{\displaystyle m/2+n/6}가장자리를 생산한다.lynomial time approximation algorithm applies to graphs with maximum degree , and finds an acyclic subgraph with edges, giving an approximation ratio of the form [36][37]= 3 일 때 근사비 / 8를 달성할 수 있다.[38]
입력 제한
지시된 평면 그래프에서 피드백 아크 세트 문제는 결과 그래프를 강하게 연결하기 위해 가장자리 집합을 수축하는 문제와 이중적이다.[39]이 이중 문제는 다항식으로 해결할 수 있으며,[40] 따라서 평면 최소 피드백 아크 세트 문제도 역시 해결 가능하다.[41][40]그것은 시대를 통틀어 O에서 .[42]문제에 대한 가중 버전 시대를 통틀어 O에서(n3)또는 가장에 있을 경우 몸무게는 양의 정수 시간에 O(n5/2로그 nN){\와 같이 많은 N{N\displaystyle},{O(n^{3})\displaystyle},[39]해결될 수 있(n5/2로그 n){O(n^{5/2}n\log)\displaystyle}해결될 수 있다.디스플레이 O[42].이러한 평면 알고리즘은 그래프 마이너로서 효용 그래프 3, 가 없는 그래프까지 확장할 수 있으며, 이러한 그래프의 트리코넥트된 성분이 평면형 또는 경계형 크기라는 사실을 사용할 수 있다.[26]평면 그래프는 또한 피드백 호 집합과 관련된 특정 폴리토프의 통합성에 의해 정의되는 약하게 순환되는 디그래프라고 불리는 지시된 그래프의 종류와는 다른 방식으로 일반화되었다.이러한 의미에서 모든 평면 방향 그래프는 약하게 악순환하며, 피드백 아크 세트 문제는 모든 약하게 악순환 디그래프에 대해 다항식으로 해결할 수 있다.[43]
환원 가능한 흐름 그래프는 다항식 시간에 피드백 호 세트 문제를 해결할 수 있는 다른 종류의 지시된 그래프다.이 그래프들은 많은 프로그래밍 언어의 구조화된 프로그램에서 제어의 흐름을 설명한다.구조화된 프로그램은 종종 평면 방향 흐름 그래프를 생성하지만, 축소성의 정의는 그래프를 평면적으로 만들 필요가 없다.[44]
최소 피드백 아크 세트 문제가 토너먼트로 제한될 경우, 다항식 시간 근사 체계가 있어 문제의 가중 버전에 일반화된다.[45]토너먼트에서 가중 피드백 호 집합에 대한 하위 성능 매개변수 알고리즘도 알려져 있다.[14]밀도 그래프의 최대 반복 하위 그래프 문제도 다항식 시간 근사도를 가지고 있다.문제의 선형 프로그래밍 완화에 무작위 반올림을 적용하고, 확장기 그래프의 워크를 이용해 결과 알고리즘을 세분화하는 것이 주요 아이디어다.[34][46]
경도
NP-강경성
최소 피드백 호 집합에 NP-완전성 이론을 적용하기 위해서는 최적화 문제(모든 사이클을 깨기 위해 몇 개의 에지를 제거할 수 있는지)에서 예스 또는 노스톱으로 동등한 의사결정 버전으로 문제를 수정할 필요가 있다( 엣지를 제거할 수 있는가).따라서 피드백 아크 세트 문제의 결정 버전은 방향 그래프와 숫자 를 모두 입력하는 것으로 간주된다 k 가장자리를 제거하여 모든 사이클을 중단시킬 수 있는지, 아니면 최소한 ( )- - 를 가진 반복 하위 그래프가 있는지 동등하게 묻는다. 가장자리.이 문제는 NP-완전성으로, NP-완전성으로, 이 문제나 최적화 문제 중 어느 것도 다항 시간 알고리즘을 가질 것으로 예상되지 않음을 시사한다.그것은 리차드 M. Karp의 원래 21개의 NP 완성 문제들 중 하나였다; 그것의 NP 완성도는 Karp와 유진 Lawler에 의해 정점 커버 문제에 대한 입력들이 피드백 아크 세트 결정 문제와 동등한 입력으로 변환될 수 있다는 것을 보여줌으로써 Karp와 Eugene Lawler에 의해 증명되었다.[47][48]
일부 NP완전성 문제들은 그들의 입력이 특별한 경우에 제한될 때 더 쉬워질 수 있다.그러나 피드백 아크 세트 문제의 가장 중요한 특별한 경우, 토너먼트의 경우, 문제는 NP-완전 상태로 남아 있다.[49][50]
근사치
복잡도 등급 APX는 일정한 근사 비율을 달성하는 다항 시간 근사 알고리즘을 가진 최적화 문제로 구성된다.그러한 근사치는 피드백 아크 세트 문제에 대해 알려져 있지 않지만, 문제는 APX-hard인 것으로 알려져 있다. 즉, APX의 다른 모든 문제에 대해 유사한 정확한 근사치를 얻기 위해 그에 대한 정확한 근사치를 사용할 수 있다.경도 입증 결과 P = NP가 아닌 한, 1.3606보다 높은 다항 시간 근사비를 가지지 않는다.이는 정점 커버로 알려진 근사 경도에 대한 동일한 임계값이며, 교정에서는 정점 커버에서 피드백 아크 세트로 Karp-Lawler 감소를 사용하여 근사치의 품질을 보존한다.[34][51][52][53]다른 감소에 의해, 최대 반복 서브그래프 문제는 또한 APX-hard이고 NP-hard는 최적 인자의 65/66 이내에 근사하게 된다.[38]
이러한 문제의 근사치 경도는 또한 계산 복잡성 이론에서는 표준이지만 P n NP보다 강한 입증되지 않은 계산 경도 가정 하에서 연구되었다. 만일 독특한 게임 추측이 사실이라면, 최소 피드백 아크 세트 문제는 다항 시간 내에 일정한 사실 내에서 근사하기 어렵다.만약 지수 시간 가설은 사실이다 그런 다음 모든 ε>0 아니면 최대 피드백 아크 집합 문제}, 모든 ε 을을 위해 12+ε{\displaystyle{\tfrac{1}{2}}+\varepsilon의 요인 최대에 근접하게 하는 것뿐, 근사 알고리즘에 대한 다항 시간 외에 0{\displaystyle \varepsilon>0}.[54], 어렵다. {\displaysty 최소 피드백 아크 세트에는 하위존재 시간 O -에서 계산될 수 있는 6 - {\{ 내에 근사가 없다[55]
이론
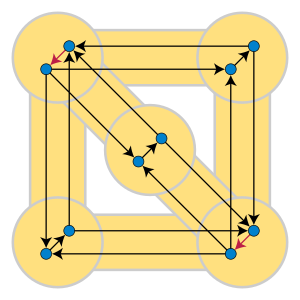
평면 지시 그래프에서 피드백 아크 세트 문제는 최소-최대 정리를 준수한다. 피드백 아크 세트의 최소 크기는 그래프에서 찾을 수 있는 최대 에지 분리 지시 사이클 수와 같다.[41][56]일부 다른 그래프에서는 그렇지 않다. 예를 들어 첫 번째 그림은 비 평면 그래프 , 의 지시된 버전을 보여주는데, 이 그래프에서는 피드백 호 세트의 최소 크기가 2인 반면 최대 에지 분리 지시 주기의 수는 1개에 불과하다.
모든 토너먼트 그래프에는 해밀턴의 경로가 있으며, 해밀턴의 경로는 최소 피드백 아크 세트로 1대1로 대응하여 해당 경로에서 분리된다.피드백 아크 세트의 해밀턴 경로는 호를 반전시켜 결과의 ACL 토너먼트의 위상학적 순서를 찾음으로써 찾을 수 있다.연속된 순서의 모든 쌍은 피드백 호 세트에서 분리되어야 한다. 그렇지 않으면 그 쌍을 반전시킴으로써 더 작은 피드백 호 세트를 발견할 수 있기 때문이다.따라서, 이 순서는 모든 정점을 커버하는 원래의 토너먼트의 호를 통과하는 길을 제공한다.반대로, 어떤 해밀턴 경로에서, 경로의 나중의 꼭지점과 이전의 꼭지점을 연결하는 가장자리 집합은 피드백 호 집합을 형성한다.각각의 가장자리는 다른 모든 사이클과 분리된 해밀턴 경로 가장자리의 사이클에 속하기 때문에 최소값이다.[57]토너먼트에서 최소 피드백 호 세트와 최대 반복 하위 그래프가 둘 다 가장자리 절반에 가까운 경우일 수 있다.좀 더 정밀하게, 모든 토너먼트 그래프, 그리고 몇몇 대회 O(n3/2){\displaystyle{\tbinom{n}{2}}(n^{3/2})}거의 모든 대회 들어, th.[58]− 크기(n2)/2이 필요한 규모의 피드백 아크 세트(n2)/2− Ω(n3/2){\displaystyle{\tbinom{n}{2}}/2-\Omega(n^{3/2})}이 있다.esize is at least .[59] Every directed acyclic graph can be embedded as a subgraph of a larger tournament graph, in such a way that is the unique minimum feedback arc set of the tournament.이 의 크기는D D}의 "역전 번호"로 정의되었으며, 수가 동일한 방향의 순환 그래프 중에서 D {\displaystyle D가 () 토너먼트일 때 가장 크다.[60][61]
방향 그래프는 강하게 연결될 때마다 오일러 투어가 있고 각 정점에는 동일한 수의 들어오고 나가는 가장자리가 있다.이러한 그래프의 경우, 에지와 정점을 가진 최소 피드백 호 세트의 크기는 항상 최소 2+ 이 구속이 엄격한 오일러식 지시 그래프가 무한히 많다.[62]방향 그래프가 정점당 가장자리가 최대 3개인 정점을 갖는 경우, 최대 / 3 n의 가장자리로 이루어진 피드백 호 집합을 가지며, 일부 그래프에는 이 수가 필요하다.지시된 그래프가 정점당 최대 4개의 가장자리가 m{\ 에지를 가진 경우, m{\ 에지의 피드백 호 집합이 있으며, 일부 그래프에는 이 수가 필요하다.[63]
참조
- ^ "Main draw – Men", Rio 2016, Fédération Internationale de Volleyball, archived from the original on 2016-12-23, retrieved 2021-11-14
- ^ a b c Hubert, Lawrence (1976), "Seriation using asymmetric proximity measures", British Journal of Mathematical and Statistical Psychology, 29 (1): 32–52, doi:10.1111/j.2044-8317.1976.tb00701.x, MR 0429180
- ^ a b c Remage, Russell Jr.; Thompson, W. A. Jr. (1966), "Maximum-likelihood paired comparison rankings", Biometrika, 53 (1–2): 143–149, doi:10.1093/biomet/53.1-2.143, JSTOR 2334060, MR 0196854, PMID 5964054
- ^ Goddard, Stephen T. (1983), "Ranking in tournaments and group decisionmaking", Management Science, 29 (12): 1384–1392, doi:10.1287/mnsc.29.12.1384, MR 0809110; 최소 위반 순위를 찾기 위해 Goddard가 제안한 알고리즘이 잘못되었다는 점에 유의하십시오.
- ^ Vaziri, Baback; Dabadghao, Shaunak; Yih, Yuehwern; Morin, Thomas L. (January 2018), "Properties of sports ranking methods", Journal of the Operational Research Society, 69 (5): 776–787, doi:10.1057/s41274-017-0266-8, S2CID 51887586
- ^ Coppersmith, Don; Fleischer, Lisa K.; Rurda, Atri (2010), "Ordering by weighted number of wins gives a good ranking for weighted tournaments", ACM Transactions on Algorithms, 6 (3): A55:1–A55:13, doi:10.1145/1798596.1798608, MR 2682624, S2CID 18416
- ^ Seyfarth, Robert M. (November 1976), "Social relationships among adult female baboons", Animal Behaviour, 24 (4): 917–938, doi:10.1016/s0003-3472(76)80022-x, S2CID 54284406
- ^ Estep, D.Q.; Crowell-Davis, S.L.; Earl-Costello, S.-A.; Beatey, S.A. (January 1993), "Changes in the social behaviour of drafthorse (Equus caballus) mares coincident with foaling", Applied Animal Behaviour Science, 35 (3): 199–213, doi:10.1016/0168-1591(93)90137-e
- ^ Eickwort, George C. (April 2019), "Dominance in a cockroach (Nauphoeta)", Insect Behavior, CRC Press, pp. 120–126, doi:10.1201/9780429049262-18, S2CID 203898549
- ^ Slater, Patrick (1961), "Inconsistencies in a schedule of paired comparisons", Biometrika, 48 (3–4): 303–312, doi:10.1093/biomet/48.3-4.303, JSTOR 2332752
- ^ Brunk, H. D. (1960), "Mathematical models for ranking from paired comparisons", Journal of the American Statistical Association, 55 (291): 503–520, doi:10.2307/2281911, hdl:2027/mdp.39015095254010, JSTOR 2281911, MR 0115242
- ^ Thompson, W. A., Jr.; Remage, Russell, Jr. (1964), "Rankings from paired comparisons", Annals of Mathematical Statistics, 35 (2): 739–747, doi:10.1214/aoms/1177703572, JSTOR 2238526, MR 0161419
- ^ Kemeny, John G. (Fall 1959), "Mathematics without numbers", Daedalus, 88 (4): 577–591, JSTOR 20026529
- ^ a b Karpinski, Marek; Schudy, Warren (2010), "Faster algorithms for feedback arc set tournament, Kemeny rank aggregation and betweenness tournament", in Cheong, Otfried; Chwa, Kyung-Yong; Park, Kunsoo (eds.), Algorithms and Computation - 21st International Symposium, ISAAC 2010, Jeju Island, Korea, December 15-17, 2010, Proceedings, Part I, Lecture Notes in Computer Science, vol. 6506, Springer, pp. 3–14, arXiv:1006.4396, doi:10.1007/978-3-642-17517-6_3, S2CID 16512997
- ^ a b Unger, Stephen H. (April 26, 1957), A study of asynchronous logical feedback networks, Technical reports, vol. 320, Massachusetts Institute of Technology, Research Laboratory of Electronics, hdl:1721.1/4763
- ^ Feehrer, John R.; Jordan, Harry F. (December 1995), "Placement of clock gates in time-of-flight optoelectronic circuits", Applied Optics, 34 (35): 8125–8136, Bibcode:1995ApOpt..34.8125F, doi:10.1364/ao.34.008125, PMID 21068927
- ^ Rosen, Edward M.; Henley, Ernest J. (Summer 1968), "The New Stoichiometry", Chemical Engineering Education, 2 (3): 120–125, archived from the original on 2021-08-02, retrieved 2021-08-02
- ^ Di Battista, Giuseppe; Eades, Peter; Tamassia, Roberto; Tollis, Ioannis G. (1998), "Layered Drawings of Digraphs", Graph Drawing: Algorithms for the Visualization of Graphs, Prentice Hall, pp. 265–302, ISBN 9780133016154
- ^ Bastert, Oliver; Matuszewski, Christian (2001), "Layered drawings of digraphs", in Kaufmann, Michael; Wagner, Dorothea (eds.), Drawing Graphs: Methods and Models, Lecture Notes in Computer Science, vol. 2025, Springer-Verlag, pp. 87–120, doi:10.1007/3-540-44969-8_5
- ^ Demetrescu, Camil; Finocchi, Irene (2001), "Break the "right" cycles and get the "best" drawing", ACM Journal of Experimental Algorithmics, 6: 171–182, MR 2027115
- ^ a b c Even, G.; Naor, J.; Schieber, B.; Sudan, M. (1998), "Approximating minimum feedback sets and multicuts in directed graphs", Algorithmica, 20 (2): 151–174, doi:10.1007/PL00009191, MR 1484534, S2CID 2437790
- ^ a b Minoura, Toshimi (1982), "Deadlock avoidance revisited", Journal of the ACM, 29 (4): 1023–1048, doi:10.1145/322344.322351, MR 0674256, S2CID 5284738
- ^ Mishra, Sounaka; Sikdar, Kripasindhu (2004), "On approximability of linear ordering and related NP-optimization problems on graphs", Discrete Applied Mathematics, 136 (2–3): 249–269, doi:10.1016/S0166-218X(03)00444-X, MR 2045215
- ^ a b Hecht, Michael (2017), "Exact localisations of feedback sets", Theory of Computing Systems, 62 (5): 1048–1084, arXiv:1702.07612, doi:10.1007/s00224-017-9777-6, S2CID 18394348
- ^ Park, S.; Akers, S.B. (1992), "An efficient method for finding a minimal feedback arc set in directed graphs", Proceedings of the 1992 IEEE International Symposium on Circuits and Systems (ISCAS '92), vol. 4, pp. 1863–1866, doi:10.1109/iscas.1992.230449, S2CID 122603659
- ^ a b Nutov, Zeev; Penn, Michal (2000), "On integrality, stability and composition of dicycle packings and covers", Journal of Combinatorial Optimization, 4 (2): 235–251, doi:10.1023/A:1009802905533, MR 1772828, S2CID 207632524
- ^ Younger, D. (1963), "Minimum feedback arc sets for a directed graph", IEEE Transactions on Circuit Theory, 10 (2): 238–245, doi:10.1109/tct.1963.1082116
- ^ Lawler, E. (1964), "A comment on minimum feedback arc sets", IEEE Transactions on Circuit Theory, 11 (2): 296–297, doi:10.1109/tct.1964.1082291
- ^ a b Bodlaender, Hans L.; Fomin, Fedor V.; Koster, Arie M. C. A.; Kratsch, Dieter; Thilikos, Dimitrios M. (2012), "A note on exact algorithms for vertex ordering problems on graphs", Theory of Computing Systems, 50 (3): 420–432, doi:10.1007/s00224-011-9312-0, hdl:1956/4556, MR 2885638, S2CID 9967521
- ^ Chen, Jianer; Liu, Yang; Lu, Songjian; O'Sullivan, Barry; Razgon, Igor (2008), "A fixed-parameter algorithm for the directed feedback vertex set problem", Journal of the ACM, 55 (5): 1–19, doi:10.1145/1411509.1411511, S2CID 1547510
- ^ Bonamy, Marthe; Kowalik, Lukasz; Nederlof, Jesper; Pilipczuk, Michal; Socala, Arkadiusz; Wrochna, Marcin (2018), "On directed feedback vertex set parameterized by treewidth", in Brandstädt, Andreas; Köhler, Ekkehard; Meer, Klaus (eds.), Graph-Theoretic Concepts in Computer Science - 44th International Workshop, WG 2018, Cottbus, Germany, June 27-29, 2018, Proceedings, Lecture Notes in Computer Science, vol. 11159, Springer, pp. 65–78, arXiv:1707.01470, doi:10.1007/978-3-030-00256-5_6, S2CID 8008855
- ^ Lin, Lishin; Sahni, Sartaj (1989), "Fair edge deletion problems", IEEE Transactions on Computers, 38 (5): 756–761, doi:10.1109/12.24280, MR 0994519
- ^ Schwikowski, Benno; Speckenmeyer, Ewald (2002), "On enumerating all minimal solutions of feedback problems", Discrete Applied Mathematics, 117 (1–3): 253–265, doi:10.1016/S0166-218X(00)00339-5, MR 1881280
- ^ a b c Crescenzi, Pierluigi; Kann, Viggo; Halldórsson, Magnús; Karpinski, Marek; Woeginger, Gerhard (2000), "Minimum Feedback Arc Set", A compendium of NP optimization problems, archived from the original on 2021-07-29, retrieved 2021-07-29
- ^ Eades, Peter; Lin, Xuemin; Smyth, W. F. (1993), "A fast and effective heuristic for the feedback arc set problem", Information Processing Letters, 47 (6): 319–323, doi:10.1016/0020-0190(93)90079-O, MR 1256786, archived from the original on 2020-10-22, retrieved 2021-08-01
- ^ Berger, Bonnie; Shor, Peter W. (1997), "Tight bounds for the maximum acyclic subgraph problem", Journal of Algorithms, 25 (1): 1–18, doi:10.1006/jagm.1997.0864, MR 1474592
- ^ Hassin, Refael; Rubinstein, Shlomi (1994), "Approximations for the maximum acyclic subgraph problem", Information Processing Letters, 51 (3): 133–140, doi:10.1016/0020-0190(94)00086-7, MR 1290207
- ^ a b Newman, Alantha (June 2000), Approximating the maximum acyclic subgraph (Master’s thesis), Massachusetts Institute of Technology, hdl:1721.1/86548, 구루스와미 외(2011)에서 인용한 바와 같이.
- ^ a b Gabow, Harold N. (1995), "Centroids, representations, and submodular flows", Journal of Algorithms, 18 (3): 586–628, doi:10.1006/jagm.1995.1022, MR 1334365
- ^ a b Frank, András (1981), "How to make a digraph strongly connected", Combinatorica, 1 (2): 145–153, doi:10.1007/BF02579270, MR 0625547, S2CID 27825518
- ^ a b Lucchesi, C. L.; Younger, D. H. (1978), "A minimax theorem for directed graphs", Journal of the London Mathematical Society, Second Series, 17 (3): 369–374, doi:10.1112/jlms/s2-17.3.369, MR 0500618
- ^ a b Gabow, Harold N. (1993), "A framework for cost-scaling algorithms for submodular flow problems", 34th Annual Symposium on Foundations of Computer Science, Palo Alto, California, USA, 3-5 November 1993, IEEE Computer Society, pp. 449–458, doi:10.1109/SFCS.1993.366842, MR 1328441, S2CID 32162097
- ^ Grötschel, Martin; Jünger, Michael; Reinelt, Gerhard (1985), "On the acyclic subgraph polytope", Mathematical Programming, 33 (1): 28–42, doi:10.1007/BF01582009, MR 0809747, S2CID 206798683
- ^ Ramachandran, Vijaya (1988), "Finding a minimum feedback arc set in reducible flow graphs", Journal of Algorithms, 9 (3): 299–313, doi:10.1016/0196-6774(88)90022-3, MR 0955140
- ^ Kenyon-Mathieu, 클레어, Schudy, 워렌(2007년)," 어떻게 몇가지의 오류:PTAS과 가중 피드백 아크만 글로벌 톱에 토너먼트에 세트", 존슨, 데이비드 S.;Feige유리엘(eds.), 제39회 연간 ACM심포지움 이론 컴퓨팅, 샌 디에이고, 캘리포니아, 미국, 6월 11-13, 2007년에 회보를 대신하여 서명함. 95–103, doi:10.1145/1250790.1250806, S2CID 9436948, 유럽 사령부 협조 위원회.TR06-144, 보십시오 또한 작가의 확장판은 승객을 머신에 2009-01-15 Archived.
- ^ Arora, Sanjeev; Frieze, Alan; Kaplan, Haim (2002), "A new rounding procedure for the assignment problem with applications to dense graph arrangement problems", Mathematical Programming, 92 (1): 1–36, doi:10.1007/s101070100271, MR 1892295, S2CID 3207086, archived from the original on 2021-08-03, retrieved 2021-08-03
- ^ Karp, Richard M. (1972), "Reducibility among combinatorial problems", Complexity of Computer Computations, Proc. Sympos. IBM Thomas J. Watson Res. Center, Yorktown Heights, N.Y., New York: Plenum, pp. 85–103
- ^ Garey, Michael R.; Johnson, David S. (1979), "A1.1: GT8", Computers and Intractability: A Guide to the Theory of NP-Completeness, W.H. Freeman, p. 192, ISBN 0-7167-1045-5
- ^ Alon, Noga (2006), "Ranking tournaments", SIAM Journal on Discrete Mathematics, 20 (1): 137–142, doi:10.1137/050623905, MR 2257251
- ^ Charbit, Pierre; Thomassé, Stéphan; Yeo, Anders (2007), "The minimum feedback arc set problem is NP-hard for tournaments" (PDF), Combinatorics, Probability and Computing, 16 (1): 1–4, doi:10.1017/S0963548306007887, MR 2282830, S2CID 36539840
- ^ Ausiello, G.; D'Atri, A.; Protasi, M. (1980), "Structure preserving reductions among convex optimization problems", Journal of Computer and System Sciences, 21 (1): 136–153, doi:10.1016/0022-0000(80)90046-X, MR 0589808
- ^ Kann, Viggo (1992), On the Approximability of NP-complete Optimization Problems (PDF) (Ph.D. thesis), Department of Numerical Analysis and Computing Science, Royal Institute of Technology, Stockholm, archived (PDF) from the original on 2010-12-29, retrieved 2007-10-11
- ^ Dinur, Irit, Safra, 사무엘(2005년),"으로 최소 향점 덮개의 경도에"(PDF), 수학 연보, 162(1):439–485, doi:10.4007/annals.2005.162.439, 원본에서 2009-09-20에, 2021-07-29 회수된;(PDF)보관된 예비 버전에 Dinur, Irit, Safra, 사무엘(2002년),"편향되는 것의 중요성"에 Reif, 존 H..(교육.), 제34회 ACM심포지움 이론 컴퓨팅, 5월 19-21, 2002년, 몬트리올, 퀘벡, 캐나다, 회보를 대신하여 서명함. 33–42, doi:10.1145/509907.509915, S2CID 1235048.
- ^ Guruswami, Venkatesan; Håstad, Johan; Manokaran, Rajsekar; Raghavendra, Prasad; Charikar, Moses (2011), "Beating the random ordering is hard: every ordering CSP is approximation resistant" (PDF), SIAM Journal on Computing, 40 (3): 878–914, doi:10.1137/090756144, MR 2823511, archived (PDF) from the original on 2021-07-31, retrieved 2021-07-31
- ^ Bonnet, Édouard; Paschos, Vangelis Th. (2018), "Sparsification and subexponential approximation", Acta Informatica, 55 (1): 1–15, doi:10.1007/s00236-016-0281-2, MR 3757549, S2CID 3136275
- ^ Lovász, László (1976), "On two minimax theorems in graph", Journal of Combinatorial Theory, Series B, 21 (2): 96–103, doi:10.1016/0095-8956(76)90049-6, MR 0427138
- ^ Bar-Noy, Amotz; Naor, Joseph (1990), "Sorting, minimal feedback sets, and Hamilton paths in tournaments", SIAM Journal on Discrete Mathematics, 3 (1): 7–20, doi:10.1137/0403002, MR 1033709
- ^ Spencer, J. (1980), "Optimally ranking unrankable tournaments", Periodica Mathematica Hungarica, 11 (2): 131–144, doi:10.1007/BF02017965, MR 0573525, S2CID 119894999
- ^ Fernandez de la Vega, W. (1983), "On the maximum cardinality of a consistent set of arcs in a random tournament", Journal of Combinatorial Theory, Series B, 35 (3): 328–332, doi:10.1016/0095-8956(83)90060-6, MR 0735201
- ^ Barthélémy, Jean-Pierre; Hudry, Olivier; Isaak, Garth; Roberts, Fred S.; Tesman, Barry (1995), "The reversing number of a digraph", Discrete Applied Mathematics, 60 (1–3): 39–76, doi:10.1016/0166-218X(94)00042-C, MR 1339075
- ^ Isaak, Garth; Narayan, Darren A. (2004), "A classification of tournaments having an acyclic tournament as a minimum feedback arc set", Information Processing Letters, 92 (3): 107–111, doi:10.1016/j.ipl.2004.07.001, MR 2095357
- ^ Huang, Hao; Ma, Jie; Shapira, Asaf; Sudakov, Benny; Yuster, Raphael (2013), "Large feedback arc sets, high minimum degree subgraphs, and long cycles in Eulerian digraphs", Combinatorics, Probability and Computing, 22 (6): 859–873, arXiv:1202.2602, doi:10.1017/S0963548313000394, hdl:20.500.11850/73894, MR 3111546, S2CID 7967738
- ^ Hanauer, Kathrin; Brandenburg, Franz-Josef; Auer, Christopher (2013), "Tight upper bounds for minimum feedback arc sets of regular graphs", in Brandstädt, Andreas; Jansen, Klaus; Reischuk, Rüdiger (eds.), Graph-Theoretic Concepts in Computer Science - 39th International Workshop, WG 2013, Lübeck, Germany, June 19-21, 2013, Revised Papers, Lecture Notes in Computer Science, vol. 8165, Springer, pp. 298–309, doi:10.1007/978-3-642-45043-3_26, MR 3139198




 Hold-Karp 알고리즘
Hold-Karp 알고리즘

 와)
와)


 기본 비방향 그래프의
기본 비방향 그래프의 






















