멀티트리

Multitree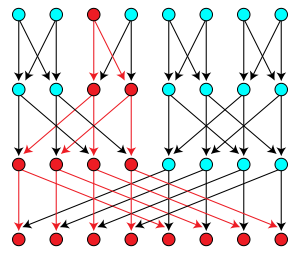
나비 네트워크는 분산 계산에 사용되는 다중 트리로서, 그 정점 중 하나에서 도달할 수 있는 서브그래프에 의해 유도된 비방향 트리를 빨간색으로 보여준다.
참고 항목: 멀티트리

조합학 및 순서 이론 수학에서, 다중 트리는 두 개의 등가 구조, 즉 두 꼭지점 사이에 최대 하나의 방향 경로가 있는 방향 아세클릭 그래프(DAG) 또는 어떤 꼭지점으로부터 하위 그래프가 도달할 수 있는 방향 또는 부분적으로 정렬된 세트(포지트) 중 하나를 설명할 수 있다. a, b, c, d 4개의 아이템이 다이아몬드 서브오더(diamond suborder)를 이루는 것은 아니지만 b와 c는 서로 비교가 안 된다(다이아몬드 프리 포셋이라고도[1] 한다).

계산 복잡성 이론에서, 다중 트리는 또한 강하게 모호하지 않은 그래프 또는 맹그로브라고도 불렸다; 그것들은 어떤 두 상태를 연결하는 최대 하나의 계산 경로가 있는 비결정론적인 알고리즘을 모델링하는 데 사용될 수 있다.[2]

다중 트리는 동일한 접지 세트에 걸쳐 여러 겹치는 분류법을 나타내기 위해 사용될 수 있다.[3] 한 가계도가 한 가족에서 다른 가족으로 복수 결혼을 포함할 수 있지만 두 혈족 간의 결혼은 포함하지 않는 경우, 그것은 다중 집단을 형성한다.[4]

DAG와 포지셋 정의 간의 동등성

지시된 아세클릭 그래프에서, 두 꼭지점 사이에 최대 하나의 방향 경로가 있거나, 또는 이와 동등하게 어떤 꼭지점에서 도달할 수 있는 하위 그래프가 비방향 트리를 유도하는 경우, 그 도달성 관계는 다이아몬드가 없는 부분 순서다. 반대로, 다이아몬드가 없는 경우 부분 순서로, 그 전이적 감소는 어떤 꼭지점에서든 서브그래프가 도달할 수 있는 방향의 아세클릭 그래프를 식별한다.

다이아몬드가 없는 패밀리

다이아몬드 없는 세트 제품군은 포함 순서가 다이아몬드 없는 포셋을 형성하는 F 제품군이다. 만약 D(n)가 n-element 세트의 가능한 가장 큰 다이아몬드 없는 부분 집합의 계열을 가리킨다면, 그것은 알려져 있다.

그리고 한계는 2라고 추측된다.[1]

관련 구조물

폴리트리(polytree)는 방향성이 없는 나무의 가장자리 방향을 정하여 형성된 방향의 악순환 그래프로서 다목수의 특수한 경우다.

다중 트리의 모든 정점에서 도달할 수 있는 하위 그래프는 정점에 뿌리를 둔 수목이며, 모든 가장자리가 뿌리에서 멀리 향하게 되는 폴리 트리다.

'다중류'라는 단어는 직렬 평행 부분 순서 [5]또는 복수의 나무를 조합하여 형성된 다른 구조물을 가리키는 말로도 사용되어 왔다.

참조

  1. ^ a b Griggs, Jerrold R.; Li, Wei-Tian; Lu, Linyuan (2010), Diamond-free families, arXiv:1010.5311, Bibcode:2010arXiv1010.5311G.
  2. ^ Allender, Eric; Lange, Klaus-Jörn (1996), "StUSPACE(log n) ⊆ DSPACE(log2 n/log log n)", Algorithms and Computation, 7th International Symposium, ISAAC '96, Osaka, Japan, December 16–18, 1996, Proceedings, Lecture Notes in Computer Science, 1178, Springer-Verlag, pp. 193–202, doi:10.1007/BFb0009495.
  3. ^ Furnas, George W.; Zacks, Jeff (1994), "Multitrees: enriching and reusing hierarchical structure", Proc. SIGCHI conference on Human Factors in Computing Systems (CHI '94), pp. 330–336, doi:10.1145/191666.191778, S2CID 18710118.
  4. ^ McGuffin, Michael J.; Balakrishnan, Ravin (2005), "Interactive visualization of genealogical graphs", IEEE Symposium on Information Visualization, Los Alamitos, CA, USA: IEEE Computer Society, p. 3, doi:10.1109/INFOVIS.2005.22, S2CID 15449409.
  5. ^ Jung, H. A. (1978), "On a class of posets and the corresponding comparability graphs", Journal of Combinatorial Theory, Series B, 24 (2): 125–133, doi:10.1016/0095-8956(78)90013-8, MR 0491356.