블록 암호

암호학에서 블록 암호는 블록이라고 불리는 고정 길이의 비트 그룹에서 작동하는 결정론적 알고리즘입니다.이들은 많은 암호화 프로토콜 설계에서 지정된 기본 구성 요소이며 데이터 교환 프로토콜을 포함하여 많은 양의 데이터를 암호화하는 데 널리 사용됩니다.블록은 변하지 않는 변환으로 사용됩니다.

보안 블록 암호도 고정 키를 사용하여 한 번에 하나의 데이터 블록만 암호화하는 데 적합합니다.기밀성과 신뢰성이라는 보안 목표를 달성하기 위해 안전한 방법으로 반복적으로 사용할 수 있도록 많은 운영 모드가 설계되어 있습니다.그러나 블록 암호는 범용 해시 함수 및 의사 난수 생성기와 같은 다른 암호화 프로토콜에서 구성 블록으로도 기능할 수 있습니다.

정의.

블록 암호는 2개의 페어링된 알고리즘으로 구성됩니다.하나는 암호화용이고,E다른 하나는 복호화용입니다.D두 알고리즘 모두 2개의 입력을 받아들입니다.^[1]크기의 입력 블록n비트와 크기의 키kbits; 그리고 둘 다,n- 비트 출력 블록복호화 알고리즘D암호화의 역함수(예: $=)$ 로 정의됩니다. 더 공식적으로 ^[2]^[3]블록 암호는 암호화 함수에 의해 지정됩니다.

E_{K}(P):=E(K,P):\{0,1\}^{k}\times \{0,1\}^{n}\오른쪽 화살표 \{0,1\}^{n}

이것은 입력으로 키를 받아들인다.K, 비트 길이의k(키 사이즈라고 불립니다) 및 비트 문자열P, 길이n(블록 크기라고 함) 및 문자열을 반환합니다.C의n비트를 클릭합니다.P를 보통 텍스트라고 부릅니다.C를 암호문이라고 부릅니다.각각에 대해서K, 함수E_K( )P $)$ 는 { $0,1} n$ 에서 $반전$ 매핑이어야 합니다.의 역수E함수로 정의됩니다.

E_{K}^{-1}(C):=D_{K}(C)=D(K,C):\{0,1\}^{k}\times \{0,1\}^{n}\rightarrow \{0,1\}^{n

키잡기K및 암호문C평문 값을 반환하다P그렇게 해서

\displaystyle \forall K:D_{K}(E_{K}(P)=P.}

예를 들어 블록 암호 암호화 알고리즘은 128비트 플레인텍스트 블록을 입력으로 받아 대응하는 128비트 암호텍스트 블록을 출력할 수 있습니다.정확한 변환은 두 번째 입력인 개인 키를 사용하여 제어됩니다.복호화도 비슷합니다.이 예에서는 복호화 알고리즘이 비밀키와 함께 128비트 암호문 블록을 사용하여 원래 128비트 일반 ^[4]텍스트 블록을 생성합니다.

각 키 K에 대해 E는_K 입력 블록 세트에 대한 치환(바이오젝티브 매핑)입니다.각 키는 $(2^{n})!$ ( $(2^{n})!$ n $)!\displaystyle(2^{n})$ 세트 중에서 하나의 치환을 선택합니다.}개의 $(2^{n})!$ 가능한 순열 $.$ ^[5]

역사

블록 암호의 현대적 설계는 반복 제품 암호의 개념을 기반으로 합니다.클로드 섀넌은 1949년에 출판된 자신의 저서 '비밀 시스템의 커뮤니케이션 이론'에서 제품 암호를 분석하여 치환과 ^[6]치환과 같은 간단한 연산을 결합함으로써 효과적으로 보안을 향상시키는 수단으로 제안했습니다.반복된 제품 암호는 여러 라운드로 암호화를 수행하며, 각 암호는 원래 키에서 파생된 서로 다른 하위 키를 사용합니다.이러한 암호의 광범위한 구현 중 하나는 Horst Feistel의 이름을 딴 Feistel 네트워크이며, DES ^[7]암호에 특히 구현되어 있습니다.AES 등 블록 암호의 다른 많은 실현은 대체 ^[8]Permutation 네트워크로 분류됩니다.

PCI DSS(Payment Card Industry Data Security Standard) 및 ANSI(American National Standards Institute) 표준 내에서 사용되는 모든 암호화 블록 포맷의 근원은 최초의 하드웨어 보안 모듈(HSM)인 Atalla Box의 주요 혁신 기술인 AKB(Atalla Key Block)에 있습니다.그것은 1972년 모하메드 M에 의해 개발되었다. Atalla Corporation(현 Utimaco Atalla)의 설립자 Atalla, 1973년에 발매.AKB는 대칭 키 또는 PIN을 은행 업계의 다른 관계자들과 안전하게 교환하는 데 필요한 핵심 블록이었습니다.이 안전한 교환은 AKB 형식을 사용하여 수행됩니다.^[9]Atalla Box는 1998년 ^[10]현재 운영 중인 모든 ATM 네트워크의 90% 이상을 보호하고 있으며,^[11] Atalla 제품은 2014년 현재도 전 세계 ATM 거래의 대부분을 보호하고 있습니다.

1977년 미국 국립표준국(이후 미국 국립표준기술원, NIST)에 의한 DES 암호의 발행은 현대 블록 암호 설계에 대한 대중의 이해의 기초였다.그것은 또한 암호 해독 공격의 학문적 발전에 영향을 미쳤다.DES 설계에 관한 연구로부터 미분 및 선형 암호해석이 모두 생겨났다.2016년 현재^[update] 블록 암호는 무차별 공격에 대해 견고할 뿐만 아니라 보안도 확보해야 하는 다양한 공격 기술이 있습니다.

설계.

반복된 블록 암호

대부분의 블록 암호 알고리즘은 반복 블록 암호로 분류됩니다. 즉, 라운드 함수로 알려진 반전 변환의 반복 적용을 통해 평문의 고정 크기 블록을 동일한 크기의 암호 텍스트 블록으로 변환하고 각 반복을 ^[12]라운드라고 합니다.

보통 라운드 함수 R은 원래 ^{[citation needed]}키에서 파생된 다른 라운드 키 K를_i 두 번째 입력으로 받아들입니다.

{displaystyle M_{i}=R_{K_{i}}(M_{i-1})

$M_{0}$ 서 M 0 $({$ 은 $M_{0}$ 평문, $M_{r}$ r $({$ 은 $M_r$ 암호문이며 r은 라운드의 수입니다.

키 화이트닝은 이 외에도 자주 사용됩니다.처음과 마지막에는 주요 자료로 데이터를 수정합니다(종종 XOR를 사용하지만 더하기 및 빼기와 같은 간단한 산술 연산도 사용됩니다).^{[citation needed]}

M_{0}=M\oplus K_{0}

{displaystyle M_{i}=R_{K_{i}}(M_{i-1})\;;i=1\dots r}

C=M_{r}\oplus K_{r+1

표준적인 반복 블록 암호 설계 방식 중 하나를 사용하면 많은 라운드를 사용하는 것만으로 암호학적으로 안전한 블록 암호를 구축하는 것이 매우 쉽습니다.단, 이로 인해 암호의 효율이 떨어집니다.따라서 효율성은 전문 암호에 대한 가장 중요한 추가 설계 기준입니다.또한 양호한 블록 암호는 캐시 상태 또는 실행 시간을 통해 비밀 데이터가 누출될 수 있는 분기 예측 및 입력 의존 메모리 액세스 등의 사이드 채널 공격을 회피하도록 설계되어 있습니다.또, 소규모의 하드웨어와 소프트웨어의 실장에서는, 암호는 간결하게 할 필요가 있습니다.마지막으로 암호는 쉽게 암호 분석을 할 수 있어야 합니다.이것에 의해, 기존의 암호 공격이 기능하기 위해서, 또 반대로, 실제의 회수는,^{[citation needed]} 암호로부터 보호할 수 있을 만큼 충분히 많다는 것을 알 수 있습니다.

대체 - 주변 네트워크

16비트의 평문 블록을 16비트의 암호문 블록으로 암호화하는 3라운드의 대체-변환 네트워크 스케치.S박스는 S_i, P박스는 같은 P, 라운드 키는 K입니다_i.

Substitution-Permutation Network(SPN; 대체변환 네트워크)라고 불리는 중요한 유형의 반복 블록 암호는 평문과 키의 블록을 입력으로 하여 치환 단계와 치환 단계로 이루어진 여러 라운드를 번갈아 ^[13]적용하여 암호문 출력의 각 블록을 생성합니다.비선형 치환 단계는 키 비트와 평문의 비트를 혼합하여 섀넌의 혼란을 일으킨다.그런 다음 선형 순열 단계는 중복을 소멸시켜 ^[14]^[15]확산을 생성합니다.

대체 상자(S 상자)는 입력 비트의 작은 블록을 다른 출력 비트 블록으로 대체합니다.반전성을 확보하기 위해 이 치환은 1대 1이어야 합니다(따라서 복호화).시큐어 S박스는 1개의 입력 비트를 변경하면 평균 출력 비트의 절반 정도가 변경되어 눈사태 효과로 알려진 것이 나타납니다. 즉, 각 출력 비트가 모든 입력 ^[16]비트에 의존한다는 특성이 있습니다.

치환상자(P박스)는 모든 비트의 치환입니다.한 라운드의 모든 S박스의 출력을 가져와 비트를 치환한 후 다음 라운드의 S박스로 보냅니다.양호한 P박스는 S박스의 출력 비트가 가능한 ^{[citation needed]}한 많은 S박스 입력에 분배되는 특성을 가진다.

라운드 키(예를 들어 S박스 및 P박스 사용 등 간단한 조작으로 키에서 얻은 것)는 각 라운드에서 그룹 조작(일반적으로 XOR)^{[citation needed]}을 사용하여 결합됩니다.

복호화는 단순히 프로세스를 반대로 하는 것만으로 이루어집니다(S박스 및 P박스의 역순으로 ^[17]라운드 키를 적용).

페이스텔 암호

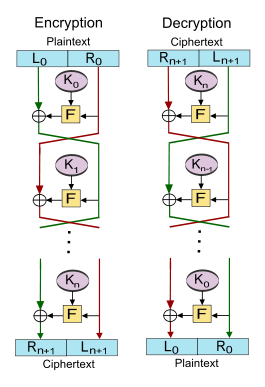
DES 및 Blowfish와 같은 많은 블록 암호는 Feistel 암호로 알려진 구조를 사용합니다.

파이스텔 암호는 암호화되는 플레인 텍스트 블록을 2개의 동일한 크기의 반으로 분할한다.라운드 함수는 서브키를 사용하여 한쪽 절반에 적용되며, 다음으로 출력은 다른 한쪽 절반과 XOR됩니다.그 후, 2개의 반이 ^[18]교환됩니다.

F $(\$ 를 ${\rm F}$ 라운드 함수로 $K_{0},K_{1},\ldots ,K_{n}$ $Kn$ $(\$ $displaystyle$ K_ ${0},$ 를 $K_0,K_1,\ldots,K_{n}$ $0,1,\ldots ,n$ 0 $0,1,\ldots ,n$ , $0,1,\ldots ,n$ (\ $displaystyle$ 0, $0,1,\ldots ,n$ 1,\ $ldots, n)$ 의 $0,1,\ldots,n$ 서브 키로 $K_{0},K_{1},\ldots ,K_{n}$ .

다음으로 기본 조작은 다음과 같습니다.^[18]

플레인 텍스트블록을 $L_{0}$ 한다( L $L_{0}$ { $displaystyle$ L _ { $0$ } 、 $R_{0}$ 0 \ $displaystyle R$ _ { $0$ } ）

각 $i=0,1,\dots ,n$ i $i=0,1,\dots ,n$ , $i=0,1,\dots ,n$ , $i=0,1,\dots ,n$ , $i=0,1,\dots ,n$ \ $displaystyle$ i $= 0$ , 1 $,$ $\ displaystyle$ , $n$ } , compute

L_{i+1}=R_{i},

R

i +

R_{i+1}=L_{i}\oplus {\rm {F}}(R_{i},K_{i})

R_{i+1}=L_{i}\oplus {\rm {F}}(R_{i},K_{i})

R_{i+1}=L_{i}\oplus {\rm {F}}(R_{i},K_{i})

i

R_{i+1}=L_{i}\oplus {\rm {F}}(R_{i},K_{i})

F (

R_{i+1}=L_{i}\oplus {\rm {F}}(R_{i},K_{i})

,

R_{i+1}=L_{i}\oplus {\rm {F}}(R_{i},K_{i})

) {

displaystyle R

_ {

i

} =

L

_ {

i

} \

oplus

{

F

} （

R

_ {

i

,

K

_ { i

R_{i+1}=L_{i}\oplus {\rm {F}}(R_{i},K_{i})

。

다음으로 암호문은 ( $(R_{n+1},L_{n+1})$ n + $(R_{n+1},L_{n+1})$ , $(R_{n+1},L_{n+1})$ n + $)({ displaystyle$ ( $R_{n+1$ }, $L_{n+$ 1})입니다 $(R_{n+1},L_{n+1})$

암호문 $(R_{n+1},L_{n+1})$ $(R_{n+1},L_{n+1})$ n + $(R_{n+1},L_{n+1})$ , $(R_{n+1},L_{n+1})$ n + $(R_{n+1},L_{n+1})$ $)({$ $displaystyle (R_{n+1}, L_{n+1})$ 의 $(R_{n+1}, L_{n+1})$ 복호화는 i $i=n,n-1,\ldots ,0$ $i=n,n-1,\ldots ,0$ - $i=n,n-1,\ldots ,0$ $i=n,n-1,\ldots ,0$ $({displaystyle$ i $=n, n-1,\ldots,0})$ 의 연산에 의해 이루어집니다.

R_{i}=L_{i+1},

L_{i}=R_{i+1}\oplus {\rm {F}}(L_{i+1},K_{i})

L_{i}=R_{i+1}\oplus {\rm {F}}(L_{i+1},K_{i})

L_{i}=R_{i+1}\oplus {\rm {F}}(L_{i+1},K_{i})

+

L_{i}=R_{i+1}\oplus {\rm {F}}(L_{i+1},K_{i})

F (

L_{i}=R_{i+1}\oplus {\rm {F}}(L_{i+1},K_{i})

+

L_{i}=R_{i+1}\oplus {\rm {F}}(L_{i+1},K_{i})

,

L_{i}=R_{i+1}\oplus {\rm {F}}(L_{i+1},K_{i})

) {

displaystyle L_{

i}

= R_{i+1}\oplus {F}

(

L_{i+1}, K_{i

$(L_{0},R_{0})$ 으로 $(L_{0},R_{0})$ ( $(L_{0},R_{0})$ $(L_{0},R_{0})$ , $(L_{0},R_{0})$ 0 $(L_{0},R_{0})$ ) { $displaystyle$ ( $L$ _ { 0 , R _ { $0$ } )는 $(L_{0},R_{0})$ 다시 보통 텍스트가 됩니다.

대체-변환 네트워크와 비교하여 Feistel 모델의 장점 중 하나는 라운드 ${\rm {F}}$ F(\style $\display\rm$ { $F})$ 를 ${\rm F}$ ^[19]반전시킬 필요가 없다는 것입니다.

라이-매시 암호

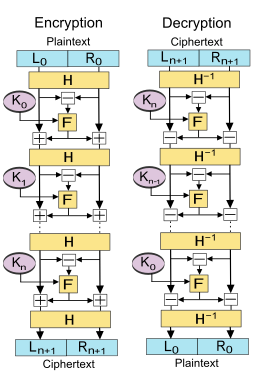
Lai-Massey 스킴.이것을 이용한 전형적인 암호는 IDEA입니다.

Lai-Massey 스킴은 Feistel 구조와 유사한 보안 속성을 제공합니다.또한 라운드 $\mathrm {F}$ F $(\$ 를 $\mathrm F$ 반전시킬 필요가 없다는 장점도 있습니다.또 다른 유사점은 입력 블록을 2개의 동일한 조각으로 분할한다는 것입니다.단, 둘 사이의 차이에 라운드 함수를 적용하여 그 결과를 양쪽 하프 블록에 가산한다.

F $(\$ 를 $\mathrm F$ 라운드 함수, $\mathrm {H}$ H(\ $displaystyle \mathrm {H})$ 를 $\mathrm H$ 하프라운드 함수, $(\$ $displaystyle$ $K_{0},$ ${$ $n$ })을 $K_0,K_1,\ldots,K_n$ 0 $,$ 의 $0,1,\ldots ,n$ 서브키라고 $\mathrm {F}$ $0,1,\ldots ,n$

다음으로 기본 조작은 다음과 같습니다.

플레인 텍스트블록을 $L_{0}$ 한다( L $L_{0}$ { $displaystyle$ L _ { $0$ } 、 $R_{0}$ 0 \ $displaystyle R$ _ { $0$ } ）

각 $i=0,1,\dots ,n$ i $i=0,1,\dots ,n$ , $i=0,1,\dots ,n$ , $i=0,1,\dots ,n$ , $i=0,1,\dots ,n$ \ $displaystyle$ i $= 0$ , 1 $,$ $\ displaystyle$ , $n$ } , compute

(\displaystyle(L_{i+1}), R_{i+1})=\mathrm {H} (L_{i}'+)T_{i}, R_{i}'+T_{i}},}

$T_{i}=\mathrm {F} (L_{i}'-R_{i}',K_{i})$ 서 $T_{i}=\mathrm {F} (L_{i}'-R_{i}',K_{i})$ $T_{i}=\mathrm {F} (L_{i}'-R_{i}',K_{i})$ ( $T_{i}=\mathrm {F} (L_{i}'-R_{i}',K_{i})$ i $T_{i}=\mathrm {F} (L_{i}'-R_{i}',K_{i})$ - $T_{i}=\mathrm {F} (L_{i}'-R_{i}',K_{i})$ $T_{i}=\mathrm {F} (L_{i}'-R_{i}',K_{i})$ $T_{i}=\mathrm {F} (L_{i}'-R_{i}',K_{i})$ , $T_{i}=\mathrm {F} (L_{i}'-R_{i}',K_{i})$ K $T_{i}=\mathrm {F} (L_{i}'-R_{i}',K_{i})$ ) { $displaystyle T_$ {i}=\ $mathrm {F} (L_$ { $(L_{0}',R_{0}')=\mathrm {H} (L_{0},R_{0})$ $}, K_{i})$ 및 (L $(L_{0}',R_{0}')=\mathrm {H} (L_{0},R_{0})$ 0 $display$ $(L_{0}',R_{0}')=\mathrm {H} (L_{0},R_{0})$ $(L_{0}',R_{0}')=\mathrm {H} (L_{0},R_{0})$ $(L_{0}',R_{0}')=\mathrm {H} (L_{0},R_{0})$ display $(L_{0}',R_{0}')=\mathrm {H} (L_{0},R_{0})$ $(L_{0}',R_{0}')=\mathrm {H} (L_{0},R_{0})$ ( $L$ 0 , $(L_{0}',R_{0}')=\mathrm {H} (L_{0},R_{0})$ _ 0 _ $display)$

다음으로 암호문은 ( $(L_{n+1},R_{n+1})=(L_{n+1}',R_{n+1}')$ n + $(L_{n+1},R_{n+1})=(L_{n+1}',R_{n+1}')$ , $(L_{n+1},R_{n+1})=(L_{n+1}',R_{n+1}')$ n + $(L_{n+1},R_{n+1})=(L_{n+1}',R_{n+1}')$ ) $(L_{n+1},R_{n+1})=(L_{n+1}',R_{n+1}')$ ( $(L_{n+1},R_{n+1})=(L_{n+1}',R_{n+1}')$ + $(L_{n+1},R_{n+1})=(L_{n+1}',R_{n+1}')$ , $(L_{n+1},R_{n+1})=(L_{n+1}',R_{n+1}')$ $(L_{n+1},R_{n+1})=(L_{n+1}',R_{n+1}')$ + 1 $(L_{n+1},R_{n+1})=(L_{n+1}',R_{n+1}')$ ) ( $L _$ { $n$ + $1$ ) $=$ ( L _ { n + 1 ) , $R$ _ { $n$ + $1$ } ) $(L_{n+1},R_{n+1})=(L_{n+1}',R_{n+1}')$ = ( L _ { $n$ + 1 } ) 。

암호문 $(L_{n+1},R_{n+1})$ $(L_{n+1},R_{n+1})$ n + $(L_{n+1},R_{n+1})$ , R $(L_{n+1},R_{n+1})$ + $(L_{n+1},R_{n+1})$ $)({$ $displaystyle (L_{n+1}, R_{n+1})$ 의 $(L_{n+1}, R_{n+1})$ 복호화는 i $i=n,n-1,\ldots ,0$ , $i=n,n-1,\ldots ,0$ - $i=n,n-1,\ldots ,0$ , $i=n,n-1,\ldots ,0$ … $i=n,n-1,\ldots ,0$ , $i=n,n-1,\ldots ,0$ { $displaystyle$ i $= n$ , $n$ - 1 , $\ldots$ , 0 $i=n,n-1,\ldots ,0$ } 의 $i=n,n-1,\ldots ,0$ 에 의해 이루어집니다.

{\displaystyle (L_{i}), R_{i}'=\mathrm {H}^{-1}(L_{i+1}-T_{i}, R_{i+1}-T_{i})

$T_{i}=\mathrm {F} (L_{i+1}'-R_{i+1}',K_{i})$ 서 $T_{i}=\mathrm {F} (L_{i+1}'-R_{i+1}',K_{i})$ $T_{i}=\mathrm {F} (L_{i+1}'-R_{i+1}',K_{i})$ ( $T_{i}=\mathrm {F} (L_{i+1}'-R_{i+1}',K_{i})$ + $T_{i}=\mathrm {F} (L_{i+1}'-R_{i+1}',K_{i})$ $T_{i}=\mathrm {F} (L_{i+1}'-R_{i+1}',K_{i})$ - $T_{i}=\mathrm {F} (L_{i+1}'-R_{i+1}',K_{i})$ i + $T_{i}=\mathrm {F} (L_{i+1}'-R_{i+1}',K_{i})$ , , $T_{i}=\mathrm {F} (L_{i+1}'-R_{i+1}',K_{i})$ i ) $T_{i}=\mathrm {F} (L_{i+1}'-R_{i+1}',K_{i})$ { $display style$ T_ ${i$ }=\ $mathrm {F}$ ( $L_{i+$ 1}- $R_{$ i}}, $(L_{n+1}',R_{n+1}')=\mathrm {H} ^{-1}(L_{n+1},R_{n+1})$ K_ $(L_{n+1}',R_{n+1}')=\mathrm {H} ^{-1}(L_{n+1},R_{n+1})$ i}}}) 및 $T_{i}=\mathrm {F} (L_{i+1}'-R_{i+1}',K_{i})$ ( $(L_{n+1}',R_{n+1}')=\mathrm {H} ^{-1}(L_{n+1},R_{n+1})$ + $(L_{n+1}',R_{n+1}')=\mathrm {H} ^{-1}(L_{n+1},R_{n+1})$ $(L_{n+1}',R_{n+1}')=\mathrm {H} ^{-1}(L_{n+1},R_{n+1})$ + $(L_{n+1}',R_{n+1}')=\mathrm {H} ^{-1}(L_{n+1},R_{n+1})$ $(L_{n+1}',R_{n+1}')=\mathrm {H} ^{-1}(L_{n+1},R_{n+1})$ R + 1 $(L_{n+1}',R_{n+1}')=\mathrm {H} ^{-1}(L_{n+1},R_{n+1})$ ′, $(L_{n+1}',R_{n+1}')=\mathrm {H} ^{-1}(L_{n+1},R_{n+1})$ + 1 ′, R ), R ′, Ki $(L_{n+1}',R_{n+1}')=\mathrm {H} ^{-1}(L_{n+1},R_{n+1})$ 1 （ 1 ） - $(L_{n+1}',R_{n+1}')=\mathrm {H} ^{-1}(L_{n+1},R_{n+1})$ （ $(L_{n+1}',R_{n+1}')=\mathrm {H} ^{-1}(L_{n+1},R_{n+1})$ ） - H $(L_{n+1}',R_{n+1}')=\mathrm {H} ^{-1}(L_{n+1},R_{n+1})$ 1 （ 1 ））（ 1 ））（ 1 ））） $=\mathrm {H} ^{-1}(L_{n+1},R_{n+1})}$

$(L_{0},R_{0})=(L_{0}',R_{0}')$ 으로 ( $(L_{0},R_{0})=(L_{0}',R_{0}')$ $(L_{0},R_{0})=(L_{0}',R_{0}')$ , $(L_{0},R_{0})=(L_{0}',R_{0}')$ 0 ) $(L_{0},R_{0})=(L_{0}',R_{0}')$ ( $(L_{0},R_{0})=(L_{0}',R_{0}')$ 0 $(L_{0},R_{0})=(L_{0}',R_{0}')$ , $(L_{0},R_{0})=(L_{0}',R_{0}')$ 0 ${\$ ) { $displaystyle$ ( L $_$ { 0 , R _ { 0 ) = ( L _ $0$ } , $R$ _ { $0$ )는 $(L_{0},R_{0})=(L_{0}',R_{0}')$ 평문입니다.

운용

ARX(추가 회전 X)또는)

현대의 많은 블록 암호 및 해시는 ARX 알고리즘입니다. 라운드 함수에는 (A) 모듈러 추가, (R) 고정 회전량 및 (X) XOR의 세 가지 연산만 포함됩니다. 예를 들어 ChaCha20, Spec, XXTEA 및 BLAKE 등이 있습니다.많은 저자들이 이러한 둥근 ^[20]함수를 설명하기 위해 데이터 흐름도의 일종인 ARX 네트워크를 그린다.

이러한 ARX 조작은 하드웨어 및 소프트웨어에서 비교적 빠르고 저렴하며 구현이 매우 간단하며 일정 시간 내에 실행되므로 타이밍 공격에 영향을 받지 않기 때문에 인기가 있습니다.회전 암호 해독 기술은 이러한 라운드 함수를 공격하려고 시도합니다.

기타 작업

블록 암호에 자주 사용되는 다른 작업으로는 RC5 및 RC6와 같이 데이터에 의존하는 회전, Data Encryption Standard 및 Advanced Encryption Standard와 같이 룩업 테이블로 구현된 대체 상자, IDEA와 같이 치환 상자, 곱셈 등이 있습니다.

동작 모드

전자 코드북(ECB) 모드 부호화의 결과로서 이미지의 안전하지 않은 암호화.

블록 암호 자체는 암호 블록 길이의 단일 데이터 블록만 암호화할 수 있습니다.가변 길이 메시지의 경우 먼저 데이터를 별도의 암호 블록으로 분할해야 합니다.전자코드북(ECB) 모드로 알려진 가장 간단한 경우 메시지는 먼저 암호 블록 크기의 개별 블록(패딩 비트로 마지막 블록을 확장 가능)으로 분할된 후 각 블록이 독립적으로 암호화 및 복호화됩니다.단, 이러한 순진한 방법은 일반적으로 안전하지 않습니다.이는 동일한 평문 블록이 항상 동일한 암호문 블록(같은 키에 대해)을 생성하기 때문입니다.따라서 평문 메시지 내의 패턴이 암호문 ^[21]출력으로 명확하게 나타나기 때문입니다.

이 제한을 극복하기 위해 NIST 800-38A^[24] 및 BSI TR-02102와^[25] 같은 국가 권장사항 및 ISO/IEC 10116과 ^[26]같은 국제 표준에 이른바 블록 암호 모드가 설계^[22]^[23] 및 지정되었습니다.일반적인 개념은 종종 초기화 벡터라고 불리는 추가 입력 값에 기초한 평문 데이터의 랜덤화를 사용하여 확률적 ^[27]암호화라고 불리는 것을 만드는 것이다.Public Cipher Block Chaining(CBC; 일반 암호 블록 체인) 모드에서 암호화를 확보하려면 평문 메시지와 함께 전달되는 초기화 벡터가 랜덤 또는 의사 랜덤 값이어야 하며, 이 값은 암호화되기 전에 첫 번째 평문 블록에 배타적 또는 방식으로 부가됩니다.그 결과 생성된 암호문 블록은 다음 평문 블록의 새로운 초기화 벡터로 사용됩니다.자기동기 스트림 암호를 에뮬레이트하는 암호 피드백(CFB) 모드에서는 우선 초기화 벡터가 암호화되어 평문 블록에 부가된다.Output Feedback(OFB; 출력 피드백) 모드에서는 초기화 벡터가 반복적으로 암호화되어 동기 스트림 암호 에뮬레이션용 키스트림이 생성됩니다.새로운 카운터(CTR) 모드에서도 마찬가지로 키 스트림이 생성되지만 초기화 벡터로 필요한 것은 고유하고 (의사가 아닌) 랜덤 값뿐이라는 장점이 있습니다.필요한 랜덤성은 초기화 벡터를 블록카운터로 사용하여 각 ^[24]블록에 대해 이 카운터를 암호화함으로써 내부적으로 도출됩니다.

보안 이론의 관점에서 운용 모드는 의미 보안이라고 알려진 ^[28]것을 제공해야 합니다.비공식적으로 알 수 없는 키 아래에 있는 일부 암호문이 주어지면 암호문을 보지 않고는 알 수 없었던 암호문으로부터 (메시지 길이 이외의) 정보를 실질적으로 도출할 수 없다는 것을 의미합니다.위에서 설명한 모든 모드는 ECB 모드를 제외하고 소위 선택된 평문 공격 하에서 이 속성을 제공하는 것으로 나타났다.

패딩

CBC 모드 등의 일부 모드는 완전한 플레인텍스트블록에서만 동작합니다.메시지의 마지막 블록을 0비트로 확장하는 것만으로는 수신자가 패딩 비트의 양만 다른 메시지를 쉽게 식별할 수 없기 때문에 충분하지 않습니다.더 중요한 것은 이러한 단순한 솔루션이 매우 효율적인 패딩 오라클 ^[29]공격을 발생시킨다는 점입니다.따라서 마지막 평문 블록을 암호 블록 크기로 확장하려면 적절한 패딩 방식이 필요합니다.표준 및 문헌에 설명된 많은 일반적인 스킴이 패딩 오라클 ^[29]^[30]공격에 취약한 것으로 나타났지만 ISO/IEC 9797-1에서 ^[31]"패딩 방법 2"로 표준화된 1비트를 추가한 다음 제로 비트로 마지막 블록을 확장하는 솔루션이 이러한 ^[30]공격에 대해 안전한 것으로 입증되었습니다.

암호 분석

무차별 공격

이 속성으로 인해 암호의 보안이 2차적으로 저하되므로 블록 크기를 선택할 때 고려해야 합니다.그러나 블록 크기가 크면 알고리즘이 비효율적으로 ^[32]작동할 수 있기 때문에 단점이 있습니다.DES 등의 이전 블록 암호는 일반적으로 64비트 블록 크기를 선택했지만 AES 등의 새로운 설계에서는 128비트 이상의 블록 크기를 지원하며 일부 암호는 다양한 블록 ^[33]크기를 지원합니다.

암호

선형 암호해석은 암호의 작용에 대한 아핀 근사치를 찾는 것에 기초한 암호해석의 한 형태입니다.선형 암호 분석은 블록 암호에 대해 가장 널리 사용되는 두 가지 공격 중 하나이며, 다른 하나는 차등 암호 ^[34]분석입니다.

이 발견은 FEAL 암호(Matsui and Yamagishi,^[35] 1992년)에 이 기술을 처음 적용한 마쓰이 미쓰루 덕분이다.

Integrated Cryptanalysis는 치환 네트워크를 기반으로 한 블록 암호에 특히 적용되는 암호 분석 공격입니다.고정 XOR 차이를 가진 선택된 평문의 쌍을 사용하는 차등 암호 분석과 달리, 통합 암호 분석은 선택된 평문의 집합 또는 심지어 멀티셋을 사용합니다. 이 집합의 일부는 일정하게 유지되고 다른 부분은 모든 가능성을 통해 다릅니다.예를 들어, 공격은 8비트를 제외한 모든 비트가 동일한 256개의 선택된 플레인텍스트를 사용할 수 있습니다.단, 이들 8비트는 모두 다릅니다.이러한 집합은 반드시 0의 XOR 합계를 가지며, 대응하는 암호문 집합의 XOR 합계는 암호의 연산에 관한 정보를 제공한다.텍스트 쌍의 차이와 더 큰 텍스트 세트의 합 사이의 이러한 대조는 미적분학의 용어를 ^{[citation needed]}차용하여 "통합 암호 분석"이라는 이름에 영감을 주었다.

부메랑 공격의 발달로 그동안 차분 공격에 대해 안전하다고 여겨졌던 많은 암호에 차분 암호 해독 기술을 적용할 수 있게 되었다.

선형 및 차등 암호 분석 외에도 잘린 차등 암호 분석, 부분 차등 암호 분석, 사각 및 적분 공격, 슬라이드 공격, 부메랑 공격, XSL 공격, 불가능한 차등 암호 분석 및 대수 공격 등의 공격 카탈로그가 증가하고 있습니다.새로운 블록 암호 설계가 신뢰성을 가지려면 기존의 ^{[citation needed]}공격에 대한 보안의 증거를 제시해야 합니다.

(보안)

특정 동작 모드에서 블록 암호를 사용하는 경우 결과 알고리즘은 블록 암호 자체만큼 안전해야 합니다.ECB(상기 설명)에는 이 속성이 없습니다.기본 블록 암호의 보안에 관계없이 ECB 모드는 쉽게 공격받을 수 있습니다.한편, CBC 모드는 기반이 되는 블록 암호도 마찬가지로 안전하다는 전제 하에 안전하다는 것을 증명할 수 있습니다.단, 이와 같은 스테이트먼트를 작성하려면 암호화 알고리즘 또는 블록 암호의 의미에 대한 공식적인 수학적 정의가 필요합니다.이 항에서는 블록 암호의 속성에 대한 두 가지 일반적인 개념에 대해 설명합니다.각각은 CBC와 같은 상위 수준의 알고리즘의 속성을 증명하기 위해 사용할 수 있는 수학적 모델에 해당합니다.

이러한 암호화에 대한 일반적인 접근법(CBC 등)은 컴포넌트(블록 암호 등)에 관해 명시적으로 기술된 전제조건 하에서 안전하다는 것을 증명하는 것)을 증명 가능한 보안이라고 합니다.

★★★★★

비공식적으로 공격자가 블록 암호(랜덤 키 포함)와 랜덤 순열을 구별할 수 없는 경우 블록 암호는 표준 모델에서 안전합니다.

좀 더 정확하게 말하면 E를 n비트블록 암호로 하겠습니다다음과 같은 게임을 상정합니다.

게임을 하는 사람이 동전을 던집니다.
- 동전이 앞면에 착지하면, 임의의 키 K를 선택하고 함수 f = E를_K 정의합니다.
- 동전이 꼬리에 착지하는 경우, 그는 n비트 문자열 집합에서 랜덤 치환 $θ$ 를 선택하고 f = $θ$ 함수를 정의한다.
공격자는 n비트 문자열 X를 선택하고 게임을 실행하는 사람이 f(X) 값을 알려줍니다.
스텝 2는 총 q회 반복됩니다.(이러한 q의 상호작용은 각각 쿼리입니다.)
공격자는 동전이 어떻게 떨어졌는지 추측한다.을 사용법

알고리즘으로 모델링할 수 있는 공격자를 대항마라고 부릅니다.f(적수가 쿼리할 수 있었던 함수)를 oracle이라고 합니다.

상대는 무작위로 추측하는 것(예를 들어 항상 "앞면"을 추측하는 것)만으로 50%의 확률로 승리할 수 있다는 점에 유의하십시오.따라서 P(A)는_E 상대 A가 E에 대해 이 게임에서 이길 확률을 나타내며 A의 장점을 2(P_E(A) - 1/2)로 정의한다.따라서 A가 무작위로 추측하면 장점이 0이 되고, 반대로 A가 항상 이기면 장점이 1이 됩니다.블록 암호E는 상대방이 0보다 훨씬 큰 이점을 갖지 않는 경우 Pseudo-Random Permutation(PRP; 의사랜덤순열)이 됩니다.이는 q와 상대편의 실행시간에 대한 특정 제한이 있기 때문입니다.위의 2단계에서 상대방이 f(X) 대신 f(X)를⁻¹ 학습할 수 있는 옵션이 있다면(그러나 여전히 작은 장점만 있음) E는 강력한 PRP(SRP)입니다.게임 시작 전에 X에 대해 모든 q 값을 선택하는 경우(즉, 이전 쿼리에서 수집한 정보를 사용하여 각 X를 선택하지 않음) 상대는 비적응적입니다.

이러한 정의는 다양한 작동 모드를 분석하는 데 유용한 것으로 입증되었습니다.예를 들어 블록 암호 기반 암호화 알고리즘의 보안을 측정하는 유사한 게임을 정의한 후 (리덕션 인수를 통해) 이 새로운 게임에서 상대가 승리할 확률이 일부 A에 대해 P(A)보다_E 크지 않음을 보여줄 수 있습니다(리덕션은 일반적으로 A의 q와 실행 시간에 대한 제한을 제공합니다).마찬가지로 모든 관련 A에 대해 P(A)가 작을 경우_E 새로운 게임에서 승리할 수 있는 공격자는 많지 않다.이것에 의해, 상위 레벨의 알고리즘이 블록 암호의 시큐러티를 계승한다고 하는 생각이 공식화됩니다.

인 암호

평가

블록 암호는 실제로 여러 기준에 따라 평가할 수 있습니다.일반적인 요인은 다음과 같습니다.^[36]^[37]

키 크기 및 블록 크기 등의 키 파라미터는 둘 다 암호 보안의 상한을 제공합니다.
블록 암호 설계가 오랜 시간 동안 암호 해독에 큰 노력을 기울인 후 얻은 신뢰도, 설계의 수학적 건전성, 실용적 또는^[38] 인증적 공격의 존재에 기초한 추정 보안 수준입니다.
암호의 복잡성과 하드웨어 또는 소프트웨어 구현에 대한 적합성.하드웨어 구현은 게이트 수 또는 에너지 소비 측면에서 복잡성을 측정할 수 있으며, 이는 자원이 제한된 장치의 중요한 파라미터입니다.
메모리 요건을 포함한 다양한 플랫폼에서의 처리 스루풋에 관한 암호의 퍼포먼스.
암호 비용. 지적 재산권으로 인해 적용될 수 있는 라이센스 요건을 나타냅니다.
암호의 유연성. 여기에는 여러 키 크기 및 블록 길이를 지원하는 기능이 포함됩니다.

주목할 만한 블록 암호

루시퍼 / DES

루시퍼는 일반적으로 1970년대 IBM에서 Horst Feistel의 작업을 기반으로 개발된 최초의 민간 블록 암호로 간주됩니다.이 알고리즘의 개정 버전은 미국 정부 연방 정보 처리 표준 FIPS PUB 46 Data Encryption Standard(DES)^[39]로 채택되었습니다.미국 국립표준국(NBS)은 NBS(National Bureau of Standards, National Bureau of Standards, NBS)의 제출 및 내부 변경에 대한 공개 초청을 받아 선정하였다.DES는 1976년에 공개되어 널리 ^{[citation needed]}사용되고 있습니다.

DES는 특히 NSA에 의해 알려진 특정 암호 해독 공격에 저항하도록 설계되었으며 IBM에 의해 재발견되었지만 1980년대 후반 Eli Biham과 Adi Shamir에 의해 재발견될 때까지 공개적으로 알려지지 않았습니다.이 기술은 차분 암호 분석이라고 불리며 블록 암호에 대한 몇 안 되는 일반적인 공격 중 하나입니다. 선형 암호 분석은 또 다른 방법이지만, Mitsuru Matsui에 의해 발표되기 전에는 NSA에도 알려지지 않았을 수 있습니다.DES는 오픈 커뮤니티에서 암호화 및 암호 해석에 관한 많은 다른 작업과 출판물을 촉진했고, 많은 새로운 암호 ^{[citation needed]}설계에 영감을 주었습니다.

DES의 블록사이즈는 64비트, 키사이즈는 56비트입니다.64비트 블록은 DES 이후 블록 암호 설계에서 일반화되었습니다.키 길이는 정부 규제를 포함한 여러 요소에 따라 달라집니다.1970년대의 많은 관측자는^[who?] DES에 사용되는 56비트 키의 길이가 너무 짧다고 지적했습니다.시간이 지남에 따라, 특히 1998년 Electronic Frontier Foundation에 의해 DES를 파괴하도록 설계된 특수 목적 기계가 시연된 후, 그 부족함이 명백해졌습니다.DES, Triple DES, 3개의 독립 키(112비트 키 및 80비트 보안) 또는 3개의 독립 키(168비트 키 및 112비트 보안)를 사용하여 각 블록을 3중 암호화합니다.그것은 대체품으로 널리 채택되었다.미국 국립표준기술연구소(NIST) 표준에서는 80비트 보안 ^[40]수준 때문에 새로운 애플리케이션에서 2키 버전을 사용할 수 없게 되었지만 2011년 현재도 3키 버전은 여전히 안전한 것으로 간주되고 있습니다.

아이디어

International Data Encryption Algorithm(IDEA; 국제 데이터 암호화 알고리즘)은 ETH Zurich와 Xuejia Lai의 James Massey가 설계한 블록 암호로 1991년에 DES를 대체하기 위해 처음 설명되었습니다.

IDEA는 128비트키를 사용하는 64비트블록으로 동작하며 일련의 동일한 변환(1라운드)과 출력 변환(하프라운드)으로 구성됩니다.암호화와 복호화 프로세스는 비슷합니다.IDEA는 모듈러 덧셈과 곱셈, 비트 배타적(XOR) 등 여러 그룹에서 작업을 인터리브함으로써 보안의 대부분을 얻습니다.이들 그룹은 어떤 의미에서 대수적으로 "호환성이 없다"고 할 수 있습니다.

설계자는 IDEA를 분석하여 차분 암호해석에 대한 강도를 측정했으며 특정 가정 하에서 면역성이 있다는 결론을 내렸습니다.성공적인 선형 또는 대수적 약점은 보고되지 않았습니다.2012년 현재^[update] 모든 키에 적용되는 최고의 공격은 좁은 바이크 공격을 통해 전체 8.5라운드 IDEA를 무력 공격보다 약 4배속도는 무차별 공격보다 약 4배입니다.

RC5

RC5 블록 암호의 1라운드(2개의 하프라운드)

RC5는 1994년에 Ronald Rivest에 의해 설계된 블록 암호로, 다른 많은 암호와 달리 가변 블록 크기(32, 64 또는 128비트), 키 크기(0 ~2040비트) 및 라운드 수(0 ~255)를 가집니다.처음에 권장되었던 파라미터는 64비트 블록사이즈, 128비트키 및 12라운드였습니다.

RC5의 주요 특징 중 하나는 데이터 의존형 순환을 사용하는 것입니다. RC5의 목표 중 하나는 암호화 프리미티브로서 이러한 운영의 연구와 평가를 촉진하는 것입니다.또한 RC5는 다수의 모듈러 추가 및 XOR로 구성됩니다.알고리즘의 일반적인 구조는 Feistel과 같은 네트워크입니다.암호화 및 복호화 루틴은 몇 줄의 코드로 지정할 수 있습니다.그러나 주요 일정은 더 복잡하며, "nothing up my sleeve number"의 소스로 e와 황금 비율의 바이너리 확장과 함께 기본적으로 단방향 함수를 사용하여 키를 확장합니다.알고리즘의 심플함과 데이터 의존 회전의 참신함으로 인해 RC5는 암호 분석가들에게 매력적인 연구 대상이 되었습니다.

12-라운드 RC5(64비트블록 포함)는 2개의 선택된 플레인텍스트를 ^[41]사용하여⁴⁴ 차분 공격을 받기 쉽습니다.18~20라운드는 충분한 보호로 권장된다.

Rijndael / AES

벨기에의 암호학자 Joan Daemen과 Vincent Rijmen이 개발한 Rijndael 암호는 DES를 대체하는 경쟁 설계 중 하나였다.AES(Advanced Encryption Standard)가 되기 위한 5년간의 공모전에서 우승했습니다.

2001년에 NIST에 의해 채택된 AES의 고정 블록사이즈는 128비트, 키사이즈는 128비트, 키사이즈는 128비트, Rijndael은 32비트의 배수로 지정할 수 있습니다.블록 사이즈는 최대 256비트이지만 이론상 최대값은 없습니다.AES는 스테이트라고 불리는 4×4 줄의 바이트 순서 매트릭스에서 동작합니다(블록 사이즈가 큰 Rijndael 버전에는 스테이트에 추가 컬럼이 있습니다).

복어

Blowfish는 1993년 Bruce Schneier가 설계한 블록 암호로 다수의 암호 스위트 및 암호화 제품에 포함되어 있습니다.복어는 64비트 블록사이즈와 1비트부터 ^[42]448비트까지의 가변키 길이를 가지고 있습니다.16라운드 Feistel 암호로 키 의존성이 큰S 박스를 사용합니다.이 설계의 주목할 만한 특징으로는 키에 의존하는 S박스 및 매우 복잡한 키 스케줄이 있습니다.

이것은 노화 DES의 대안으로 다른 알고리즘과 관련된 문제와 제약이 없는 범용 알고리즘으로 설계되었다.Blowfish가 출시되었을 때, 다른 많은 디자인들은 특허에 의해 방해받거나 상업/정부 기밀이었다.슈나이어는 "복어는 특허가 없으며 모든 나라에서 그럴 것이다.이것에 의해, 이 알고리즘은 퍼블릭 도메인에 배치되어 누구나 자유롭게 사용할 수 있습니다.」Schneier의 후속 알고리즘인 Twofish도 마찬가지다.

일반화

조정 가능한 블록 암호

M. 리스코프, R. 리베스트, D.Wagner는 "tweakable" 블록 ^[43]암호라고 불리는 블록 암호의 일반화된 버전을 설명했습니다.조정 가능한 블록 암호는 일반적인 평문 또는 암호문 입력과 함께 조정이라고 불리는 두 번째 입력을 받아들입니다.tweak는 키와 함께 암호에 의해 계산된 치환을 선택합니다.변경 내용이 충분히 가볍다면(보통 상당히 비싼 키 설정 작업에 비해), 몇 가지 흥미로운 새로운 작동 모드가 가능해집니다.디스크 암호화 이론 문서에서는 이러한 모드에 대해 설명합니다.

포맷 보존 암호화

블록 암호는 전통적으로 바이너리 알파벳으로 작동합니다.즉, 입력과 출력 모두 n개의 0과 1로 구성된 이진 문자열입니다.단, 상황에 따라서는 다른 알파벳 상에서 동작하는 블록암호가 필요할 수 있습니다.예를 들어 16자리 신용카드 번호를 암호화하면 암호화 레이어를 레거시소프트웨어에 추가할 수 있습니다.다음 예에서는 형식을 유지하는 암호화를 보여 줍니다.보다 일반적으로 형식을 유지하는 암호화에는 일부 유한한 언어에서 키 있는 치환 기능이 필요합니다.이것에 의해, 포맷 보존 암호화 스킴은, 블록 암호(트레이킹 가능한)의 자연스러운 일반화가 됩니다.반면 CBC와 같은 기존 암호화 방식은 같은 평문이 고정 키를 사용하는 경우에도 여러 개의 다른 암호 텍스트로 암호화할 수 있기 때문에 순열이 아닙니다.

다른 암호화 프리미티브와의 관계

블록 암호는 다음과 같은 다른 암호화 프리미티브를 구축하는 데 사용할 수 있습니다.이러한 다른 기본 요소들이 암호화로 안전하게 보호되려면 올바른 방식으로 구축하도록 주의를 기울여야 합니다.

스트림 암호는 블록 암호를 사용하여 구축할 수 있습니다.OFB 모드 및 CTR 모드는 블록 암호를 스트림 암호로 변환하는 블록 모드입니다.
블록 ^[44]^[45]암호를 사용하여 암호화 해시 함수를 구축할 수 있습니다.이러한 방법에 대한 설명은 단방향 압축 함수를 참조하십시오.방식은 보통 암호화에 사용되는 블록 암호 모드와 유사합니다.
블록 ^[46]^[47]암호를 사용하여 암호학적으로 안전한 의사 난수 생성기(CSPRNG)를 구축할 수 있습니다.
임의의 크기의 유한 집합의 안전한 의사 난수 배열은 블록 암호로 구성할 수 있습니다. "형식 보존 암호화"를 참조하십시오.
일반적으로 알려진 예측 불가능한 치환과 키 화이트닝을 조합하면 블록 암호(단일 키 이븐 만수르 암호 등)를 구축하기에 충분합니다.이벤 만수르 암호는 가능한 한 가장 간단한 보안 블록 ^[48]암호일 수 있습니다.
Message Authentication Code(MAC; 메시지 인증 코드)는 블록 암호에서 구축되는 경우가 많습니다.CBC-MAC, OMAC 및 PMAC가 그러한 MAC입니다.
인증된 암호화도 블록 암호로 구축됩니다.암호화와 MAC를 동시에 실행하는 것을 의미합니다.즉, 기밀성과 인증을 모두 제공하는 것입니다.CCM, EAX, GCM 및 OCB는 이러한 인증 암호화 모드입니다.

SHA-1 및 SHA-2가 SHACAL로 독립적으로 사용되는 블록 암호를 기반으로 하는 것처럼 블록 암호를 구축하기 위해 해시 함수를 사용할 수 있습니다.이러한 블록 암호의 예로는 BEAR 및 LION이 있습니다.

「」를 참조해 주세요.

레퍼런스

^ Cusick, Thomas W.; Stanica, Pantelimon (2009). Cryptographic Boolean functions and applications. Academic Press. pp. 158–159. ISBN 9780123748904.
^ Menezes, Alfred J.; van Oorschot, Paul C.; Vanstone, Scott A. (1996). "Chapter 7: Block Ciphers". Handbook of Applied Cryptography. CRC Press. ISBN 0-8493-8523-7. Archived from the original on 2021-02-03. Retrieved 2012-07-15.
^ Bellare, Mihir; Rogaway, Phillip (11 May 2005), Introduction to Modern Cryptography (Lecture notes), 제 3 장.
^ Chakraborty, D.; Rodriguez-Henriquez, F. (2008). "Block Cipher Modes of Operation from a Hardware Implementation Perspective". In Koç, Çetin K. (ed.). Cryptographic Engineering. Springer. p. 321. ISBN 9780387718163.
^ 메네제스, 반 우르쇼트 & 밴스톤 1996 섹션 7.2
^ Shannon, Claude (1949). "Communication Theory of Secrecy Systems" (PDF). Bell System Technical Journal. 28 (4): 656–715. doi:10.1002/j.1538-7305.1949.tb00928.x. Archived from the original (PDF) on 2007-06-05. Retrieved 2012-04-09.
^ van Tilborg, Henk C. A.; Jajodia, Sushil, eds. (2011). Encyclopedia of Cryptography and Security. Springer. ISBN 978-1-4419-5905-8., 페이지 455.
^ van Tilborg & Jajodia 2011, 페이지 1268.
^ Rupp, Martin (16 August 2019). "The Benefits of the Atalla Key Block". Utimaco. Archived from the original on 17 October 2020. Retrieved 10 September 2019.
^ Hamscher, Walter (1998). "Electronic Business without Fear: The Tristrata Security Architecture" (PDF). CiteSeerX 10.1.1.123.2371. Archived from the original (PDF) on 29 May 2005.^{[자체 인식 소스?]}
^ Stiennon, Richard (17 June 2014). "Key Management a Fast Growing Space". SecurityCurrent. IT-Harvest. Retrieved 21 August 2019.
^ Junod, Pascal & Canteaut, Anne (2011). Advanced Linear Cryptanalysis of Block and Stream Ciphers. IOS Press. p. 2. ISBN 9781607508441.
^ Keliher, Liam; et al. (2000). "Modeling Linear Characteristics of Substitution–Permutation Networks". In Hays, Howard; Carlisle, Adam (eds.). Selected areas in cryptography: 6th annual international workshop, SAC'99, Kingston, Ontario, Canada, August 9–10, 1999 : proceedings. Springer. p. 79. ISBN 9783540671855.
^ Baigneres, Thomas; Finiasz, Matthieu (2007). "Dial 'C' for Cipher". In Biham, Eli; Yousseff, Amr (eds.). Selected areas in cryptography: 13th international workshop, SAC 2006, Montreal, Canada, August 17–18, 2006 : revised selected papers. Springer. p. 77. ISBN 9783540744610.
^ Cusick, Thomas W.; Stanica, Pantelimon (2009). Cryptographic Boolean functions and applications. Academic Press. p. 164. ISBN 9780123748904.
^ Katz, Jonathan; Lindell, Yehuda (2008). Introduction to modern cryptography. CRC Press. p. 166. ISBN 9781584885511., 페이지 166–186.
^ Subhabrata Samajder (2017). Block Cipher Cryptanalysis: An Overview. Kolkata: Indian Statistical Institute. pp. 5/52.
^ ^a ^b Katz & Lindell 2008, 페이지 170-172.
^ Katz & Lindell 2008, 페이지 171
^ Aumasson, Jean-Philippe; Bernstein, Daniel J. (2012-09-18). "SipHash: a fast short-input PRF" (PDF): 5. {{cite journal}}:Cite 저널 요구 사항 journal=(도움말)
^ Menezes, Oorschot & Vanstone 1996, 228-230, 7장. sfn 오류: 대상 없음: CITREFMenesOurschotVanstone 1996(도움말)
^ "Block Cipher Modes". NIST Computer Security Resource Center. 4 January 2017.
^ Meneses, van Oorschot & Vanstone 1996, 페이지 228-233.
^ ^a ^b Morris Dworkin (December 2001), "Recommendation for Block Cipher Modes of Operation – Methods and Techniques" (PDF), Special Publication 800-38A, National Institute of Standards and Technology (NIST), doi:10.6028/NIST.SP.800-38A
^ "Kryptographische Verfahren: Empfehlungen und Schlüssellängen", Bsi Tr-02102 (Technische Richtlinie) (Version 1.0), June 20, 2008
^ "ISO/IEC 10116:2006 Information technology — Security techniques — Modes of operation for an n-bit block cipher".
^ Bellare & Rogaway 2005, 페이지 101, 섹션 5.3.
^ Bellare & Rogaway 2005, 섹션 5.6.
^ ^a ^b Serge Vaudenay (2002). "Security Flaws Induced by CBC Padding Applications to SSL, IPSEC, WTLS...". Advances in Cryptology – EUROCRYPT 2002, Proc. International Conference on the Theory and Applications of Cryptographic Techniques. Springer Verlag (2332): 534–545.
^ ^a ^b Kenneth G. Paterson; Gaven J. Watson (2008). "Immunising CBC Mode Against Padding Oracle Attacks: A Formal Security Treatment". Security and Cryptography for Networks – SCN 2008, Lecture Notes in Computer Science. Springer Verlag (5229): 340–357.
^ ISO/IEC 9797-1: Information technology – Security techniques – Message Authentication Codes (MACs) – Part 1: Mechanisms using a block cipher, ISO/IEC, 2011
^ Martin, Keith M. (2012). Everyday Cryptography: Fundamental Principles and Applications. Oxford University Press. p. 114. ISBN 9780199695591.
^ Paar, Christof; et al. (2010). Understanding Cryptography: A Textbook for Students and Practitioners. Springer. p. 30. ISBN 9783642041006.
^ Matsui, Mitsuru. "Linear Cryptanalysis of DES Cipher". Mitsubishi Electric Corporation. 1 (3): 43 – via Computer & Information Systems Laboratory.
^ Matsui, M. & Yamagishi, A. "A new method for known plaintext attack of FEAL cipher". Advances in Cryptology – EUROCRYPT 1992.
^ 메네제스, 판 우르쇼트 & 밴스톤 1996, 페이지 227
^ James Nechvatal; Elaine Barker; Lawrence Bassham; William Burr; Morris Dworkin; James Foti; Edward Roback (October 2000), Report on the Development of the Advanced Encryption Standard (AES) (PDF), National Institute of Standards and Technology (NIST)
^ 암호는 애드버타이즈된 대로 동작하지 않는 것을 나타내는 공격(즉, 암호를 해독하는 데 관련된 난이도가 주장된 것보다 낮다)은 복잡성이 높기 때문에 실질적으로 달성할 수 없습니다.
^ FIPS PUB 46-3 Data Encryption Standard(DES; 데이터 암호화 규격)(1999년 제3판, 단, 예비 섹션 12에 이력 정보가 포함되어 있습니다)
^ 키 관리를 위한 NIST 스페셜 퍼블리케이션 800-57 권장 - Part 1: General (개정), 2007년 3월 2014년 6월 6일 Wayback Machine에서 아카이브
^ Biryukov A.와 Kushilevitz E.(1998).RC5의 암호 분석 개선. EUROCRYPT 1998.
^ Bruce Schneier (1993). "Description of a New Variable-Length Key, 64-Bit Block Cipher (Blowfish)". {{cite journal}}:Cite 저널 요구 사항 journal=(도움말)
^ Liskov, M.; Rivest, R.; Wagner, D. "Tweakable Block Ciphers" (PDF). Crypto 2002.
^ "ISO/IEC 10118-2:2010 Information technology — Security techniques — Hash-functions — Part 2: Hash-functions using an n-bit block cipher".
^ Menezes, van Oorschot 및 Vanstone 1996, 제9장: 해시함수와 데이터 무결성
^ Barker, E. B.; Kelsey, J. M. (2012). "NIST Special Publication 800-90A Recommendation for Random Number Generation Using Deterministic Random Bit Generators" (PDF). doi:10.6028/NIST.SP.800-90A. {{cite journal}}:Cite 저널 요구 사항 journal=(도움말)
^ Menezes, van Oorschot & Vanstone 1996, 제5장: 의사랜덤 비트와 시퀀스.
^ Orr Dunkelman, Nathan Keller, Adi Shamir.암호학의 미니멀리즘: 이븐-만수르 계획이 다시 찾아왔다.

추가 정보

Knudsen, Lars R.; Robshaw, Matthew (2011). The Block Cipher Companion. Springer. ISBN 9783642173417.

외부 링크

다수의 대칭 알고리즘의 리스트이며, 그 대부분은 블록 암호입니다.
블록 암호 라운지
블록 암호란 무엇입니까? RSA FAQ에서 확인
Gold Sequence 및 무질서한 로지스틱 텐트 시스템에 기반한 블록 암호

[1] Cusick, Thomas W.; Stanica, Pantelimon (2009). Cryptographic Boolean functions and applications. Academic Press. pp. 158–159. ISBN 9780123748904.

[HAC-2] Menezes, Alfred J.; van Oorschot, Paul C.; Vanstone, Scott A. (1996). "Chapter 7: Block Ciphers". Handbook of Applied Cryptography. CRC Press. ISBN 0-8493-8523-7. Archived from the original on 2021-02-03. Retrieved 2012-07-15.

[modern-crypto-3] Bellare, Mihir; Rogaway, Phillip (11 May 2005), Introduction to Modern Cryptography (Lecture notes), 제 3 장.

[4] Chakraborty, D.; Rodriguez-Henriquez, F. (2008). "Block Cipher Modes of Operation from a Hardware Implementation Perspective". In Koç, Çetin K. (ed.). Cryptographic Engineering. Springer. p. 321. ISBN 9780387718163.

[FOOTNOTEMenezesvan_OorschotVanstone1996section_7.2-5] 메네제스, 반 우르쇼트 & 밴스톤 1996 섹션 7.2

[shannon-6] Shannon, Claude (1949). "Communication Theory of Secrecy Systems" (PDF). Bell System Technical Journal. 28 (4): 656–715. doi:10.1002/j.1538-7305.1949.tb00928.x. Archived from the original (PDF) on 2007-06-05. Retrieved 2012-04-09.

[tilborg-7] van Tilborg, Henk C. A.; Jajodia, Sushil, eds. (2011). Encyclopedia of Cryptography and Security. Springer. ISBN 978-1-4419-5905-8., 페이지 455.

[FOOTNOTEvan_TilborgJajodia20111268-8] van Tilborg & Jajodia 2011, 페이지 1268.

[9] Rupp, Martin (16 August 2019). "The Benefits of the Atalla Key Block". Utimaco. Archived from the original on 17 October 2020. Retrieved 10 September 2019.

[10] Hamscher, Walter (1998). "Electronic Business without Fear: The Tristrata Security Architecture" (PDF). CiteSeerX 10.1.1.123.2371. Archived from the original (PDF) on 29 May 2005.^{[자체 인식 소스?]}

[Stiennon-11] Stiennon, Richard (17 June 2014). "Key Management a Fast Growing Space". SecurityCurrent. IT-Harvest. Retrieved 21 August 2019.

[12] Junod, Pascal & Canteaut, Anne (2011). Advanced Linear Cryptanalysis of Block and Stream Ciphers. IOS Press. p. 2. ISBN 9781607508441.

[13] Keliher, Liam; et al. (2000). "Modeling Linear Characteristics of Substitution–Permutation Networks". In Hays, Howard; Carlisle, Adam (eds.). Selected areas in cryptography: 6th annual international workshop, SAC'99, Kingston, Ontario, Canada, August 9–10, 1999 : proceedings. Springer. p. 79. ISBN 9783540671855.

[14] Baigneres, Thomas; Finiasz, Matthieu (2007). "Dial 'C' for Cipher". In Biham, Eli; Yousseff, Amr (eds.). Selected areas in cryptography: 13th international workshop, SAC 2006, Montreal, Canada, August 17–18, 2006 : revised selected papers. Springer. p. 77. ISBN 9783540744610.

[15] Cusick, Thomas W.; Stanica, Pantelimon (2009). Cryptographic Boolean functions and applications. Academic Press. p. 164. ISBN 9780123748904.

[16] Katz, Jonathan; Lindell, Yehuda (2008). Introduction to modern cryptography. CRC Press. p. 166. ISBN 9781584885511., 페이지 166–186.

[17] Subhabrata Samajder (2017). Block Cipher Cryptanalysis: An Overview. Kolkata: Indian Statistical Institute. pp. 5/52.

[FOOTNOTEKatzLindell2008170–172-18] Katz & Lindell 2008, 페이지 170-172.

[FOOTNOTEKatzLindell2008171-19] Katz & Lindell 2008, 페이지 171

[20] Aumasson, Jean-Philippe; Bernstein, Daniel J. (2012-09-18). "SipHash: a fast short-input PRF" (PDF): 5. {{cite journal}}:Cite 저널 요구 사항 journal=(도움말)

[FOOTNOTEMenezesOorschotVanstone1996228–230Chapter_7-21] Menezes, Oorschot & Vanstone 1996, 228-230, 7장. sfn 오류: 대상 없음: CITREFMenesOurschotVanstone 1996(도움말)

[NIST-modes-22] "Block Cipher Modes". NIST Computer Security Resource Center. 4 January 2017.

[FOOTNOTEMenezesvan_OorschotVanstone1996228–233-23] Meneses, van Oorschot & Vanstone 1996, 페이지 228-233.

[nist800-38a-24] Morris Dworkin (December 2001), "Recommendation for Block Cipher Modes of Operation – Methods and Techniques" (PDF), Special Publication 800-38A, National Institute of Standards and Technology (NIST), doi:10.6028/NIST.SP.800-38A

[BSI-rec-25] "Kryptographische Verfahren: Empfehlungen und Schlüssellängen", Bsi Tr-02102 (Technische Richtlinie) (Version 1.0), June 20, 2008

[26] "ISO/IEC 10116:2006 Information technology — Security techniques — Modes of operation for an n-bit block cipher".

[FOOTNOTEBellareRogaway2005101section_5.3-27] Bellare & Rogaway 2005, 페이지 101, 섹션 5.3.

[FOOTNOTEBellareRogaway2005section_5.6-28] Bellare & Rogaway 2005, 섹션 5.6.

[padding-attack-29] Serge Vaudenay (2002). "Security Flaws Induced by CBC Padding Applications to SSL, IPSEC, WTLS...". Advances in Cryptology – EUROCRYPT 2002, Proc. International Conference on the Theory and Applications of Cryptographic Techniques. Springer Verlag (2332): 534–545.

[oz-pad-30] Kenneth G. Paterson; Gaven J. Watson (2008). "Immunising CBC Mode Against Padding Oracle Attacks: A Formal Security Treatment". Security and Cryptography for Networks – SCN 2008, Lecture Notes in Computer Science. Springer Verlag (5229): 340–357.

[iso-iec_9797-1-31] ISO/IEC 9797-1: Information technology – Security techniques – Message Authentication Codes (MACs) – Part 1: Mechanisms using a block cipher, ISO/IEC, 2011

[32] Martin, Keith M. (2012). Everyday Cryptography: Fundamental Principles and Applications. Oxford University Press. p. 114. ISBN 9780199695591.

[33] Paar, Christof; et al. (2010). Understanding Cryptography: A Textbook for Students and Practitioners. Springer. p. 30. ISBN 9783642041006.

[34] Matsui, Mitsuru. "Linear Cryptanalysis of DES Cipher". Mitsubishi Electric Corporation. 1 (3): 43 – via Computer & Information Systems Laboratory.

[FEAL_linear-35] Matsui, M. & Yamagishi, A. "A new method for known plaintext attack of FEAL cipher". Advances in Cryptology – EUROCRYPT 1992.

[FOOTNOTEMenezesvan_OorschotVanstone1996227-36] 메네제스, 판 우르쇼트 & 밴스톤 1996, 페이지 227

[AESr2report-37] James Nechvatal; Elaine Barker; Lawrence Bassham; William Burr; Morris Dworkin; James Foti; Edward Roback (October 2000), Report on the Development of the Advanced Encryption Standard (AES) (PDF), National Institute of Standards and Technology (NIST)

[38] 암호는 애드버타이즈된 대로 동작하지 않는 것을 나타내는 공격(즉, 암호를 해독하는 데 관련된 난이도가 주장된 것보다 낮다)은 복잡성이 높기 때문에 실질적으로 달성할 수 없습니다.

[39] FIPS PUB 46-3 Data Encryption Standard(DES; 데이터 암호화 규격)(1999년 제3판, 단, 예비 섹션 12에 이력 정보가 포함되어 있습니다)

[NIST_SP_800-57-40] 키 관리를 위한 NIST 스페셜 퍼블리케이션 800-57 권장 - Part 1: General (개정), 2007년 3월 2014년 6월 6일 Wayback Machine에서 아카이브

[Biryukov-41] Biryukov A.와 Kushilevitz E.(1998).RC5의 암호 분석 개선. EUROCRYPT 1998.

[blowfish-paper-42] Bruce Schneier (1993). "Description of a New Variable-Length Key, 64-Bit Block Cipher (Blowfish)". {{cite journal}}:Cite 저널 요구 사항 journal=(도움말)

[tweak-43] Liskov, M.; Rivest, R.; Wagner, D. "Tweakable Block Ciphers" (PDF). Crypto 2002.

[44] "ISO/IEC 10118-2:2010 Information technology — Security techniques — Hash-functions — Part 2: Hash-functions using an n-bit block cipher".

[FOOTNOTEMenezesvan_OorschotVanstone1996Chapter_9:_Hash_Functions_and_Data_Integrity-45] Menezes, van Oorschot 및 Vanstone 1996, 제9장: 해시함수와 데이터 무결성

[46] Barker, E. B.; Kelsey, J. M. (2012). "NIST Special Publication 800-90A Recommendation for Random Number Generation Using Deterministic Random Bit Generators" (PDF). doi:10.6028/NIST.SP.800-90A. {{cite journal}}:Cite 저널 요구 사항 journal=(도움말)

[FOOTNOTEMenezesvan_OorschotVanstone1996Chapter_5:_Pseudorandom_Bits_and_Sequences-47] Menezes, van Oorschot & Vanstone 1996, 제5장: 의사랜덤 비트와 시퀀스.

[DKS-48] Orr Dunkelman, Nathan Keller, Adi Shamir.암호학의 미니멀리즘: 이븐-만수르 계획이 다시 찾아왔다.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[24]

[25]

[26]

[22]

[23]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[39]

[40]

[41]

[42]

[43]

[44]

[45]

[46]

[47]

[48]

Search

블록 암호

네임스페이스

더

목차

정의.

역사

설계.

반복된 블록 암호

대체 - 주변 네트워크

페이스텔 암호

라이-매시 암호

운용

ARX(추가 회전 X)또는)

기타 작업

동작 모드

패딩

암호 분석

무차별 공격

암호

암호

(보안)

★★★★★

인 암호

평가

주목할 만한 블록 암호

루시퍼 / DES

아이디어

RC5

Rijndael / AES

복어

일반화

조정 가능한 블록 암호

포맷 보존 암호화

다른 암호화 프리미티브와의 관계

「」를 참조해 주세요.

레퍼런스

추가 정보

외부 링크

Search

블록 암호

정의.

역사

설계.

반복된 블록 암호

대체 - 주변 네트워크

페이스텔 암호

라이-매시 암호

운용

ARX(추가 회전 X)또는)

기타 작업

동작 모드

패딩

암호 분석

무차별 공격

암호

암호

(보안)

★★★★★

인 암호

평가

주목할 만한 블록 암호

루시퍼 / DES

아이디어

RC5

Rijndael / AES

복어

일반화

조정 가능한 블록 암호

포맷 보존 암호화

다른 암호화 프리미티브와의 관계

「 」를 참조해 주세요.

레퍼런스

추가 정보

외부 링크

「」를 참조해 주세요.