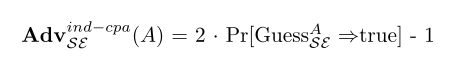암호문 구분 불가능

암호문을 구별할 수 없는 것은 많은 암호화 체계의 속성이다.직관적으로, 암호 시스템이 식별 불가능한 속성을 가지고 있다면, 적수는 암호화된 메시지에 기초하여 암호문 쌍을 구별할 수 없을 것이다.일부 체계는 또한 선택된 암호문 공격과 적응적으로 선택된 암호문 공격에 따라 구별할 수 없는 특성을 제공하지만, 선택한 일반 텍스트 공격에서 구별할 수 없는 특성을 대부분의 입증 가능한 보안 공개 키 암호 시스템에 대한 기본 요구사항으로 간주된다.선택된 평문 공격에 의한 식별 불가능성은 의미 보안의 속성과 동등하며, 많은 암호 증명들이 이러한 정의를 서로 교환하여 사용한다.

적에 의해 결정된 2개의 요소 메시지 공간에서 무작위로 선택한 메시지의 암호화를 고려할 때, 적에 의해 결정된 2개의 요소 메시지 공간에서 무작위적으로 선택된 메시지를 무작위 추측보다 훨씬 나은 확률로 메시지 선택을 식별할 수 없는 경우, 암호체계는 식별 불가능성의 측면에서 안전한 것으로 간주된다.½). 만일 어떤 적수가 1⁄2보다 유의하게 큰 확률로 선택된 암호문을 구별하는 데 성공할 수 있다면, 이 적수는 암호문을 구분하는 데 있어서 "장점"을 갖는 것으로 간주되며, 그 계획은 식별하기 어려운 측면에서 안전하다고 여겨지지 않는다.이 정의는 보안 체계에서 적수는 암호문을 보고 어떤 정보도 배우지 않아야 한다는 개념을 포함한다.따라서 상대는 무작위로 추측했을 때보다 더 잘할 수 있어야 한다.

형식 정의

불가분성의 관점에서 보안은 공격자의 능력에 대해 만들어진 가정에 따라 많은 정의를 가지고 있다.그것은 보통 게임으로 제시되는데, 어떤 상대도 무작위로 추측해야 하는 상대보다 훨씬 큰 확률로 게임을 이길 수 없다면 암호 시스템이 안전하다고 간주된다.암호화에 사용되는 가장 일반적인 정의는 선택한 일반 텍스트 공격(약칭 IND-CPA), (비적응적) 선택된 암호 텍스트 공격(IND-CCA1)에서 구별할 수 없으며, 적응적으로 선택된 암호 텍스트 공격(IND-CCA2)에서 구별할 수 없다.후자의 정의 중 하나에 따른 보안은 이전 정의에 따른 보안을 내포한다. 즉, IND-CCA1 보안인 체계는 IND-CCA1 보안인 체계는 IND-CCA1과 IND-CPA 보안인 체계는 모두 IND-CCA2 보안인 체계는 IND-CCA1과 IN-CPA 보안이다.따라서, IND-CCA2는 보안의 세 가지 정의 중 가장 강하다.

선택한 텍스트 공격(IND-CPA)에서 구별할 수

확률론적 비대칭 키 암호화 알고리즘의 경우, 선택된 일반 텍스트 공격(IND-CPA)에 따른 식별 불가능성은 적과 도전자 사이의 다음 게임에 의해 정의된다.컴퓨터 보안에 기반한 계획의 경우, 적수는 확률론적 다항 시간 튜링 기계에 의해 모델링되며, 이는 게임을 완료하고 다항 시간 단계 내에서 추측을 출력해야 한다는 것을 의미한다.이 정의에서 E(PK, M)는 PK 키 아래 메시지 M의 암호화를 나타낸다.

도전자는 일부 보안 파라미터 k(예: 키 크기(비트))를 기반으로 키 쌍 PK, SK를 생성해 상대에게 PK를 공개한다.도전자는 SK를 보유하고 있다.
상대방은 다항적으로 경계된 암호화 또는 기타 작업을 수행할 수 있다.
결국, 적수는 두 개의 뚜렷한 선택된 일반 텍스트 $\scriptstyle M_{0},M_{1}$ $\scriptstyle M_{0},M_{1}$ M $\scriptstyle M_{0},M_{1}$ ${\$ 1}을 도전자에게 $\scriptstyle M_{0},M_{1}$ 제출한다.
도전자는 비트 b $∈{\$ 0, 1}를 임의로 선택하고 도전 암호문 C = E(PK, M $\scriptstyle M_{b}$ ${\$ 를 다시 적에게 보낸다 $\scriptstyle M_{b}$
상대방은 얼마든지 추가 계산이나 암호화를 자유롭게 수행할 수 있다.
마지막으로 상대방은 b의 값에 대한 추측을 출력한다.

모든 확률론적 다항식 시간 적수가 무작위 추측에 비해 무시할 수 있는 "장점"만 가지고 있는 경우, 선택한 일반 텍스트 공격에서는 암호 시스템을 구별할 수 없다.An adversary is said to have a negligible "advantage" if it wins the above game with probability $\scriptstyle \left({\frac {1}{2}}\right)\,+\,\epsilon (k)$ , where $\scriptstyle \epsilon (k)$ is a negligible function in the security parameter k, that is for every (noNzero)다항 함수 p o 나는 에스파냐의(){\displaystyle\scriptstyle poly()}관계가 k0{\displaystyle\scriptstyle k_{0}}가ϵ(k)<1p시 나는 에스파냐의(k){\displaystyle\scriptstyle \epsilon(k)\와 같이,<>\;\left{\frac{1}{poly(k)}}\right}에 대한 모든 k대리자 k 0{\displays.tyle \scr $iptstyle$ k $\;>\;k_{0$

적수는 $\scriptstyle M_{0}$ 0 ${\$ $\scriptstyle M_{1}$ $\scriptstyle M_{1}$ ${\$ PK를 $\scriptstyle M_{1}$ 알고 있지만, E의 확률론적 $\scriptstyle M_{b}$ 은 $\scriptstyle M_{b}$ b $\scriptstyle M_{b}$ {\ $displaystyle \scriptstyle M_{b}$ 의 암호화가 여러 유효한 암호문 중 하나에 불과함을 $\scriptstyle M_{b}$ $\scriptstyle M_{0}$ 하므로 M $\scriptstyle M_{0}$ {\ $discryption$ } $스타일 \scriptstyle M_{0$ $\scriptstyle M_{1}$ 1 ${\$ 및 $\scriptstyle M_{1}$ 결과적인 암호문을 챌린지 암호문과 비교하는 것은 적에게 불가결한 이점을 제공하지 않는다.

위의 정의는 비대칭 키 암호체계로 한정되어 있지만, 공개키 암호화 기능을 암호화 오라클로 대체하여 대칭 케이스에 적응할 수 있는데, 이 암호키를 유지하고 상대방의 요청에 따라 임의의 일반 텍스트를 암호화한다.

대칭 IND-CPA 게임, 공식화

선택된 일반 텍스트 공격을 수행하는 적대적 과정은 보통 암호화 게임의 형태로 윤곽이 잡힌다.대칭 IND-CPA를 테스트하기 위해 위에서 설명한 게임을 정의한다.^[1] ${\mathcal {K}}$ ${\$ $displaystyle {\mathcal {K}$ 을(를) 키 생성 함수로 ${\mathcal {E}}$ E ${\$ { $E}$ 을 ${\mathcal {E}}$ (를) 암호화 함수로 하고 D {\ $displaystyle {\$ mathcal { $D}$ 을(를) 암호 해독 함수로 한다 ${\mathcal {D}}$ .Let ${\mathcal {S}}{\mathcal {E}}=({\mathcal {K}},{\mathcal {E}},{\mathcal {D}})$ ${\mathcal {S}}{\mathcal {E}}=({\mathcal {K}},{\mathcal {E}},{\mathcal {D}})$ = ${\mathcal {S}}{\mathcal {E}}=({\mathcal {K}},{\mathcal {E}},{\mathcal {D}})$ ( ${\mathcal {S}}{\mathcal {E}}=({\mathcal {K}},{\mathcal {E}},{\mathcal {D}})$ , ${\mathcal {S}}{\mathcal {E}}=({\mathcal {K}},{\mathcal {E}},{\mathcal {D}})$ , ${\mathcal {S}}{\mathcal {E}}=({\mathcal {K}},{\mathcal {E}},{\mathcal {D}})$ ) ${\displaystyle {\mathcal{S}{\mathcal{E}=({\mathcal$ {K $},{\mathcal$ {E $},{\mathcal{D})}}}}$ 은 대칭 암호화 체계로 한다 ${\mathcal {S}}{\mathcal {E}}=({\mathcal {K}},{\mathcal {E}},{\mathcal {D}})$ . $G$ $u$ $e$ $s$ $Gamet$ 게임은 다음과 같이 정의된다 $Guess$ .

원하는 횟수만큼 적수는 자신이 선택한 두 개의 일반 텍스트 메시지를 선택하여 메시지 중 하나를 암호화하는 암호문을 반환하는 LR 오라클에 제공한다.상대의 장점은 LR 오라클에서 암호화된 메시지를 결정하는 게임 시작 시 무작위로 선택한 값인 b의 값을 추측할 확률에 의해 결정된다.따라서 그 장점은 다음과 같이 정의된다.^[1]

선택한 암호문 공격/적응형 선택 암호문 공격(IND-CCA1, IND-CCA2)에서 구별할 수 없음

비적응적이고 적응력이 뛰어난 선택 암호문 공격(IND-CCA1, IND-CCA2)에서는 IND-CPA와 유사한 정의를 사용한다.그러나, 공용 키(또는 대칭의 경우 암호화 오라클) 외에, 상대방은 상대방의 요청에 따라 임의의 암호문을 해독하는 암호 해독 오라클에 대한 액세스 권한을 부여받아 일반 텍스트를 반환한다.비적응적 정의에서 적수는 도전 암호문을 수신할 때까지만 이 신탁을 쿼리할 수 있다.적응형 정의에서 적수는 도전 암호문을 받은 후에도 해독용 암호문을 통과하지 못할 수 있다는 주의와 함께 해독 오라클에 대해 계속 질의할 수 있다(그렇지 않으면 정의는 사소한 것일 것이다).

도전자는 일부 보안 파라미터 k(예: 키 크기(비트))를 기반으로 키 쌍 PK, SK를 생성해 상대에게 PK를 공개한다.도전자는 SK를 보유하고 있다.
적수는 임의의 암호화, 임의의 암호문 기반 암호 해독 오라클에 대한 호출 또는 기타 연산을 수행할 수 있다.
결국, 적수는 두 개의 뚜렷한 선택된 일반 텍스트 $\scriptstyle M_{0},\,M_{1}$ $\scriptstyle M_{0},\,M_{1}$ M $\scriptstyle M_{0},\,M_{1}$ ${\$ }을 도전자에게 $\scriptstyle M_{0},\,M_{1}$ 제출한다.
도전자는 비트 b ∈{0, 1}를 무작위로 균일하게 선택하고, "챌린지" 암호문 C = E(PK, $\scriptstyle M_{b}$ $\scriptstyle M_{b}$ ${\$ 를 다시 적에게 보낸다.
상대방은 얼마든지 추가 계산이나 암호화를 자유롭게 수행할 수 있다.
1. 비적응 사례(IND-CCA1)에서 적수는 암호 해독 오라클로 더 이상 전화를 걸지 않을 수 있다.
2. 적응형 사례(IND-CCA2)에서 적수는 암호 해독 오라클로 추가 호출을 할 수 있지만 도전 암호문 C는 제출하지 않을 수 있다.
마지막으로 상대방은 b의 값에 대한 추측을 출력한다.

전술한 게임에서 이길 수 없는 이점이 있는 적이 없는 경우, 계획은 IND-CCA1/IND-CCA2 보안이다.

무작위 노이즈와 구별할 수 없음

때때로 우리는 암호문 문자열이 적에 의해 임의의 문자열과 구별되지 않는 암호화 체계가 필요하다.^[2]

만약 적수가 메시지가 존재하는지조차 알 수 없다면, 그것은 메시지를 쓴 사람에게 그럴듯한 경멸감을 준다.

암호화된 통신 링크를 구축하는 일부 사람들은 트래픽 분석을 더 어렵게 하기 위해 암호화된 각 데이터그램의 내용을 무작위 데이터와 구별할 수 없게 만드는 것을 선호한다.^[3]

암호화된 데이터를 저장하기 위해 시스템을 구축하는 일부 사람들은 데이터를 더 쉽게 숨기기 위해 데이터를 무작위 데이터와 구별하지 못하게 하는 것을 선호한다.예를 들어 TrueCrypt와 같은 일부 디스크 암호화는 일부 데이터 삭제에서 남겨진 무해한 무작위 데이터의 데이터를 숨기려고 시도한다.또 다른 예로, 일부 스테가노그래피는 디지털 사진의 순수한 "랜덤" 이미지 노이즈의 통계적 특성과 일치하도록 하여 데이터를 숨기려고 한다.

그러한 가칭적인 암호화 시스템을 지원하기 위해, 몇 가지 암호 알고리즘은 암호문 메시지를 무작위 비트 문자열과 구별할 수 없도록 특별히 설계되어 있다.^[4]^[5]^[6]

대부분의 애플리케이션은 무작위 비트와 구별할 수 없는 암호화된 메시지를 생성하기 위해 암호화 알고리즘을 필요로 하지 않는다.그러나 일부 저자들은 그러한 암호화 알고리즘을 개념적으로 더 단순하고 쉽게 사용할 수 있으며 실제로 보다 다재다능한 것으로 간주하고 있으며, 대부분의 IND-CPA 암호화 알고리즘은 사실상 무작위 비트와 구별할 수 없는 암호화된 메시지를 생성하는 것으로 보인다.^[7]

동등성 및 시사점

구별할 수 없는 것은 암호화된 통신의 기밀성을 유지하기 위한 중요한 재산이다.그러나 일부의 경우 구별할 수 없는 속성은 명백히 관련이 없는 다른 보안 속성을 암시하는 것으로 밝혀졌다.때로는 이러한 함축적 의미가 양방향으로 작용하여 두 가지 정의를 동등하게 만들기도 한다. 예를 들어, 적응적 선택 암호문 공격(IND-CCA2)에 따라 구별할 수 없는 특성의 특성이 동일한 공격 시나리오(NM-CCA2)에 따라 비말랄리티의 특성과 동일하다고 알려져 있다.비유해성은 기밀성이라기 보다는 메시지 무결성을 다루는 속성이기 때문에 이러한 동등성은 즉시 명백하지 않다.다른 경우에, 여전히 다른 유용한 정의를 암시하기 위해, 구별할 수 없는 것이 특정한 다른 정의와 결합될 수 있다는 것이 증명되었다.다음 목록은 비록 그것이 결코 완전한 것은 아니지만, 몇 가지 알려진 함의를 요약한다.

A $\scriptstyle A\;\Rightarrow \;B$ B ${\$ A $\;\Rightarrow \;B}$ 라는 표기법은 속성 A가 속성 B를 암시한다는 것을 의미한다 $\scriptstyle A\;\Rightarrow \;B$ . $\scriptstyle A\;\Leftrightarrow \;B$ $\scriptstyle A\;\Leftrightarrow \;B$ ${\$ 은 속성 A와 B가 동일하다는 것을 의미한다 $\scriptstyle A\;\Leftrightarrow \;B$ . $\scriptstyle A\;\not \Rightarrow \;B$ $\scriptstyle A\;\not \Rightarrow \;B$ ${\$ A $\;\not \Rightarrow \;B}$ 은 속성 A가 속성 B를 반드시 암시하는 것은 아님을 의미한다 $\scriptstyle A\;\not \Rightarrow \;B$ .

CPA 아래의 IND-CPA ⇔ ${\$ 의미 $\scriptstyle \Leftrightarrow$ 보안.
NM-CPA(선택한 일반 텍스트 공격 시 유해성이 없음) $\scriptstyle \Rightarrow$ ${\$ IND-CPA $\scriptstyle \Rightarrow$ .
NM-CPA(선택한 일반 텍스트 공격 시 유해성이 없음) $\scriptstyle \not \Rightarrow$ ${\$ IND-CCA2 $\scriptstyle \not \Rightarrow$ .
NM-CCA2(적응적으로 선택한 암호문 공격 시 악성코드가 아님) $\scriptstyle \Leftrightarrow$ ${\$ IND-CCA2 $\scriptstyle \Leftrightarrow$ .

참고 항목

참조

^ ^a ^b Bellare, Mihir; Rogaway, Phillip (May 11, 2005). "Introduction to Modern Cryptography, Chapter 5: Symmetric Encryption" (PDF). p. 93. Retrieved 6 April 2020.
^ Chakraborty, Debrup; Rodríguez-Henríquez., Francisco (2008). Çetin Kaya Koç (ed.). Cryptographic Engineering. p. 340. ISBN 9780387718170.
^ iang (2006-05-20). "Indistinguishable from random". Retrieved 2014-08-06.
^ Bernstein, Daniel J.; Hamburg, Mike; Krasnova, Anna; Lange, Tanja (2013-08-28). "Elligator: Elliptic-curve points indistinguishable from uniform random strings" (PDF). Retrieved 2015-01-23.
^ Möller, Bodo (2004). "A Public-Key Encryption Scheme with Pseudo-random Ciphertexts". Computer Security – ESORICS 2004. Lecture Notes in Computer Science. Vol. 3193. pp. 335–351. doi:10.1007/978-3-540-30108-0_21. ISBN 978-3-540-22987-2.
^ Moore, Cristopher; Mertens, Stephan (2011). The Nature of Computation. ISBN 9780191620805.
^ Rogaway, Phillip (2004-02-01). "Nonce-Based Symmetric Encryption" (PDF). pp. 5–6. Retrieved 2014-08-07.

Katz, Jonathan; Lindell, Yehuda (2007). Introduction to Modern Cryptography: Principles and Protocols. Chapman & Hall / CRC Press. ISBN 978-1584885511.

[:0-1] Bellare, Mihir; Rogaway, Phillip (May 11, 2005). "Introduction to Modern Cryptography, Chapter 5: Symmetric Encryption" (PDF). p. 93. Retrieved 6 April 2020.

[2] Chakraborty, Debrup; Rodríguez-Henríquez., Francisco (2008). Çetin Kaya Koç (ed.). Cryptographic Engineering. p. 340. ISBN 9780387718170.

[3] (2006-05-20). "Indistinguishable from random". Retrieved 2014-08-06.

[4] Bernstein, Daniel J.; Hamburg, Mike; Krasnova, Anna; Lange, Tanja (2013-08-28). "Elligator: Elliptic-curve points indistinguishable from uniform random strings" (PDF). Retrieved 2015-01-23.

[5] Möller, Bodo (2004). "A Public-Key Encryption Scheme with Pseudo-random Ciphertexts". Computer Security – ESORICS 2004. Lecture Notes in Computer Science. Vol. 3193. pp. 335–351. doi:10.1007/978-3-540-30108-0_21. ISBN 978-3-540-22987-2.

[6] Moore, Cristopher; Mertens, Stephan (2011). The Nature of Computation. ISBN 9780191620805.

[7] Rogaway, Phillip (2004-02-01). "Nonce-Based Symmetric Encryption" (PDF). pp. 5–6. Retrieved 2014-08-07.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

Search