시간/메모리/데이터 트레이드오프 공격
Time/memory/data tradeoff attack시간/메모리/데이터 트레이드오프 공격은 공격자가 시공간 트레이드오프와 유사한 상황을 달성하려고 하는 암호 공격의 한 유형으로, 공격자가 사용할 수 있는 데이터의 양을 나타내는 추가적인 데이터 매개 변수를 사용합니다.공격자는 이들 파라미터 중1개 또는 2개를 다른 파라미터에 유리하게 조정하거나 줄입니다.이런 유형의 공격은 매우 어렵기 때문에 사용 중인 대부분의 암호 및 암호화 방식은 이를 [citation needed]방지하도록 설계되지 않았습니다.
역사
대칭 암호 시스템에 대한 트레이드오프 공격은 1980년으로 거슬러 올라가며, Martin Hellman은 T N 2 \ 2 } = N 2 \ T tt t in in in in in in in in in in in in by by by by by by by by by by by by by by by by by by by by t t t t t t t t t t t t t t t t t t t t t t t t t t t t t t t t t t t t t t t t t t t t t t t t}={N^{2}}}1≤ T≤ N{1\leq T\leq N\displaystyle}.[1]후에, 1995년, 배비지와 Golic을 고안했다 다른 절충 공격에 대해 스트림 암호화와 새로운 바인딩 되는 것처럼 TM)N{TM=N\displaystyle}을 위해 1≤ T≤ D{1\leq T\leq D\displaystyle}이 D{D\displaystyle}출력 데이터 사용할 수 있cryp.황갈색실시간으로 [2][3]확인할 수 있습니다.
어택 메카니즘
이 공격은 일반적인 암호 분석 시간/메모리 트레이드오프 공격의 특별한 버전으로, 다음 2가지 주요 단계가 있습니다.
- 전처리:
이 단계에서 공격자는 암호 시스템의 구조를 탐색하고 검색 결과를 큰 테이블에 기록할 수 있습니다.이 작업은 시간이 오래 걸릴 수 있습니다. - 실시간:
이 단계에서 암호분석가는 특정 미지의 키로부터 얻은 실데이터를 부여받는다.그런 다음 이 데이터를 사전 처리 단계에서 미리 계산된 표와 함께 사용하여 가능한 한 짧은 시간 내에 특정 키를 찾으려 합니다.
시간/메모리/데이터 트레이드오프 공격에는 다음 파라미터가 있습니다.
- \N \ search space size
- 전처리단계에 소요된P\P
- 실시간 단계에 필요한 TT 시간
- 가 사용할 수 있는 메모리 양M})
- D의 실시간 데이터 양(공격자가 사용 가능)
블록 암호에 대한 헬먼의 공격
블록 암호의 경우 가능한 키의 총 개수는N {\N}으로 가능한 플레인 텍스트 및 암호 텍스트의 개수는N {\ N으로 가정합니다.또한 지정된 데이터는 특정 플레인 텍스트의 단일 암호 블록으로 합니다.에서 로의 매핑을 NN 포인트 에서 랜덤 치환 f f로 간주하고 이 f(\ f가 반전 가능한 경우 의 역수를 구해야 합니다 ) {\)= 이 함수를 반전시키는 Hellman의 기술:
- 전처리 단계 중
- 의 공간을m의의 시작점에서 의 를tt 반복하여 구성되는 ×t{ t의 직사각형 매트릭스로 커버합니다.시작점은 행렬에서 가장 왼쪽에 있는 열이고 끝점은 가장 오른쪽에 있는 열입니다.그런 다음 시작점과 끝점의 쌍을 끝점 값의 오름차순으로 저장합니다.
- 이제 하나의 매트릭스만 디스플레이 N 공간을 모두 커버할 수 없습니다.그러나 행렬에 행을 추가하면 복구된 점을 여러 번 포함하는 거대한 행렬이 생성됩니다.따라서 매트릭스에 서로 포인트가 의 임계값을 찾을 수 있습니다.시작점에서 끝점까지의 첫 m개의 \m개의 경로가 모두 의 mt개의 포인트와 되어 있으며 이전 경로 중 하나와 공통점을 하나 이상 가지며 t개의 \t포인트를 포함하는 다음 경로가 있다고 가정합니다.이 의 t mt와 t t는 t tmt\ N을 확인하면 생일 역설에 의해 분리됩니다.에 대해서는, m t t 2 (\m^{의 매트릭스 정지 룰을 적용합니다.
- 그러나 m {\m{2}=인m × {\ 은 전체 공간의 일부를 한다.공간 전체를 커버하는 tt를 하려면 {x) = { 의 정렬과 같이 정의된 f{}의 된 형식을 사용합니다 [1] (자세한 내용은 원본 문서를 참조하십시오).그리고 총 전처리 시간은 PN(\ P N을 알 수 있습니다.또한 시작점과 끝점의 쌍만 저장하면 되고m\m의 각 쌍에 이 존재하기 때문에 t(\ mt입니다.
- 실시간 단계 중
- f- ( ) { f^ { - ( ) }을(를) 데 필요한 총 계산은 T 2 ( \ T =^ } )입니다. 왜냐하면 하나의 매트릭스로 커버될 가능성이 높기 때문에 각 시도마다 f - (\ {\ t}ystyle 입니다.최적의 트레이드오프 곡선은 매트릭스 정지 N {\}^{ = N 、 1 {\ T} = { = {{DISPLAY} = D = 1= 1 of of of of of of of of of of of of of of of t t of of t t t t t t t t t t t t t t t t t t t t t t t t t t t t t t t t t t t t
Hellman에 따르면 블록 암호의 키에서 암호 텍스트로의 매핑이 N N 포인트 의 랜덤 치환 ff라는 특성이 있으며 이 f f가 반전 가능한 경우 트레이드오프 관계가 크게 개선됩니다. M { TM
스트림 암호에 대한 배비지 앤 골릭 공격
스트림 암호의 경우 N{\ N은 비트 제너레이터의 내부 상태 수로 지정되며, 키 수와 다를 수 있습니다.D)는 제너레이터에서 생성된 첫 번째 의사 난수 비트 수입니다.마지막으로 공격자는 비트 제너레이터의 실제 내부 상태 중 하나를 찾아 이 시점부터 제너레이터를 실행하여 나머지 키를 생성할 수 있도록 하는 것입니다.비트 제너레이터의 한N개(\N 내부 상태를 각각 상태에서 를 실행함으로써 얻은 번째 비트로 구성된 문자열에 연결합니다 f)=y 를 출력합니다.\ y를 출력합니다.이 이전 매핑은(\ N 포인트 공통 에서 랜덤 함수로 간주됩니다.공격자는 이 기능을 반전시키기 위해 다음을 설정합니다.
- 전처리 단계에서M {\ M x {\} states를 하고 하는 y{\ 출력 프레픽스를 계산합니다.
- , i){ {을 })의 순서로 큰 테이블에 저장합니다.
- 실시간 단계에서는 D+ g () - \ D + ( )-개의 비트가 됩니다. g { log(N)} {displaystyle log( {{ {의 한 (\ D의 조합을 계산합니다
- 생성된 테이블에서 로그 시간이 걸리는 각 i})를 검색합니다.
- 히트가 있는 경우 는 비트 제너레이터의 xi에 대응합니다.여기서 제너레이터를 포워드하여 나머지 키를 얻을 수 있습니다.
- 생일 패러독스에 따르면N(\displaystyle N의 이 N N보다 클 경우 공간의 두 서브셋이 교차하는 것을 보증합니다.
생일 공격의 결과로 공격 T {\ T 및 P M {\ P의 { DM을얻을 수 e 실시간으로 사용 가능한 데이터이며 T (\ T를 1(\1)로 수 있으며, 최종적으로는 일반 트레이드오프 곡선이 (\ TM이 되고 1 D(\ 1 P및 D (\d)가 된다.
샤미르와 비류코프의 암호 공격
2000년에 도입된 이 참신한 아이디어는 Hellman과 Babbage-and-Golic 트레이드오프 공격을 결합하여 스트림 암호 [4]분석을 위한 보다 나은 경계를 가진 새로운 트레이드오프 곡선을 달성합니다.Hellman의 블록 암호 기술은 내부 상태를 출력 프리픽스에 매핑하는 f f의 여러 에서 얻은 행렬을 통해 N N 포인트 을 커버하는 것과 동일한 아이디어를 사용하여 스트림 암호에 적용할 수 있습니다. 암호에 대한 이 트레이드오프 공격은 N N을 하는 매트릭스 중에서 D(\D) 출력 프레픽스가 발견되면 성공합니다.이것에 의해 N(\ N에서 N(\ N/ 포인트로 매트릭스별 커버 포인트 수가 됩니다.이는 m tdisplaystyle t}를 가능한 한 유지하면서 매트릭스 를t t로 줄임으로써 이루어집니다(단, 적어도1개의 테이블을 가지려면 t (\ t D가 합니다).이 새로운 공격에 대해서는 매트릭스 수를 t 스타일 M=로 전처리 PN PD를 동일하게 줄임으로써 /D( 스타일 P=D)가 . 공격에 필요한 실시간은 T D( T)입니다. D 매트릭스 수, 각 반복의 길이 및 공격 시 사용 가능한 데이터 포인트 수의 곱입니다.
결국 우리는 다시 매트릭스 정지 규칙을 사용하여 트레이드오프 µ ( / { TM D2} ^2} {를 구한다. D
샘플링 저항이 낮은 스트림 암호에 대한 공격
Biryukov, Shamir 및 Wagner에 의해 발명된 이 공격은 일부 스트림 암호의 특정 기능에 의존합니다.즉, 비트 제너레이터는 다음 출력 [5]비트를 생성하기 전에 내부 상태의 변화를 거의 겪지 않습니다.따라서 k k의 작은 값에 대해k{ k 제로비트를 하는 특수한 상태를 저비용으로 열거할 수 있습니다.그러나 다수의 출력 비트가 특정 값을 취하도록 강제할 경우 이 열거 프로세스는 매우 비용이 많이 들고 어려워집니다.이제 스트림 암호의 샘플링 저항은 -k {\ R =이고k {\ k는 열거를 가능하게 하는 최대값이다.
스트림 는 N N 상태 각각에 의 풀네임과 대응하는 출력 이름( 출력 시퀀스의 첫 번째 이 있다고 가정합니다.이 스트림 암호의 샘플링 R -k(\ R인 경우 효율적인 열거는 n-(\ 비트의 이름을 사용하여 제너레이터의 특수 상태를 정의할 수 있습니다.n- { style } 단축 이름을 각 특수 상태에는 n -k { style } 비트의 출력 이름이 있습니다. 이는 첫 k{ k 선두 비트를 제거한 후 특수 상태의 출력 시퀀스입니다.Now, we are able to define a new mapping over a reduced space of points and this mapping is equivalent to the original mapping. R1 ( \ DR \ 1 로 하면 공격자가 이용할 수 있는 실시간데이터는 이러한 특수상태의 출력을 적어도1개 가질 수 있습니다.그렇지 않으면 특수 상태의 정의를 완화하여 더 많은 포인트를 포함합니다.Shamir와 Biryukov의 새로운 시간/메모리/데이터 트레이드오프 공격에서 DR에 ( D)와 NDisplaystyle NR에 의한 N( N을 대체하면 동일한 트레이드오프 TM2)를 얻을 수 있다. R( style ( )^T\NR) 。은, ( style ( 의 사이즈를 11)까지 할 수 있기 때문에 실제로 T 1)의 하한을 완화할 수 있기 때문에, 개선한 것입니다. 기술을 사용하면 특수 스타일 포인트에만 액세스하므로 고가의 디스크 액세스 작업 수가 tR에서로 하며, 고가의 디스크 작업 수가 줄어들기 때문에 공격이 더욱 빨라집니다.
레퍼런스
- ^ a b Hellman, M.E., "암호 분석 타임 메모리 트레이드오프", 정보 이론, IEEE 트랜잭션 on, vol.26, no.4, 페이지 401,406, 1980년 7월
- ^ 배비지, S. H., "스트림 암호에 대한 "파괴적 검색" 공격 개선", 보안 및 검출, 1995., vol., no., pp.161-166, 1995년 5월 18일 유럽 협약
- ^ Golic, J. 컴퓨터 사이언스, 암호학의 진보에 관한 "A5 스트림 암호의 암호화" 강의 노트 - EUROCRYPT '97, LNCS 1233, 페이지 239-255, Springer-Verlag 1997
- ^ Biryukov A., Shamir A., "Stream Ciphers의 암호 분석 시간/메모리/데이터 트레이드오프" 컴퓨터 사이언스 강의 노트, 암호학의 진보 - ASIACRYPT 2000, LNCS 1976, pp.1-13, Springer-ver Berlag Berlin Heidelerg 2000
- ^ Biryukov A., Shamir A., Wagner D, "PC상의 A5/1 실시간 암호화" Fast Software Encryption 2000, 페이지 1-18, Springer-Verlag 2000




 실시간 데이터 양(공격자가 사용 가능)
실시간 데이터 양(공격자가 사용 가능)
 매핑을 N
매핑을 N 간주하고 이
간주하고 이 


 직사각형 매트릭스로 커버합니다.시작점은 행렬에서 가장 왼쪽에 있는 열이고 끝점은 가장 오른쪽에 있는 열입니다.그런 다음 시작점과 끝점의 쌍을 끝점 값의 오름차순으로 저장합니다.
직사각형 매트릭스로 커버합니다.시작점은 행렬에서 가장 왼쪽에 있는 열이고 끝점은 가장 오른쪽에 있는 열입니다.그런 다음 시작점과 끝점의 쌍을 끝점 값의 오름차순으로 저장합니다.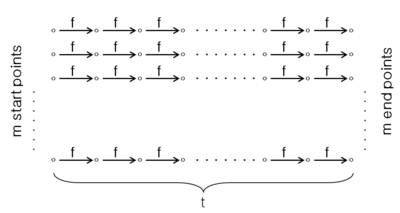



 전체 공간의 일부를
전체 공간의 일부를 





 . 왜냐하면
. 왜냐하면













 된다.
된다.
 줄임으로써 이루어집니다(단, 적어도1개의 테이블을 가지려면 t
줄임으로써 이루어집니다(단, 적어도1개의 테이블을 가지려면 t 



 작은 값에 대해
작은 값에 대해






 N
N
 사이즈를 1
사이즈를 1


