아르키메데스 재산
Archimedean property추상 대수학 및 분석에서 고대 그리스의 수학자인 시라큐스의 아르키메데스(Archimedes)의 이름을 딴 아르키메데스(Archimedes) 속성은 순서 또는 규범집단, 분야 등 일부 대수적 구조에 의해 보유되는 속성이다. 일반적으로 해석되는 속성은 두 개의 양수 x와 y가 주어진 경우 nx > y가 되도록 정수 n이 있다고 명시한다. 그것은 또한 자연수의 집합이 위에 경계되어 있지 않다는 것을 의미한다.[1] 대충 말하면 무한히 크거나 무한히 작은 원소가 없는 속성이다. 아르키메데스의 '구체와 원통 위에'의 'Axiom V'로 등장하기 때문에 아르키메데스의 공리를 붙인 것은 오토 스톨츠였다.[2]
그 개념은 고대 그리스의 규모론에서 비롯되었다; 그것은 여전히 데이비드 힐버트의 기하학 공리와 같은 현대 수학에서 중요한 역할을 하고 있다. 그리고 순서 있는 집단, 순서 있는 분야, 그리고 지역 분야의 이론들.
0이 아닌 어떤 두 원소라도 비교가 안 되는 대수학적 구조는 다른 원소에 대해서는 어느 것도 극소수라는 의미에서 아르키메데스라고 한다. 0이 아닌 원소 쌍을 가진 구조로, 그 중 하나는 다른 한 요소에 대해 극소수라고 하며, 비 아르키메데스라고 한다. 예를 들어, 아르키메데스인 선형 순서가 있는 그룹은 아르키메데스 그룹이다.
이것은 약간 다른 공식으로 다양한 맥락에서 정밀하게 만들어질 수 있다. 예를 들어, 순서가 정해진 분야의 맥락에서, 실수의 장은 아르키메데스지만, 실제 계수의 합리적 함수는 그렇지 않은 이 속성을 형성하는 아르키메데스의 공리를 가지고 있다.
아르키메데스 재산 이름의 역사와 유래
이 개념은 고대 그리스의 지구계와 물리학자 시라큐스의 아르키메데스의 이름을 따서 오토 스톨츠(Otto Stolz, 1880년대)가 명명했다.
아르키메데스 속성은 유클리드 원소의 5권에 정의 4로 등장한다.
크기는 서로에 대한 비율이 있다고 하며, 이 비율은 곱하면 서로 초과할 수 있다.
아르키메데스가 그것을 시니두스의 에우독수스에게 공로했기 때문에 그것은 "에우독수스의 테오렘" 또는 에우독수스의 공리라고도 알려져 있다.[3]
아르키메데스는 비록 그것이 수학적 증거가 끝났다는 것을 부인했지만, 휴리스틱스 논쟁에서 인피니티멘탈을 사용했다.
선형 순서 그룹에 대한 정의
x와 y는 선형적으로 정렬된 그룹 G의 양원소가 되도록 한다. 그 다음, 모든 자연수 n에 대해 다중 nx가 y보다 작으면, 즉 다음의 불평등이 유지되는 경우, x는 y에 대해 최소가 된다(또는 동등하게, y는 x에 대해 무한하다).
이 정의는 절대값을 취함으로써 그룹 전체로 확장될 수 있다.
그룹 G는 x가 y에 대해 최소인 쌍(x, y)이 없는 경우 Archimedeans이다.
또한 K가 단위 (1)을 가진 대수 구조(예: 링)인 경우 K에도 유사한 정의가 적용된다. x가 1에 대해 최소인 경우 x는 최소인 원소다. 마찬가지로 y가 1에 대해 무한하다면 y는 무한요소다. 대수구조 K는 무한한 원소가 없고 극소수의 원소가 없다면 아르키메데스 구조다.
순서 필드
순서가 지정된 필드에는 다음과 같은 몇 가지 추가 속성이 있다.
- 합리적인 숫자들은 모든 주문된 분야에 내재되어 있다. 즉, 모든 순서가 지정된 필드는 특성 0을 가진다.
- x가 최소인 경우 1/x는 무한이고, 그 반대의 경우도 무한하다. 따라서 필드가 아르키메데스인지 검증하기 위해서는 극소수의 요소가 없는지만 확인하거나 무한대의 요소가 없는지 확인하는 것으로 충분하다.
- x가 최소값이고 r rx는 합리적인 숫자로, 그러면 rx는 또한 극소수다. 그 결과, 일반요소 c에 주어진 세 개의 숫자 c/2, c, 2c는 모두 최소치 또는 모든 비소수치 중 하나이다.
이 설정에서 아르키메데스의 공리라고 불리는 다음 문구가 정확히 들어 있을 때 순서가 정해진 필드 K는 아르키메데스가 된다.
- "x를 K의 어떤 요소가 되게 하라. 그러면 n > x와 같은 자연수 n이 존재한다."
또는 다음과 같은 특성을 사용할 수 있다.
정규화된 필드에 대한 정의
"Archimedean"이라는 한정자는 또한 다음과 같이 하나의 가치 있는 분야와 하나의 가치 있는 분야보다 규범된 공간의 순위 이론에서 공식화된다. F는 절대값 함수가 부여된 필드로, 즉, 0이 아닌 실제 숫자 0과 필드 요소 0을 연결하고 0이 아닌 각 x with F와 의 실수 x x 을(를) 하고 x= = x 와 + 을(를)로 만족시키는 함수로 한다.+ + 그러면 0이 아닌 x ∈ F에 다음과 같은 자연수 n이 존재하면 F는 Archimedies라고 한다.
마찬가지로, n개의 항이 각각 0이 아닌 벡터 x와 동일한 경우 n개의 합이 n의 충분히 큰 n에 대해 1보다 큰 규범을 갖는 경우, 규범 공간은 아르키메데스 공간이다. 절대값 또는 표준 공간을 가진 필드는 아르키메데스 또는 초경량 삼각형 불평등이라고 불리는 더 강한 조건을 만족한다.
비 아르키메데스 표준 선형 공간의 개념은 A에 의해 도입되었다. 에프 몬나.[4]
예시 및 비예시
실수의 아르키메데스 속성
합리적인 숫자의 필드에는 사소한 x= 이(가) 0일 때, 더 일반적인 = x 2 p-adic 절대값 함수 중 하나를 할당할 수 있다. 오스트로우스키의 정리로는 합리적 숫자에 대한 모든 비교 절대값이 통상적인 절대값이나 어떤 p-adic 절대값과 동등하다. 이성적 분야는 비종교적 절대값과 관련하여 완전하지 않다; 사소한 절대값과 관련하여 이성적 분야는 별개의 위상학적 공간이므로 완전하다. 통상적인 절대값(순서로부터)에 관한 완성은 실수의 분야다. 이 공사에 의해 실제 숫자의 필드는 주문된 필드로서나 표준화된 필드로서 Archimedeans가 된다.[5] 한편, 다른 비경쟁적 절대값과 관련된 보완은 p-adic 번호의 필드를 제공하는데, 여기서 p는 p-adic 정수(아래 참조)이며, p-adic 절대값이 초계량 특성을 만족하기 때문에 p-adic 숫자 필드는 비-아카이브 필드(순서된 필드로 만들 수 없음)이다.
실수의 자명론에서 비제로 최소 실수의 비존재성은 다음과 같이 최소 상한 속성에 의해 암시된다. 모든 양의 인피니티몰로 구성된 세트를 Z로 표시한다. 이 세트는 위쪽에 1로 경계되어 있다. 이제 Z가 비어 있지 않다는 모순을 가정해보자. 그러면 최소 상한 c를 가지는데, 이것도 양성이므로 c/2 < c < 2c. c는 Z의 상한이고 2c는 c보다 절대적으로 크므로, 2c는 양의 최소값이 아니다. 즉, 1/n < 2c의 자연수 n이 있다. 반면에, c/2는 양의 최소치로서, 최소 상한의 정의에 따르면 c/2와 c 사이에 최소치 x가 있어야 하고, 1/k < c/2 ≤ x인 경우 x는 최소치가 아니어야 하기 때문이다. 그러나 1/(4n) < c/2> 따라서 c/2는 무한하지 않고, 이것은 모순이다. 이것은 결국 Z가 비어 있다는 것을 의미한다: 긍정적이고 극소수의 실수는 없다.
최소 상한 속성이 그러한 맥락에서 실패할 수 있음에도 불구하고, 실제 숫자의 아르키메데스 속성은 건설적인 분석에서도 유지된다.
비아키메데스 순번 필드
아르키메데스가 아닌 순서된 장의 예를 들면, 실제 계수를 갖는 합리적인 기능의 장을 취한다.(합리적 함수는 하나의 다항식으로 다른 다항식으로 나누어서 표현할 수 있는 함수로서, 우리는 이것이 분모의 선행 계수가 되는 방식으로 이루어진다고 가정할 것이다. 양수) 이 필드를 순서형 필드로 만들려면 추가 및 곱셈 작업과 호환되는 순서를 할당해야 한다. 이제 f > g는 f - g > 0일 경우에만, 그래서 우리는 어떤 이성적인 기능이 양성으로 간주되는지 말하기만 하면 된다. 분자의 선행계수가 양이면 양수함수를 호출한다.(이 순서가 잘 정의되어 있고 덧셈과 곱셈이 호환되는지 반드시 확인해야 한다.) 이 정의에 의해 이성함수 1/x는 양성이지만 이성함수 1보다 작다. 실제로 n이 자연수라면 n(1/x) = n/x는 양수지만 n이 아무리 크더라도 여전히 1보다 작다. 따라서 이 분야에서는 1/x가 소수점이다.
이 예는 다른 계수에 일반화된다. 실제 계수 대신 합리적으로 합리적인 함수를 취하면 계수 가능한 비 아르키메데스 순서가 있는 필드를 생성한다. 계수를 다른 변수(예: y)의 합리적인 함수로 간주하면 다른 순서 유형의 예가 생성된다.
비아키메데스 가치 필드
p-adic 메트릭과 p-adic 숫자 필드가 부여된 합리적 숫자의 필드는 절대값이 있는 필드로 아르키메데스 속성을 가지고 있지 않다. 아르키메데스의 모든 평가 필드는 일반적인 절대값의 힘을 가진 복잡한 숫자의 하위 필드와 등축적으로 이형화된다.[6]
Archimedeans 순서 필드의 등가 정의
선형적으로 정렬된 모든 필드 K에는 순서된 하위 필드, 즉 K의 승수 단위 1에 의해 생성된 하위 필드로서 이성(이형성 사본)이 포함되며, 이는 순서된 부분군으로 정수를 포함하고, 순서된 단일체로서 자연수를 포함한다. 그 후 이성들의 내재는 K에 있는 이성, 정수, 자연수에 대해 말하는 방법을 제공한다. 다음은 이러한 하부구조 측면에서 아르키메데스 영역의 동등한 특성이다.[7]
- 자연수는 K에서 일치한다. 즉, K의 모든 요소는 어떤 자연수보다 적다. (무한한 요소가 존재하는 경우는 해당되지 않는다.) 따라서 아르키메데스 들판은 자연수가 제한 없이 증가하는 들판이다.
- 0은 집합 {1/2, 1/3, 1/4, ...}의 최소값이다. (K가 양의 최소값을 포함하면 0은 최대 하한이 아닐 것이다.)
- 양과 음의 이성 사이의 K의 요소 집합은 개방적이지 않다. 그 이유는 집합이 모든 infinitesimal로 구성되기 때문인데, 이는 nonzero infinitimal이 없을 때 단지 집합 {0}에 불과하며, 그렇지 않으면 최소 또는 최대 nonzero infinitimal이 존재하지 않는다. 두 경우 모두 Infiniteimals 집합이 닫히는 것을 관찰하십시오. 후자의 경우, (i) 모든 극소수는 모든 양성적 이성보다 적으며, (ii) 가장 큰 소수도, 최소한의 양성적 이성도 없으며, (iii) 그 사이에 다른 어떤 것도 없다. 따라서 아르키메데스가 아닌 모든 순서는 불완전하고 연결이 끊긴다.
- K의 어떤 x에 대해서도 x보다 큰 정수 집합은 최소 요소를 갖는다. (x가 음의 무한 수량이라면 모든 정수는 그것보다 클 것이다.)
- K의 모든 비어 있지 않은 열린 간격에는 합리적인 것이 포함되어 있다. (x가 양의 무한대인 경우, 열린 간격(x, 2x)은 무한히 많은 무한대의 무한대(infiniteimals)를 포함하지만 단 하나의 합리성은 포함하지 않는다.)
- 이성들은 sup와 inf 둘 다에 관해서 K에 밀집되어 있다. (즉, K의 모든 요소는 어떤 이성들의 sup과 다른 이성들의 inf이다.) 그러므로 아르키메데스 장은 이성적 요소를 촘촘히 배합하는 모든 질서 있는 분야라는 의미에서 이성들의 밀도 높은 순서 확장이다.
참고 항목
- 0.999... – 숫자 1의 대체 소수점 확장
- 아르키메데스의 순서가 지정된 벡터 공간 – 벡터 공간의 이항 관계
- 실수의 구성 – 실수의 자명적 정의
메모들
- ^ https://www.math.cuhk.edu.hk/course_builder/2021/math2050c/MATH%202050C%20Lecture%204%20(Jan%2021).pdf
- ^ P의 G. 피셔(1994) 에를리히(edd.), 실수, 실수의 일반화, 연속체의 이론, 107-145, 클루워 학술
- ^ Knopp, Konrad (1951). Theory and Application of Infinite Series (English 2nd ed.). London and Glasgow: Blackie & Son, Ltd. p. 7. ISBN 0-486-66165-2.
- ^ Monna, A. F. (1943). "Over een lineaire P-adische ruimte". Nederl. Akad. Wetensch. Verslag Afd. Natuurk. (52): 74–84. MR 0015678.
- ^ 닐 코블리츠, "p-adic Numbers, p-adic Analysis and Zeta-Functions", Springer-Verlag, 1977.
- ^ 1990년 뉴욕 데커의 Shell, Niel, Topological Fields and Near Valuations, Dekker, Neigh Valuations. ISBN 0-8247-8412-X
- ^ 셰히터 1997, §10.3
참조
- Schechter, Eric (1997). Handbook of Analysis and its Foundations. Academic Press. ISBN 0-12-622760-8. Archived from the original on 2015-03-07. Retrieved 2009-01-30.
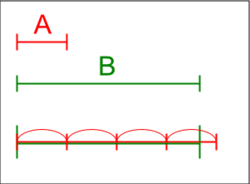







 (가)
(가)


