횡단성(수학)

수학에서 횡단성은 공간이 어떻게 교차할 수 있는지를 설명하는 개념이다; 횡단성은 접선의 "반대자"로 볼 수 있고, 일반적인 위치에서 역할을 한다. 그것은 미분 위상에서의 일반적인 교차점에 대한 생각을 공식화한다. 교차점에서 교차하는 공간의 선형화를 고려하여 정의한다.

정의

구면 가로 곡선

구체 표면의 비횡단 곡선

주어진 유한차원 매끄러운 다지관의 두 개의 서브매니폴드는 교차로마다 그 지점에서 각각의 분리된 접선 공간이 함께 그 지점에서 주변 다지관의 접선 공간을 생성한다면 횡단적으로 교차한다고 한다.^[1] 교차하지 않는 다지관은 빈 듯 횡방향이다. 다지관이 보완 치수(즉, 그 치수가 주변 공간의 치수에 더해진 경우), 조건이란 주변 다지관에 대한 접선 공간이 두 개의 작은 접선 공간의 직접적인 합임을 의미한다. 교차점이 횡단적인 경우, 교차점은 코드장이 두 다지관의 코드 합계와 동일한 하위 관리형식이 된다. 횡단성 조건이 없는 경우 교차점은 일종의 단수점을 갖는 하위 관리 대상이 되지 못할 수 있다.

특히 이는 보완적 차원의 횡단적인 서브매니폴드가 격리된 지점(즉, 0 매니폴드)에서 교차한다는 것을 의미한다. 서브매니폴드와 주변 다지관이 모두 방향인 경우, 이들의 교차점은 방향이다. 교차점이 0차원일 때 방향은 각 점의 플러스 마이너스일 뿐이다.

One notation for the transverse intersection of two submanifolds $L_{1}$ and $L_{2}$ of a given manifold $M$ is $L_{1}\pitchfork L_{2}$ . This notation can be read in two ways: either as “ $L_{1}$ 및 L ${\$ $L_{1}\cap L_{2}$ ${2$ }}: 교차 교차 $L_{2}$ " 또는 L $L_{1}$ $displaystyle L_{1}\cap L_{2$ }}: L 1 ${\$ 와 $L_{1}$ $L_{2}$ ${\$ }}의 $L_{1}\cap L_{2}$ $L_{2}$ 설정 이교차로에 대한 대체 표기법이다. 이 표기법에서 횡단성의 정의는 다음과 같다.

L_{1}\pitchfork L_{2}\iff \ forall p\in L_{1}\cap L_{2},T_{p=T_{p}L_{1}+T_{p}L_{2}.

지도 횡단성

한 쌍의 서브매니폴드 횡단성에 대한 개념은 이미지 교차점의 프리이미지를 따라 접선 공간의 푸시포워드(pushforward)가 앰브의 전체 접선 공간을 생성하는지를 질문함으로써 서브매니폴드와 주변 다지관의 지도 또는 주변 다지관의 지도 한 쌍으로 쉽게 확장된다.이엔트 ^[2]다지관 지도가 임베딩되어 있다면 이는 서브매니폴드의 전이성에 해당한다.

다양한 차원에 대한 횡단성의 의미

횡단성은 주변 공간에 따라 달라진다. 표시된 두 곡선은 평면에 포함된 것으로 간주할 때 가로로 표시되지만, 3차원 공간에서 평면에 포함된 것으로 간주할 경우에는 표시되지 않는다.

가로 지도 $f_{1}:L_{1}\to M$ $f_{1}:L_{1}\to M$ : $f_{1}:L_{1}\to M$ $f_{1}:L_{1}\to M$ → $f_{1}:L_{1}\to M$ ${\displaystyle f_{1$ }가 있다고 가정합시다 $.$ $L_{1}\to M}$ 및 $f_{1}:L_{1}\to M$ $f_{2}:L_{2}\to M$ $f_{2}:L_{2}\to M$ : $f_{2}:L_{2}\to M$ $f_{2}:L_{2}\to M$ → M ${\displaystyle f_{2}:$ $L_{1},L_{2}$ ${2}\to M}$ 여기서 $f_{2}:L_{2}\to M$ L $L_{1},L_{2}$ , $L_{1},L_{2}$ $L_{1},L_{2}$ ${\$ $L_$ ${2$ }} 및 $L_{1},L_{2}$ M $M$ 은(는) 치수 $\ell _{1},\ell _{2}$ $m$ 1, $\ell _{1},\ell _{2}$ 2 ${\$ $m$ ${\displaystytym}$ 을 $M$ (으)하는 다지이다.

횡단성의 의미는 $M,L_{1}$ , $M,L_{1}$ 1 ${\$ L $M,L_{1}$ $L_{2}$ ${\$ }}의 상대적 치수에 따라 많이 다르다 $L_{2}$ $\ell _{1}+\ell _{2}=m$ $\ell _{1}+\ell _{2}=m$ + $\ell _{1}+\ell _{2}=m$ 2 $\ell _{1}+\ell _{2}=m$ = m ${\displaystyle \ell _{1}+\ell _{2}=m$ 일 때 횡성과 접선성의 관계가 가장 명확하다.

세 가지 경우를 따로 고려해 볼 수 있다.

$\ell _{1}+\ell _{2}<m$ $\ell _{1}+\ell _{2}<m$ + $\ell _{1}+\ell _{2}<m$ $\ell _{1}+\ell _{2}<m$ < m ${\displaystyle \ell _{1}+\ell _{2}<m$ 에서 $L_{1}$ $L_{1}$ 1 ${\$ 1}과 $L_{1}$ L ${\$ 2}}의 $L_{2}$ 접선 공간 이미지가 어느 지점에서나 $M$ ${\displaystystystyle M}$ 의 $M$ 접선 공간에 걸쳐지는 불가능하다. 따라서 $f_{1}$ $f_{1}$ ${\$ }와 $f_{1}$ $f_{2}$ $f_{2}$ ${\$ }} 사이의 교차는 횡단할 수 없다 $f_{2}$ . 단, 비 교차 다지관은 그 조건을 공허하게 만족시키므로 횡방향으로 교차한다고 할 수 있다.
$\ell _{1}+\ell _{2}=m$ $\ell _{1}+\ell _{2}=m$ + $\ell _{1}+\ell _{2}=m$ $\ell _{1}+\ell _{2}=m$ = m $\ell _{1}+\ell _{2}=m$ 일 $\ell _{1}+\ell _{2}=m$ 때 $L_{2}$ $L_{1}$ $L_{1}$ ${\$ ${$ 1 $}:{1$ } $L_{2}$ L 2 ${\$ 2}}의 접선 공간은 교차로에서 $M$ ${\displaystystyle M}$ 의 $M$ 접선 공간에 직접 합해야 한다. 따라서 이들의 교차점은 고립된 부호점, 즉 0차원 다지관으로 구성된다.
$\ell _{1}+\ell _{2}>m$ $\ell _{1}+\ell _{2}>m$ + $\ell _{1}+\ell _{2}>m$ $\ell _{1}+\ell _{2}>m$ > m $\ell _{1}+\ell _{2}>m$ 이 합은 직접적일 필요가 $\ell _{1}+\ell _{2}>m$ 없다. $f_{1}$ $f_{1}$ 1 ${\$ }와 $f_{1}$ $f_{2}$ $f_{2}$ ${\$ }}이 임베디드 서브매니폴드의 경우처럼 교차로에서 임모션인 경우에는 $f_{2}$ 직접적일 수 없다. 만약 지도가 몰입형이라면, 이미지의 교차점은 치수 $\ell _{1}+\ell _{2}-m.$ 1 $\ell _{1}+\ell _{2}-m.$ + $\ell _{1}+\ell _{2}-m.$ $\ell _{1}+\ell _{2}-m.$ - $\ell _{1}+\ell _{2}-m.$ . ${\displaystyle \ell _{1}+\ell _{2}-m$ 의 다지관이 될 것이다 $.$ $}$

교차로제품

어떤 두 개의 매끄러운 서브매니폴드가 있을 경우, 결과 서브매니폴드가 고정 서브매니폴드와 교차적으로 교차하도록 임의의 소량으로 둘 중 하나를 섭동할 수 있다. 그러한 동요는 다지관 또는 그 교차점의 동질학 등급에 영향을 미치지 않는다. 예를 들어, 보완 치수의 다지관이 횡단적으로 교차하는 경우, 다지관을 다른 횡단 교차점에 동위원소화해도 교차점 수의 부호화된 합계는 변하지 않는다. (교차점은 부호를 무시하고 모듈로 2를 세어 코어저 불변제를 얻을 수 있다.) 이것은 모든 차원의 동음이의학 클래스에 있는 이선형 교차점 제품으로, 코호몰리에 관한 컵 제품에 Poincaré가 이중이다. 컵 제품과 마찬가지로 교차 제품은 등급이 정해져 있다.

횡단 교차로 예

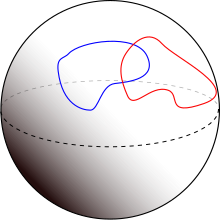
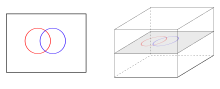
횡단성에 대한 가장 단순한 비비례는 표면의 호이다. 두 호 사이의 교차점은 접선이 아닌 경우에만 횡방향이다. 즉, 표면에 대한 접선 평면 내부의 접선 선이 구별된다.

3차원 공간에서는 가로곡선이 교차하지 않는다. 표면을 가로지르는 곡선은 점으로 교차하고, 서로 가로지르는 표면은 곡선으로 교차한다. 한 점에서 표면에 접하는 곡선(예: 표면에 놓여 있는 곡선)은 지표면을 횡단적으로 교차하지 않는다.

$여기$ 좀 더 전문화된 예가 있다: G $G$ 이 $G$ (가) 단순한 Lie 그룹이고 ${\mathfrak {g}}$ ${\$ { $g}}$ 이 ${\mathfrak {g}}$ (가) Lie 대수라고 가정하자. By the Jacobson–Morozov theorem every nilpotent element $e\in {\mathfrak {g}}$ can be included into an ${\mathfrak {sl_{2}}}$ -triple $(e,h,f)$ . The representation theory of ${\mathfrak {sl_{2}}}$ tells us that ${\mathfrak {g}}=[{\mathfrak {g}},e]\oplus {\mathfrak {g}}_{f}$ = ${\mathfrak {g}}=[{\mathfrak {g}},e]\oplus {\mathfrak {g}}_{f}$ [ g ${\mathfrak {g}}=[{\mathfrak {g}},e]\oplus {\mathfrak {g}}_{f}$ , ${\mathfrak {g}}=[{\mathfrak {g}},e]\oplus {\mathfrak {g}}_{f}$ ${\mathfrak {g}}=[{\mathfrak {g}},e]\oplus {\mathfrak {g}}_{f}$ ${\mathfrak {g}}=[{\mathfrak {g}},e]\oplus {\mathfrak {g}}_{f}$ ${\mathfrak {g}}=[{\mathfrak {g}},e]\oplus {\mathfrak {g}}_{f}$ ${\$ { $g},e]\plus {\mathfrak{g}_{f$ The space $[{\mathfrak {g}},e]$ is the tangent space at $e$ to the adjoint orbit ${\rm {{Ad}(G)e}}$ and so the affine space $e+{\mathfrak {g}}_{f}$ intersects the orbit of $e$ transversally. $e+{\mathfrak {g}}_{f}$ e $e+{\mathfrak {g}}_{f}$ + $e+{\mathfrak {g}}_{f}$ f ${\$ e $+{\mathfrak{g}_{f}}$ 는 $e+{\mathfrak {g}}_{f}$ 피터 슬로도위 다음에 나오는 "슬로도위 슬라이스"로 알려져 있다.

적용들

최적제어

변동의 미적분학 또는 관련 폰트랴긴 최대 원리를 활용하는 분야에서는 횡단성 조건이 최적화 문제에서 발견되는 해결책의 유형을 제어하는 데 자주 사용된다. 예를 들어 다음과 같은 형태의 문제에 대한 솔루션 곡선에 필요한 조건이다.

원곡선의 끝점 중 하나 또는 둘 다 고정되지 않은 경우

\int {F(x,y,y^{\prime })}dx

∫

\int {F(x,y,y^{\prime })}dx

,

\int {F(x,y,y^{\prime })}dx

, y ,

\int {F(x,y,y^{\prime })}dx

\int {F(x,y,y^{\prime })}dx

)

\int {F(x,y,y^{\prime })}dx

{\

displaystyle \int {F(x,y,y^{\prime }dx}

을(를) 최소화하십시오.

이러한 많은 문제에서, 솔루션은 솔루션 곡선이 횡단적으로 널클라인 또는 단자 조건을 설명하는 다른 곡선을 교차해야 하는 조건을 만족시킨다.

용액 공간의 부드러움

지도의 횡단성을 가설이 특수한 경우인 사르드의 정리를 이용하면 보완차원의 공간의 서브매니폴드 사이 또는 공간에 대한 서브매니폴드와 지도 사이의 횡단 교차점 자체가 매끄러운 서브매니폴드임을 알 수 있다. 예를 들어 방향 다지관의 접선 번들(즉, 벡터장)의 매끄러운 부분을 베이스에서 총 공간까지의 지도로 보고, 영점(지도 또는 서브매니폴드로 표시)을 가로로 교차하는 경우, 섹션의 0 세트(즉, 벡터장 특이점)는 부드러운 0차원 잠수함을 형성한다.기지의 형태, 즉 서명된 포인트 세트 기호는 벡터장의 지수와 일치하므로 기호의 합계(즉, 영점 세트의 기본 등급)는 다지관의 오일러 특성과 동일하다. 보다 일반적으로 방향의 매끄러운 닫힌 유한차원 다지관 위에 있는 벡터 다발의 경우, 영 단면을 가로지르는 섹션의 0 세트는 벡터 다발의 등급과 동일한 코다이멘션 베이스의 하위매니폴드가 되며, 그 호몰로지 등급은 번들의 오일러 등급에 해당하는 푸앵카레 2가 된다.

이것의 극히 특별한 경우는 다음과 같다:실제부터 실재까지의 차별화 가능한 함수가 함수의 0에서 0이 아닌 파생상품을 갖는 경우, 0은 단순하다. 즉, 그래프는 그 0에서 x축에 횡방향이다. 0의 파생상품은 곡선에 수평 접하는 것을 의미하며, 이 접선 공간과 일치한다.e x축

무한대의 예를 들어, d-bar 연산자는 리만 표면에서 거의 복합적인 다지관까지의 지도 공간 위에 있는 특정 바나흐 공간 번들의 한 부분이다. 이 조의 영점 세트는 홀로모르픽 지도로 구성된다. d-bar 연산자가 영점 섹션에 횡방향으로 표시될 수 있는 경우, 이 모듈리 공간은 부드러운 다지관이 될 것이다. 이러한 고려사항들은 사이비홀로모픽 커브 이론과 그로모프-위튼 이론에 근본적인 역할을 한다.(이 예에서는 바나흐 공간을 다루기 위해서는 횡단성의 정의를 다듬어야 한다는 점에 유의하라!)

문법

"횡단"은 명사이고, 형용사는 "횡단"이다.

J.H.C.에서 인용하다. 화이트헤드, 1959년^[3]

참고 항목

횡단성 정리

메모들

^ 기일민과 폴락 1974년 페이지 30.
^ 구이레민과 폴락 1974년 페이지 28.
^ 허쉬(1976), 페이지 66

참조

Thom, René (1954). "Quelques propriétés globales des variétés differentiables". Comm. Math. Helv. 28 (1): 17–86. doi:10.1007/BF02566923. S2CID 120243638.
Guillemin, Victor; Pollack, Alan (1974). Differential Topology. Prentice-Hall. ISBN 0-13-212605-2.
Hirsch, Morris (1976). Differential Topology. Springer-Verlag. ISBN 0-387-90148-5.

[1] 기일민과 폴락 1974년 페이지 30.

[2] 구이레민과 폴락 1974년 페이지 28.

[3] 허쉬(1976), 페이지 66

[1]

[2]

[3]

Search