곱셈표
Multiplication table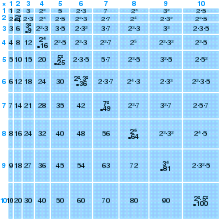
곱셈표(, )는 수학에서 대수적 체계에 대한 곱셈 연산을 정의하는 데 사용되는 수학적 표입니다.
십진법 곱셈표는 전통적으로 전 세계 초등 산수에서 필수적인 부분으로 가르쳐졌는데, 이는 10진법으로 산술 연산의 기초를 다지기 때문입니다.많은 교육자들은 표를 9×9까지 외우는 것이 필요하다고 믿고 있습니다.[1]
역사
전근대

가장 오래된 것으로 알려진 곱셈표는 약 4000년 전 바빌로니아 사람들에 의해 사용되었습니다.[2]하지만, 그들은 60의 베이스를 사용했습니다.[2]10을 밑으로 하는 가장 오래된 알려진 표는 중국 전국시대인 기원전 305년경의 죽간에 있는 중국 십진법 곱셈표입니다.[2]

곱셈표는 때때로 고대 그리스 수학자 피타고라스 (기원전 570–495)의 것으로 여겨집니다.그것은 또한 많은 언어(예를 들어 프랑스어, 이탈리아어, 러시아어)로 피타고라스의 식탁이라고도 불리며, 때로는 영어로도 사용됩니다.[4]신피타고라스주의의 추종자인 그리스-로마의 수학자 Nichomachus (60–120 AD)는 산술 입문에 곱셈표를 포함시킨 반면, 현존하는 가장 오래된 그리스 곱셈표는 서기 1세기로 거슬러 올라가는 밀랍 판 위에 있으며 현재 대영 박물관에 소장되어 있습니다.[5]
서기 493년, 아키텐의 빅토리우스는 98열의 곱셈표를 작성했는데, 이 표는 로마 숫자로 2에서 50번까지의 모든 숫자의 곱을 주고 행들은 "1,000으로 시작해서 수백에서 100으로 내려오고, 수십에서 10으로 내려가고, 그 다음에 1에서 1로 내려오고, 분수는 1/144로 내려간다"는 것이었습니다.[6]
근세
수학자 존 레슬리([7]John Leslie)는 1820년 저서 산술철학에서 숫자를 한 번에 숫자 쌍으로 곱할 수 있는 99 × 99까지의 곱셈표를 발표했습니다.Leslie는 또한 어린 학생들이 곱셈표를 50x50까지 외울 것을 권했습니다.
아래 그림은 12 × 12까지의 표를 보여주는데, 이것은 요즘 영어 세계 학교에서 흔히 사용되는 크기입니다.
| × | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 2 | 0 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 |
| 3 | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | 33 | 36 |
| 4 | 0 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | 44 | 48 |
| 5 | 0 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 |
| 6 | 0 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | 66 | 72 |
| 7 | 0 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 | 77 | 84 |
| 8 | 0 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 | 88 | 96 |
| 9 | 0 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 | 99 | 108 |
| 10 | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 110 | 120 |
| 11 | 0 | 11 | 22 | 33 | 44 | 55 | 66 | 77 | 88 | 99 | 110 | 121 | 132 |
| 12 | 0 | 12 | 24 | 36 | 48 | 60 | 72 | 84 | 96 | 108 | 120 | 132 | 144 |
그러나 중국에서는 정수의 곱셈이 교환적이기 때문에 많은 학교에서 아래와 같이 작은 표를 사용합니다.일부 학교에서는 1이 곱셈 동일성이기 때문에 첫 번째 열을 제거하기도 합니다.
| 1 | 1 | ||||||||
| 2 | 2 | 4 | |||||||
| 3 | 3 | 6 | 9 | ||||||
| 4 | 4 | 8 | 12 | 16 | |||||
| 5 | 5 | 10 | 15 | 20 | 25 | ||||
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | |||
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | ||
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 |
| × | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
곱셈의 전통적인 암기 학습은 다음과 같은 형태로, 표의 열을 암기하는 것에 기초했습니다.
1 × 10 = 10
2 × 10 = 20
3 × 10 = 30
4 × 10 = 40
5 × 10 = 50
6 × 10 = 60
7 × 10 = 70
8 × 10 = 80
9 × 10 = 90
완전한 숫자 문장으로 된 열에 곱셈표를 쓰는 이 형식은 보스니아 헤르체고비나와 같은 일부 국가에서는 [citation needed]위의 현대적인 그리드 대신 여전히 사용됩니다.
표의 패턴
곱셈표에는 표를 더 쉽게 외울 수 있도록 도와주는 패턴이 있습니다.아래의 수치를 사용합니다.
| → | → | |||||||||
| ↑ | 1 | 2 | 3 | ↓ | ↑ | 2 | 4 | ↓ | ||
|---|---|---|---|---|---|---|---|---|---|---|
| 4 | 5 | 6 | ||||||||
| 7 | 8 | 9 | 6 | 8 | ||||||
| ← | ← | |||||||||
| 0 | 5 | 0 | ||||||||
| 그림 1: 홀수 | 그림 2: 짝수 | |||||||||

그림 1은 1, 3, 7, 9의 배수에 사용됩니다.그림 2는 2, 4, 6, 8의 배수에 사용됩니다.이 패턴은 5를 제외하고 0부터 10까지의 숫자의 배수를 기억하는 데 사용될 수 있습니다.곱하고 있는 숫자에서 시작하는 것처럼, 0을 곱하면 0에 머무르게 됩니다(0은 외부이므로 화살표가 0에 영향을 미치지 않으며, 그렇지 않으면 0은 영구 사이클을 생성하기 위한 링크로 사용됩니다).패턴은 또한 10의 배수와 함께 작동합니다. 1에서 시작하여 단순히 0을 더하여 10을 제공한 다음 패턴의 모든 숫자를 "1" 단위에 평소처럼 적용합니다.
예를 들어, 7의 모든 배수를 호출하는 경우:
- 첫 번째 사진의 7을 보고 화살표를 따라 가세요.
- 화살표 방향의 다음 숫자는 4입니다.따라서 7 다음 숫자는 4로 끝나는 14입니다.
- 화살표 방향의 다음 숫자는 1입니다.그러니까 14 뒤에 1로 끝나는 다음 숫자, 즉 21을 생각해 보세요.
- 이 열의 맨 위로 올라온 후 다음 열의 맨 아래부터 시작하여 같은 방향으로 이동합니다.숫자는 8입니다.그러니까 21 이후의 숫자는 8, 즉 28로 끝나는 숫자를 생각해 보세요.
- 63번에 해당하는 마지막 숫자인 3번까지 동일하게 진행합니다.
- 그다음에 밑에 있는 0을 사용합니다.70에 해당합니다.
- 그럼 7번부터 다시 시작합니다.이번에는 77에 해당될 것입니다.
- 계속 이렇게.
추상대수학에서
표는 또한 그룹, 필드, 링 및 기타 대수 시스템에 대한 이진 연산을 정의할 수 있습니다.그러한 맥락에서 그것들은 케일리 테이블이라고 불립니다.유한장 Z에5 대한 덧셈 및 곱셈 표는 다음과 같습니다.
- 모든 자연수 n에 대하여, 고리 Z에n 대한 덧셈과 곱셈표도 있습니다.
|
|
다른 예는 group 및 octonion을 참조하십시오.
중국어와 일본어 곱셈표
헤이조궁에서 발견된 목간은 10개 미만의 곱에서 如 문자를 공유하기 때문에 순자수안징과 같은 중국의 수학 논문을 통해 일본에 곱셈표가 전해졌을 가능성을 시사합니다.중국어와 일본어는 곱셈표를 9×9까지 학습할 수 있도록 학생들에게 가르쳐주는 81개의 짧고 쉽게 기억할 수 있는 문장으로 이루어진 비슷한 체계를 공유합니다.현재의 사용법에서, 10개 미만의 제품을 표현하는 문장은 두 언어 모두에서 하나의 추가적인 입자를 포함합니다.현대 중국어의 경우 이것은 得(dé)이고, 일본어의 경우 이것은 が(ga)입니다.수안판이나 소로반으로 계산을 연습하는 사람들에게 유용한데, 십자릿수로 시작하지 않는 제품을 입력할 때 문장을 보면 한 열을 오른쪽으로 이동해야 하기 때문입니다.특히 일본어 곱셈표는 일부 특정 인스턴스(예: 산로쿠를 사부로쿠로 대체)에서 숫자에 대해 비표준 발음을 사용합니다.
| × | 1이치 | 2니 | 3산 | 4shi | 5고 | 6 로쿠 | 7시치 | 8하 | 9쿠 |
|---|---|---|---|---|---|---|---|---|---|
| 1 in | 이치 가이치 | 이니니니 | 산에서 | 시가시에 | 고고고 | 로쿠가 로쿠에서 | 인시치가시치 | 하치하치하치하치하치하치하치하치하치하. | 인쿠가쿠 |
| 2니 | 니이치 가니 | 구니시 | 니상가로쿠 | 니시가하치 | 니고쥬 | 니로쿠쥬니 | 니시치 쥬시 | 니하치 주로쿠 | 니쿠주하치 |
| 3산 | 산이치가산 | 산니가 로쿠 | 사잔가쿠 | 산시쥬니 | 산고주고 | 사부로쿠 주하치 | 산시치 니주이치 | 산파니쥬시 | 산쿠니쥬시치 |
| 4shi | 시이치가시 | 샤이가하치 | 시산쥬니 | 시즈쥬로쿠 | 시고니쥬 | 시로쿠니쥬시 | 니주하치 시이치 | 시하산쥬니 | 시쿠 산쥬로쿠 |
| 5고 | 이치가고 | 고니쥬 | 주고에 가다 | 신쥬에 가다 | 고니쥬고 | 로쿠산쥬에 가다 | 고시치 산쥬고 | 하시쥬에 가다 | 고쿠시쥬고 |
| 6 로쿠 | 로쿠이치가 로쿠 | 로쿠니쥬 | 로쿠산주하치 | 로쿠시니쥬시 | 로쿠고산쥬 | 로쿠로쿠 산쥬로쿠 | 로쿠시치시쥬니 | 로쿠하시즈하치 | 롯쿠 고쥬시 |
| 7시치 | 시치이치가시치 | 시치니쥬시 | 시치 산니주이치 | 시치신니주하치 | 시치고 산쥬고 | 시치로쿠시즈니 | 시치시즈쿠 | 시치하고쥬로쿠 | 시치쿠로쿠쥬산 |
| 8하치 | 하치이치가하치 | 하치니쥬로쿠 | 하치산니쥬시 | 하치시 산쥬니 | 하치고시쥬 | 하치로쿠시즈하치 | 하치시치 고쥬로쿠 | 하파 로쿠쥬시 | 하쿠시치쥬니 |
| 9쿠 | 쿠이치가쿠 | 쿠니주하치 | 쿠사니주시치 | 쿠시산쥬로쿠 | 고고시쥬고 | 쿠로쿠 고쥬시 | 구시치 로쿠쥬산 | 쿠하시치쥬니 | 쿠쿠하치주이치 |
전국 10진법 곱셈 대나무 전표
청화 대나무 전표(清華簡) 모음집에 있는 기원전 305년 전국시대의 대나무 전표 21개 묶음은 십진법 곱셈표의 세계 최초 사례로 알려져 있습니다.
미국의 표준 기반 수학 개혁
1989년에, 전국 수학 교사 협의회 (NCTM)는 모든 학생들이 고차원적인 사고 기술을 배워야 한다는 믿음에 기초한 새로운 표준을 개발했습니다. 이것은 곱셈표와 같은 암기에 의존했던 전통적인 방법의 교육에 대한 강조를 줄일 것을 권고했습니다.숫자, 데이터 및 공간에서의 조사(생산자의 이름을 따서 TERC로 널리 알려짐)와 같은 널리 채택된 텍스트는 초기 판에서 곱셈표와 같은 보조 도구를 생략했습니다.NCTM은 2006년 Focial Points에서, 비록 암기가 최선의 방법인지에 대한 합의는 없지만, 기본적인 수학적 사실을 배워야 한다는 것을 분명히 했습니다.최근 몇 년 동안, 아이들이 곱셈 사실을 배울 수 있도록 도와주는 비전통적인 방법들이 많이 고안되었는데, 비디오 게임 스타일의 앱과 캐릭터 기반의 이야기를 통해 시간표를 가르치는 것을 목표로 하는 책들이 포함되어 있습니다.
참고 항목
참고문헌
- ^ Trivett, John (1980), "The Multiplication Table: To Be Memorized or Mastered!", For the Learning of Mathematics, 1 (1): 21–25, JSTOR 40247697.
- ^ a b c Qiu, Jane (January 7, 2014). "Ancient times table hidden in Chinese bamboo strips". Nature News. doi:10.1038/nature.2014.14482. S2CID 130132289.
- ^ 위키 소스:페이지 : 인기과학 월간지 26.djvu/467권
- ^ 예를 들어 존 패러의 산술 기초 논문에서
- ^ 데이비드 E.스미스(Smith, 1958), 수학의 역사, 제1권: 초등수학의 역사 총조사뉴욕: 도버 출판사(1951년 출판물의 재인쇄), ISBN 0-486-20429-4, 페이지 58, 129
- ^ 데이비드 W. 마허와 존 F.마코프스키."분수가 있는 로마 산술에 대한 문헌적 증거"고전 문헌학, 96/4 (2001년 10월), 페이지 383.
- ^ Leslie, John (1820). The Philosophy of Arithmetic; Exhibiting a Progressive View of the Theory and Practice of Calculation, with Tables for the Multiplication of Numbers as Far as One Thousand. Edinburgh: Abernethy & Walker.
- ^ "「九九」は中国伝来…平城宮跡から木簡出土". Yomiuri Shimbun. December 4, 2010. Archived from the original on December 7, 2010.
- ^ 자연 기사 2,300년 된 행렬은 세계에서 가장 오래된 십진 곱셈표입니다.
1 x 1 ~ 23 x 23