현대 삼각형 기하학

Modern triangle geometry
에밀 르모인(1840년-1912년

수학에서, 현대 삼각형 기하학 또는 새로운 삼각형 기하학은 19세기 마지막 4분의 1초 이후 대략적으로 발견되고 개발된 삼각형의 특성과 관련된 지식의 집합체이다.삼각형과 그 특성은 적어도 유클리드의 시대부터 조사 대상이었다.사실, 유클리드의 요소에는 삼각형과 관련된 네 가지 특별한 점, 즉 중심, 인센티브, 원심 및 직교점에 대한 설명이 포함되어 있습니다.비록 17세기의 파스칼과 체바, 18세기의 오일러와 19세기의 포이어바흐 그리고 많은 다른 수학자들이 삼각형의 특성에 대해 중요한 발견을 했지만, 그것은 1873년 에밀 르모인 (1840년-1912년)의 논문의 제목으로 출판되었다.Nathan Altschiller-Court에 따르면,[1][2] "삼각형의 현대 기하학의 기초를 다졌다"고 한다.르모인의 연구의 많은 부분이 출판된 미국 수학 월간지는 "이들 중 누구에게도 에밀 미셸 히아신테 르모인은 현대 삼각 [3]기하학의 운동을 시작하는 영광을 누리게 될 것입니다."라고 선언했습니다.이 논문의 출판은 19세기 마지막 4분의 1과 20세기 초에 삼각형의 성질을 조사하는데 있어 주목할 만한 관심을 불러일으켰다.1914년에[4] 출판된 클라인의 수리과학 백과사전에 실린 삼각기하학에 관한 100페이지 분량의 기사는 삼각기하학에 [5]대한 이러한 관심의 급증을 증명한다.

초기 "새로운 삼각형 기하학"이라는 표현은 르모인 점, 르모인 원, 브로카드 원, 르모인 선과 같은 삼각형과 관련된 흥미로운 물체 집합만을 가리켰다.나중에 기하학적 변환 이론의 분파였던 대응 이론은 다양한 고립된 결과에 일관성을 주기 위해 개발되었다.그것의 발전과 함께, "새로운 삼각형 기하학"이라는 표현은 삼각형과 관련된 많은 주목할 만한 물체들뿐만 아니라, 이러한 물체들을 연구하고 분류하는 데 사용되는 방법들을 나타내었다.1887년부터의 삼각형 기하학의 정의: "삼각형의 평면에서 점 M이 주어지면, 우리는 상상된 기하학적 법칙에 따라 첫 번째 점 M'에 대응하는 두 번째 점 M'을 항상 찾을 수 있다; 이 두 점 사이에 단순성이 더 많거나 덜한 기하학적 관계가 있다.그것들을 통합하는 법칙의 행운의 선택과 각각의 기하학적 법칙은 그것이 연구할 수 있는 활용 방식을 만들어낸다.(19세기와 20세기의 고대 인물과 새로운 기하학적 방법을 가르친다: 유럽과 미국의 교과서에서 새로운 삼각형 기하학이라는 제목의 회의 논문을 참조한다.2009년에 발표된 Pauline Romera-Lebret의 A(1888-1952)입니다.[6][7]

하지만, 이러한 관심의 증가는 곧 무너졌고 삼각형 기하학은 20세기 말까지 완전히 무시되었다.그의"수학의 개발"에서, 에릭 템플 벨 1940년의 방향:"20세기의 geometers 오래 전에 경건하게 기하학의 역사의 먼지 빠르게 그들의 광택이 어두워지면서 박물관 위해 이 모든 보물들을 떼어 내다."(개발 수학의 페이지의 주 323)[5]필립 현대적인 삼각형 기하학의 지위에 그의 판단을 제공한다.davis는 삼각형 [5]기하학에 대한 관심의 감소에 대한 몇 가지 이유를 제시했다.여기에는 다음이 포함됩니다.

  • 과목이 초급이고 직업적 지위가 낮다는 느낌.
  • 그것의 방법론적 가능성들의 고갈.
  • 피험자의 더 깊은 결과의 시각적 복잡성.
  • 대수학 쪽으로 시각의 하향 조정.
  • 다른 분야와의 연결 부족
  • 테셀레이션, 프랙탈, 그래프 이론 등 시각적인 내용이 강한 다른 주제와의 경쟁

현대 전자 컴퓨터의 등장으로 관심이 더욱 되살아났다.삼각기하학이 다시 전용기하학 그룹에 의해 추구되는 활발한 연구 영역이 되었다.이 부활의 전형으로서, 사람들은 "삼각형 중심"의 개념의 공식화 및 클라크 킴벌링에 의한 거의 50,000개의 삼각형 중심과 그 특성들의 목록을 포함하는 삼각 중심 백과 사전의 편찬과 또한 삼각 정육면체의 상세한 설명과 함께 삼각 정육면체 카탈로그의 편찬을 지적할 수 있다.1200개 이상의 삼각 입방체 [8][9]랄.2001년 플로리다 애틀랜틱 대학의 Paul Yiu가 설립한 오픈 액세스 저널 Forum Geometricorum도 삼각형 기하학에 대한 새로운 열정을 더욱 심화시키는 데 엄청난 자극을 주었다.안타깝게도, 2019년부터 저널은 온라인상에서 백 호를 볼 수 있지만 투고를 받지 않고 있습니다.

르모인 기하학

레모인 점

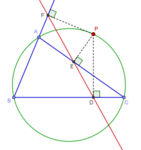
중심 G를 갖는 주어진 삼각형 ABC에서 정점을 통과하는 심미디언은 각도 A의 이등분선에서 선 AG의 반사이다.각 정점을 통과하는 삼각형에는 세 개의 심미디언이 있습니다.세 개의 심메디언이 동시에 존재하며, 일반적으로 K로 나타나는 동시성 점을 삼각 ABC의 심메디언 점 또는 그레베 점이라고 합니다.삼각형 ABC의 옆면 길이가 a, b, c이면 르모인 점의 중심 좌표는 a : b2 : c이다22.그것은 "현대 [10]기하학의 왕관 보석 중 하나"로 묘사되어 왔다.존 맥케이의 심메디아 [11]점의 역사에서 이용 가능한 수학 문헌의 세부 사항에는 이 점에 대한 몇 가지 초기 언급이 있다.

사실, symmedians의 동시성은 보다 일반적인 결과의 특별한 경우입니다.삼각형 ABC 평면상의 임의의 점 P에 대해 선 AP, BP, CP의 등각도는 동시에 각도 A(각 B, C)의 이등분선 AP의 반사인 AP(각 BP, CP)의 등각이다.동시성의 점을 P의 등교 켤레라고 한다.이 용어에서 르모인 점은 중심부의 등교 켤레이다.

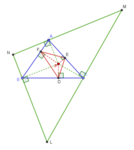
레모인 서클

삼각형의 변에 평행한 삼각형 ABC의 레모인 점을 통과하는 선의 교차점은 삼각형 ABC의 첫 번째 레모인 원이라고 불리는 원 위에 있다.첫 번째 레모인 원의 중심은 삼각형의 원주 중심과 레모인 점 사이의 중간에 위치한다.

삼각형 ABC의 레모인 점을 통해 삼각형 ABC의 변에 대한 역평행의 교차점은 두 번째 레모인 원 또는 삼각형 ABC의 코사인 원이라고 불리는 원 위에 있습니다."코사인 원"이라는 이름은 삼각형 변의 원에 의해 가로채진 세그먼트의 길이가 변의 반대 각도의 코사인에 비례하는 두 번째 르모인 원의 특성 때문이다.두 번째 레모인 원의 중심은 레모인 점입니다.

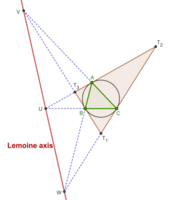
레모인 축

모든 삼각형 ABC와 그 접선 삼각형은 원근법에 있으며 원근법의 축은 삼각형 ABC의 르모인 축이라고 불립니다.그것은 삼각형 ABC의 심메디언 점의 삼선 극이며 삼각형 ABC의 [12][13]원주 원점에 대한 K의 극이기도 하다.

  • A triangle with medians (black), angle bisectors (dotted) and symmedians (red). The symmedians intersect in the symmedian point (denoted by L in the figure), the angle bisectors in the incenter I and the medians in the centroid G.

    중위수(검은색), 각도 이등분선(점) 및 심미디언(빨간색)이 있는 삼각형입니다.심메디언은 심메디언 점(그림에서 L로 표시), 인센티브 I의 각도 이등분선 및 중심 G의 중위수와 교차한다.

  • First Lemoine circle of triangle ABC. The Lemoine point K, the incenter I, the centroid G and the lines through K parallel to the sides are also shown.

    삼각형 ABC의 첫 번째 르모인 원.Lemoine 점 K, 유인제 I, 중심 G 및 변에 평행한 K를 통과하는 선도 표시됩니다.

  • Second Lemoine Circle of triangle ABC. The Lemoine point K, the incenter I, the centroid G and the lines through K antiparrallel to the sides are also shown.

    삼각형 ABC의 두 번째 레모인 원.Lemoine 점 K, 유인제 I, 중심 G 및 K 반팔라렐을 통해 변으로 가는 선도 표시된다.

  • Lemoine axis of triangle ABC. The tangential triangle is also shown.

    삼각형 ABC의 레모인 축.접선 삼각형도 표시됩니다.

초기 현대 삼각형 기하학

르모인의 논문 발표 후 삼각기하학에 대한 관심이 최고조에 달했을 때 존재했던 현대 삼각기하학의 세계를 간략히 살펴본다.이 발표는 1910년에 출판된 윌리엄 갤러틀리의 책과[14] 1929년에 처음 출판된 로저 A 존슨의 책에서[15] 논의된 주제들에 주로 기초하고 있다.

기압 삼각형

두 개의 삼각형이 같은 절추와 원주를 가지고 있으면 다공성 삼각형이라고 합니다.중심 O와 반지름이 R인 원과 중심 I와 반지름이 r인 다른 원이 주어진다면, 원 O(R)를 원으로 하고 원 I(r)를 {{1}}이면 원 안에 있는 삼각형 ABC가 무한히 존재합니다.이 삼각형들은 삼각형의 다공체계를 형성한다.참조 삼각형의 중심과 같은 특정 특수 점의 위치는 여러 삼각형을 추적하여 원과 [16]점으로 나타납니다.

심슨 선

삼각형 ABC의 원주상의 점 P에 대하여, P에서 삼각형 ABC의 변에 이르는 수직의 발은 공선이며, 공선성의 선은 [17]P의 잘 알려진 심슨 선이다.

페달 및 대향 삼각형

점 P가 주어졌을 때, P에서 삼각형 ABC의 변에 이르는 수직의 발은 D, E, F가 될 것이다.삼각형 DEF를 [18]P의 페달 삼각형이라고 합니다.P의 대향삼각형은 각각 PA, PB, PC에 수직인 A, B, C를 통과하는 선에 의해 형성된 삼각형이다.P의 페달 삼각형이 Q의 역삼각형과 동일하고, Q의 페달 삼각형이 [19][20]P의 역삼각형과 동일하다면 두 점 P와 Q를 대향점이라고 한다.

오르토폴

선 l이 주어졌을 때, P, Q, R은 삼각형 ABC에서 l까지의 정점 A, B, C에서 수직의 발이라고 하자.각각 변 BC, CA, AB에 수직인 P. Q, R을 통과하는 선은 동시에 존재하며, 일치점은 삼각형 ABC에 대한 선 l의 직교극이다.현대 삼각형 기하학에서, [21][22]직각 기둥의 특성을 다루는 많은 문헌들이 있다.

Brocard 포인트

외부 세그먼트가 각도 C, A, B 및 B, C, A의 두 개의 삼각형을 각각 포함하는 삼각형 ABC의 변 BC, CA, AB에 원을 기술하자.각도의 삼합에 의해 결정되는 원의 각 삼합은 공통점에서 교차하여 두 개의 그러한 점을 산출한다.이러한 포인트는 삼각형 ABC의 Brocard 포인트라고 불리며 보통 , 、 、 \ displaystyle \ 、 \ ^ { \ }로 표시됩니다.P가 첫 번째 Brocard 포인트(이것은 원의 첫 번째 트라이어드에 의해 결정되는 Brocard 포인트)인 경우 각도 PBC, PCA 및 PA 및 PA와 PA 및 PA는 서로 동일합니다.d 삼각형 ABC의 각도로 으로 §{\ Brocard 각도는 다음과 같습니다.

Brocard 포인트와 Brocard 각도는 몇 가지 흥미로운 [23]특성을 가지고 있습니다.[24]

일부 이미지

  • Two poristic triangles ABC and A'B'C' with respect to circles I(r) and O(R)

    원 I(r)와 O(R)에 대한 두 개의 기압 삼각형 ABC와 A'B'C'

  • Simson line of P

    P의 심슨선

  • Pedal triangle (DEF) and antipedal triangle (LMN) of P

    P의 페달 삼각형(DEF) 및 역삼각형(LMN)

  • Orthopole of line l

    직선 L의 직교극

  • First Brocard point of triangle ABC

    삼각형 ABC의 첫 번째 브로카드 점

현대 삼각형 기하학

삼각형의 중심

20세기 말기에 삼각형 기하학에 대한 관심이 되살아나는 동안 나타난 가장 중요한 아이디어 중 하나는 삼각형 중심에 대한 개념이다.1994년 클라크 킴벌링에 의해 도입된 이 개념은 [25]삼각형과 관련된 매우 많은 특별하고 주목할 만한 점들을 하나의 개념으로 통합했다.이 아이디어가 도입된 이후, 삼각형과 관련된 결과에 대한 논의는 결과가 삼각형 중심과 어떻게 연결되는지에 대한 논의 없이 거의 이루어지지 않았다.

삼각형의 중심 정의

3개의 실변수 a, b, c의 실변수 f는 다음 속성을 가질 수 있다.

  • 균질성: f(ta, tb, tc) = tn f(a, b, c)는 일부 상수 n과 모든 t > 0에 대하여.
  • 두 번째 및 세 번째 변수의 쌍대칭성: f(a, b, c) = f(a, c, b)

0이 아닌 f가 두 특성을 모두 갖는 경우 삼각형 중심 함수라고 합니다.f가 삼각형 중심 함수이고 a, b, c가 기준 삼각형의 측면 길이일 경우, 삼선형 좌표가 f(a, b, c, a) : f(b, c, a) : f(c, a, b)인 점을 삼각형 중심이라고 한다.

Clark Kimberling은 삼각형 센터 요약에 전념하는 웹사이트를 운영하고 있다.Triangle Centers 백과사전이라는 이름의 웹사이트는 거의 50,000개의 Triangle Centers에 대한 정의와 설명을 가지고 있다.

중앙선

현대 삼각형 기하학의 또 다른 통일된 개념은 중심선의 개념이다.이 개념은 삼각형과 관련된 몇 개의 특수 직선을 통합합니다.중심선의 개념은 삼각형 중심선의 개념과도 관련이 있습니다.

중앙선의 정의

ABC를 평면 삼각형으로 하고 (x : y : z )를 삼각 ABC 평면 내의 임의의 점의 삼선형 좌표라고 하자.

삼각형 ABC 평면의 직선으로, 삼선형 좌표의 방정식은 다음과 같은 형태를 가진다.

f ( a , b , c )x + g ( a , b , c )y + h ( a , b , c )z = 0

여기서 삼선형 좌표 (f ( a, b, c ) : g ( a, b, c ) : h ( a, b, c )는 삼각형 ABC [26][27]평면의 중심선이다.

중심선의 기하학적 구조

Construction of central lines.svg

X가 삼각형 ABC의 임의의 삼각형 중심이라고 하자.

  • AX, BX, C의 각도의 내부 이등분선에 각각 선 AX, BX, C를 그린다.
  • 반사선은 동시이며 동시점은 X의 등교 켤레 Y이다.
  • 세비안 AY, BY, CY가 각각 A', B', C'에서 삼각형 ABC의 반대쪽을 만나게 하자.삼각형 A'B'C'는 Y의 세비아 삼각형이다.
  • 삼각형 ABC와 세비아 삼각형 A'B'C'는 원근법에 있으며 DEF를 두 삼각형의 원근법에 대한 축으로 한다.선 DEF는 점 Y의 삼선형 극성이다.DEF 선은 삼각형 중심 X와 연관된 중심선입니다.

삼각 원뿔

삼각형 원뿔은 기준 삼각형의 평면에 있는 원뿔이며 어떤 식으로든 그것과 연관되어 있습니다.예를 들어, 기준 삼각형의 원주 및 절추부는 삼각 원뿔입니다.다른 예로는 정점을 통과하고 기준 삼각형의 중심에 그 중심이 있는 타원인 스타이너 타원, 정점을 통과하는 원뿔인 키퍼트 쌍곡선, 기준 삼각형의 중심과 직교 중심, 그리고 두 측면에서 접하는 포물선인 아르츠 포물선이 있다.f 삼각형의 꼭지점에 있는 기준 삼각형.최근에 연구된 삼각형 원뿔에는 호프스타터 타원형과 yff 원뿔형이 있다.그러나 문헌에 삼각뿔의 용어에 대한 공식적인 정의는 없다. 즉, 삼각뿔을 삼각뿔이라고 부르기 위해 원뿔이 기준 삼각형과 가져야 하는 관계는 정확하게 공식화되지 않았다.울프램매스월드는 트라이앵글 원뿔이라는 이름의 페이지를 만들어 삼각 [28]원뿔에 대한 정의를 제공하지 않고 42개 항목(모두 원뿔은 아니다)의 목록을 제공한다.

삼각 입방체

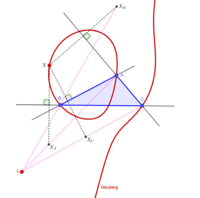
삼각형의 연구에서 입방곡선은 자연스럽게 발생한다.예를 들어 삼각형 ABC의 측방 P의 반사가 Pa, Pb, P일c 때 선 APa, BPbc, CP가 동시에 존재하는 기준 삼각형 ABC의 평면 내 점 P의 궤적은 입방곡선 Neuberg 입방체이다.이것은 버나드 길버트의 삼각입방체 카탈로그에 등재된 첫 번째 입방체이다.이 카탈로그에는 곡선의 중심 방정식, 곡선의 삼각형 중심, 곡선의 궤적 특성 및 곡선의 문헌 참조와 같은 각 곡선에 대한 정보가 포함된 1200개 이상의 삼각 입방체 목록이 있습니다.

  • Neuberg cubic (K001)

    Neuberg 큐빅 (K001)

  • McCay cubic with its three concurring asymptotes (K003)

    세 개의 동시 점근선이 있는 McCay 입방체(K003)

  • Tucker cubic (K011)

    터커 큐빅(K011)

삼각기하학 컴퓨터

컴퓨터의 진입은 20세기 말에서 20세기 초 사이에 목격된 삼각 기하학에 대한 관심의 발전 과정에 결정적인 영향을 미쳤다.컴퓨터가 이 과정에 영향을 준 방법 중 일부는 필립 [5]데이비스에 의해 설명되었습니다.컴퓨터는 삼각형 [29]기하학에서 새로운 결과를 생성하는 데 사용되어 왔습니다.2015년에 발행된 조사 기사는 컴퓨터 프로그램 "Dircoverer"[30]에 의해 발견된 중요한 새로운 결과 중 일부를 설명한다.다음 정리 샘플은 Discoverer에 의해 발견된 새로운 결과의 맛을 보여줍니다.

  • 정리 6.1 P와 Q는 삼각형 ABC의 옆선에 놓여 있지 않은 점이라고 하자.만약 P와 Q가 ABC에 대해 등교 켤레라면, 그들의 보수의 Ceva 곱은 키퍼트 쌍곡선에 놓여있다.
  • 정리 9.1일치의 Yff 중심은 인센티브의 페달 삼각형에 대한 절추부와 원주부의 내부 유사 중심이다.
  • 레스터 원은 원주 중심, 9점 중심 및 외부 및 내부 페르마 점을 통과하는 원입니다.일반화 레스터원은 적어도 4개의 삼각형 중심을 통과하는 원이다.발견자는 몇몇 일반화된 레스터 서클을 발견했다.

Sava Grozdev, Hiroshi Okumura, Deko Dekov는 컴퓨터로 발견된 유클리드 [31]기하학 백과사전을 전문으로 하는 웹 포털을 운영하고 있습니다.

레퍼런스

  1. ^ Emile Lemoine (1873). "Sur quelques propriétés d'un point remarquable du triangle". Nouvelles Annales de Mathématiques: 364–366.
  2. ^ Nathan Altschiller-Court. College Geometry. New York: Dover Publications. p. 304.
  3. ^ Smith, David Eugene (1896). "Biography of Émile-Michel-Hyacinthe Lemoine". American Mathematical Monthly. 3 (2): 29–33. doi:10.2307/2968278. JSTOR 2968278.
  4. ^ G. Berkhan; W.Fr. Meyer (1914). "10. Neuere Dreiecksgeometrie". In W.Fr. Meyer; H. Mohrmann (eds.). Geometrie. Encyklopädie der mathematischen Wissenschaften mit Einschluß ihrer Anwendungen. Vol. 3.1.2. Leipzig: B.G. Teubner. pp. 1177–1276.
  5. ^ a b c d Philip J. Davis (1995). "The Rise, Fall, and Possible Transfiguration of Triangle Geometry: A Mini-history". The American Mathematical Monthly. 102 (3): 204–214. doi:10.1080/00029890.1995.11990561.
  6. ^ Pauline Romera-Lebret. "Teaching new geometrical methods with an ancient figure in the nineteenth and twentieth centuries: the new triangle geometry in textbooks in Europe and USA (1888–1952)" (PDF). Retrieved 5 January 2022. {{cite journal}}:Cite 저널 요구 사항 journal=(도움말)
  7. ^ Bjarnadottir, K., Furinghetti, F., and Schubring, G. (editors) (2009). "Dig where you stand" – Proceedings of the Conference on "Ongoing Research in the History of Mathematics Education". University of Iceland. pp. 167–180. ISBN 978-9979-793-99-1. {{cite book}}: last1=범용명(도움말)이 있습니다.CS1 유지: 여러 이름: 작성자 목록(링크)
  8. ^ Clark Kimberling. "Encyclopedia of Triangle Centers". Clark Kimberling. Retrieved 3 January 2022.
  9. ^ Bernard Gilbert. "Catalogue of Triangle Cubics". Catalogue of Triangle Cubics. Bernard Gilbert. Retrieved 3 January 2022.
  10. ^ 를 클릭합니다Honsberger, Ross (1995), "Chapter 7: The Symmedian Point", Episodes in Nineteenth and Twentieth Century Euclidean Geometry, Washington, D.C.: Mathematical Association of America.
  11. ^ John Mackay (1892). "Early History of the Symmedian Point" (PDF). Proceedings of the Edinburgh Math. Soc. Xi: 92. Retrieved 7 January 2022.
  12. ^ Gallatly, W (1913). The Modern Geometry of the Triangle (2 ed.). London: Hodgson. p. 92.
  13. ^ Johnson, R. A. (1929). Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. Boston, MA: Houghton Mifflin. p. 294.
  14. ^ William Gallatly (1910). The Modern Geometry of the Triangle. London: Francis Hodgson. Retrieved 4 January 2022.
  15. ^ Roger A Johnson (31 August 2007). Advanced Euclidean Geometry. Dover Publications Inc. ISBN 978-0486462370.
  16. ^ William Gallatly (1910). The Modern Geometry of the Triangle. London: Francis Hodgson. Retrieved 4 January 2022. (제3장)
  17. ^ William Gallatly (1910). The Modern Geometry of the Triangle. London: Francis Hodgson. Retrieved 4 January 2022. (제4장)
  18. ^ Weisstein, Eric W. "Pedal Triangle". MathWorld--A Wolfram Web Resource. MathWorld. Retrieved 11 January 2022.
  19. ^ Weisstein, Eric W. "Antipedal Triangle". MathWorld--A Wolfram Web Resource. MathWorld. Retrieved 11 January 2022.
  20. ^ William Gallatly (1910). The Modern Geometry of the Triangle. London: Francis Hodgson. Retrieved 4 January 2022. (V-VII 장)
  21. ^ "직교공의 투영 이론", Mary Cordia Karl 수녀, The American Mathemical Monthly, 제39권, 제6호 (6월-)1932년 7월), 페이지 327~338 발행: Mathemical Association of America Stable URL: https://www.jstor.org/stable/2300757
  22. ^ Goormaghtigh, R. (1 December 1946). "1936. The orthopole". The Mathematical Gazette. 30 (292): 293. doi:10.2307/3610737. JSTOR 3610737 – via Cambridge Core.
  23. ^ Honsberger, Ross (1995), "Chapter 10. The Brocard Points", Episodes in Nineteenth and Twentieth Century Euclidean Geometry, Washington, D.C.: The Mathematical Association of America
  24. ^ Weisstein, Eric W. "Brocard Points". MathWorld--A Wolfram Web Resource. MathWorld. Retrieved 11 January 2022.
  25. ^ Clark Kimberling (1994). "Central Points and Central Lines in the Plane of a Triangle". Mathematics Magazine. 67 (3): 163–187. doi:10.1080/0025570X.1994.11996210. Retrieved 10 January 2022.
  26. ^ Weisstein, Eric W. "Central Line". From MathWorld--A Wolfram Web Resource. Retrieved 10 January 2022.
  27. ^ Kimberling, Clark. "Glossary : Encyclopedia of Triangle Centers". Archived from the original on 23 April 2012. Retrieved 10 January 2022.
  28. ^ "Triangle Conics". WolframMathWorld. Wolfram Research, Inc. Retrieved 11 November 2021.
  29. ^ Adrian Oldknow (July 1995). "Computer Aided Research into Triangle Geometry". The Mathematical Gazette. 79 (485): 263–274. doi:10.2307/3618298. JSTOR 3618298.
  30. ^ Sava Grozdev and Deko Dekov (November 2015). "A Survey of Mathematics Discovered by Computers" (PDF). International Journal of Computer Discovered Mathematics: 3–20. Retrieved 12 January 2022.
  31. ^ Sava Grozdev, Hiroshi Okumura, Deko Dekov. "Computer Discovered Encyclopedia of Euclidean Geometry". Computer Discovered Encyclopedia of Euclidean Geometry. Sava Grozdev, Hiroshi Okumura, Deko Dekov. Retrieved 12 January 2022.{{cite web}}: CS1 maint: 여러 이름: 작성자 목록(링크)

추가 판독치