기하학에서, 원곡선의 삼각형 ABC와 점 P가 주어진다면, AB, AC, BC 선에서 P에 가장 가까운 점 3개는 공선이다.^[1]이 점들을 통과하는 선은 로버트 심슨의 이름을 딴 P의 심슨 선이다.^[2]그러나 이 개념은 1799년 윌리엄 월리스에 의해 처음 출판되었다.^[3]

그 반대도 사실인데, 만약 세 줄의 P에 가장 가까운 세 개의 점이 공선이고, 두 줄의 선이 평행하지 않으면, P는 세 줄에 의해 형성된 삼각형의 원곡선 위에 놓여 있다.또는 다시 말하면, 삼각형 ABC와 점 P의 심슨 선은 직선으로 전락한 ABC와 P의 페달 삼각형일 뿐이며, 이 조건은 P의 위치를 구속하여 삼각형 ABC의 원을 추적한다.

방정식

복잡한 평면에 삼각형을 배치하고, 원주 단위가 있는 삼각형 ABC에 정점을 두도록 하며, 그 위치에는 복잡한 좌표 a, b, c가 있고, 복잡한 좌표가 있는 P가 원주 단위의 점이 되게 한다.심슨 라인은 만족스러운^{[4]: Proposition 4} 점들의 집합이다.

${\displaystyle 2abc{\z}-2pz+p^{2}+(a+b+c)p-(bc+ca+ab)-{\frac {p}{p}=0,}$

여기서 돌출부는 복잡한 결합을 나타낸다.

특성.

• 삼각형의 꼭지점의 심슨 선은 그 꼭지점에서 떨어진 삼각형의 고도로, 정점 반대편의 점의 심슨 선은 그 꼭지점 반대편의 삼각형의 면이다.
• P와 Q가 원주의 점인 경우, P와 Q의 심슨 선 사이의 각도는 호 PQ의 각도의 절반이다.특히 점이 정반대인 경우 심슨 선은 수직이며 이 경우 선의 교차점은 9점 원 위에 있다.
• H가 삼각형 ABC의 직각점을 나타내도록 하면, P의 심슨 선은 9점 원 위에 놓여 있는 점으로 세그먼트 PH를 이등분한다.
• 동일한 원을 가진 두 개의 삼각형이 주어진 경우, 두 삼각형에 대한 원주에 대한 점 P의 심슨 선 사이의 각도는 P에 의존하지 않는다.
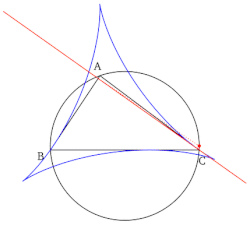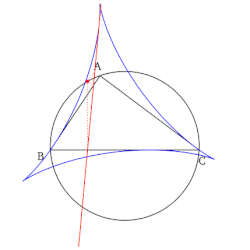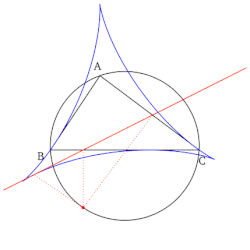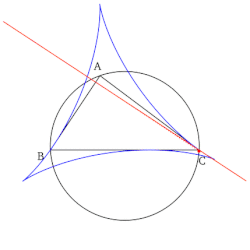
• 모든 심슨 선들의 집합은 그릴 때 기준 삼각형의 슈타이너 델토이드라고 알려진 델토이드 모양으로 봉투를 형성한다.
• 기준 삼각형의 한 측면(위의 첫 번째 속성 참조)과 일치하는 심슨 선의 구조는 이 측면 라인에 비견점을 산출한다.이 점은 건설되고 있는 측선의 중간점에 대한 고도(측선으로 투하)의 발의 반영이다.더욱이 이 점은 기준 삼각형의 측면과 그것의 스테이너 델토이드 사이의 접선점이다.
• 평행이 아닌 사각형은 심슨 포인트라고 불리는 하나의 페달 포인트를 가지고 있는데, 심슨 포인트라고 불리는 4각형의 발이 시린이다.^[5]사다리꼴의 심슨 점은 두 개의 비병렬 변의 교차점이다.^{[6]: p. 186}
• 적어도 5개의 면이 있는 볼록한 폴리곤은 심슨 선을 가지고 있지 않다.^[7]

존재 증명

The method of proof is to show that ${\displaystyle \angle NMP+\angle PML=180^{\circ }}$. ${\displaystyle PCAB}$ is a cyclic quadrilateral, so ${\displaystyle \angle PBA+\angle ACP=\angle PBN+\angle ACP=180^{\circ }}$. ${\displayst$$yle PMNB}$ is a cyclic quadrilateral (Thales' theorem), so ${\displaystyle \angle PBN+\angle NMP=180^{\circ }}$. Hence ${\displaystyle \angle NMP=\angle ACP}$. Now ${\displaystyle PLCM}$ is cyclic, so ${\displaystyle \angle PML=\a$$ngle PCL=180^{\circ }-\angle ACP}$. Therefore ${\displaystyle \angle NMP+\angle PML=\angle ACP+(180^{\circ }-\angle ACP)=180^{\circ }}$.

대체 증명

인접한 그림에서 점 Z가 무엇이든 + c는 90이다.또한, Z가 어떤 점이든, c와 b는 같아질 것이다.그러므로 우리는 다음과 같은 것을 가지고 있다.

a + c = 90

∴ a + b = 90 …(c와 b는 같음)(1)

이제 각도의 측정을 고려하십시오: a + 90 + b.

이 각도가 180이라는 것을 보여주면 심슨의 정리가 증명된다.

(1)부터 + 90 + b = 180

Q.E.D.

일반화

일반화 1

• ABC를 삼각형으로 하고, ℓ 선은 원곡선 O를 통과하게 하고, P점은 원곡선 위에 놓이게 한다.AP, BP, CP는 각각 A_p, B_p, C에서_p ℓ을 만나도록 한다.A₀, B₀, C를₀ 각각 BC, CA, AB에 대한 A_p, B_p, C의_p 투영으로 한다.그러면 A₀, B₀, C는₀ 공선이다.더욱이, 새로운 선은 PH의 중간점을 통과하며, 여기서 H는 ΔABC의 직교점이다.ℓ이 P를 통과하면 심슨 라인과 선이 일치한다.^[8][9][10]

일반화 2

• 삼각형 ABC의 정점을 원뿔 Ⅱ에 놓고 Q, P를 평면에서 두 점으로 한다.PA, PB, PC가 각각 A₁, B, C에서₁₁ 원뿔을 교차하도록 한다.QA는₁ A에서₂ BC를 교차하고, QB는₁₂ B에서 AC를 교차하며₁, QC는₂ C에서 AB를 교차한다.그 다음, Q가 원뿔 Ⅱ에 놓여 있을 경우에만₂ A₂, B, C₂, P 4점이 시준된다.^[11]

일반화 3

• R. F. 사이스터는 주기 4각형의 심슨 선에서 주기 4각 측정에 대한 정리를 일반화했다.

참고 항목

• 페달 삼각형
• 로버트 심슨

참조

외부 링크

위키미디어 커먼즈에는 심슨 라인과 관련된 미디어가 있다.

• 심슨 라인 cut-the-knot.org
• F. M. 잭슨과
• Neuberg의 정리 및 심슨-월러스 라인의 일반화, 대화형 동적 기하학적 스케치.