경사면

Inclined plane
"램프"는 여기서 리다이렉트 됩니다.다른 용도는 램프(동음이의)를 참조하십시오.
이 기사는 물리적 구조에 대한 것입니다.다른 용도는 기울어진 평면(동음이의)을 참조하십시오.
프랑스 샤르트르, 몽테스코 호텔, 휠체어 램프
교육에 사용되는 시연용 경사면, 플로렌스 갈릴레오 박물관.

경사로라고도 알려진 경사면은 한쪽 끝이 다른 쪽보다 높게 기울어진 평평한 지지면이며,[1][2][3] 하중을 올리거나 내리기 위한 보조 도구로 사용됩니다.기울어진 평면은 르네상스 과학자들에 의해 정의된 6개의 고전적인 단순 기계들 중 하나이다.경사면은 수직 장애물 위로 무거운 하중을 이동시키는 데 사용됩니다.예를 들어 트럭에 물건을 싣는 데 사용되는 경사로에서부터 보행로를 [3]걸어 올라가는 사람, 언덕을 오르는 자동차나 철도 열차에 이르기까지 다양하다.

물체를 경사면 위로 이동시키는 것은 이동 [4]거리가 늘어나지만 똑바로 위로 들어올리는 것보다 힘이 덜 든다.힘이 감소하는 요소인 경사면의 기계적 이점은 경사면이 가로지르는 높이에 대한 경사면의 길이 비율과 같다.에너지의 보존에 의해, 마찰에 의한 손실을 무시하고, 주어진 수직 거리만큼 물체를 들어올리는 데 같은 양의 기계적 에너지(작업)가 필요하지만, 경사면은 더 [5][6]먼 거리에 가해지는 더 작은 힘으로 동일한 작업을 수행할 수 있다.

때때로 [7]정지각이라고도 불리는 [8]마찰각은 하중이 미끄러지지 않고 마찰로 인해 경사면에서 움직이지 않고 쉴 수 있는 최대 각도입니다.이 각도는 [8]표면 사이의 정적 마찰계수s μ의 아크탄젠트와 같다.

다른 두 개의 단순한 기계는 종종 경사면에서 [9]파생된 것으로 간주된다.쐐기는 움직이는 경사면 또는 [5]베이스에 연결된 두 개의 경사면으로 간주할 수 있다.나사는 실린더를 [5]감싼 좁은 경사면으로 구성됩니다.

이 용어는 또한 특정 구현을 나타낼 수도 있습니다. 즉, 언덕 위 및 아래쪽으로 물품을 운송하기 위해 가파른 언덕에 직선 경사로가 잘려 있습니다.여기에는 레일 위 또는 케이블 시스템에 의해 견인된 차량, Johnstown 경사면 같은 기능성 또는 케이블 철도가 포함될 수 있습니다.

사용하다

경사면은 트럭, 선박, 비행기에 [3]화물을 싣고 내리는 경사로의 형태로 널리 사용된다.휠체어 램프는 휠체어를 탄 사람들이 자신의 힘을 초과하지 않고 수직 장애물을 극복할 수 있도록 하기 위해 사용됩니다.에스컬레이터와 경사 컨베이어 벨트도 경사면의 [6]한 형태입니다.케이블 또는 케이블 철도에서 철도 차량은 케이블을 사용하여 가파른 경사면을 끌어올린다.경사면은 또한 사람을 포함한 무겁고 연약한 물체를 중력을 줄이기 위해 비행기의 정상적인 힘을 사용하여 수직 거리 아래로 안전하게 내려갈 수 있게 해준다.항공기 대피 슬라이드는 사람들이 여객기의 높이에서 빠르고 안전하게 지상에 도달할 수 있게 해준다.

트럭에 차를 싣기 위해 경사로 사용
경사로를 이용한 화물차 적재
항공기 비상 대피 슬라이드
일본 버스의 휠체어 램프
트럭에 램프 적재

다른 경사면은 영구 구조물에 내장됩니다.차량 및 철도용 도로는 차량이 [3]노면의 트랙션을 잃지 않고 언덕과 같은 수직 장애물을 극복할 수 있도록 완만한 경사면, 경사면, 둑길 형태의 경사면을 가지고 있다.마찬가지로, 보행로와 인도에는 보행자가 [1][4]트랙션을 유지할 수 있도록 경사를 제한하는 완만한 경사로가 있습니다.경사면은 또한 놀이터 미끄럼틀, 워터슬라이드, 스키 슬로프, 스케이트보드 공원 등에서 사람들이 통제된 방식으로 미끄러져 내리는 오락물로 사용된다.

서기 72년 이스라엘 마사다를 침략하기 위해 로마인이 건설한 어스 램프(오른쪽)
브라질리아 팔라시오 도 플라날토, 보행자 진입로
존스타운 경사면, 기능성 철도입니다.
버마 로드, 아삼, 인도, 버마를 거쳐 중국으로 1945년
스케이트보드 공원의 경사면


역사

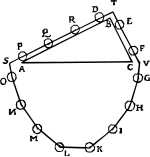
스테빈의 증거
StevinEquilibrium.svg
1586년, 플랑드르의 기술자 사이먼 스테빈은 [10]구슬의 줄을 사용한 논쟁으로 경사면의 기계적 이점을 이끌어냈다.그는 프리즘처럼 등 뒤로(위) 배치된 높이가 같지만 경사가 다른 두 개의 경사면을 상상했다.같은 간격으로 구슬이 달린 끈의 고리가 경사면 위에 드리워져 있고, 끈의 일부가 아래에 매달려 있다.평면에 놓여 있는 구슬은 T 지점에서 끈의 장력에 의해 지탱되는 평면의 하중으로 작용합니다.Stevin의 주장은 [10][11][12]다음과 같습니다.
  • 문자열은 정적 평형 상태에서 정지 상태여야 합니다.현이 다른 쪽보다 무거워져 자신의 무게로 오른쪽 또는 왼쪽으로 미끄러지기 시작하면 각 비드가 이전 비드의 위치로 이동했을 때 현은 초기 위치와 구별할 수 없게 되므로 균형이 맞지 않고 계속 미끄러집니다.이 주장은 무한정 반복될 수 있고, 결과적으로 순환 영구 운동으로 이어질 수 있는데, 이는 터무니 없다.따라서, T점(위)에 있는 양쪽의 힘이 같은 상태에서 정지해 있습니다.
  • 기울어진 평면 아래에 매달려 있는 체인의 부분은 대칭이며, 양쪽에 같은 수의 구슬이 있습니다.그것은 현의 양쪽에 동일한 힘을 가한다.따라서 줄의 이 부분은 평면의 가장자리(점 S 및 V)에서 절단할 수 있으며, 비즈만 경사면에 놓여 있고 나머지 부분은 여전히 정적 평형 상태에 있습니다.
  • 구슬은 끈에서 동일한 간격으로 이루어지기 때문에 각 평면에서 지원되는 구슬의 총 수, 즉 총 하중은 평면의 길이에 비례합니다.입력 지지력, 스트링의 장력은 양쪽에서 동일하기 때문에 각 평면의 기계적 이점은 경사 길이에 비례합니다.

Dijksterhuis가 [13]지적했듯이 Stevin의 주장은 완전히 엄격하지 않다.체인의 매달린 부분이 가해지는 힘은 놓았을 때 모양을 유지할 필요가 없기 때문에 대칭적일 필요가 없다.비록 체인이 0의 각운동량으로 방출되더라도, 체인이 처음에 평형구성에 있지 않는 한 진동을 포함한 운동이 가능하며, 이는 인수를 원형으로 만들 것이다.

경사면은 선사시대부터 무거운 물체를 [14][15]이동시키기 위해 사람들에 의해 사용되어 왔다.로마와 같은 고대 문명이 건설한 경사진 도로와 둑길은 살아남은 초기 경사면의 사례로, 그들이 물건을 위로 옮기는 데 있어 이 장치의 가치를 이해했음을 보여준다.스톤헨지와[16] 같은 고대 석조 건축물에 사용된 무거운 돌들은 [17]흙으로 만들어진 경사면을 이용해 옮겨져 제자리에 놓여진 것으로 추정되지만, 이러한 임시 건물 경사로의 증거는 찾기 어렵다.이집트 피라미드는 경사면을 [18][19][20]이용해 지어졌고, 공성전은 고대 군대가 요새 벽을 넘을 수 있게 했다.고대 그리스인들은 [4]코린트 지협을 가로질러 육로로 배를 끌기 위해 6킬로미터 (3.7마일) 길이의 포장된 경사로인 디올코스를 건설했다.

그러나 경사면은 기계로 인식되는 6개의 전형적인 단순 기계 중 마지막이었다.이는 수동적이고 움직임이 없는 장치(하중은 움직이는 부분)[21]이며 자연에서 경사면이나 언덕의 형태로 발견되기 때문일 것입니다.비록 그들은 무거운 물체를 들어올리는 데 그것이 사용되는 것을 이해했지만, 다른 다섯 개의 간단한 기계를 정의한 고대 그리스 철학자들은 기울어진 평면을 [22]기계로 포함하지 않았다.1826년 칼 폰 랑스도르프는 기울어진 평면이 산의 경사면보다 더 이상 기계가 아니라고 썼다.[21]기울어진 평면을 위로 추를 밀어 올리는 데 필요한 힘(기계적 이점)을 계산하는 문제는 그리스 철학자 알렉산드리아의 헤론(기원전 10 - 60)과 알렉산드리아의 파푸스(기원전 290 - 350)에 의해 시도되었지만,[23][24][25] 그들의 해결책은 정확하지 않았다.

르네상스 시대에 이르러서야 기울어진 평면이 수학적으로 풀리고 다른 간단한 기계들과 분류되었다.기울어진 평면의 첫 번째 정확한 분석은 13세기 작가 조르나스 드 네모어의 [26][27]작품에서 나타났지만, 그의 해법은 분명히 [24]그 시대의 다른 철학자들에게 전달되지 않았다.지롤라모 카르다노(1570)는 입력력이 [10]평면의 각도에 비례한다는 잘못된 해법을 제안했다.그리고 나서 16세기 말에, 10년 안에 세 개의 정답이 마이클 바로, 사이먼 스테빈, 갈릴레오 갈릴레이에 의해 출판되었다.[24]최초의 것은 아니지만, 플라망어 엔지니어 사이먼 스테빈의[25] 유래가 가장 잘 알려져 있는데, 그 독창성과 구슬의 줄 사용 때문이다(상자 [12][26]참조).1600년, 이탈리아 과학자 갈릴레오 갈릴레이는 르 메카니케의 간단한 기계 분석에 경사면을 포함시켰고, 이것은 힘의 [28]증폭기로서 다른 기계들과 기본적인 유사성을 보여주었다.

경사면에서 미끄럼 마찰의 첫 번째 기본 법칙은 레오나르도 다빈치 (1452-1519)에 의해 발견되었지만 그의 노트에 [29]발표되지 않았다.그것들은 기욤 아몬통 (1699년)에 의해 재발견되었고 샤를 오귀스틴 드 쿨롱 (1785년)[29]에 의해 더욱 개발되었다.레온하르트 오일러(1750)는 경사면에서 정지각의 접선이 [30]마찰계수와 같다는 것을 보여주었다.

용어.

경사

기울어진 평면의 기계적 이점은 기울기 또는 경사를 의미하는 기울기에 따라 달라집니다.경사가 작을수록 기계적 이점이 커지고 주어진 무게를 올리는 데 필요한 힘이 작아집니다.평면의 기울기 s는 수평 길이로 나눈 양 끝 사이의 높이 차이 또는 "상승" 또는 "실행"[31]과 같습니다.또한 평면이 수평으로 만드는 각도인 θ로 표현할 수 있다.

기울어진 평면의 형상은 직각 [31]삼각형을 기준으로 합니다.수평 길이는 높이 상승의 수직 변화인 계단진행이라고도 합니다.

기계적 이점

단순 기계의 기계적 이점 MA는 부하에 가해지는 입력력에 대한 출력력의 비율로 정의됩니다.기울어진 평면에서 출력 하중력은 평면에 있는 하중 물체의 중력(중량w F)일 뿐이다.입력력은 평면에 평행하게 물체를 위로 이동시키기 위해 물체에 가해지는 힘 F입니다i.기계적인 장점은

마찰이 없는 이상적인 경사면의 MA는 때때로 IMA(Ideal Mechanical Advantage)라고 불리는 반면 마찰이 포함된 MA는 실제 기계적 어드밴티지([32]AMA)라고 불립니다.

무마찰 경사면

1900년경 물리학 교육에 사용된 계기 경사면.왼쪽 무게에 의해 하중w F가 제공됩니다.8중량은 롤러를 평면으로 끌어올리는 입력력i F를 제공합니다.

움직이는 물체와 평면 사이에 마찰이 없다면 이 장치를 이상적인 경사면이라고 한다.이 상태는 물체가 배럴처럼 굴러가거나 바퀴나 바퀴로 지지되는 경우 접근할 수 있습니다.에너지 보존으로 인해 마찰이 없는 경사면의 경우 하중 리프팅 작업out W는 입력력 W에in[33][34][35] 의해 수행되는 작업과 동일합니다.

일은 물체가 움직이는 변위에 힘을 곱한 것으로 정의된다.하중에 가해지는 작업은 하중이 상승하는 수직 변위에 곱한 것과 같으며, 이는 경사면의 "상승"입니다.

입력 작업은 물체에 가해지는 힘i F에 경사면의 대각선 길이를 곱한 것과 같다.

위의 에너지 방정식의 보존에 이러한 값을 대입하여 재배치한다.

평면의 [34]각도 θ로 기계적 이점을 표현하기 위해 그림(위)에서 볼 수 있다.

그렇게

따라서 마찰이 없는 경사면의 기계적 이점은 경사각의 사인 역수와 같습니다.이 방정식의 입력력i F는 하중을 경사면에서 움직이지 않게 유지하거나 일정한 속도로 밀어 올리는 데 필요한 힘이다.입력력이 이보다 크면 부하가 평면을 가속합니다.힘이 더 작으면 비행기에서 가속됩니다.

마찰이 있는 경사면

예를 들어 무거운 박스가 램프 위로 미끄러지는 등 평면과 하중 사이에 마찰이 있는 경우에는 입력력에 의해 가해지는 일부 워크가 마찰에fric 의해 열로 방산되므로 부하에 대한 작업이 감소한다.에너지 절약으로 인해 출력 작업과 마찰 에너지 손실의 합계는 입력 작업과 동일합니다.

따라서 마찰이 없는 경우보다 더 많은 입력력이 필요하고 기계적 이점이 낮습니다.마찰 시 하중은 표면에 평행한 순력이 반대되는 [8][36][37]마찰력f F보다 클 경우에만 이동합니다.최대 마찰력은 다음과 같습니다.

여기서n F는 하중과 평면 사이의 정상적인 힘이며 표면으로 향하는 수직 방향이고 μ는 재료에 따라 달라지는 두 표면 사이의 정적 마찰 계수이다.입력력이 가해지지 않을 때 평면의 기울기 각도 θ가 최대값 θ보다 작을 경우 평면에 평행한 중력의 성분은 마찰을 극복하기에 너무 작아 하중이 움직이지 않게 된다.이 각도를 정지각이라고 하며 표면의 구성에 따라 다르지만 하중 무게와는 무관합니다.정지각θ의 탄젠트가 μ인 것을 아래에 나타냅니다.

마찰의 경우, 하중이 평면을 위아래로 미끄러지지 않고 정지해 있는i 입력력 F의 범위가 항상 존재하지만, 무마찰 경사면의 경우 하중이 정지해 있는 입력력의 특정 값은 1개뿐입니다.

분석.

키n: F = N = 평면에 수직인 수직력, Fi = f = 입력력, Fw = mg = 하중 중량, 여기서 m = 질량, g = 중력

자유체로 간주될 때 경사면에 놓인 하중은 다음과 같은 세 가지 힘이 [8][36][37]작용한다.

  • 하중을 이동시키기 위해 가해지는 힘, F는i 경사면과 평행하게 작용한다.
  • 수직 하방으로 작용하는 하중 F의w 무게
  • 부하에 대한 평면의 힘.이 문제는 다음 두 가지 컴포넌트로 해결할 수 있습니다.
    • 하중을 지탱하는 경사면의 수직력n F.이 방향은 지표면에 수직(정규)입니다.
    • 하중에서 평면의 마찰력 F는f 표면과 평행하게 작용하며 항상 물체의 움직임과 반대 방향으로 작용한다.이는 두 표면 사이의 정적 마찰계수 μ를 곱한 정상력과 같다.

뉴턴의 두 번째 운동 법칙을 사용하면 하중은 정지하거나, 힘의 합계가 0일 경우 일정한 운동을 하게 됩니다.오르막과 내리막 운동의 경우 마찰력의 방향이 반대이기 때문에, 이 두 가지 경우를 별도로 고려해야 한다.

  • 오르막 동작:하중에 가해지는 총 힘은 오르막 쪽으로 향하기 때문에 마찰력은 입력력에 반대하여 평면을 따라 아래로 향합니다.
오르막 운동에 대한 기계적 이점 도출

평면에 평행하고 수직인 힘에 대한 평형 방정식은 다음과 같다.

f n (\{f}=\ F_를 첫 번째 방정식으로 대체
번째 방정식을 F n w cos ⁡ { n}= \theta 를 구하여 위의 방정식으로 대체한다.
tan \ = \
분모의 삼각함수 항등식을 사용하여
기계적인 장점은
여기서 tan - {\ =\^{- 이는 경사면 위로 임박한 움직임을 위한 조건이다.가해진 힘i F가 이 방정식에 의해 주어진 것보다 클 경우, 하중은 평면을 위로 이동합니다.
  • 내리막 운동:하중에 가해지는 총력은 내리막 쪽이기 때문에 마찰력은 평면 위로 향합니다.
내리막 운동에 대한 기계적 이점 도출

평형 방정식은

f n (\{f}=\ F_를 첫 번째 방정식으로 대체
번째 방정식을 F n w cos ⁡ { n}= \theta 를 구하여 위의 방정식으로 대체한다.
tan { displaystyle = \}로 대체하고 위와 같이 단순화
분모에 다른 삼각 항등식을 사용하면
기계적인 장점은
이것은 평면을 내려가는 임박한 움직임을 위한 조건입니다. 가해진 힘i F가 이 방정식에서 주어진 것보다 작을 경우 하중은 평면을 따라 미끄러집니다.세 가지 경우가 있습니다.
  1. 은 마이너스입니다힘이 가해지지 않으면 하중은 움직이지 않고 아래로 미끄러지려면 약간의 음의 힘을 가해야 합니다.
  2. = displaydisplay （ \ \theta = \ : '안식의 각도'입니다.기계적 이점은 무한합니다.힘을 가하지 않으면 하중은 미끄러지지 않지만 약간의 음의 힘(하강)만 가해도 미끄러집니다.
  3. \ \theta > \힘이 가해지지 않을 경우 하중은 평면을 따라 미끄러져 내려가고, 하중을 움직이지 않게 유지하려면 일정한 양의 (상행) 힘이 필요합니다.

전력을 이용한 기계적 이점

키 : N = 평면에 수직인 수직력 W = mg (여기서 m = 질량, g = 중력, θ (theta) = 평면의 기울기 각도)

경사면의 기계적 이점은 경사면을 위로 끌어올리는 데 필요한 힘에 대한 경사면의 하중 비율입니다.에너지가 분산되거나 부하 이동에 저장되지 않는 경우, 이 기계적 이점은 램프의 치수를 통해 계산할 수 있습니다.

이를 나타내기 위해, 수평 위의 각도 θ를 가진 램프를 따라 달리는 철도 차량의 위치 r이 다음과 같이 지정되도록 합니다.

여기서 R은 램프를 따른 거리입니다.경사로 위로 올라오는 차의 속도는

손실이 없기 때문에 부하를 램프 위로 이동시키기 위해 힘 F에 의해 사용되는 전력은 전원 출력과 같으며, 이는 부하 중량 W의 수직 상승입니다.

차량을 램프 위로 끌어올리는 입력 전력은 다음과 같습니다.

그리고 전원 차단은

전원 투입과 전원 투입을 동일시하여 다음과 같은 기계적 이점을 얻습니다.

경사면의 기계적 이점은 램프 각도의 사인 값이 다음과 같이 주어지기 때문에 램프 L의 높이 H에 대한 길이 비율에서 계산할 수도 있습니다.

그러므로,

리버풀 Minard 경사면의 케이블 드라이브 시스템 레이아웃.

예:램프의 높이가 H = 1m이고 길이가 L = 5m인 경우 기계적 이점은 다음과 같습니다.

즉, 20파운드 힘이 100파운드 하중을 들어올린다는 뜻입니다.

리버풀 미나드 경사 비행기는 1804m x 37.50m의 치수를 가지고 있으며, 이것은 다음과 같은 기계적 이점을 제공한다.

따라서 케이블에 100파운드 장력이 가해지면 4810파운드 하중이 상승합니다.이 경사의 기울기는 2%로, 각도 θ가 sin = tan θ에 충분히 작다는 것을 의미합니다.

「 」를 참조해 주세요.

레퍼런스

  1. ^ a b Cole, Matthew (2005). Explore science, 2nd Ed. Pearson Education. p. 178. ISBN 978-981-06-2002-8.
  2. ^ Merriam-Webster's collegiate dictionary, 11th Ed. Merriam-Webster. 2003. pp. 629. ISBN 978-0-87779-809-5. inclined plane definition dictionary.
  3. ^ a b c d "The Inclined Plane". Math and science activity center. Edinformatics. 1999. Retrieved March 11, 2012.
  4. ^ a b c Silverman, Buffy (2009). Simple Machines: Forces in Action, 4th Ed. USA: Heinemann-Raintree Classroom. p. 7. ISBN 978-1-4329-2317-4.
  5. ^ a b c Ortleb, Edward P.; Richard Cadice (1993). Machines and Work. Lorenz Educational Press. pp. iv. ISBN 978-1-55863-060-4.
  6. ^ a b Reilly, Travis (November 24, 2011). "Lesson 04:Slide Right on By Using an Inclined Plane". Teach Engineering. College of Engineering, Univ. of Colorado at Boulder. Archived from the original on May 8, 2012. Retrieved September 8, 2012.
  7. ^ Scott, John S. (1993). Dictionary of Civil Engineering. Chapman & Hill. p. 14. ISBN 978-0-412-98421-1. angle of friction [mech.] in the study of bodies sliding on plane surfaces, the angle between the perpendicular to the surface and the resultant force (between the body and the surface) when the body begins to slide. angle of repose [s.m.] for any given granular material the steepest angle to the horizontal at which a heaped surface will stand in stated conditions.
  8. ^ a b c d Ambekar, A. G. (2007). Mechanism and Machine Theory. PHI Learning. p. 446. ISBN 978-81-203-3134-1. Angle of repose is the limiting angle of inclination of a plane when a body, placed on the inclined plane, just starts sliding down the plane.
  9. ^ Rosen, Joe; Lisa Quinn Gothard (2009). Encyclopedia of Physical Science, Volume 1. Infobase Publishing. p. 375. ISBN 978-0-8160-7011-4.
  10. ^ a b c Koetsier, Teun (2010). "Simon Stevin and the rise of Archimedean mechanics in the Renaissance". The Genius of Archimedes – 23 Centuries of Influence on Mathematics, Science and Engineering: Proceedings of an International Conference Held at Syracuse, Italy, June 8–10, 2010. Springer. pp. 94–99. ISBN 978-90-481-9090-4.
  11. ^ Devreese, Jozef T.; Guido Vanden Berghe (2008). 'Magic is no magic': The wonderful world of Simon Stevin. WIT Press. pp. 136–139. ISBN 978-1-84564-391-1.
  12. ^ a b Feynman, Richard P.; Robert B. Leighton; Matthew Sands (1963). The Feynman Lectures on Physics, Vol. I. USA: California Inst. of Technology. pp. 4.4–4.5. ISBN 978-0-465-02493-3.
  13. ^ E.J.Dijksterhuis:사이먼 스테빈 1943
  14. ^ Therese McGuire, Light on Sacred Stones, in Conn, Marie A.; Therese Benedict McGuire (2007). Not etched in stone: essays on ritual memory, soul, and society. University Press of America. p. 23. ISBN 978-0-7618-3702-2.
  15. ^ Dutch, Steven (1999). "Pre-Greek Accomplishments". Legacy of the Ancient World. Prof. Steve Dutch's page, Univ. of Wisconsin at Green Bay. Retrieved March 13, 2012.
  16. ^ Moffett, Marian; Michael W. Fazio; Lawrence Wodehouse (2003). A world history of architecture. Laurence King Publishing. p. 9. ISBN 978-1-85669-371-4.
  17. ^ Peet, T. Eric (2006). Rough Stone Monuments and Their Builders. Echo Library. pp. 11–12. ISBN 978-1-4068-2203-8.
  18. ^ Thomas, Burke (2005). "Transport and the Inclined Plane". Construction of the Giza Pyramids. world-mysteries.com. Retrieved March 10, 2012.
  19. ^ Isler, Martin (2001). Sticks, stones, and shadows: building the Egyptian pyramids. USA: University of Oklahoma Press. pp. 211–216. ISBN 978-0-8061-3342-3.
  20. ^ Sprague de Camp, L. (1990). The Ancient Engineers. USA: Barnes & Noble. p. 43. ISBN 978-0-88029-456-0.
  21. ^ a b 칼 폰 랑스도르프(1826) 마치넨쿤데, 인용문:
  22. ^ 예를 들어, 로마 건축가 비트루비우스(기원전 80–15년)와 그리스 철학자 알렉산드리아의 헤론(기원전 10–70년)이 남긴 단순 기계 목록은 기울어진 평면을 제외한 다섯 개의 고전적인 단순 기계로 구성되어 있다.–Smith, William (1848). Dictionary of Greek and Roman antiquities. London: Walton and Maberly; John Murray. p. 722. ,
  23. ^ Heath, Thomas Little (1921). A History of Greek Mathematics, Vol. 2. UK: The Clarendon Press. pp. 349, 433–434.
  24. ^ a b c 이지디오 페스타와 소피 루, 경사진 평면의 수수께끼
  25. ^ a b Meli, Domenico Bertoloni (2006). Thinking With Objects: The Transformation of Mechanics in the Seventeenth Century. JHU Press. pp. 35–39. ISBN 978-0-8018-8426-9.
  26. ^ a b Boyer, Carl B.; Uta C. Merzbach (2010). A History of Mathematics, 3rd Ed. John Wiley and Sons. ISBN 978-0-470-63056-3.
  27. ^ Usher, Abbott Payson (1988). A History of Mechanical Inventions. Courier Dover Publications. p. 106. ISBN 978-0-486-25593-4.
  28. ^ Machamer, Peter K. (1998). The Cambridge Companion to Galileo. London: Cambridge University Press. pp. 47–48. ISBN 978-0-521-58841-6.
  29. ^ a b Armstrong-Hélouvry, Brian (1991). Control of machines with friction. USA: Springer. p. 10. ISBN 978-0-7923-9133-3.
  30. ^ Meyer, Ernst (2002). Nanoscience: friction and rheology on the nanometer scale. World Scientific. p. 7. ISBN 978-981-238-062-3.
  31. ^ a b Handley, Brett; David M. Marshall; Craig Coon (2011). Principles of Engineering. Cengage Learning. pp. 71–73. ISBN 978-1-4354-2836-2.
  32. ^ Dennis, Johnnie T. (2003). The Complete Idiot's Guide to Physics. Penguin. pp. 116–117. ISBN 978-1-59257-081-2.
  33. ^ Nave, Carl R. (2010). "The Incline". Hyperphysics. Dept. of Physics and Astronomy, Georgia State Univ. Retrieved September 8, 2012.
  34. ^ a b Martin, Lori (2010). "Lab Mech14:The Inclined Plane - A Simple Machine" (PDF). Science in Motion. Westminster College. Retrieved September 8, 2012.
  35. ^ Pearson (2009). Physics class 10 - The IIT Foundation Series. New Delhi: Pearson Education India. p. 69. ISBN 978-81-317-2843-7.
  36. ^ a b Bansal, R.K (2005). Engineering Mechanics and Strength of Materials. Laxmi Publications. pp. 165–167. ISBN 978-81-7008-094-7.
  37. ^ a b 이것은 모든 각도에서 가해지는 힘을 다루는 약간 더 일반적인 방정식을 도출한다.

외부 링크

Wikimedia Commons에는 기울어진 평면과 관련된 미디어가 있습니다.