음향탄성효과
Acoustoelastic effect음향탄성 효과는 초기 정적 응력장에 노출될 경우 탄성물질의 소리 속도(종방향 및 전단파 속도 모두)가 어떻게 변화하는지 의미한다.이것은 연속 질량의 재료에서 기계적 응력과 유한 변형률 사이의 구성 관계의 비선형 효과다.고전적인 선형탄성론에서 대부분의 탄성물질의 작은 변형은 적용된 응력과 그에 따른 변형률 사이의 선형관계로 설명할 수 있다.이 관계는 일반적으로 일반화된 후크의 법칙으로 알려져 있다.선형 탄성 이론은 2차 탄력 상수(: { 및 를 포함하며, 적용된 응력에 영향을 받지 않고 탄성 물질에서 일정한 종방향 및 전단 음속을 산출한다.반면에 음향탄성 효과는 적용된 응력과 그에 따른 변형률 사이의 구성관계(비선형 탄성 이론[1])의 고차 확장이 포함되며, 재료의 응력 상태에 따라 종방향 및 전단음속도를 산출한다.비압축 재료의 한계에서는 선형 탄성 이론의 음속도가 재현된다.
음향탄성 효과는 1925년 브릴루인에 의해 조사되었다.[2]그는 음향파의 전파 속도가 인가된 정수압에 비례하여 감소한다는 것을 발견했다.그러나 그의 이론의 결과는 음파가 충분히 큰 압력에서 번식을 멈추게 된다는 것이었다.이러한 역설적 효과는 나중에 탄성 매개변수가 압력에 영향을 받지 않는다는 잘못된 가정에 의해 발생한다는 것을 보여주었다.[3]
1937년 프랜시스 도미니크 무르나한은[4] 탄성 등방성 물질의 유한 변형을 포함하도록 선형 탄성 이론을 확장하는 수학적 이론을 제시했다.이 이론. 1953년 Huges과 켈리[5]자신들의 실험적인 일에 Polystyrene,를 포함한 여러 탄성 물질에 대하여 고차 탄성 상수에 수치를 설립하기 위해 Murnaghan의 이론을 이용 3third-order 탄성 상수 나는{나는\displaystyle}, m{m\displaystyle}이고, n은{n\displaystyle}을 포함했다. 아르곤mco 철, 그리고 Pyrex는 정수압과 단축압축의 영향을 받는다.
과대성 소재에 대한 비선형 탄성 이론
음향탄성 효과는 비선형 탄성물질의 유한변형의 영향이다.이것에 대한 현대적인 포괄적인 설명은 에서 찾을 수 있다.[1]이 책은 비선형 탄성 이론의 적용과 큰 탄성 변형이 가능한 고체 재료의 기계적 특성 분석을 다룬다.다결정탄성강과 같은 압축성 동위원소 과극성 물질에 대한 음향탄성 이론의 특별한 사례는 오그덴이 제시한 비선형 탄성 이론에서 재현되어 이 본문에서 보여주고 있다.[6][1]
구성 관계 – 과대성 재료(스트레스-스트레인 관계)
과대증성 재료는 임의의 기준 구성에 관한 현재 변형 상태에 의해서만 결정되고 객관적으로 결정되는 Cauchy 탄성 재료의 특별한 경우다. (변형에 대한 자세한 내용은 변형(기전) 및 유한 변형 페이지도 참조한다.그러나 스트레스에 의해 수행되는 작업은 변형이 가는 경로에 따라 달라질 수 있다.따라서 Cauchy 탄성 물질은 비보수적인 구조를 가지며, 스트레스는 스칼라 탄성 전위함수에서 도출될 수 없다.응력에 의해 수행된 작업이 변형 경로와 독립적으로 이루어지는 Cauchy 탄성 재료의 특별한 경우를 녹색 탄성 또는 과대 재생성 재료라고 한다.이러한 재료는 보수적이며 재료의 응력은 일반적으로 스트레인 에너지 밀도 함수로 알려진 스칼라 탄성 전위에 의해 유도될 수 있다.
스트레스와 스트레인 사이의 구성적 관계는 선택된 스트레스와 스트레인 형태에 기초하여 다른 형태로 표현될 수 있다.첫 번째 Piola-Kirchhoff 스트레스 텐서 P {\공칭 스트레스 텐서 T = {\ 압축성 초탄성 소재의 구성 방정식은 라그랑지안 그린 변형률( 의 관점에서 다음과 같이 표현할 수 있다.
여기서 은(는) 변형 구배 텐서이며, 두 번째 식에서는 텐서 지수 표기법에 아인슈타인 합계 규약을 사용한다. 은 과대증성 재료의 변형 에너지 밀도 함수로서, 우측에 기준 구성의 질량 밀도 0을 곱할 필요가 없으므로 단위 질량 당이 아닌 단위 체적 당으로 정의되었다.[1]
스칼라 변형률 에너지 밀도 함수 가 현재 변형률 의 Taylor 시리즈 확장에 의해 대략적으로 추정될 수 있다고 가정하면 다음과 같이 (지수 표기법으로) 표현할 수 있다
변형 에너지 함수가 0이어야 하며 재료가 변형되지 않은 상태일 때(: W j= 0)= 가 최소여야 한다는 제한사항을 적용하면 변형 에너지 함수에 상수 또는 선형 항이 없다는 것은 명백하며, 따라서 다음과 같다.
여기서 은(는) 2차 탄력모듈리의 4차 텐서인 반면, k 은 3차 탄력모듈리의 6차 텐서인 것이다. = i 의 대칭 스칼라 변형률 에너지 밀도 W 와 함께 두 번째 순서 i i {\는 다음과 같은 대칭을 가지고 있음을 암시한다.
독립 탄성 상수의 수를 81개에서 36개로 줄인다.또한, 전력 팽창은 2차 모듈리도 주요한 대칭을 가지고 있다는 것을 의미한다.
이는 독립 탄성 상수의 수를 21개로 더욱 감소시킨다.3번째 순서 탄성모듈리 C_{에도 동일한 인수를 사용할 수 있다또한 이러한 대칭은 Voigt 표기법(: C l= I displaystyle {ijkl}=C_{{})으로 탄성 모듈리를 표현할 수 있게 한다. 및 k = displaystyle} ).
변형 구배 텐서는 다음과 같이 구성 요소 형태로 표현할 수 있다.
여기서 i 은(는 변형된 구성에서 i {\ X_을(를) 조정하기 위한 참조 의 P 을(는)의 변위한 것이다(유한 변형률 이론 페이지의 그림 2 참조).구성 관계에 스트레인 에너지 기능의 전력 확장을 포함하며, 유한 스트레인 텐서 페이지 수율에 주어진 팽창으로 라그랑지안 스트레인 텐서 E 를 대체한다(참고, 아래 케이스 는 위의 사례와 비교하여 이 절에서 사용됨).유한 변형 페이지) 구성 방정식
어디에
더 높은 순서의 용어는 무시되었다[7][8](자세한 파생어는 참조).For referenceM by neglecting higher order terms in this expression reduce to which is a version of the generalised Hooke's law where j 는 스트레스의 척도인 반면, k /x l{\는 스트레인의 척도인 , {\는 이들 사이의 선형관계인 것이다.
음속
작은 동적(음향) 변형이 이미 정적으로 강조된 물질을 방해한다고 가정할 때 음향학적 효과는 더 큰 유한 변형에 겹쳐진 작은 변형에 대한 효과로 간주할 수 있다(소형 대형 이론이라고도 함).[8]주어진 물질적 포인트의 세 가지 상태를 정의해 봅시다.참조(스트레스되지 않음) 상태에서 점은 좌표 벡터 에 의해 정의되는 반면, 동일한 점은 처음 받는 정적 스트레스 상태(즉, 적용된 프리스트레스 영향 아래)에서 좌표 벡터 {\}}}가 지정된다.마지막으로, 작은 동적 장애(음향응력장) 아래의 재료 점이 좌표 벡터 을(를) 갖는다고 가정한다그런 다음 재료 지점의 총 변위(정적인 프리스트레스와 동적 음향 장애의 영향 하에서)는 변위 벡터로 설명할 수 있다.
어디에
가해진 프리스트에 의한 정적(래그랑지안) 초기 변위, 음향 장애에 의한 (에어리언) 변위 각각을 기술한다.이어서 추가적인 오일러 교란 (에 대한 Cauchy의 첫 번째 운동법(또는 선형 운동량의 균형)은 소량-대량 가정으로 가정하여 중간 라그랑지 변형 ( of u에 따라 도출할 수 있다.
holds. 일정한 신체 힘(즉, 중력)의 효과가 무시된 카우치 제1 운동 법칙의 라그랑지 형식을 사용하면 산출된다.
- 첨자/위첨자 "0"은 이 텍스트에서 스트레스 받지 않는 기준 상태를 나타내기 위해 사용되며, 점 변수는 변수의 파생 시간( )이며, {은는) Lagrangian 좌표계 에 대한 발산 연산자다..
운동법칙의 우측(시간 의존적 부분)은 다음과 같이 표현할 수 있다.
under the assumption that both the unstressed state and the initial deformation state are static and thus .
좌측(공간 종속 부분)의 경우 체인 규칙을 사용하고 변위 벡터 사이의 관계를 통해 변수를 변경하여 에 대한 공간 라그랑지안 부분파생물을 확장시킬 수 있다.
여기서 짧은 ,( 0 )u k(0 ) / x j{\가 사용되었다.그러므로
Assuming further that the static initial deformation (the pre-stressed state) is in equilibrium means that , and the law of motion can in combination with the constitutive equation given above be reduced to a linear relation (i.e. where higher order terms in ) between the static initial deformation and the additional dynamic disturbance 을[7](를) 그대로(자세한 파생어는 참조)
어디에
이 식은 선형파 방정식으로 인식된다.폼의 평면 파동 고려
where is a Lagrangian unit vector in the direction of propagation (i.e. parallel to the wave number normal to the wave front, ), is a unit vector referred to as the polarization vector (입자 움직임의 방향을 기술한다), 은 위상파 속도, {\}은 연속적으로 2배의 차이가 있는 함수(예: 사인파 함수)이다.이 평면 파형을 수율 위에 파생된 선형 파동 방정식에 삽입
여기서 는 음향 텐서로서 도입되며, 에[10] 따라 달라진다.
이 식을 전파 조건이라고 하며, 주어진 전파 n 에 대해 평면파에 해당하는 가능한 파형의 속도 및 양극화를 결정한다.파동 속도는 특성 방정식에[10] 의해 결정될 수 있다.
여기서 이(가) 결정 요인이고 이(가) ID 매트릭스다.
과대증 재료 ( 는 대칭이며, 고유값( ( 2은 따라서 실제 값이다.파동 속도도 실제가 되려면 고유값이 양수여야 한다.[1]이 경우 주어진 전파 방향 에 대해 상호 직교 실제 평면 파형이 3개 존재한다 음향 텐셔너의 두 가지 표현으로 보아 다음과 같은[10] 것이 분명하다.
그리고 불평등 i j l > 강력 타원성 도 함) 모든 비제로 벡터 N {N 및 {mbol에 대해 동종 평면파의 속도가 실제임을 보장한다.편광 = 은 입자 운동이 전파 방향과 평행하는 종파에 해당한다(압축파라고도 함). = 인 두 편극화는 입자 운동이 전파 방향과 직교하는 횡파에 해당한다(전단파라고도 한다).[10]
등방성 물질
등방성 재료의 탄성모듈리
For a second order isotropic tensor (i.e. a tensor having the same components in any coordinate system) like the Lagrangian strain tensor have the invariants where is the trace연산자, 및 q , 2, 따라서 등방성 물질의 변형 에너지 함수는 ()= ( q ), ,,3,} W로 표현할 수 있다.,2,ldots 또는 중첩 위치로서 다시[8] 쓸 수 있다.
여기서 ,, , B, 은 상수다.탄성 moduli 더 잘 라메 매개 변수로 알려진 그 상수 λ{\lambda\displaystyle}과μ{\displaystyle \mu}두번째 주문, 세번째 주문 탄성 moduli by,[11]지만에 내가, m해당하는 대체 있{\displays 소개되는 동안 A, B,{\displaystyle A, B}, C{C\displaystyle}.tyl 이(가) Murnaghan에 의해 소개되었다.[4]이것을[8] 스트레인 에너지 기능에 대한 일반적인 표현과 결합하면 분명히 알 수 있다.
where . Historically different selection of these third order elastic constants have been used, and some of the variations is shown in Table 1.
| 랜도 & 리프시츠 (1986)[11] | 투핀 & 번스타인 (1961년)[12] | 무르나한 (1951년)[4] | 블렌드 (1969년)[13] | 에린 & 수쿠비 (1974년)[14] | 표준 K 스타일 | |
|---|---|---|---|---|---|---|
강철의 예시 값
표 2와 표 3은 문헌에 제시된 일부 강철 유형에 대한 2차 및 3차 탄성 상수를 나타낸다.
| 라메 상수 | 투핀 & 번스타인 상수 | ||||
|---|---|---|---|---|---|
| 재료 | |||||
| 헤클라 37 (0.4)%C)[15] | |||||
| 헤클라 37 (0.6%C)[15] | |||||
| 헤클라 138A을[15] | |||||
| 렉스 535 니 강철[15] | |||||
| 헤클라 ATV 오스테나틱[15] | |||||
| 라메 상수 | 무르난 상수 | ||||
|---|---|---|---|---|---|
| 재료 | |||||
| 니켈-스틸 S/NVT | |||||
| 레일강 검체 1 | |||||
| 레일강 검체4[17] | |||||
등방성 과대역률 재료의 단축장력에 대한 음향탄성
A cuboidal sample of a compressible solid in an unstressed reference configuration can be expressed by the Cartesian coordinates , where the geometry is aligned with the Lagrangian coordinate system, and is the length기준 구성에서 큐보이드 측면의x 방향의 단축 장력에 큐빅을 적용하여 변형된 구성에서 재료 점의 좌표를 = , = = , = 3 .x_}=\}=\ _{이가) 길쭉한 느낌을 준다.
i - 방향으로.여기서 는 큐보이드 면 의 현재(형식) 길이와 현재 구성의 측면 길이 사이의 비율이 다음으로 표시됨을 나타낸다.
교장선생님이 기지개를 켠다고 한다.For an isotropic material this corresponds to a deformation without any rotation (See polar decomposition of the deformation gradient tensor where and the rotation ).이는 주 스트레칭 i 에 의한 스펙트럼 표현을 통해 설명될 수 있으며, 신장 e 에 의해 동등하게 설명될 수 있다
방향( > 0 의 단일 장력에 대해서는 }이 어느 정도 증가한다고 가정한다.If the lateral faces are free of traction (i.e. ) the lateral elongations and are limited to the range . For isotropic symmetry the l단자 연장(또는 수축)도 같아야 한다(: e = 범위는 총 측면 수축 범위( = e =- 1 비물리적)에 해당하며 측면 치수는 변경되지 않는다( = = 0 이론적으로 축 치수가 증가함에 따라 가로 치수의 증가에 해당하는 0보다 큰 값으로 범위가 확장될 수 있다는 점에 주목한다.그러나 이 성질을 나타내는 재료(보조재료라고 함)는 극히 적다.
음속확대
강한 타원성 조건( j m > 인 경우이 유지되며, 세 가지 직교 양극화 방향( 은 주어진 전파 방향 {\boldsymbol{에 대해 0이 아닌 실제 음속을 제공한다다음은 적용된 단색 장력, 전파 방향 및 양극화 벡터의 정형화된 집합의 one 선택에 대한 음속도를 도출한다.For a uniaxial tension applied in the -direction, and deriving the sound velocities for waves propagating orthogonally to the applied tension (e.g. in the -direction with propagation vector ), one selection직교 편광의 형태는
이 세가지 음속은
여기서 음속 의 첫 번째 인덱스 {ij}는 전파 방향(여기서 3 을 나타내고, 두 번째 j 은 선택된 양극화 방향(= 을 나타냄)을 나타냄)을 나타냄)을 나타낸다.s 전파 방향 – 즉, 종파 및 i 는 전파 방향과 직각인 입자 운동(예: 전단파)에 해당한다.
Expanding the relevant coefficients of the acoustic tensor, and substituting the second- and third-order elastic moduli and with their isotropic equivalents, and resp따라서, 음속은 다음과 같이 표현된다.
어디에
3차 탄성 상수의 효과와 관련된 음향탄성계수다.[18]
측정방법
음속, 보다 구체적으로 음속 변화를 측정할 수 있게 하기 위해 어떤 응력 상태에 따른 물질에서 해당 물질을 통해 전파되는 음향 신호의 속도를 측정할 수 있다.이를 위한 몇 가지 방법이 있지만 모두 음속의 두 가지 물리적 관계 중 하나를 사용한다.첫 번째 관계는 한 지점에서 다른 지점으로 신호를 전파하는 데 걸리는 시간(일반적으로 두 개의 음향 변환기 사이의 거리 또는 한 변환기에서 반사 표면까지의 거리의 두 배)과 관련이 있다.이를 흔히 "비행 시간"(TOF) 측정이라고 하며, 관계를 사용한다.
여기서 은 신호가 이동하는 거리이고 은 이 거리를 이동하는 데 걸리는 시간이다.두 번째 관계는 시간의 역, 즉 신호의 주파수와 관련이 있다.이곳의 관계는
여기서 은 신호의 주파수, 은 파장 길이.주파수를 측정량으로 사용한 측정에서는 n의 파형 길이가 신호가 공명하는 길이와 일치하는 음향 공진 현상을 사용한다.이 두 방법 모두 비행 시간에서와 같이 직접 측정하거나 또는 공명하는 시료의 물리적 범위에 걸쳐 일치하는 파장 수를 통해 간접적으로 측정하는 거리에 따라 달라진다.
초음파 시험 기법의 예
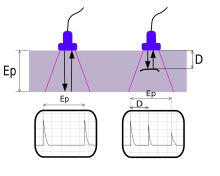
일반적으로 고체의 음속을 측정하기 위해 변환기 시스템을 설정하는 방법에는 두 가지가 있다.하나는 송신기 역할을 하는 반면 다른 하나는 수신기 역할을 하는 두 개 이상의 변환기를 가진 설정이다.그런 다음, 음향신호가 변환기 사이에서 이동한 거리를 알거나 측정한다고 가정하면서 송신기에서 신호가 생성되는 시간과 수신기에서 녹음되는 시간을 측정하거나, 또는 그 이상의 두께를 알고 있는 공명 주파수를 반대로 측정함으로써 음속 측정을 수행할 수 있다.물결이 울리다다른 형태의 설정은 흔히 맥박-에코 시스템이라고 불린다.여기에는 하나의 변환기가 송신기와 수신기의 역할을 하는 시료 근처에 배치된다.이것은 생성된 신호가 변환기를 향해 다시 반사될 수 있는 반사 인터페이스를 필요로 하며, 변환기는 반사된 신호를 기록하는 수신기 역할을 한다.일부 측정 시스템은 초음파 테스트를 참조하십시오.
종단 및 편극 전단파
위에서 설명한 바와 같이, 솔리드의 특정 전파 방향 에 대해 입자 운동의 세 가지 정형 편광( {\ {n세트가 존재한다.탐상 중인 샘플에 직접 변환기를 고정할 수 있는 측정 설정의 경우 원하는 양극화(예: 필요한 진동 모가 있는 압전 변환기)를 서로 다른 유형의 변환기를 적용하여 이러한 세 가지 편광(종방향 및 직교 횡파 2개)을 생성할 수 있다.de). 따라서 변환기 유형의 선택에 따라 시간 의존적 또는 주파수 의존적 측정 설정을 통해 세 가지 극화 모두로 파장의 음속을 측정할 수 있다.단, 변환기를 시험 표본에 고정할 수 없는 경우, 변환기에서 시료로 음향 에너지를 전달하기 위해 연결 매체가 필요하다.물이나 젤은 종종 이 연결 매체로 사용된다.종방향 음속 측정에 있어 이 정도면 충분하지만 유체는 전단파를 전달하지 않으므로 시험 표본에서 전단파의 속도를 생성하고 측정할 수 있으려면 입사 종파가 모드 변환을 통해 전단파를 생성하기 위해 유체/고체 표면에서 비스듬히 상호작용해야 한다.그런 다음 그러한 전단파는 유체를 통해 다시 기록 변환기로 전파되는 고체/유체 표면에서 종파로 다시 변환되어 결합 매체를 통해서도 전단파 속도를 측정할 수 있다.
적용들
엔지니어링 재료 – 응력 추정
업계가 정비·보수 비용 절감을 위해 노력함에 따라, 주요 인프라의 활용과 상태를 측정하기 위한 수단으로서, 생산관리에서뿐만 아니라, 핵심 인프라의 비파괴시험에 대한 평가도 높아지고 있다.재료의 응력을 측정하는 몇 가지 측정 기법이 있다.그러나 광학 측정, 자기 측정, X선 회절, 중성자 회절 등을 이용한 기법은 모두 표면의 측정이나 표면 응력이나 변종 근처로 한정된다.음향파는 물질을 통해 쉽게 전파되며 따라서 구조물의 내부를 탐사할 수 있는 수단을 제공하는데, 여기서 응력과 변형 수준은 전체적인 구조 건전성을 위해 중요하다.이러한 비선형 탄성 재료(알루미늄 및 강철과 같은 일반적인 건설 재료를 포함)의 음속은 응력 의존성을 가지므로, 음향 효과의 적용은 측정을 위해 다양한 음향 프로브(예: 초음파 시험)를 활용하는 하중 재료 내부의 응력 상태를 측정하는 것일 수 있다.음속 변화
미세 및 다공성 물질 – 지구물리학
지진학은 지구를 통한 탄성파의 전파를 연구하며, 지진 연구와 지구 내부의 지도 작성에 사용된다.지구의 내부는 다른 압력에 의해 영향을 받고, 따라서 음향 신호는 다른 응력 상태에서 매체를 통과할 수 있다.따라서 음향탄성 이론은 지구물리학적 특성을 추정하기 위해 비선형 파동 행동을 사용할 수 있는 경우에 실용적으로 관심을 가질 수 있다.[8]
연조직 – 의료용 초음파
다른 애플리케이션은 관련 탄성 조직 유형(예: )의 스트레스 또는 압력 수준을 측정하는 의료 초음파 및 탄성 측정에 있을 수 있으며 [19][20][21]비침습성 진단을 강화할 수 있다.
참고 항목
참조
- ^ a b c d e f Ogden, R. W., 비선형 탄성 변형, 도버 출판사, 마이놀라, 뉴욕 (1984)
- ^ Brillouin, Léon (1925). "Les tensions de radiation ; leur interprétation en mécanique classique et en relativité". Journal de Physique et le Radium. 6 (11): 337–353. doi:10.1051/jphysrad:01925006011033700. ISSN 0368-3842.
- ^ Tang, Sam (1967). "Wave propagation in initially-stressed elastic solids". Acta Mechanica. 4 (1): 92–106. doi:10.1007/BF01291091. ISSN 0001-5970. S2CID 121910597.
- ^ a b c Murnaghan, F. D. (1937). "Finite Deformations of an Elastic Solid". American Journal of Mathematics. 59 (2): 235–260. doi:10.2307/2371405. ISSN 0002-9327. JSTOR 2371405.
- ^ Hughes, D. S.; Kelly, J. L. (1953). "Second-Order Elastic Deformation of Solids". Physical Review. 92 (5): 1145–1149. Bibcode:1953PhRv...92.1145H. doi:10.1103/PhysRev.92.1145. ISSN 0031-899X.
- ^ "Anisotropy and Isotropy". Archived from the original on 2012-05-31. Retrieved 2013-12-07.
- ^ a b c Norris, A. N. (1997). "Finite-Amplitude Waves in Solids". In Hamilton, Mark F.; Blackstock, David T. (eds.). Nonlinear Acoustics. Acoustical Society of America. ISBN 978-0123218605.
- ^ a b c d e f Norris, A. N. (2007). "Small-on-Large Theory with Applications to Granular Materials and Fluid/Solid Systems" (PDF). In M. Destrade; G. Saccomandi (eds.). Waves in Nonlinear Pre-Stressed Materials. CISM Courses and Lectures. Vol. 495. Springer, Vienna. doi:10.1007/978-3-211-73572-5. ISBN 978-3-211-73572-5.
- ^ a b 엘데빅, S, "음향공명을 이용한 철강 내 비선형 음향탄성 효과 측정", 베르겐대 박사논문(준비 중)
- ^ a b c d e Ogden, R. W. (2007). "Incremental Statics and Dynamics of Pre-Stressed Elastic Materials" (PDF). In M. Destrade; G. Saccomandi (eds.). Waves in Nonlinear Pre-Stressed Materials. CISM Courses and Lectures. Vol. 495. Springer, Vienna. doi:10.1007/978-3-211-73572-5. ISBN 978-3-211-73572-5.
- ^ a b Landau, L. D.; Lifshitz, E. M. (1970). Theory of Elasticity (second ed.). Pergamon Press. ISBN 9780080064659.
- ^ Toupin, R. A.; Bernstein, B. (1961). "Sound Waves in Deformed Perfectly Elastic Materials. Acoustoelastic Effect". The Journal of the Acoustical Society of America. 33 (2): 216–225. Bibcode:1961ASAJ...33..216T. doi:10.1121/1.1908623. ISSN 0001-4966.
- ^ Bland, D. R, 비선형 동적 탄성, Blaisdell Waltham, (1969)
- ^ 수구비, E.S., 에린, A. C., 엘라스타이나믹스, 학술지 뉴욕, (1974)
- ^ a b c d e Smith, R. T.; Stern, R.; Stephens, R. W. B. (1966). "Third‐Order Elastic Moduli of Polycrystalline Metals from Ultrasonic Velocity Measurements". The Journal of the Acoustical Society of America. 40 (5): 1002–1008. Bibcode:1966ASAJ...40.1002S. doi:10.1121/1.1910179. ISSN 0001-4966.
- ^ Crecraft, D.I. (1967). "The measurement of applied and residual stresses in metals using ultrasonic waves". Journal of Sound and Vibration. 5 (1): 173–192. Bibcode:1967JSV.....5..173C. doi:10.1016/0022-460X(67)90186-1. ISSN 0022-460X.
- ^ a b Egle, D. M.; Bray, D. E. (1976). "Measurement of acoustoelastic and third‐order elastic constants of rail steel". The Journal of the Acoustical Society of America. 59 (S1): S32. Bibcode:1976ASAJ...59...32E. doi:10.1121/1.2002636. ISSN 0001-4966.
- ^ Abiza, Z.; Destrade, M.; Ogden, R.W. (2012). "Large acoustoelastic effect". Wave Motion. 49 (2): 364–374. arXiv:1302.4555. doi:10.1016/j.wavemoti.2011.12.002. ISSN 0165-2125. S2CID 119244072.
- ^ Gennisson, J.-L.; Rénier, M.; Catheline, S.; Barrière, C.; Bercoff, J.; Tanter, M.; Fink, M. (2007). "Acoustoelasticity in soft solids: Assessment of the nonlinear shear modulus with the acoustic radiation force". The Journal of the Acoustical Society of America. 122 (6): 3211–3219. Bibcode:2007ASAJ..122.3211G. doi:10.1121/1.2793605. ISSN 0001-4966. PMID 18247733.
- ^ Jun Wu; Wei He; Wei-min Chen; Lian Zhu (2013). "Research on simulation and experiment of noninvasive intracranial pressure monitoring based on acoustoelasticity effects". Medical Devices: Evidence and Research. 6: 123–131. doi:10.2147/MDER.S47725. PMC 3758219. PMID 24009433.
- ^ Duenwald, Sarah; Kobayashi, Hirohito; Frisch, Kayt; Lakes, Roderic; Vanderby, Ray (2011). "Ultrasound echo is related to stress and strain in tendon". Journal of Biomechanics. 44 (3): 424–429. doi:10.1016/j.jbiomech.2010.09.033. ISSN 0021-9290. PMC 3022962. PMID 21030024.






 ) 변형
) 변형 







 함께 두 번째 순서
함께 두 번째 순서 





 (를) 조정하기 위한 참조
(를) 조정하기 위한 참조 







 스트레스의 척도인 반면,
스트레스의 척도인 반면,


























 위상파 속도,
위상파 속도, 


![{\displaystyle [{\boldsymbol {Q}}({\boldsymbol {N}})]_{ik}=B_{ijkl}N_{j}N_{l}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7202b752ff3a967c43db99681b01889909c97526)
 대해 평면파에 해당하는 가능한 파형의 속도 및 양극화를 결정한다.파동 속도는
대해 평면파에 해당하는 가능한 파형의 속도 및 양극화를 결정한다.파동 속도는 
 (가)
(가)  (가)
(가) 









 상수다.탄성 moduli 더 잘 라메 매개 변수로 알려진 그 상수 λ{\lambda\displaystyle}과μ{\displaystyle \mu}두번째 주문, 세번째 주문 탄성 moduli by,[11]지만에 내가, m해당하는 대체 있{\displays 소개되는 동안 A, B,{\displaystyle A, B}, C{C\displaystyle}.tyl
상수다.탄성 moduli 더 잘 라메 매개 변수로 알려진 그 상수 λ{\lambda\displaystyle}과μ{\displaystyle \mu}두번째 주문, 세번째 주문 탄성 moduli by,[11]지만에 내가, m해당하는 대체 있{\displays 소개되는 동안 A, B,{\displaystyle A, B}, C{C\displaystyle}.tyl




































































![X_i \in [0,L_i],\, i=1,2,3](https://wikimedia.org/api/rest_v1/media/math/render/svg/4ba9a026fa6b2db772d94fc87417ffef4babdf98)
















![e_2,e_3 \in (-1,0]](https://wikimedia.org/api/rest_v1/media/math/render/svg/994c18ffc1d88f4fe9021727e146f34d6c14e6c1)






![\boldsymbol{N}=[0,0,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/faac30d520fd4d25969024cfbfacc0523f112193)
![{\displaystyle \{{\boldsymbol {m}}\}={\begin{cases}\mathbf {m} _{1}=\mathbf {\hat {x}} _{1}=[1,0,0]&\|\,{\text{to applied tension}}\\\mathbf {m} _{2}=\mathbf {\hat {x}} _{2}=[0,1,0]&\perp {\text{to applied tension}}\\\mathbf {m} _{3}=\mathbf {\hat {x}} _{3}=[0,0,1]&\|\,{\textrm {to}}\,\mathbf {N} \end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ba2a3e07252fdcd8777d09551890b1b0eb99204)













 신호가 이동하는 거리이고
신호가 이동하는 거리이고 



