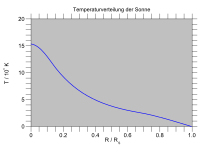
별의 구조

태양의 단면

별의 구조 모형은 별의 내부 구조를 자세히 설명하고 별의 광도, 색상, 그리고 미래의 진화에 대해 예측합니다.별의 다른 등급과 나이는 원소 구성과 에너지 전달 메커니즘을 반영하는 다른 내부 구조를 가지고 있다.

에너지 수송

고질량, 중간질량 및 저질량 별의 서로 다른 이동 메커니즘

별의 다른 층은 대류와 복사 전달 등 다양한 방식으로 열을 외부로 전달하지만, 백색왜성에서 열 전도는 중요합니다.

대류는 온도 경사가 충분히 급할 때 에너지 수송의 지배적인 형태이며, 단열 과정을 통해 별 안에 있는 가스 덩어리가 약간 상승하더라도 계속 상승할 것입니다.이 경우 상승 소포가 부력이 되어 주변 가스보다 따뜻하면 계속 상승하고 상승 소포가 주변 가스보다 시원하면 원래 ^[1]높이로 떨어집니다.낮은 온도 구배와 방사선을 통한 에너지 전송이 가능할 만큼 낮은 불투명도를 가진 영역에서는 방사선이 에너지 전송의 지배적인 모드이다.

주계열성의 내부 구조는 별의 질량에 따라 달라집니다.

태양을 포함한 질량이 0.3~M_☉1.5 태양 질량의 별에서 수소-헬륨 융합은 주로 양성자-양성자 사슬을 통해 일어나며, 이는 급격한 온도 구배를 형성하지 않는다.따라서 태양질량별의 안쪽 부분은 방사선이 지배적이다.태양질량별의 바깥쪽 부분은 수소가 중성이고 따라서 자외선 광자에 불투명하기 때문에 대류가 지배적이다.따라서 태양질량별은 별 바깥쪽에 대류성 외피가 있는 복사핵을 가지고 있다.

질량이 큰 별(약 1.5 이상)에서는 중심 온도가 약 1.8×10K⁷ 이상이기 때문에 주로 CNO 사이클을 통해 수소-헬륨 융합이 일어난다.CNO 사이클에서 에너지 생성 속도는 15번째 전력에 대한 온도와 같이 조정되는 반면, 양성자-양성자 ^[2]사슬의 4번째 전력에 대한 온도로 조정됩니다.CNO 주기의 강한 온도 민감성 때문에, 별의 내부 부분의 온도 구배는 중심부가 대류할 정도로 가파르다.별의 바깥쪽은 온도 경사가 더 낮지만 수소가 거의 완전히 이온화될 정도로 온도가 높기 때문에 별은 자외선에 투명하게 유지됩니다.따라서, 질량이 큰 별들은 복사 외피를 가지고 있다.

가장 낮은 질량의 주계열성에는 방사선 구역이 없으며, 별 전체에 걸친 주요 에너지 전달 메커니즘은 ^[3]대류이다.

항성 구조 방정식

태양 온도 프로파일

태양에서 주어진 반지름 내부의 질량

태양에서의 밀도 프로파일

태양에서의 압력 프로필

가장 일반적으로 사용되는 항성 구조 모형은 구대칭 준정적 모형으로, 항성이 정상 상태에 있고 구대칭 상태라고 가정합니다.여기에는 4개의 기본적인 1차 미분 방정식이 포함되어 있습니다. 2개는 물질과 압력이 반지름에 따라 어떻게 변화하는지를 나타내고, 2개는 온도와 밝기가 ^[4]반지름에 따라 어떻게 변화하는지를 나타냅니다.

별의 구조 방정식(구면 대칭을 가정한)을 형성할 때 물질 밀도 $\rho (r)$ ( $\rho (r)$ ) \ $displaystyle \rho ( r$ ) $\rho (r)$ 、 $T(r)$ T ( $T(r)$ ) \ $displaystyle$ T ( $T(r)$ $r$ ) $T(r)$ 、 총 압력 ( 물질 + 복사) $P(r)$ ( $P(r)$ ) \ $displaystyle$ $P(r)$ l $( r$ ) $l(r)$ 、。단위 질량당 생성 속도 $\epsilon (r)$ ( $\epsilon (r)$ ) \ $displaystyle$ $\epsilon (r)$ \ ${\mbox{d}}r$ $ipsilon ( r$ ) 별 중심에서 $\epsilon (r)$ $r$ \ $displaystyle$ r ${\mbox{d}}r$ $r$ \ $mbox$ { $d} r$ 。이 별은 국소 열역학 평형(LTE)에 있는 것으로 추정되기 때문에 물질과 광자의 온도는 동일합니다.주어진 셸 아래의 온도가 항상 위의 온도보다 더 높기 때문에 LTE가 엄격하게 유지되지는 않지만, 이러한 근사치는 일반적으로 우수합니다. 왜냐하면 광자 평균 자유 $\lambda$ 인 $"\displaystyle \lambda$ }"는 온도가 상당히 변화하는 길이보다 훨씬 작기 때문입니다. 즉, 예를 들어, " $\lambda \ll T/|\nabla T|$ 입니다. $\lambda \ll T/|\nabla T|$ § $T$ \ $displaystyle$ \ $lambda$ \ $ll$ T / \ $nabla$ T $\lambda \ll T/|\nabla T|$ } $\lambda \ll T/|\nabla T|$ 。

첫 번째는 정역학적 균형에 대한 진술입니다: 별 내부의 압력 구배에 의한 외부 힘은 중력에 의한 내부 힘에 의해 정확하게 균형을 잡습니다.이것은 때때로 항성 평형이라고 불린다.

{{\mbox{d}}P \over {\mbox{d}}r}=-{Gm\rho  \over r^{2}}

P

{{\mbox{d}}P \over {\mbox{d}}r}=-{Gm\rho  \over r^{2}}

r

=

-

{{\mbox{d}}P \over {\mbox{d}}r}=-{Gm\rho  \over r^{2}}

{{\mbox{d}}P \over {\mbox{d}}r}=-{Gm\rho  \over r^{2}}

†

{{\mbox{d}}P \over {\mbox{d}}r}=-{Gm\rho  \over r^{2}}

{{\mbox{d}

P \

over

{

mbox{d}}r}=- {Gm\rho

\

over

r

^{2

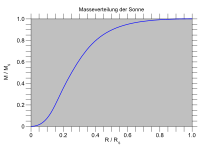
$m(r)$ 서 m $m(r)$ $)$ { $displaystyle$ m $(r)}$ 은 $m(r)$ r{ $displaystyle$ r $}$ 에서 $r$ 셸 내부의 누적 질량이고 G는 중력 상수입니다.누적 질량은 질량 연속성 방정식에 따라 반지름에 따라 증가합니다.

{{\mbox{d}}m\over{mbox{d}r}=4\pi r^{2}\rho.

별의 중심( $r$ $r=0$ 0 { $r=0$ 스타일 r $=$ $0$ )에서 별의 반지름( $r=R$ $r=R$ {\ $디스플레이$ 스타일 $r=$ R $r=R$ 까지 질량 연속성 방정식을 통합하면 별의 총 질량이 산출됩니다.

구형 쉘에서 나오는 에너지를 고려하면 다음과 같은 에너지 방정식이 생성됩니다.

{{\mbox{d}}l \over {\mbox{d}}r}=4\pi r^{2}\rho (\epsilon -\epsilon _{\nu })

{{\mbox{d}}l \over {\mbox{d}}r}=4\pi r^{2}\rho (\epsilon -\epsilon _{\nu })

{{\mbox{d}}l \over {\mbox{d}}r}=4\pi r^{2}\rho (\epsilon -\epsilon _{\nu })

r

{{\mbox{d}}l \over {\mbox{d}}r}=4\pi r^{2}\rho (\epsilon -\epsilon _{\nu })

{{\mbox{d}}l \over {\mbox{d}}r}=4\pi r^{2}\rho (\epsilon -\epsilon _{\nu })

{{\mbox{d}}l \over {\mbox{d}}r}=4\pi r^{2}\rho (\epsilon -\epsilon _{\nu })

{{\mbox{d}}l \over {\mbox{d}}r}=4\pi r^{2}\rho (\epsilon -\epsilon _{\nu })

2

{{\mbox{d}}l \over {\mbox{d}}r}=4\pi r^{2}\rho (\epsilon -\epsilon _{\nu })

(

{{\mbox{d}}l \over {\mbox{d}}r}=4\pi r^{2}\rho (\epsilon -\epsilon _{\nu })

ϵ -

{{\mbox{d}}l \over {\mbox{d}}r}=4\pi r^{2}\rho (\epsilon -\epsilon _{\nu })

） {

displaystyle

{ \

mbox

{

d } l

\

over

{ \

mbox

{ d } r

{{\mbox{d}}l \over {\mbox{d}}r}=4\pi r^{2}\rho (\epsilon -\epsilon _{\nu })

=

{{\mbox{d}}l \over {\mbox{d}}r}=4\pi r^{2}\rho (\epsilon -\epsilon _{\nu })

4 \

pi r^

{2

}

\

rho ( \

explilon

- \

explon

_ { \

nu }

)

{{\mbox{d}}l \over {\mbox{d}}r}=4\pi r^{2}\rho (\epsilon -\epsilon _{\nu })

,

여기서 $(\$ _ ${\nu })$ 는 $\epsilon _{\nu }$ 단위 질량당 중성미자의 형태로 생성되는 광도이다.핵반응이 일어나는 별의 중심부 밖에서는 에너지가 생성되지 않기 때문에 광도는 일정합니다.

에너지 수송 방정식은 에너지 수송 방식에 따라 다른 형태를 취합니다.전도성 에너지 수송(백색 왜성에 적합)의 경우 에너지 방정식은 다음과 같습니다.

{{\mbox{d}}T \over {mbox{d}r}=-{1 \over k}{l \over 4\pi r^{2}}}

여기서 k는 열전도율입니다.

태양질량 주계열성의 내부 부분과 질량이 큰 주계열성의 외부 외피층에 적합한 복사 에너지 수송의 경우,

{{\mbox{d}}T \over {mbox{d}r}=-{3\kappa \rho l \over 64\pi r^{2}\pi r^{3}},

$\kappa$ 서 ${\(\displaystyle$ \ $kappa)$ 는 $\kappa$ 물질의 불투명도이고 {\(\ $displaystyle \sigma)$ 는 $\sigma$ 스테판-볼츠만 상수이며 볼츠만 상수는 1로 설정됩니다.

대류 에너지 수송의 경우 알려진 엄격한 수학 공식은 없으며 기체 내 난류를 수반한다.대류 에너지 수송은 일반적으로 혼합 길이 이론을 사용하여 모델링됩니다.이것은 별에 있는 가스를 주변의 온도, 밀도 및 압력을 대략 유지하면서도 혼합 ^[5]길이라고 불리는 특징적인 길이로 별을 통해 이동하는 개별적인 원소를 포함하는 것으로 간주합니다.단원자 이상 기체의 경우, 대류가 단열일 때, 대류 기포가 주변과 열을 교환하지 않는다는 것을 의미하며, 혼합 길이 이론이 산출됩니다.

{{\mbox{d}}T \over {mbox{d}r}=\left(1-{1 \over \mbox }\오른쪽){T \over P}{\mbox{d}P \over {mbox{d}r}}

여기서 $\gamma =c_{p}/c_{v}$ $\gamma =c_{p}/c_{v}$ / $\gamma =c_{p}/c_{v}$ $\gamma =c_{p}/c_{v}$ { $displaystyle$ \ $displaystyle = c_{p}/c_{v}}$ 는 $\gamma =c_{p}/c_{v}$ 기체 내 비열 비율이다.(완전 이온화된 이상 기체의 경우 $\gamma =5/3$ $=$ $\gamma =5/3$ /3(\ $displaystyle$ \ $displaystyle$ = 5 $/3$ ). $\gamma =5/3$ 대류가 단열하지 않을 때 이 온도 방정식은 주어지지 않는다.예를 들어, 태양에서는 중심 부근의 대류 구역의 밑부분의 대류는 단열이지만 표면 부근의 대류는 그렇지 않습니다.혼합 길이 이론은 두 개의 자유 매개변수를 포함하며, 이는 모형을 관측치에 적합하게 만들기 위해 설정되어야 하므로, 엄격한 수학 ^[6]공식이라기보다는 현상론 이론입니다.

또한 압력, 불투명도 및 에너지 생성 속도를 온도, 밀도, 화학 조성 등 재료에 적합한 다른 국소 변수에 관련짓는 상태 방정식이 필요하다.압력에 대한 관련 상태 방정식에는 완벽한 가스 법칙, 복사 압력, 퇴화 전자에 의한 압력 등이 포함되어야 할 수 있습니다.불투명도는 하나의 공식으로 정확하게 표현할 수 없습니다.특정 밀도 및 온도에서 다양한 구성에 대해 계산되어 표 ^[7]형식으로 표시됩니다.별의 구조 코드(모델의 변수를 계산하는 컴퓨터 프로그램을 의미)는 밀도-온도 그리드에 보간하여 필요한 불투명도를 얻거나 표 값을 기반으로 한 적합 함수를 사용합니다.상태 압력 방정식의 정확한 계산에도 유사한 상황이 발생합니다.마지막으로 핵에너지 생성률은 핵물리학 실험에서 계산되며, 반응 네트워크를 사용하여 각 개별 반응 단계에 대한 반응 속도와 기체 ^[6]^[8]내 각 동위원소에 대한 평형 농도를 계산한다.

일련의 경계 조건과 결합된 이 방정식의 해는 별의 행동을 완전히 묘사합니다.일반적인 경계 조건은 별의 표면( $r=R$ $r=R$ { $displaystyle$ r $=R$ 및 중심( $r=0$ $r=0$ { $displaystyle$ r $=0$ 에서 관측 가능한 매개 변수의 값을 적절하게 $P(R)=0$ 합니다. 즉 $P(R)=0$ P ( $m(0)=0$ $P(R)=0$ $P(R)=0$ { $displaystyle$ P $(R$ ) $m(0)=0$ $0$ 즉 별의 표면에서의 압력은 0 $display$ 0 $)$ 입니다. $m(R)=M$ 밀도가 유한한 경우 별의 중심 내부에 질량이 없다. m $m(R)=M$ ( $m(R)=M$ ) $=$ $m(R)=M$ ${\displaystyle$ m $(R$ )= $M$ $T(R)=T_{eff}$ 의 총 질량은 별의 질량이다. 그리고 T ( $=$ $T(R)=T_{eff}$ $T(R)=T_{eff}$ { $displaystyle$ T $(R$ )= $T_{eff$ 표면 온도는 별의 유효 온도입니다.

오늘날 별의 진화 모델은 색상 크기 다이어그램의 주요 특징을 설명하지만 운송 현상에 대한 제한된 지식과 관련된 불확실성을 제거하기 위해 중요한 개선이 이루어져야 한다.가장 어려운 과제는 ^{[citation needed]}난류의 수치적 처리이다.일부 연구팀은 3D 계산에서 난류의 단순화된 모델링을 개발하고 있습니다.

급속한 진화

위의 단순화된 모델은 구성 변화가 충분히 빠른 상황에서 수정 없이 적절하지 않습니다.정역학적 평형의 방정식은 별의 반지름이 매우 빠르게 변화하는 경우(예: 별이 방사상으로 ^[9]맥동하는 경우) 반경 가속 항을 추가하여 수정해야 할 수 있습니다.또한 핵연소가 안정적이지 않거나 별의 핵이 급격히 붕괴하고 있다면 에너지 ^[10]방정식에 엔트로피 항을 추가해야 합니다.

「」를 참조해 주세요.

레퍼런스

^ Hansen, Kawaler & Trimble (2004, Tbl.1)
^ 이 논의는 예를 들어 Zeilik & Gregory(1998년, §16-1–16-2)와 Hansen, Kawaler & Trimble(2004년, §7.1)의 논의에 따른다.
^ Hansen, Kawaler & Trimble (2004년, 5.1엔)
^ ^a ^b Ostlie, Dale A. 및 Carrol, Bradley W., Addison-Wesley, 현대별 천체물리학 소개 (2007)
^ Iglesias, C. A.; Rogers, F. J. (June 1996), "Updated Opal Opacities", Astrophysical Journal, 464: 943–+, Bibcode:1996ApJ...464..943I, doi:10.1086/177381.
^ Rauscher, T.; Heger, A.; Hoffman, R. D.; Woosley, S. E. (September 2002), "Nucleosynthesis in Massive Stars with Improved Nuclear and Stellar Physics", The Astrophysical Journal, 576 (1): 323–348, arXiv:astro-ph/0112478, Bibcode:2002ApJ...576..323R, doi:10.1086/341728.
^ Moya, A.; Garrido, R. (August 2008), "Granada oscillation code (GraCo)", Astrophysics and Space Science, 316 (1–4): 129–133, arXiv:0711.2590, Bibcode:2008Ap&SS.316..129M, doi:10.1007/s10509-007-9694-2, S2CID 16150778.
^ Mueller, E. (July 1986), "Nuclear-reaction networks and stellar evolution codes – The coupling of composition changes and energy release in explosive nuclear burning", Astronomy and Astrophysics, 162 (1–2): 103–108, Bibcode:1986A&A...162..103M.

원천

Kippenhahn, R.; Weigert, A. (1990), Stellar Structure and Evolution, Springer-Verlag
Hansen, Carl J.; Kawaler, Steven D.; Trimble, Virginia (2004), Stellar Interiors (2nd ed.), Springer, ISBN 0-387-20089-4
Kennedy, Dallas C.; Bludman, Sidney A. (1997), "Variational Principles for Stellar Structure", Astrophysical Journal, 484 (1): 329–340, arXiv:astro-ph/9610099, Bibcode:1997ApJ...484..329K, doi:10.1086/304333, S2CID 16835178
Weiss, Achim; Hillebrandt, Wolfgang; Thomas, Hans-Christoph; Ritter, H. (2004), Cox and Giuli's Principles of Stellar Structure, Cambridge Scientific Publishers, Bibcode:2004cgps.book.....W
Zeilik, Michael A.; Gregory, Stephan A. (1998), Introductory Astronomy & Astrophysics (4th ed.), Saunders College Publishing, ISBN 0-03-006228-4

외부 링크

2009년 11월 불투명도 코드 취득
노란색 CESAM 코드, 별의 진화 및 구조 Fortran 소스 코드
Eggleton의 Stellar Evolution Code에서 파생된 FORTRAN 90 소프트웨어인 Evolution ZAMS Stars는 여기에서 웹 기반 인터페이스를 찾을 수 있습니다[1].
제네바 항성 진화 모델 그리드(일부 회전 유도 혼합 포함)
별의 진화 궤적에 대한 BaaSTI 데이터베이스

[1] Hansen, Kawaler & Trimble (2004, © 5.1.1)

[2] Hansen, Kawaler & Trimble (2004, Tbl.1)

[3] Hansen, Kawaler & Trimble (2004, © 2.2.1)

[4] 이 논의는 예를 들어 Zeilik & Gregory(1998년, §16-1–16-2)와 Hansen, Kawaler & Trimble(2004년, §7.1)의 논의에 따른다.

[5] Hansen, Kawaler & Trimble (2004년, 5.1엔)

[Ostlie-6] Ostlie, Dale A. 및 Carrol, Bradley W., Addison-Wesley, 현대별 천체물리학 소개 (2007)

[Rogers1996-7] Iglesias, C. A.; Rogers, F. J. (June 1996), "Updated Opal Opacities", Astrophysical Journal, 464: 943–+, Bibcode:1996ApJ...464..943I, doi:10.1086/177381.

[Heger2002-8] Rauscher, T.; Heger, A.; Hoffman, R. D.; Woosley, S. E. (September 2002), "Nucleosynthesis in Massive Stars with Improved Nuclear and Stellar Physics", The Astrophysical Journal, 576 (1): 323–348, arXiv:astro-ph/0112478, Bibcode:2002ApJ...576..323R, doi:10.1086/341728.

[9] Moya, A.; Garrido, R. (August 2008), "Granada oscillation code (GraCo)", Astrophysics and Space Science, 316 (1–4): 129–133, arXiv:0711.2590, Bibcode:2008Ap&SS.316..129M, doi:10.1007/s10509-007-9694-2, S2CID 16150778.

[10] Mueller, E. (July 1986), "Nuclear-reaction networks and stellar evolution codes – The coupling of composition changes and energy release in explosive nuclear burning", Astronomy and Astrophysics, 162 (1–2): 103–108, Bibcode:1986A&A...162..103M.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

Search

별의 구조

네임스페이스

더

목차

에너지 수송

항성 구조 방정식

급속한 진화

「」를 참조해 주세요.

레퍼런스

원천

외부 링크

Search

별의 구조

에너지 수송

항성 구조 방정식

급속한 진화

「 」를 참조해 주세요.

레퍼런스

원천

외부 링크

「」를 참조해 주세요.