축척 높이

대기, 지구 및 행성 과학에서 축척 높이(일반적으로 대문자 H로 표시됨)는 물리적 양이 e의 계수(자연 로그의 기저값, 약 2.718)만큼 감소하는 거리(수직 또는 방사형)입니다.

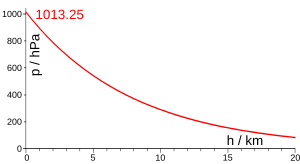
단순 대기압 모델에 사용되는 스케일 높이

행성 대기의 경우, 스케일 높이는 대기압이 e의 계수만큼 감소하는 고도의 증가이다.스케일 높이는 특정 온도에 대해 일정하게 유지됩니다.그것은 다음과^[1][2] 같이 계산할 수 있다.

${\displaystyle H=black {kT}{mg}}$

또는 동등하게

${\displaystyle H=black {RT}{Mg}}}$

여기서:

• k = 볼츠만 상수 = 1.38 x⁻²³ 10 J·K⁻¹
• R = 가스 상수
• T = 평균 대기 온도(켈빈 단위) = 지구의 경우 250^[3] K
• m = 분자의 평균 질량(16 kg)
• M = 대기 입자 1몰의 평균 질량 = 지구의 경우 0.029 kg/mol
• g = 현재 위치의 중력에 의한 가속도(m/s²)

특정 고도에서의 압력(단위 면적당 힘)은 대기 중량의 결과이다.z의 높이에서 대기의 밀도 θ와 압력 P가 있는 경우, 극소 높이 dz를 위쪽으로 이동하면 대기층 두께 dz의 무게와 동일한 양의 dP만큼 압력이 감소합니다.

다음과 같이 됩니다.

$(\displaystyle\frac {dP}{dz}}=-g\rho }$

여기서 g는 중력에 의한 가속도입니다.작은 dz의 경우 g가 일정하다고 가정할 수 있습니다. 마이너스 부호는 높이가 증가함에 따라 압력이 감소함을 나타냅니다.따라서, 온도 T에서 평균 분자량 M의 이상적인 기체에 대한 상태 방정식을 사용하여, 밀도는 다음과 같이 표현될 수 있다.

${\displaystyle\rho=mp}{RT}}$

이 방정식을 조합하면

$\displaystyle\frac{dP}{P}}=param frac {-dz}{\frac {kT}{mg}}}}$

위에 제시된 H에 대한 방정식과 통합하면 다음과 같은 결과를 얻을 수 있다:

${\displaystyle {frac {dP}}=-{\frac {dz}{H}}}$

온도가 변하지 않는 한 변하지 않습니다.위의 내용을 통합하고 P가 높이 z = 0(해면 압력)이라고 가정하면₀ 높이 z에서의 압력은 다음과 같이 쓸 수 있습니다.

${\displaystyle P=P_{0}\exp \leftfac {\frac {z}{H}}\right)}$

이는 ^[4]높이가 높아짐에 따라 압력이 기하급수적으로 감소하는 것으로 해석됩니다.

지구 대기에서 해수면₀ P의 압력은 평균 1.01⁵×10Pa이며 건조한 공기의 평균 분자 질량은 28.964u이므로 m = 28.964×1.18×10⁻²⁷⁻²⁶ = 4.808×10kg이다.따라서 온도의 함수로서 지구 대기의 스케일 높이는 H/T = k/mg = (1.38/(4.808×9.81)×10³ = 29.26 m/K이다.이는 대표적인 대기 온도에 대해 다음과 같은 스케일 높이를 산출합니다.

T = 290 K, H = 8500 m

T = 273 K, H = 8000 m

T = 260 K, H = 7610 m

T = 210 K, H = 6000 m

이 인물들은 공기의 밀도 해수면에서 1200g/m3에서 0.53으로 떨어지는 것)70킬로미터 지점 .125 g/m3, 9600이다의 한 요인=약 80km70(9600이다)의 평균 규모 높이를 나타내는 값, 또 그 위 표시된 평균 기온과 증상을 보인다는 지구의 대기 NRLMSISE-00에 사울의 온도와 밀도가 비교되어야 한다. 뛰었다260K에 가까운 ge.

주의:

• 밀도는 이상적인 가스 법칙에 의해 압력과 관련이 있습니다.따라서 해수면 값에서₀ 약 1.2kgm의⁻³ 높이에 따라 밀도도 기하급수적으로 감소한다.
• 100km가 넘는 높이에서는 대기가 더 이상 잘 섞이지 않을 수 있다.그리고 각 화학종들은 그들만의 비늘 높이를 가지고 있다.
• 여기서 온도와 중력 가속도는 일정하다고 가정했지만 둘 다 먼 거리에 따라 달라질 수 있다.

행성의 예

선택된 태양계 천체에 대한 대략적인 대기 스케일 높이는 다음과 같다.

• 금성: 15.9km^[5]
• 지구: 8.5km^[6]
• 화성: 11.1km^[7]
• 목성: 27km^[8]
• 토성: 59.5km^[9]

• 타이탄: 21km^[10]

• 천왕성: 27.7km^[11]
• 해왕성: 19.1~20.3km^[12]
• 명왕성: 최대 50km^[13]

씬 디스크의 높이 확장

예를 들어 프로토스타와 같은 응축된 중심물체 주위의 가스 원반은 행성 스케일 높이와 다소 유사한 디스크 스케일 높이를 도출할 수 있다.중심 물체에 비해 질량이 작은 가스 원반부터 시작합니다.중력 성분이 디스크의 중간면을 가리키고 있는 별의 중력 z 성분과 정역학적 평형 상태에 있다고 가정합니다.

$({displaystyle {dP} {dz}}=-{\frac {GM_{*}\rho z}{(r^{2}+z^{2})^{3/2}}}})$

여기서:

• G = 중력 상수 6 6.674 x 10⁻¹¹³ m·kg⁻¹·s⁻²
• r = 별 또는 중심 응축된 물체의 중심으로부터의 거리에 대한 방사형 원통 좌표
• z = 디스크 미드플레인(또는 별의 중심)으로부터의 거리에 대한 높이/고도 원통 좌표
• M_* = 별/질량 응축 물체의 질량
• P = 디스크 내 가스의 압력
• $ρ${$displaystyle$ \rho$$} = 디스크 내 가스 질량 ${\displaystyle \mathrm{밀도}}$

$씬{\displaystyle }$ 디스크 근사에서 z$$ r \ $displaystyle$ z$\ll$r$$ 및 정수적 평형 방정식은 다음과 같다.

$({displaystyle {frac {dP} {dz}} \ about - { \ frac { GM _ { * } \ rho z } { r^ {3} } )$

가스 압력을 결정하려면 다음과 같은 이상적인 가스 법칙을 사용할 수 있습니다.

${\displaystyle P=snapsfrac {rho kT}{\bar {m}}}$

포함:

• T = 디스크의 가스 온도. 여기서 온도는 r의 함수이지만 z와는 무관합니다.
• $m =$ 가스의 평균 $분자량$

이상 기체 법칙과 정수적 평형 방정식을 사용하면 다음과 같은 결과를 얻을 수 있습니다.

${\displaystyle {d\rho }{dz}}\약 -{\frac {GM_{*}{\bar {m}}\rho z}{kTr^{3}}}}$

해답이 있다.

$({displaystyle \rho =\rho _{0}\exp \leftflac {z}{h_{D}}\right)^{2}\right)}$

${\displaystyle {여기}_{}}$서 0$({$은 별의 중심에서r 거리에 있는 디스크 미드플레인의 가스 질량 밀도이고 $({$는 다음과 같은 디스크 스케일 높이입니다.

${\displaystyle h_{D}=sqrt {frac {2kTr^{3}}}{GM_{*}{\bar {m}}}\약 0.0306{\sqrt {\frac(T/100\rm {K}}\rft(r/1\rm {au}\right)^3}{\left(M_*}/{\rm {M}}}\{\ot}\{\right}\{{\fright}\fright}\fright}{{\fright}}\fright}{\fright}\frac\fright}{\fright}{\fright}{}}\\ {rm {au}}$

M $⊙$ {\$displaystyle {M}_{\odot}$ 태양 $질량{\displaystyle \mathrm{}}$, u$\$$}$ 천문학 단위, $\$ {$amu}$ 원자 질량 단위로 $구성$됩니다.

예를 들어 온도변화 T$(\displaystyle$ T$)$를 무시하면 중심 ${\displaystyle {}^{}}$에서 반경방향으로 이동함에 따라 h D ${\displaystyle {}_{}}$ ${\displaystyle {r\mathrm{}}^{}}$3 /$$(\$displaystyle h_{D}\propto$ r$^{3/2})$가 $표시$되고 디스크의 고도가 높아집니다.

디스크 내 가스 온도 T가 z와 무관하다는 가정 때문에 h $(\$는 등온 디스크 스케일 높이라고도 합니다.

자기장의 디스크 스케일 높이

중심물체 주위의 얇은 가스 디스크 내의 자기장은 ^[14][15][16]디스크의 스케일 높이를 변경할 수 있다.예를 들어, 완전하지 않은 전도성 디스크가 폴로이드 자기장을 통해 회전하고 있는 경우(즉, 초기 자기장이 디스크의 평면에 수직인 경우), 디스크 내에서 트로이덜(즉, 디스크 평면에 평행한) 자기장이 생성되어 디스크가 꼬집혀 압축됩니다.이 경우 디스크의 가스 밀도는 다음과 같습니다.

${\displaystyle \rho (r,z)=\rho _{0}(r)\exp \leftfrac {z}{h_{D}\right)^{2}-\rho _{\cut}(r)\left [1-exp \ exp \ leftwright\frac\fracz}{h}{h}{h}{d}{h}{{{{d}}}}}{h}}{d}}}}}^{right}^{right}}}^{right}}$

여기서 컷오프 ${\displaystyle {밀도\theta \mathrm{}}_{}}$ ${\displaystyle {\mathrm{c}}_{}}$ t ${\displaystyle$ \$rho$ _${\rm {cut}}$는 다음과 같은 형태를 가진다.

$\displaystyle \rho _{\rm {cut}}(r)=(\mu _{0}\display_{D}r)^{2}\left({\frac {B_{z}^2}){\mu _{0}}\right}\frac {\frac {{{{{\displaystyp}}}}{{{{{{{{\}}}}}}}}}}}}}\flight}{\flight}{\flight}}{\fright}}}$

어디에

• ${\displaystyle {\mu \mathrm{}}_{}}$ 0$(\$은 여유 공간의 투과성입니다.
• ${\displaystyle {}_{}}$§ $(\displaystyle$ \$sigma _${D$$$})$는 디스크의 전기 전도율입니다.
• ${\displaystyle B_{}}$z(\$displaystyle B_{z})$는 z$(\displaystyle$z) 방향의$$ 폴로이드 필드의 자속 밀도입니다.
• $ω${\ （ \ $displaystyle$ \$$Omega$$ _$$ { * } ）는 중심 물체의 회전각속도입니다(폴로이드 자기장이 중심 물체와 무관할 $경우{\displaystyle {\mathrm{}}_{}}$ $ω${\ { \ $displaystyle$ \ $Omega$_ { *} can 0 으로 설정할 수 있습니다).
• $K(\displaystyle$ \$Omega _{$K$$})는 중심 물체로부터$r(\$displaystyle$$ r) $거리$에 $있는{\displaystyle }$ 디스크의 케플러 각속도입니다.

이러한 공식은 자화 디스크의 최대 ${\displaystyle {높이}_{}}$인 HB$(\$를 나타냅니다.

${\displaystyle {}_{}\sqrt{H\mathrm{}}}$ B ${\displaystyle {}_{}}$ ${\displaystyle h_{}}$ D ${\displaystyle \sqrt{\ln }}$ ${\displaystyle \sqrt{(}}$ (${\displaystyle \sqrt{}}$1 + ${\displaystyle \sqrt{{}_{}}}$ 0 / ${\displaystyle \sqrt{{\mathrm{c}}_{}}}$ c ${\displaystyle \sqrt{{\mathrm{u}}_{}}}$t$$) { $displaystyle H_{B$} =$h_{D}$ {\$sqrt {ln \left$( $1+\rho$_ {$0}$ / \$rho$ _${\rm {cut$ ,

전자 접이식 자기 스케일 $높이{\displaystyle {}_{}}$ ${\displaystyle h_{}}$ B$(\$는

${\displaystyle h_{B}=h_{D}{\sqrt(1+{\frac {1-1/e}{1/e+}\rho _{\rm {cut}}/\rho _{0}}}}}\.}$

「 」를 참조해 주세요.

• 시간 상수

레퍼런스