스핀 네트워크

루프 양자 중력에 사용되는 유형의 단순 스핀 네트워크

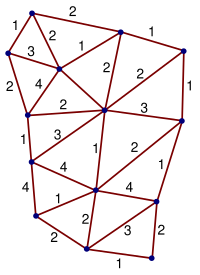
물리학에서 스핀 네트워크는 양자역학에서 입자와 장 사이의 상태와 상호작용을 나타내기 위해 사용될 수 있는 다이어그램의 일종이다.수학적인 관점에서, 도표는 행렬 그룹의 표현들 사이의 다행 함수와 함수를 나타내는 간결한 방법이다.간단한 도표는 복잡한 기능을 나타내기 위해 사용될 수 있기 때문에 도표 표기법은 종종 계산을 단순화한다.

로저 펜로즈는 1971년에 스핀 네트워크의 발명으로 인정받고 있지만,^[1] 그의 시대 이전에는 유사한 도식적 기법이 존재했다.스핀 네트워크는 카를로 로벨리, 리 스몰린, 호르헤 풀린, 로돌포 감비니 등이 양자 중력 이론에 적용했다.

스핀 네트워크는 국소 게이지 변환에 따라 불변하는 연결 공간의 특정 기능을 구성하는데도 사용될 수 있다.

정의

펜로즈의 원래 정의

스핀 네트워크는 펜로즈(1971년)^[1]에서 설명한 대로 각 선 세그먼트가 "단위"의 세계 선(초기 입자 또는 입자의 복합 시스템)을 나타내는 다이어그램의 일종이다.각 꼭지점에서 세 개의 선 세그먼트가 결합된다.꼭지점은 하나의 단위가 두 개 또는 두 개 단위로 갈라져 하나의 단위로 결합되는 사건으로 해석할 수 있다.선 세그먼트가 모두 정점에서 결합되는 도표를 폐쇄 스핀 네트워크라고 한다.시간은 다이어그램의 아래쪽에서 위쪽으로 가는 것처럼 한 방향으로 가는 것으로 볼 수 있지만, 폐쇄된 스핀 네트워크의 경우 시간의 방향은 계산과 무관하다.

각 선 세그먼트는 스핀 번호라는 정수로 라벨을 표시한다.스핀 번호 n을 가진 단위를 n-단위라고 하며 각운동량 n//2를 가지고 있는데 여기서 ħ은 축소된 플랑크 상수다.광자와 글루온과 같은 보손의 경우 n은 짝수다.전자나 쿼크와 같은 페르미온의 경우 n은 이상하다.

어떤 폐쇄된 스핀 네트워크를 주어진다면, 비 음의 정수를 계산할 수 있는데, 이를 스핀 네트워크의 표준이라고 한다.규범은 다양한 스핀 값의 확률을 계산하는 데 사용할 수 있다.표준이 0인 네트워크는 발생 확률이 0이다.규범과 확률을 계산하는 규칙은 이 글의 범위를 벗어난다.그러나 이들은 스핀 네트워크가 0이 아닌 규범을 가지려면 각 꼭지점에서 두 가지 요건을 충족해야 한다는 것을 암시한다.꼭지점이 스핀 번호 a, b, c와 세 개의 단위를 결합한다고 가정합시다.그 다음, 이러한 요구사항은 다음과 같이 명시된다.

삼각형 불평등: a는 b + c보다 작거나 같아야 하며, b는 + c보다 작거나 같아야 하며, c는 + b보다 작거나 같아야 한다.
페르미온 보존: a + b + c는 짝수여야 한다.

예를 들어 a = 3, b = 4, c = 6은 3 + 4 + 6 = 13이 홀수이므로 불가능하며, a = 3, b = 4, c = 9는 9 > 3 + 4이므로 불가능하다.단, a = 3, b = 4, c = 5는 3 + 4 + 5 = 12가 짝수이고 삼각형 불평등이 충족되기 때문에 가능하다.일부 규약에서는 합계가 + b + c여야 한다는 조건과 함께 반정수자에 의한 labelling을 사용한다.

형식 정의

좀 더 공식적으로, 스핀 네트워크는 (방향) 그래프로서, 가장자리가 컴팩트한 Lie 그룹의 수정 불가능한 표현과 연관되어 있고, 정점이 그것과 인접한 가장자리 표현들의 인터트위너와 연관되어 있다.

다지관에 담그는 스핀 네트워크를 사용하여 이 다지관의 연결 공간에 대한 기능을 정의할 수 있다.하나는 그래프의 모든 링크(폐쇄 경로)를 따라 연결의 홀로노미를 계산하고, 모든 링크에 해당하는 표현 매트릭스를 결정하고, 모든 매트릭스와 인터트위너를 함께 곱하고, 지정된 방법으로 지수를 수축한다.그 결과 기능의 주목할 만한 특징은 국소 게이지 변환에서도 불변한다는 것이다.

물리학에서의 사용법

루프 양자 중력의 맥락에서

루프 양자 중력(LQG)에서 스핀 네트워크는 3차원 초외면에 있는 중력장의 "수량 상태"를 나타낸다.가능한 모든 스핀 네트워크(또는 더 정확히 말하면, "s-knots" - 즉, 차이점형 하의 스핀 네트워크의 동등성 등급)의 집합은 셀 수 있다; 그것은 LQG Hilbert 공간의 기초를 구성한다.

루프 양자 중력의 주요 결과 중 하나는 면적의 정량화인데, 2차원 표면 σ의 면적 A의 연산자는 이산 스펙트럼을 가져야 한다.모든 스핀 네트워크는 그러한 각 운영자의 고유 상태이며, 영역 고유값은 동일하다.

A_{\Sigma }=8\pi \ell _{\text{PL}}^{2}\감마 \sum _{i}{\sqrt {j_{i}(j_{i}+1)}}}}

여기서 합계는 스핀 네트워크와 Ⅱ의 모든 교차로에 걸쳐진다.이 공식에서,

ℓ은_PL 플랑크 길이,
$\gamma$ $\gamma$ 은 $\gamma$ (는) Immirzi 매개 변수 및
j_i = 0, 1/2, 1, 3/2 는 스핀 네트워크의 링크 i와 관련된 스핀이다.따라서 2차원 영역은 스핀 네트워크와의 교차점에 "집중"된다.

이 공식에 따르면 영역 운영자의 0이 아닌 가장 낮은 고유값은 스핀 1/2 표현을 전달하는 링크에 해당한다.Imirzi 매개변수를 1의 순서로 가정할 경우, 측정 가능한 가장 작은 면적이 최대 10⁻⁶⁶ cm이다².

비정상적인 확산 모델과 같이 표면이 정점을 통과하도록 허용되면 면적 고유값의 공식은 다소 복잡해진다.또한 면적 연산자 A의 고유값은 사다리 대칭에 의해 구속된다.

유사한 정량화가 볼륨 운영자에게 적용된다.스핀 네트워크의 일부를 포함하는 3D 서브매니폴드의 볼륨은 그 안에 있는 각 노드의 기여도의 합에 의해 주어진다.스핀 네트워크의 모든 노드는 기본적인 "볼륨의 수량"이며 모든 링크는 이 볼륨을 둘러싼 "영역의 수량"이라고 생각할 수 있다.

더 일반적인 게이지 이론

컴팩트한 Lie 그룹 G와 연결 형태를 가진 일반 게이지 이론에도 유사한 구조를 만들 수 있다.이것은 사실 격자 위에 있는 정확한 이중성이다.그러나 다지관 위에선 이중성을 정확하게 만들기 위해 차이점형 불변성과 같은 가정이 필요하다(윌슨 루프를 숨기는 것은 까다롭다).이후 로버트 오클에 의해 타나카-크레인 이원성을 이용하여 양자 집단을 2차원과 3차원으로 나타내는 것이 일반화되었다.

마이클 A. Levin과 Xiao-Gang Wen은 또한 스핀 네트워크와 매우 유사한 개체인 텐서 범주를 사용하여 문자열망을 정의했다.그러나 스핀 네트워크와의 정확한 연결은 아직 명확하지 않다.줄망 응결은 응축된 물질에서 위상순으로 상태를 생성한다.

수학에서의 사용법

수학에서 스핀 네트워크는 연결 공간에 해당하는 skin 모듈이나 캐릭터 변종을 연구하는 데 이용되어 왔다.

참고 항목

참조

^ ^a ^b R. 펜로스(1971a), T. 바스틴(ed.), 양자 이론 및 비욘드(Beyond), 캠브리지 대학 출판부의 "사각형 모멘텀: 콤비네이터 스페이스타임에 대한 접근법" (이 논문은 존 C에서 온라인으로 볼 수 있다. Baez의 웹사이트) 및 R.Penrose(1971b), D. J. A.의 "부차원의 텐서 적용".웨일스(ed.), 결합 수학 및 응용 프로그램(Proc).콘프, 옥스포드, 1969), 학술지, 페이지 221–244, esp. 241 (후자 논문은 1969년에 발표되었으나 1971년에 로저 펜로즈에 따르면: I. 로빈슨, 비브립폴리스, 나폴리 1987년 명예의 권인 중력과 기하학에 관하여)에서 출판되었다.

추가 읽기

조간신문

I. B. 레빈슨 "위그너 계수의 합계 및 그 그래픽 표현"을 진행하십시오. 물리 기술 주식회사. Acad Sci. 리투아니아 SSR 2, 17-30 (1956년)
Kogut, John; Susskind, Leonard (1975). "Hamiltonian formulation of Wilson's lattice gauge theories". Physical Review D. 11 (2): 395–408. Bibcode:1975PhRvD..11..395K. doi:10.1103/PhysRevD.11.395.
Kogut, John B. (1983). "The lattice gauge theory approach to quantum chromodynamics". Reviews of Modern Physics. 55 (3): 775–836. Bibcode:1983RvMP...55..775K. doi:10.1103/RevModPhys.55.775. (유클리드 고온(강력 커플링) 섹션 참조)
Savit, Robert (1980). "Duality in field theory and statistical systems". Reviews of Modern Physics. 52 (2): 453–487. Bibcode:1980RvMP...52..453S. doi:10.1103/RevModPhys.52.453. (아벨 게이지 이론에 대한 섹션 참조)

현대 신문

Rovelli, Carlo; Smolin, Lee (1995). "Spin networks and quantum gravity". Phys. Rev. D. 52 (10): 5743–5759. arXiv:gr-qc/9505006. Bibcode:1995PhRvD..52.5743R. doi:10.1103/PhysRevD.52.5743. PMID 10019107. S2CID 16116269.
Pfeiffer, Hendryk; Oeckl, Robert (2002). "The dual of non-Abelian Lattice Gauge Theory". Nuclear Physics B - Proceedings Supplements. 106–107: 1010–1012. arXiv:hep-lat/0110034. Bibcode:2002NuPhS.106.1010P. doi:10.1016/S0920-5632(01)01913-2. S2CID 14925121.
Pfeiffer, Hendryk (2003). "Exact duality transformations for sigma models and gauge theories". Journal of Mathematical Physics. 44 (7): 2891–2938. arXiv:hep-lat/0205013. Bibcode:2003JMP....44.2891P. doi:10.1063/1.1580071. S2CID 15580641.
Oeckl, Robert (2003). "Generalized lattice gauge theory, spin foams and state sum invariants". Journal of Geometry and Physics. 46 (3–4): 308–354. arXiv:hep-th/0110259. Bibcode:2003JGP....46..308O. doi:10.1016/S0393-0440(02)00148-1. S2CID 13226932.
Baez, John C. (1996). "Spin Networks in Gauge Theory". Advances in Mathematics. 117 (2): 253–272. arXiv:gr-qc/9411007. doi:10.1006/aima.1996.0012. S2CID 17050932.
원샤오강 "다체계의 수량장 이론 - 소리의 기원에서부터 빛과 페르미온의 기원까지," [1].
Major, Seth A. (1999). "A spin network primer". American Journal of Physics. 67 (11): 972–980. arXiv:gr-qc/9905020. Bibcode:1999AmJPh..67..972M. doi:10.1119/1.19175. S2CID 9188101.

책들

G. E. Stedman, Cambridge University Press, 1990년 그룹 이론의 다이어그램 기법.
프레드랙 씨비타노비치, 그룹 이론: 버드트랙스, 리즈, 엑설런트 그룹, 프린스턴 대학교 출판부, 2008.

[Penrose71-1] R. 펜로스(1971a), T. 바스틴(ed.), 양자 이론 및 비욘드(Beyond), 캠브리지 대학 출판부의 "사각형 모멘텀: 콤비네이터 스페이스타임에 대한 접근법" (이 논문은 존 C에서 온라인으로 볼 수 있다. Baez의 웹사이트) 및 R.Penrose(1971b), D. J. A.의 "부차원의 텐서 적용".웨일스(ed.), 결합 수학 및 응용 프로그램(Proc).콘프, 옥스포드, 1969), 학술지, 페이지 221–244, esp. 241 (후자 논문은 1969년에 발표되었으나 1971년에 로저 펜로즈에 따르면: I. 로빈슨, 비브립폴리스, 나폴리 1987년 명예의 권인 중력과 기하학에 관하여)에서 출판되었다.

[1]

v t 로저 펜로즈
책들	황제의 새로운 마음 (1989년) 마음의 그림자(1994) 현실로 가는 길(2004) 시간 주기(2010년) 우주의 새로운 물리학의 패션, 믿음, 판타지 (2016)
공동독서	공간과 시간의 특성 (Stephen Hawking과 함께)(1996) The Large, the Small and Human Mind (Abner Shimony, Nancy Cartwright, Stephen Hawking과 함께) (1997년) White Mars 또는 The Mind Set Free (Brian W와 함께) 알디스)(1999년)
학술작품	상대성에서의 미분위상 기법(1972) 스피너와 공간-시간: 제1권, 2-스파이너 미적분 및 상대론적 필드 (볼프강 린들러 포함) (1987년) Space-Time: Volume 2, Space-Time 기하학의 Spinor 및 Twistor 방법 (Wolfgang Rindler 포함) (1988)
개념	트위스터 이론 스핀 네트워크 추상지수 표기법 블랙홀 폭탄 스페이스타임의 기하학 우주 검열 웨일 곡률 가설 펜로스 불평등 양자역학의 펜로즈 해석 무어-펜로즈 역 뉴먼-펜로스 형식주의 펜로즈 도표 펜로스-호킹 특이점 이론들 펜로즈 부등식 펜로즈 공정 펜로즈 타일링 펜로즈 계단 펜로즈 그래픽 표기법 펜로즈 변환 펜로스-테렐 효과 조정된 목표 감소 /펜로스-루카스의 주장 펠릭스 실험 갇힌 표면 안드로메다 역설 등차 순환 우주론
관련	리오넬 펜로즈(아버지) 올리버 펜로즈 (오빠) 조나단 펜로스 (형) 셜리 호지슨(누나) 존 베레스포드 레테스(할아버지) 조명 문제 양자마인드

Search