펜로즈 삼각형

Penrose triangle
펜로즈 삼각형

펜로즈 트라이바르,[1] 불가능한 트라이바르 또는 불가능한 [2]삼각형으로도 알려진 펜로즈 삼각은 원근법으로 묘사될 수 있지만, 고체 물체로 존재할 수 없는 물체로 구성된 착시 현상인 삼각 불가능한 물체이다.그것은 1934년 [3]스웨덴의 예술가 오스카 로이터베드에 의해 처음 만들어졌다.로이터베르트와는 별개로, 이 삼각형은 1950년대에 정신과 의사 리오넬 펜로즈와 그의 아들인 저명한 노벨 수학자 로저 펜로즈가 고안하고 대중화했는데, 그는 이 삼각형을 "순수한 [4]형태로는 불가능"이라고 묘사했다.그것은 M. C. 에셔의 작품에서 두드러지게 나타나는데, 그의 초기 불가능한 사물에 대한 묘사는 부분적으로 영감을 주었다.

묘사

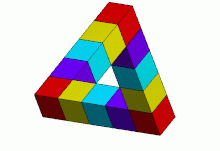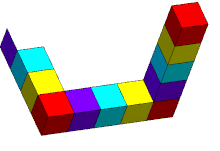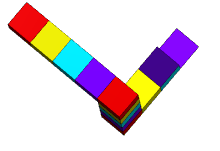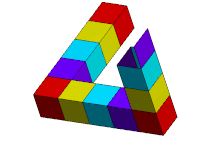
회전하는 펜로즈 삼각형 모형으로 착시현상을 보여줍니다.착시 순간 직각으로 연결된 한 쌍의 보라색 면(부분 막힘)이 있는 것처럼 보이지만 실제로는 평행한 면이며 부분 막힘 면은 외부가 아닌 내부이다.

트라이바르/삼각은 직사각형 단면의 직선 빔 세 개로 이루어진 입체 물체로, 이들이 형성하는 삼각형의 정점에서 직각으로 만나는 것으로 보입니다.빔이 깨져 큐브 또는 큐보이드 형태로 형성될 수 있습니다.

이러한 성질의 조합은 일반 유클리드 공간에서는 어떤 3차원 물체로도 실현될 수 없다.이러한 물체는 특정 유클리드 [5]3-매니폴드에 존재할 수 있다.또한 3차원 입체 도형도 존재하며, 각 도형은 특정 각도에서 볼 때 이 페이지의 펜로즈 삼각형의 2차원 묘사와 동일하게 나타난다(예를 들어 호주 퍼스의 조각품을 묘사한 인접 이미지).'펜로즈 삼각형'이란 2차원 묘사나 불가능한 물체 자체를 가리킬 수 있다.

펜로즈 삼각형을 중심으로 선이 추적되면 4-루프 뫼비우스 띠가 [6]형성됩니다.

묘사

3D 프린터로 제작한 Reutersvérd Triangle 착시 현상입니다.그 상자들은 실제로는 오목하지만 볼록해 보인다.

M.C. 에셔의 석판화 폭포(1961)는 두 개의 긴 펜로즈 삼각형의 긴 변을 따라 지그재그로 흐르는 물길을 묘사하고 있으며, 그래서 그것은 시작보다 2층 높게 끝나게 된다.결과적으로 생긴 폭포는 양쪽 삼각형의 짧은 변을 형성하며 물레방아를 찧는다.에셔는 바퀴가 계속 돌아가도록 하기 위해서는 증발을 보상하기 위해 가끔 물을 추가해야 한다고 지적합니다.

조각품

  • Impossible triangle sculpture as an optical illusion, East Perth, Western Australia

    착시현상으로서의 불가능한 삼각형 조각, 웨스트오스트레일리아주 이스트 퍼스

  • Impossible Triangle sculpture, Gotschuchen, Austria

    오스트리아 고트슈첸의 임파서블 트라이앵글 조각상

  • Real Penrose Triangle, Stainless Steel, by W.A.Stanggaßinger, Wasserburg am Inn, Germany. This type of impossible triangle was first created in 1969 by the Soviet kinetic artist Vyacheslav Koleichuk.[7]

    진짜 펜로즈 삼각지, 스테인리스 스틸, W.A.의독일 바세르부르크 암 인의 스탕가신저.이런 종류의 불가능한 삼각형은 1969년 소련의 운동 예술가인 Vyacheslav Koleichuk에 [7]의해 처음 만들어졌다.

「 」를 참조해 주세요.

레퍼런스

  1. ^ Pappas, Theoni (1989). "The Impossible Tribar". The Joy of Mathematics: Discovering Mathematics All Around You. San Carlos, California: Wide World Publ./Tetra. p. 13.
  2. ^ Brouwer, James R.; Rubin, David C. (June 1979). "A simple design for an impossible triangle". Perception. 8 (3): 349–350. doi:10.1068/p080349.
  3. ^ Ernst, Bruno (1986). "Escher's impossible figure prints in a new context". In Coxeter, H. S. M.; Emmer, M.; Penrose, R.; Teuber, M. L. (eds.). M. C. Escher Art and Science: Proceedings of the International Congress on M. C. Escher, Rome, Italy, 26–28 March, 1985. North-Holland. pp. 125–134. 특히 131페이지를 참조해 주세요.
  4. ^ Penrose, L. S.; Penrose, R. (February 1958). "Impossible objects: a special type of visual illusion". British Journal of Psychology. 49 (1): 31–33. doi:10.1111/j.2044-8295.1958.tb00634.x. PMID 13536303.
  5. ^ Francis, George K. (1988). "Chapter 4: The impossible tribar". A Topological Picturebook. Springer. pp. 65–76. doi:10.1007/978-0-387-68120-7_4. ISBN 0-387-96426-6. 특히 68쪽을 참조하십시오. 프랜시스는 이 관찰을 존 스틸웰의 탓으로 돌립니다.
  6. ^ Gardner, Martin (August 1978). "Mathematical Games: A Möbius band has a finite thickness, and so it is actually a twisted prism". Scientific American. 239 (2): 18–26. JSTOR 24960346.
  7. ^ Федоров, Ю. (1972). "Невозможное-Возможно". Техника Молодежи. 4: 20–21.

외부 링크