수학적 형태학

수학적 형태학(MM)은 집합 이론, 격자 이론, 위상, 무작위 함수에 기초하여 기하학적 구조의 분석과 처리를 위한 이론과 기법이다. MM은 디지털 영상에 가장 일반적으로 적용되지만, 그래프, 표면 메쉬, 솔리드, 그리고 많은 다른 공간 구조에서도 사용될 수 있다.

MM은 크기, 형태, 볼록도, 연결성, 지오데틱 거리 등의 위상학적, 기하학적 연속 공간 개념을 연속 공간과 이산 공간 모두에 도입했다. MM은 또한 형태학적 이미지 처리의 기초로서, 위의 특징에 따라 이미지를 변환하는 연산자 집합으로 구성되어 있다.

기본적인 형태론적 연산자는 침식, 팽창, 개폐다.

MM은 원래 이진 영상에 대해 개발되었으며, 이후 그레이스케일 기능과 영상에까지 확장되었다. 이후 격자를 완성하기 위한 일반화는 오늘날 MM의 이론적 토대로서 널리 받아들여지고 있다.

역사

수학적 형태학은 1964년 프랑스 파리 에콜 데 마인즈 드 파리의 조르주 마테론과 장 세라의 공동 연구로 개발되었다. 매더론은 세라 박사의 박사논문을 감독하여 얇은 단면으로부터 광물특성의 계량화에 전념하였고, 이 연구는 새로운 실용적 접근과 더불어 적분 기하학 및 위상에서의 이론적 진보를 이끌어냈다.

1968년 프랑스 폰테인블라우에 있는 에콜 데 마인즈 드 파리에 의해 마테론과 세라가 이끄는 '센터 드 모폴로니 마테마티크'가 설립되었다.

1960년대와 1970년대의 나머지 기간 동안 MM은 기본적으로 이진 이미지를 처리하고 세트로 처리하며 많은 수의 이진 연산자와 기법을 생성했다. 뺑소니 변형, 팽창, 침식, 개방, 폐쇄, 과립측정, 얇아짐, 골격화, 궁극적 침식, 조건부 이등분자 등. 새로운 이미지 모델을 바탕으로 무작위적인 접근법도 개발되었다. 그 시기의 대부분의 작품은 퐁텐블라우에서 개발되었다.

1970년대 중반부터 1980년대 중반까지 MM은 그레이스케일 기능과 이미지로 일반화되었다. 이러한 일반화는 주요 개념(확장, 침식 등)을 기능까지 확장하는 것 외에도 형태학적 그라데이션, 상단 모자 변환, 유역(MM의 주 분할 접근법)과 같은 새로운 연산자를 산출했다.

1980년대와 1990년대에 MM은 여러 나라의 연구 센터들이 이 방법을 채택하고 조사하기 시작하면서 더 넓은 인정을 받았다. MM은 많은 영상 문제와 어플리케이션에 적용되기 시작했다.

1986년, 세라는 MM을 더욱 일반화하여 이번에는 완전한 격자를 기초로 한 이론적 틀에 이르렀다. 이러한 일반화는 이론에 유연성을 가져와서, 색 이미지, 비디오, 그래프, 메쉬 등을 포함한 훨씬 더 많은 수의 구조에 그것의 적용을 가능하게 했다. 동시에 매더론과 세라는 새로운 격자틀을 바탕으로 형태학적 필터링 이론을 공식화하기도 했다.

1990년대와 2000년대에도 연결과 평준화의 개념을 포함해 이론적 진보가 더욱 진전되었다.

1993년 스페인 바르셀로나에서 제1회 수학 형태학 국제 심포지엄(ISMM)이 열렸다. 이후 ISMM은 2-3년마다 다음과 같이 구성된다. 프랑스 퐁텐블로(1994) 미국 애틀랜타(1996); 네덜란드 암스테르담(1998); 팔로 알토, CA, 미국(2000); 호주 시드니(2002); 프랑스 파리(2005) 브라질 리우데자네이루(2007); 네덜란드 그로닝언(2009); 내부(베르바니아), 이탈리아(2011년) 스웨덴 웁살라(2013년) 아이슬란드 레이캬비크(2015년)와 프랑스 폰테네블라우(2017년).

참조

• (Sera et al. (Eds.) 1994), pgs. 1-4의 피에르 토들레의 "소개".
• (세라 외 연구진 (Eds.) 1994), pgs.369-374에서 장 세라의 "부록 A: 'Centre de Morphologie Mathématique, 개요"를 인용했다.
• 2005년 (Ronse et al. (Eds.)의 "Foreword"

이항 형태학

이진 형태학에서 이미지는 일부 차원 d에 대해 유클리드 공간 $R{\displaystyle {\mathbb{}}^{}}$ d ${\$ 또는$$ 정수 격자 Z ${\displaystyle {}^{}}$ ${\$의 하위 집합으로 간주된다.

구조요소

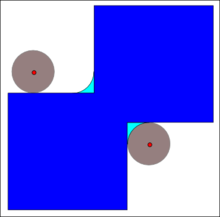
이항 형태학의 기본 개념은 단순하고 미리 정의된 형상으로 이미지를 조사하여 이 형상이 이미지 안에 있는 모양과 어떻게 맞거나 놓치는지에 대한 결론을 도출하는 것이다. 이 간단한 "프로브"는 구조 요소라고 불리며, 그 자체가 이진 이미지(즉, 공간이나 그리드의 부분집합)이다.

다음은 널리 사용되는 구조화 요소의 몇 가지 예(B로 표시됨):

• Let $E{\displaystyle }$= R ${\displaystyle {\mathrm{}}^{}}$ ${\$ E$=\mathb {R}^{2}}$ ;$$B는 반지름 r의 오픈 디스크로 원점을 중심으로 한다.
• Let $E{\displaystyle }$= ${\displaystyle {\mathbb{}}^{}}$ ${\displaystyle {\mathrm{}}^{}}$ ${\$ E$=\mathb {Z} ^{2$ B는 3× 3 제곱, 즉 B = {(-1, -1, 0), (-1, 0), (0, 0), (0, 0), (1, 0), (1, 0), (1, 0), (1, 0), (1, 0), (1, 1). 1). 1, 1, 1, 1, 1).
• Let $E{\displaystyle }$= ${\displaystyle {\mathbb{}}^{}}$ ${\displaystyle {\mathrm{}}^{}}$ ${\$ E$=\mathb {Z} ^{2$ B = {(-1, 0), (0, -1), (0, 1), (1, 0)이 주는 "십자"이다.

기본 연산자

기본 운영은 민코스키 덧셈과 강한 관련성이 있는 시프트 인바리넌트(번역 불변성) 연산자다.

E를 유클리드 공간 또는 정수 그리드로 하고, E의 이진 이미지 A로 한다.

침식

구조 요소 B에 의한 이진 이미지 A의 침식은 다음에 의해 정의된다.

${\displaystyle A\ominus B=\{z\in EB_{z}\subseteq A\}}$

여기서 B는_z 벡터 z에 의한 B의 번역이다$.$ 즉, $B{\displaystyle {}_{}}$ ${\displaystyle z_{}}$=${\displaystyle }${${\displaystyle b}$+ z ${\displaystyle \mid }$ ${\displaystyle b}$ ${\displaystyle \in }$ ${\displaystyle B}$ ${\displaystyle \}}$ ${\displaystyle B_{z}=\b+z\mid b\in B\}},$${\displaystyle \mathrm{}}$$,$ ${\displaystyle z}$ ${\displaystyle \forall$ z$\in E}.$

구조요소 B가 중심(예: B는 원반 또는 사각형)을 가지고 있고, 이 중심이 E의 원점에 위치하는 경우, B에 의한 A의 침식은 B가 내부로 이동할 때 B의 중심이 도달하는 지점의 중심점으로 이해할 수 있다. 예를 들어, 원점을 중심으로 한 면 10의 정사각형, 반지름 2의 원반에 의한 침식, 역시 원점을 중심으로 한 면 6의 정사각형이다.

B에 의한 A의 침식도 A${\displaystyle \mathrm{expression}}$ B =${\displaystyle \bigcap _{}}$ ${\displaystyle \underset{}{B}{}_{}}$∈ ${\displaystyle \underset{}{}{}_{}}$ ${\displaystyle B_{}}$ - b ${\$빅캡 _${b\in B}A_{-b}}}$라는 표현으로 주어진다$.$

응용 프로그램 예: 우리가 어두운 사진의 팩스를 받았다고 가정해보자. 모든 것이 피를 흘리는 펜으로 쓰여진 것 같다. 침식 과정을 거치면 두꺼운 선이 마르고 글자 "o" 안에 있는 구멍을 감지할 수 있을 것이다.

팽창

구조 요소 B에 의한 A의 확장은 다음과 같이 정의된다.

$B=\displaystyle A\oplus B=\bigcup _{b\in B}A_{b}.}$

팽창은 또한 ${\displaystyle A}$ ${\displaystyle \oplus }$B = ${\displaystyle B}$a${\displaystyle }$A = ${\displaystyle a}$ A =${\displaystyle \underset{a}{}}$ A${\displaystyle \underset{}{}{}_{}}$ A B ${\displaystyle a_{}}${\$displaystyle A\oplus$B=$B\oplus$ A$=\$blus A=\$bigcup _${a$}}}}$에 의해 주어진다$.$

B가 이전과 같이 원점에 중심이 있다면, B에 의한 확장은 B의 중심이 A 안으로 이동할 때 B가 커버하는 점의 중심점으로 이해할 수 있다. 위의 예에서 반경 2의 원반에 의한 면 10의 제곱은 면 14의 제곱이며, 모서리가 둥근 원점을 중심으로 한다. 둥근 모서리의 반지름은 2이다.

The dilation can also be obtained by ${\displaystyle A\oplus B=\{z\in E\mid (B^{s})_{z}\cap A\neq \varnothing \}}$, where B^s denotes the symmetric of B, that is, ${\displaystyle B^{s}=\{x\in E\mid -x\in B\}}$.

적용 예: 팽창은 침식의 이중 작동이다. 아주 가볍게 그려진 인물들은 "죽어 있다"면 두꺼워진다. 그것을 묘사하는 가장 쉬운 방법은 같은 팩스/텍스트가 더 두꺼운 펜으로 쓰여진다고 상상하는 것이다.

오프닝

A by B의 개방은 B에 의해 A가 침식된 후 B에 의해 그 결과의 영상이 확장됨으로써 얻어진다.

$(A\displaystyle A\circ B=(A\minus B)\oplus B.}$

개구부는 $또한{\displaystyle }$ A ${\displaystyle \circ }$ ${\displaystyle B}$ =${\displaystyle \underset{}{}}$ ${\displaystyle \underset{}{B_{}}}$ x ${\displaystyle \underset{}{{}_{}}}$ B ${\displaystyle x_{}}$ { B x ${\$A\$circ$ B$=\bigcup _{B_{x}\subseteq$A}$B_{x}}}}$에 의해 주어지는데$,$ 이는 이미지 A 안에 있는 구조 요소 B의 번역의 위치임을 의미한다. 측면 10의 제곱과 반지름 2의 원반이 구조 요소인 경우 개구부는 모서리가 둥근 측면 10의 제곱이며, 모서리 반경은 2이다.

응용 프로그램 예: 누군가가 비소금 종이에 메모를 썼다고 가정해 보자. 그리고 그 글씨는 마치 온몸에 털이 많은 작은 뿌리를 기르고 있는 것처럼 보인다. 개방은 본질적으로 외부의 작은 "헤어라인" 누출을 제거하고 본문을 복구한다. 부작용은 물건을 반올림하는 것이다. 날카로운 모서리가 사라지기 시작한다.

마감

A by B에 의한 폐쇄는 A b에 의한 확장에 의해 얻어지고, 그 결과 B에 의한 구조물의 침식에 의해 얻어진다.

$(A\displaystyle A\bullet B=(A\oplus B)\minus B.}$

The closing can also be obtained by ${\displaystyle A\bullet B=(A^{c}\circ B^{s})^{c}}$, where X^c denotes the complement of X relative to E (that is, ${\displaystyle X^{c}=\{x\in E\mid x\notin X\}}$). 위의 의미는 닫힘이 이미지 A 밖에 있는 구조화 요소의 대칭 번역 위치의 보완임을 의미한다.

기본 연산자의 속성

다음은 기본 이항 형태학 연산자(dilation, slimation, opening, open and closing)의 몇 가지 특성이다.

• 그들은 번역에 불변이다.
• They are increasing, that is, if ${\displaystyle A\subseteq C}$, then ${\displaystyle A\oplus B\subseteq C\oplus B}$, and ${\displaystyle A\ominus B\subseteq C\ominus B}$, etc.
• 팽창은 상쇄된다. ${\displaystyle A}$ ${\displaystyle \oplus }$ ${\displaystyle B}$= ${\displaystyle B}$ ${\displaystyle \oplus }$ ${\displaystyle A}$ ${\displaystyle A\oplus B=B\oplus A}$
• If the origin of E belongs to the structuring element B, then ${\displaystyle A\ominus B\subseteq A\circ B\subseteq A\subseteq A\bullet B\subseteq A\oplus B}$.
• The dilation is associative, i.e., ${\displaystyle (A\oplus B)\oplus C=A\oplus (B\oplus C)}$. Moreover, the erosion satisfies ${\displaystyle (A\ominus B)\ominus C=A\ominus (B\oplus C)}$.
• 침식과 ${\displaystyle \mathrm{팽창}}$은 이중성 $A{\displaystyle }$⊕ B${\displaystyle }$= ${\displaystyle ({}^{}}$ ${\displaystyle c^{}}$ ${\displaystyle {}^{}}$ B ${\displaystyle s^{}{}^{}}$) ${\displaystyle c^{}}$ ${\$ B$^{s}}}}}}}}{c}}}}}}$을 만족한다$.$
• 개폐는 이중성 $A{\displaystyle }$ ${\displaystyle \bullet }$ ${\displaystyle B}$=${\displaystyle }$(${\displaystyle {}^{}}$ ${\displaystyle c^{}}$ ${\displaystyle {}^{}}$ ${\displaystyle B^{}}$ ${\displaystyle {}^{}{}^{}}$) ${\displaystyle c^{}}$ ${\$ B$=(A^{c}\ccc^{s}}}}}}}}}{c}}}}}$을 만족한다$.$
• 확장은 세트 유니언에 대해 분배된다.
• 침식은 정해진 교차로에 분산되어 있다.
• 팽창은 다음과 같은 의미에서 침식의 유사역이며, 그 반대의 경우도 마찬가지다. ${\displaystyle A}$ ${\displaystyle \subseteq }$(${\displaystyle C}$ ${\displaystyle \ominus }$ B$){\displaystyle A\subseteq (C\inus$ B$)}$ 만약${\displaystyle }$(${\displaystyle A}$ ${\displaystyle \oplus }$ ${\displaystyle B}$) ${\displaystyle \subseteq }$ ${\displaystyle C}$ ${\displaystyle (A\oplus B)\subseteq C}$이$($가) 될 경우에만.
• 개폐하는 것은 단조로운 일이다.
• 개구부는 반격력, ${\displaystyle 즉}$ $A{\displaystyle }$ ${\displaystyle \circ }$ B ${\displaystyle \subseteq }$ ${\displaystyle A}$ ${\displaystyle$ A$\circle B\subseteq A}$이며$,$ 닫힘은 $A{\displaystyle }$ ${\displaystyle \subseteq }$ ${\displaystyle A}$ ${\displaystyle \bullet }$ ${\displaystyle B}$ ${\displaystyle A\subseteq A\bullet B}$이다$.$

기타 연산자 및 도구

• 적중 또는 결측 변환
• 가지치기 변환
• 형태학적 골격
• 재구성별 필터링
• 궁극의 에로션과 조건부 이등분자
• 그란울로메트리
• 측지 거리 함수

그레이스케일 형태학

In grayscale morphology, images are functions mapping a Euclidean space or grid E into ${\displaystyle \mathbb {R} \cup \{\infty ,-\infty \}}$, where ${\displaystyle \mathbb {R} }$ is the set of reals, ${\displaystyle \infty }$ is an element larger than any real number, and ${\displaystyle -\infty$$}$은(는) 어떤 실수보다 작은 원소다$$.

그레이스케일 구조요소는 또한 "구조함수"라고 불리는 같은 형식의 기능이다.

f(x)로 이미지를 나타내고 b(x)로 구조화 함수를 나타내며, b로 f의 그레이스케일 확장은 다음과 같다.

${\displaystyle (f\oplus b)(x)=\sup _{y\in E}[f(y)+b(x-y)],}$

여기서 "supp"은 우월감을 의미한다.

마찬가지로 b에 의한 f의 침식은 다음과 같이 주어진다.

${\displaystyle (f\minus b)(x)=\inf _{y\inf E}[f(y)-b(y-x)],}$

여기서 "inf"는 최소치를 의미한다.

이항 형태학에서와 마찬가지로, 개구부와 닫힘은 각각 다음과 같이 주어진다.

$f\displaystyle f\b=(f\ominus b)\oplus b,}$

$f\displaystyle f\b=(f\oplus b)\minus b.}$

평면 구조화 기능

형태학적 응용에서 평평한 구조화 요소를 사용하는 것이 일반적이다. 평면 구조화 함수는 형태의 함수 b(x)이다.

${\displaystyle b(x)={\begin{case}0,&x\in B,\\-\inflt >{otherwise},\case}}}$

여기서 $B{\displaystyle }$ ${\displaystyle \subseteq }$ ${\displaystyle E}$ ${\displaystyle B\subseteq$ E$\}.$

이 경우 팽창과 침식은 크게 단순화되며, 각각 다음과 같이 주어진다.

${\displaystyle (f\oplus b)(x)=\sup _{z\in B^}f(x+z),}$

${\displaystyle (f\minus b)(x)=\inf _{z\in B}f(x+z)}$

경계 이산형 케이스(E는 격자형이고 B는 경계형)에서, 우월성과 최소 연산자를 최대와 최소로 대체할 수 있다. 따라서 팽창과 침식은 이동 창(구조화 기능 지지대 B의 대칭) 내의 최대값을 반환하고, 침식은 이동 창 B 내의 최소값을 반환하는 주문 통계 필터의 특정한 경우다.

평면 구조 요소의 경우 형태학 연산자는 수치 값에 관계없이 픽셀 값의 상대적 순서에만 의존하므로 특히 광 전달 기능을 알 수 없는 이진 영상과 그레이스케일 영상의 처리에 적합하다.

기타 연산자 및 도구

• 형태학적 구배
• 상단 모자 변환
• 유역 알고리즘

이들 연산자를 결합하면 피쳐 검출, 이미지 분할, 이미지 선명화, 이미지 필터링, 분류 등 많은 이미지 처리 작업에 대한 알고리즘을 얻을 수 있다. 이 선을 따라 연속형 형태학도^[1] 살펴봐야 한다.

전체 격자의 수학적 형태학

완전 격자는 부분적으로 정렬된 집합으로, 모든 부분 집합은 최소값과 우월성을 가진다. 특히 최소한의 요소와 가장 큰 요소(또한 "유니버스"를 나타낸다)를 포함하고 있다.

부착물(부식 및 침식)

let${\displaystyle }$( ${\displaystyle L}$ ,${\displaystyle \le }$) ${\displaystyle (L,\leq )}$은(는) 각각 $\wedge {\displaystyle }$ ${\displaystyle \wedge }$과(는) $\vee {\displaystyle }$ ${\displaystyle \ve$로 상징되는 최소와 우월성을 가진 완전한 격자가 된다$$. 그것의 우주와 최소 원소는 각각 U와${\displaystyle \mathrm{}}$and ${\displaystyle \emptyet }$로 상징된다$.$ 더구나${\displaystyle }${${\displaystyle {Xi}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle \{X_{i}\}}}$을(를) L의 요소 집합으로 두도록$$ 한다.

확장은 $\Delta {\displaystyle }$: L${\displaystyle }$→ ${\displaystyle L}$ ${\displaystyle \delta \delta$\colon L\rightarrow $L}$ 연산자 Δ : ${\displaystyle L}$ → L {\displaystyle \delta L\colon L$\rightarrow$ L}이며$$, 최소 원소를 보존한다 예:

• ${\displaystyle \underset{}{\bigvee }}$ ${\displaystyle \underset{}{i}}$ ${\displaystyle \underset{}{}}$( ${\displaystyle X_{}}$ ${\displaystyle {}_{}}$)${\displaystyle }$= ${\displaystyle \Delta }$ (${\displaystyle \underset{}{}{\delta }_{}}$ i ${\displaystyle \underset{}{X}}$ i${\displaystyle {}_{}}$) ${\$
• ${\displaystyle \Delta }$ (${\displaystyle \mathrm{\varnothing }}$ )${\displaystyle }$= ${\displaystyle \mathrm{\varnothing }}$ ${\displaystyle \delta (\emptyet )=\emptyset$ $\}.$

침식은 최소치 이상으로 분포하고 우주를 보존하는$$ 모든 연산자${\displaystyle \epsilon }$ : ${\displaystyle L}$→ L ${\displaystyle \varepsilon \colon L\rightarrow L}$이다. 예:

• ${\displaystyle \underset{}{\bigwedge }}$ ${\displaystyle \underset{}{i}}$ ${\displaystyle \underset{}{}}$( ${\displaystyle {Xi}_{}}$)${\displaystyle }$= ${\displaystyle \epsilon }$ ${\displaystyle (\bigwedge \underset{}{}}$ i ${\displaystyle X_{}}$ i${\displaystyle {}_{}}$) ${\$ri$}\right$ ,
• ${\displaystyle \epsilon }$( ${\displaystyle U}$)${\displaystyle }$= ${\displaystyle U}$ ${\displaystyle \varepsilon (U)=U$

확장과 에로스가 갈루아 연결부를 형성한다. 즉, 모든 팽창 $\Delta {\displaystyle }$ ${\displaystyle \delta }$에 대해 충족되는$$ 하나의 침식 $\epsilon {\displaystyle }$ ${\displaystyle \var렙실론 }$이(가) 있다$$.

$\displaystyle X\leq \varepsilon (Y)\왼쪽 오른쪽 화살표 \delta (X)\leq Y}$

모든 $X{\displaystyle }$, ${\displaystyle Y}$ ${\displaystyle \in }$ ${\displaystyle L}$ ${\displaystyle X,Y\in L}$에 대해$.$

마찬가지로, 모든 침식에 대해 위의 연결을 만족시키는 유일한 팽창이 하나 있다.

또한 두 측정 시스템이 연결을 만족하면 $\Delta {\displaystyle }$ ${\displaystyle \delta }$이(가) 확장되어야 하며$$, $\Delta {\displaystyle }${\$displaystyle \varepsilon }$이(가) 침식되어야 한다.

위의 연결을 만족시키는 에로션과 팽창의 쌍을 "접합"이라고 하며, 침식은 팽창의 부차적 침식이라고 하며, 그 반대의 경우도 마찬가지라고 한다.

개폐

모든$$ 부속물$({\displaystyle \epsilon }$ ,${\displaystyle \Delta }$) ${\displaystyle (\varipsilon ,\delta$)에 대해$,$ 형태학적 개구부${\displaystyle \gamma }$ : ${\displaystyle L}$→ L ${\displaystyle \gamma \colon L}$ 및 형태학적$$ 폐쇄${\displaystyle }$: : $L{\displaystyle }$→ ${\displaystyle L}$ → L ${\displaysty \colon L}$과 같이 정의된다$.$

$\displaystyle \property \varepsilon ,}$

$\displaystyle \phi =\varepsilon \pair.}$

형태학적 개방과 폐쇄는 대수적 개방(또는 단순 개방)과 대수적 폐쇄(또는 단순 폐쇄)의 특정한 경우다. 대수적 개구부는 L의 연산자로, 공전성, 증가, 반증가성이다. 대수학적 폐쇄는 L에서 공전하고, 증가하고, 광범위한 연산자를 의미한다.

특정 사례

바이너리 형태학은 격자 형태학의 특정한 경우로서, 여기서 L은 E(유클리드 공간 또는 격자)의 동력 집합이며, 즉 L은 E의 모든 하위 집합의 집합이며, $\le {\displaystyle }$ ${\displaystyle \leq$}은$$ 세트포함이다. 이 경우 최소는 교차로 설정, 우월성은 조합으로 설정된다.

Similarly, grayscale morphology is another particular case, where L is the set of functions mapping E into ${\displaystyle \mathbb {R} \cup \{\infty ,-\infty \}}$, and ${\displaystyle \leq }$, ${\displaystyle \vee }$, and ${\displaystyle \wedge }$, are the point-wise order, supremum, and infimum, resp…을 속여서 That is, is f and g are functions in L, then ${\displaystyle f\leq g}$ if and only if ${\displaystyle f(x)\leq g(x),\forall x\in E}$; the infimum ${\displaystyle f\wedge g}$ is given by ${\displaystyle (f\wedge g)(x)=f(x)\wedge g(x)}$; and the supre${\displaystyle \mathrm{mom}}$ $f{\displaystyle }$∨ ${\displaystyle g}$ ${\displaystyle f\ve g}$은$({\displaystyle f}$ ${\displaystyle \vee }$ g${\displaystyle }$) (${\displaystyle x}$)${\displaystyle }$= ${\displaystyle f}$(${\displaystyle x}$ )${\displaystyle \vee }$ g ${\displaystyle (f\ve g)(x)=f(x)\ve g(x)}$에 의해 주어진다$$$.$

참고 항목

• H-maxima 변환

메모들

참조

• 장 세라의 이미지 분석과 수학적 형태학, ISBN0-12-637240-3(1982)
• 이미지 분석과 수학적 형태학, 제2권: 장 세라의 이론적 진보, ISBN 0-12-637241-1 (1988)
• Edward R의 형태학적 이미지 처리에 관한 소개 더거티, ISBN 0-8194-0845-X(1992)
• 형태학적 이미지 분석; 피에르 토들, ISBN 3-540-65671-5 (1999), 2판 (2003)의 원리 및 응용
• 수학적 형태학 및 신호 처리에 대한 응용, J. 세라 및 Ph Salembier (Eds.), ISMM'93, ISBN 84-7653-271-7 (1993)의 수학적 형태학 및 그 응용에 관한 제1차 국제 워크숍의 진행.
• Mathematical Morphology and Its Applications to Image Processing, J. Serra and P. Soille (Eds.), proceedings of the 2nd international symposium on mathematical morphology (ISMM'94), ISBN 0-7923-3093-5 (1994)
• Henk J.A.M.의 수학적 형태학과 이미지 및 신호 처리에 대한 적용 제4회 수학 형태학 국제 심포지엄(ISMM'98), ISBN 0-7923-5133-9 (1998)의 진행인 헤이즈만과 Jos B.T.M. Roerdink (Eds).
• Mathematical Morphology: 40 Years On, Christian Ronse, Laurent Najman, and Etienne Decencière (Eds.), ISBN 1-4020-3442-3 (2005)
• 수학적 형태학과 신호 및 이미지 처리에 대한 응용, 제럴드 J.F. 바논, 주니어 바레라, 울리스 M. 브라가-네토(Eds). 제8회 수학 형태학 국제 심포지엄(ISMM'07)의 진행, ISBN 978-85-17-00032-4(2007)
• 수학적 형태학: 이론에서 응용에 이르기까지, Laurent Najman과 Hugues Talbot (Eds. ISTE-Wiley. ISBN 978-1-84821-215-2(520쪽) 2010년 6월

외부 링크

• 장 세라(영어, 프랑스어, 스페인어)의 수학 형태학 온라인 과정
• 파리 광산학교 수학형태학센터
• 조르주 마테론과 장 세라의 수학 형태학 역사
• 피에르 토들레(Pierre Sandelle)의 수학적 형태학에 관한 뉴스레터인 형태학 다이제스트
• 이미지 처리 강의: 밴더빌트 대학교의 pdf 형식의 18개 강의 모음집. Alan Peters의 수학 형태학 강의 16-18
• 수학적 형태학: 컴퓨터 비전 강의에서 로빈 오웬스(Robyn Owens)의
• SMIL - 단순하지만 효율적인 형태 이미지 라이브러리(Ecole des Mines de Paris에서)
• 사용 가능한 SIMD 최적화 이미지 처리 라이브러리
• 자바 애플릿 데모
• 필터 : 무료 오픈 소스 이미지 처리 라이브러리
• 빠른 형태학적 에로스, 팽창, 개구부 및 폐쇄
• Matlab을 이용한 뉴런의 형태학적 해석