의료용 이미지 컴퓨팅
Medical image computing의료 이미지 컴퓨팅(MIC)은 컴퓨터 과학, 정보 공학, 전기 공학, 물리학, 수학 및 의학의 교차점에 있는 학제간 분야입니다.이 분야는 의료 이미지와 관련된 문제를 해결하기 위한 계산 및 수학적 방법과 생물의학 연구 및 임상 치료를 위한 그 사용을 개발한다.
총무성의 주요 목표는 의료 이미지에서 임상적으로 관련된 정보 또는 지식을 추출하는 것입니다.의료 영상 분야와 밀접하게 관련되어 있지만, MIC는 이미지 획득이 아닌 이미지의 컴퓨터 분석에 초점을 맞추고 있습니다.방법은 영상 분할, 영상 등록, 영상 기반 생리 모델링 등 [1]몇 가지 광범위한 범주로 그룹화할 수 있습니다.
데이터 폼
의료 영상 컴퓨팅은 일반적으로 일정한 x-y-z 공간 간격을 가진 균일하게 샘플링된 데이터에서 작동합니다(2D 영상 및 3D 볼륨, 일반적으로 영상이라고 함).각 샘플 포인트에서 데이터는 일반적으로 부호 없는 문자(8비트)에서 32비트 플로트까지의 형식이 드물지 않지만 부호 없는 쇼트(16비트) 및 부호 없는 쇼트(16비트)와 같은 통합 형식으로 표시됩니다.예를 들어, CT 획득은 방사선 농도 값을 수집하는 반면 MRI 획득은 T1 또는 T2 가중치 영상을 수집할 수 있습니다.시간에 따라 변하는 종방향 획득은 정기적인 시간 단계를 사용하여 영상을 획득하거나 획득하지 않을 수 있습니다.곡면 배열 초음파와 같은 양식으로 인한 부채꼴 영상도 일반적이며 처리하려면 다른 표현 및 알고리즘 기술이 필요합니다.다른 데이터 형식에는 획득 중 갠트리 기울기로 인한 전단 영상, 고급 생체역학 분석(예: 조직 변형, 혈관 이송, 뼈 이식)에 사용되는 6면체 및 4면체 형태와 같은 비정형 메시가 포함된다.
세그멘테이션
분할은 이미지를 다른 의미 있는 세그먼트로 분할하는 프로세스입니다.의료 영상촬영에서 이러한 세그먼트는 종종 다른 조직 클래스, 장기, 병리 또는 기타 생물학적으로 관련된 [2]구조에 해당합니다.의료 영상 분할은 저대비, 노이즈 및 기타 영상의 모호성으로 인해 어려워집니다.이미지 분할에는 많은 컴퓨터 비전 기법이 있지만 일부는 의료 이미지 컴퓨팅에 특별히 적용되었습니다.다음은 이 분야의 기술 샘플입니다. 구현은 임상의가 제공할 수 있는 전문지식에 의존합니다.
- Atlas 기반 세그멘테이션:많은 애플리케이션에서 임상 전문가는 여러 이미지에 수동으로 레이블을 지정할 수 있습니다. 보이지 않는 이미지를 분할하는 것은 이러한 수동 레이블이 지정된 교육 이미지에서 추정하는 것입니다.이 스타일의 방법은 일반적으로 아틀라스 기반 분할 방법이라고 합니다.파라메트릭 아틀라스 방법은 일반적으로 이러한 교육 영상을 단일 아틀라스 [3]영상으로 결합하는 반면, 비모수적 아틀라스 방법은 일반적으로 [4]모든 교육 영상을 개별적으로 사용합니다.Atlas 기반 방법은 일반적으로 Atlas 이미지를 보이지 않는 새로운 이미지에 정렬하기 위해 이미지 등록을 사용해야 합니다.
- 쉐이프 베이스 세그멘테이션:대부분의 방법에서는 주어진 구조물에 대한 템플릿 모양을 매개 변수화하며, 종종 경계를 따라 있는 제어점에 의존합니다.그런 다음 전체 모양이 변형되어 새 영상에 일치합니다.가장 일반적인 형상 기반 기법 중 두 가지는 활성 형상 모델과 활성 모양 [6]모델입니다.이 방법들은 매우 영향력이 있었고 비슷한 [7]모델을 만들어냈다.
- 이미지 기반 세그먼트화:활성 등고선 모델 및 [8]변형과 같은 일부 방법은 템플릿을 시작하고 이미지 데이터에 따라 모양을 세분화하는 동시에 통합 오류 측정을 최소화합니다.
- 인터랙티브 세그멘테이션:대화형 방법은 임상의가 시드 영역이나 분할할 영역의 대략적인 개요와 같은 정보를 제공할 수 있는 경우에 유용합니다.그런 다음 알고리즘은 임상의의 지침 유무에 관계없이 이러한 세분화를 반복적으로 미세화할 수 있다.페인트 브러시와 같은 도구를 사용하여 각 픽셀의 조직 클래스를 명시적으로 정의하는 수동 분할은 많은 이미징 애플리케이션의 기본 사양으로 유지됩니다.최근 피드백 제어 이론의 원칙이 세분화에 통합되어 사용자에게 훨씬 더 큰 유연성을 제공하고 [9]오류를 자동으로 수정할 수 있습니다.
- 주관적 표면 분할:이 방법은 이류-확산 [10]모델에 의해 지배되는 분할 함수의 진화 개념에 기초한다.개체를 분할하려면 분할 시드가 필요합니다(영상에서 개체의 대략적인 위치를 결정하는 시작 지점).이것에 의해, 초기 분할 함수를 구축한다.주관적 표면법의 배후에 있는 아이디어는 시드 위치가 이 분할 함수의 형태를 결정하는 주요 요소라는 것이다.
그러나 위의 범주와 유사한 영상 분할 방법에는 몇 가지 다른 분류가 있습니다.또, 다른 그룹은,[14] 방법의 편성에 근거해 「하이브리드」라고 분류할 수 있습니다.
등록.
이미지 등록은 이미지의 [15][16][17][18]올바른 정렬을 검색하는 프로세스입니다.가장 간단한 경우, 두 개의 영상이 정렬됩니다.일반적으로 한 이미지는 대상 이미지로 처리되고 다른 이미지는 소스 이미지로 처리됩니다. 소스 이미지는 대상 이미지와 일치하도록 변환됩니다.최적화 절차는 정렬의 현재 품질을 평가하는 유사성 값을 기반으로 원본 이미지의 변환을 업데이트합니다.이 반복 절차는 (로컬) 최적값이 나올 때까지 반복됩니다.예를 들어 구조 정보와 대사 정보를 결합하기 위한 CT 및 PET 영상 등록이 있습니다(그림 참조).
영상 등록은 다양한 의료 애플리케이션에서 사용됩니다.
- 시간적 변화를 연구하다.종적 연구는 질병 진행과 같은 장기적인 과정을 연구하기 위해 몇 달 또는 몇 년에 걸쳐 이미지를 획득합니다.시계열은 동일한 세션(초 또는 분) 내에서 획득한 영상에 해당합니다.그들은 인지 과정, 심장 변형 및 호흡을 연구하는 데 사용될 수 있다.
- 서로 다른 영상 모달리티의 보완 정보를 결합합니다.예를 들어 해부학적 정보와 기능적 정보의 융합이 있습니다.구조물의 크기와 모양은 양상에 따라 다르므로 선형 품질을 평가하는 것이 더 어렵습니다.이로 인해 상호 정보 [19]등 유사성 척도가 이용되고 있다.
- 피험자 집단을 특징짓는 것.대상 기관의 구조적 변동성에 따라 피험자 간 일대일 매핑이 존재하지 않을 수 있습니다.컴퓨터 [20]해부학에서 Atlas를 구성하려면 환자 간 등록이 필요합니다.여기서, 목적은 피험자에 걸친 장기의 해부학적 구조를 통계적으로 모델링하는 것입니다.
- 컴퓨터 보조 수술.컴퓨터 지원 수술에서는 CT 또는 MRI와 같은 수술 전 영상이 영상 안내 또는 항법을 용이하게 하기 위해 수술 중 영상 또는 추적 시스템에 등록됩니다.
이미지 등록을 수행할 때 고려해야 할 몇 가지 중요한 사항이 있습니다.
- 변환 모델.일반적으로는 강성, 아핀 및 변형 가능한 변환 모델을 선택할 수 있습니다.B-스플라인 및 박판 스플라인 모델은 매개 변수화된 변환 필드에 일반적으로 사용됩니다.비모수 또는 고밀도 변형 필드는 모든 그리드 위치에서 변위 벡터를 전달하므로 추가적인 정규화 제약이 필요합니다.변형 필드의 특정 클래스는 매끄러운 역방향의 반전 변환인 미분형식입니다.
- 유사성 메트릭입니다.거리 또는 유사함수는 등록품질을 정량화하기 위해 사용된다.이 유사성은 원본 영상 또는 영상에서 추출된 피쳐에서 계산할 수 있습니다.일반적인 유사성 측도는 거리 제곱합(SSD), 상관 계수 및 상호 정보입니다.유사성 측정의 선택은 영상이 동일한 촬영장비인지 여부에 따라 달라집니다. 획득 노이즈도 이 결정에 영향을 미칠 수 있습니다.예를 들어 SSD는 가우스 노이즈가 [21]있는 동일한 모달리티의 영상에 대한 최적의 유사성 척도입니다.그러나 초음파의 영상 통계는 가우스 노이즈와 상당히 다르므로 초음파 고유의 유사성 [22]측정이 도입되었다.다중 모달 등록에는 보다 정교한 유사성 측정이 필요합니다. 또는 구조 표현이나[23] 인접 [24][25]해부도 등록과 같은 다른 영상 표현을 사용할 수 있습니다.최근의[26] 연구는 CoMIR(Contrastive Multi-modal Image representations)라고 불리는 공유되고 고밀도 이미지 표현을 학습하기 위해 대조적인 코딩을 채택하여 기존 등록 방법이 충분히 유사한 이미지 구조의 부족으로 인해 종종 실패하는 멀티모달 이미지 등록을 가능하게 했다.멀티모달 등록 문제를 기능 기반뿐만 아니라 일반 강도 기반 등록 알고리즘을 적용할 수 있는 모노모달 등록 문제로 줄였습니다.
- 최적화 절차.연속 최적화 또는 이산 최적화가 수행됩니다.연속 최적화를 위해, 수렴 속도를 향상시키기 위해 구배 기반 최적화 기술을 적용한다.
시각화
시각화는 의료 이미지 컴퓨팅에서 몇 가지 중요한 역할을 합니다.과학적 시각화의 방법은 본질적으로 공간적 시간적인 의료 이미지를 이해하고 전달하는 데 사용된다.데이터 시각화 및 데이터 분석은 예를 들어 알고리즘 처리 중에 도출된 통계적 측정값을 평가할 때 비정형 데이터 형식에 사용됩니다.시각화 프로세스의 주요 특징인 데이터와의 직접 상호작용은 데이터에 대한 시각적 쿼리를 실행하고, 이미지에 주석을 달고, 분할 및 등록 프로세스를 안내하고, 데이터의 시각적 표현을 제어하기 위해 사용됩니다(조명 렌더링 특성 및 보기 매개 변수를 제어).시각화는 초기 탐색과 중간 및 최종 분석 결과를 전달하는 데 모두 사용된다.
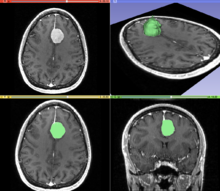
그림 "의료 영상의 시각화"는 1. 단면을 그레이 스케일 영상으로 표시, 2. 그레이 스케일 영상의 다시 포맷된 보기(이 예에서 시상 보기는 영상 획득의 원래 방향과 다른 방향) 및 3.의 여러 유형의 시각화를 보여 줍니다.동일한 데이터의 3D 볼륨 렌더링입니다.결절성 병변은 여러 표시에서 명확하게 볼 수 있으며 흰색 선으로 주석이 붙어 있습니다.
지도
다른 모양과 크기의 장기를 가진 사람 때문에 의료 이미지는 개인에 따라 크게 다를 수 있습니다.따라서 이러한 가변성을 설명하기 위해 의료 영상을 표현하는 것이 중요하다.의료 이미지를 표현하는 일반적인 방법은 하나 이상의 도표를 사용하는 것입니다.여기서 지도책이란 교육 데이터 [27][28]집합에서 학습한 매개 변수를 가진 이미지 집단의 특정 모델을 말합니다.
아틀라스의 가장 간단한 예는 보통 템플릿이라고 하는 평균 강도 영상입니다.그러나 지도책에는 로컬 이미지 통계 및 특정 공간 위치에 특정 라벨이 있을 확률과 같은 더 풍부한 정보도 포함될 수 있습니다.훈련 중에 사용되지 않는 새로운 의료 영상은 분할 및 그룹 분석과 같은 특정 애플리케이션에 맞게 조정된 아틀라스에 매핑할 수 있습니다.이미지를 아틀라스에 매핑하려면 일반적으로 이미지와 아틀라스를 등록해야 합니다.이러한 변형을 사용하여 의료 영상의 가변성을 해결할 수 있습니다.
단일 템플릿
가장 간단한 방법은 의료 영상을 단일 템플릿 이미지의 변형 버전으로 모델링하는 것입니다.예를 들어 해부학적 MRI 뇌 스캔은 공통 좌표로 모든 뇌 스캔을 나타내기 위해 MNI 템플릿에 매핑되는 경우가 많습니다.단일 템플릿 접근법의 주요 단점은 템플릿과 특정 테스트 이미지 사이에 큰 차이가 있는 경우 템플릿과 이미지를 서로 매핑하는 좋은 방법이 없을 수 있다는 것입니다.예를 들어 심각한 뇌 이상을 가진 환자의 해부학적 MRI 뇌 스캔(종양 또는 수술 절차)은 MNI 템플릿에 쉽게 매핑되지 않을 수 있습니다.
여러 템플릿
단일 템플릿에 의존하지 않고 여러 템플릿을 사용할 수 있습니다.이 아이디어는 이미지를 템플릿 중 하나의 변형 버전으로 표현하는 것입니다.예를 들어 건강한 모집단을 위한 템플릿 하나와 질병 모집단을 위한 템플릿 하나가 있을 수 있습니다.그러나 많은 응용 프로그램에서는 몇 개의 템플릿이 필요한지 명확하지 않습니다.계산상 비용이 많이 들지만 간단한 방법은 훈련 데이터 세트의 모든 이미지를 템플릿 이미지로 하여 새로운 이미지를 발견할 때마다 훈련 데이터 세트의 모든 이미지와 비교하는 것입니다.보다 최근의 접근 방식에서는 [30]필요한 템플릿의 수가 자동으로 검색됩니다.
통계 분석
통계적 방법은 의료 영상 분야와 최신 컴퓨터 비전, 기계 학습 및 패턴 인식을 결합합니다.지난 10년 동안 여러 개의 대규모 데이터 세트가 공개되었습니다(예: ADNI, 1000개의 기능적 Connectomes 프로젝트 참조). 부분적으로 다양한 기관과 연구 센터 간의 협업 때문입니다.이러한 데이터 크기 증가에는 임상 질문에 대처하기 위해 이미지의 미묘한 변화를 마이닝 및 검출할 수 있는 새로운 알고리즘이 필요합니다.이러한 임상 질문은 매우 다양하며 그룹 분석, 이미징 바이오마커, 질병 표현형 및 종적 연구를 포함합니다.
그룹 분석
그룹 분석에서는 두 개 이상의 코호트의 영상을 비교하여 질병으로 인한 이상을 검출하고 정량화하는 것이 목적이다.일반적으로 이러한 코호트 중 하나는 정상(대조군) 피험자로 구성되고 다른 하나는 비정상 환자로 구성됩니다.질병으로 인한 변화는 해부학의 비정상적인 변형으로 나타날 수 있다(복셀 기반 형태측정법 참조).예를 들어 뇌의 해마와 같은 피질하 조직의 수축은 알츠하이머병과 관련이 있을 수 있다.또한 양전자 방출 단층 촬영과 같은 영상 양식을 사용하여 생화학(기능) 활성의 변화를 관찰할 수 있습니다.
그룹 간 비교는 보통 복셀 수준에서 수행됩니다.따라서, 특히 신경 이미징에서 가장 인기 있는 전처리 파이프라인은 복셀 간의 대응 관계를 유지하기 위해 (Medical Image Registration)을 통해 데이터 세트의 모든 이미지를 공통 좌표 프레임으로 변환합니다.이러한 복셀별 대응이 주어진 경우, 가장 일반적인 빈도론 방법은 각 복셀에 대한 통계량(예: 각 그룹의 평균 복셀 강도)을 추출하고 통계 가설 테스트를 수행하여 귀무 가설이 지원되는지 여부를 평가하는 것입니다.귀무 가설은 일반적으로 두 개의 코호트가 동일한 분포에서 추출되므로 동일한 통계 특성을 가져야 한다고 가정합니다(예: 특정 복셀에 대해 두 그룹의 평균 값이 동일함).의료 영상에는 복셀이 다수 포함되어 있기 때문에 다중 비교 문제가 해결되어야 합니다.[31][32]그룹 분석 [33]문제를 해결하기 위한 베이지안 접근법도 있다.
분류
그룹 분석은 해부학과 기능에 대한 병리의 일반적인 영향을 정량화할 수 있지만, 대상 수준의 측정치를 제공하지 않으므로 진단을 위한 바이오마커로 사용할 수 없다(이미징 바이오마커 참조).반면에, 임상의는 종종 병리학의 조기 진단(즉,[34][35] 분류)과 질병의 진행 과정을 학습하는 데 관심이 있다(즉, 회귀).방법론적 관점에서, 현재 기법은 표준 기계 학습 알고리즘을 의료 영상 데이터 세트(예: 지원 벡터[37] 머신)에 적용하는 것에서부터 [38]현장의 요구에 적합한 새로운 접근방식을 개발하는 것까지 다양하다.주요 어려움은 다음과 같습니다.
- 작은 샘플 크기(치수의 저주): 대규모 의료 이미징 데이터 세트에는 수백에서 수천 개의 이미지가 포함되어 있지만, 일반적인 볼륨 이미지에서는 복셀 수가 수백만 개를 훌쩍 넘을 수 있습니다.이 문제의 해결 방법은 유익한 의미에서 기능의 수를 줄이는 것입니다(차원성 축소를 참조).이 문제를 해결하기 위해 몇 가지 비감독 [38][39][40][41]및 반감독 접근법이 제안되었다.
- 해석 가능성:임상의는 해부학의 어떤 부분이 이 질환의 영향을 받는지 알고 싶기 때문에 좋은 일반화 정확도가 항상 주된 목적은 아닙니다.따라서 결과의 해석성이 매우 중요하므로 영상 구조를 무시하는 방법은 선호되지 않습니다.특징 선택에 기초한 대체 방법이 제안되었다.[39][40][41][42]
클러스터링
이미지 기반 패턴 분류 방법은 일반적으로 질병의 신경학적 영향이 구별되고 잘 정의된다고 가정한다.항상 그렇지는 않을 수 있습니다.많은 의학적 조건의 경우, 환자 집단은 매우 이질적이며 하위 조건으로 더 이상 분류되지 않았다.또한 일부 질병(예: 자폐 스펙트럼 장애(ASD), 정신 분열증, 경도 인지 장애(MCI))는 경도 인지 장애에서 매우 뚜렷한 병리학적 변화에 이르기까지 연속적이거나 거의 연속적인 스펙트럼으로 특징지을 수 있다.이질적인 장애의 이미지 기반 분석을 용이하게 하기 위해 패턴 분류에 대한 방법론적 대안이 개발되었습니다.이러한 기술은 고차원 클러스터링 및 고차원 패턴 회귀로부터 아이디어를 빌려 주어진 모집단을 동종 하위 모집단으로 클러스터링한다.목표는 각 하위 모집단 내에서 질병에 대한 더 나은 양적 이해를 제공하는 것이다.
형상 분석
Shape Analysis(형상 분석)는 다양한 영상 양식에서 얻은 구조물의 기하학적 특성을 연구하는 의료 이미지 컴퓨팅 분야입니다.형태 분석은 건강 대 병리, 여성 대 남성, 젊은 대 노인 등 다양한 구조 집단 사이의 형태학적 변화를 정밀하게 찾을 수 있는 잠재력 때문에 최근 의학계의 관심이 높아지고 있다.형상 분석에는 형상 대응 및 통계 분석의 두 가지 주요 단계가 포함됩니다.
- 형상 대응은 삼각형 메시, 등고선, 점 세트 또는 체적 이미지로 표현되는 기하학적 형상 사이의 대응하는 위치를 계산하는 방법론이다.분명히 대응의 정의는 분석에 직접적인 영향을 미칠 것이다.대응 프레임워크에 대한 다양한 옵션 중에서 다음을 찾을 수 있습니다.해부학적 대응, 수동 랜드마크, 기능적 대응(즉, 동일한 신경 기능을 담당하는 뇌 형태 측정 궤적), 기하학적 대응, (영상 볼륨에 대한) 강도 유사성 등스펙트럼 형상 분석과 같은 일부 접근방식은 대응이 필요하지 않지만 형상 기술자를 직접 비교한다.
- 통계 분석은 해당 위치에서 구조 변화의 측정을 제공한다.
종적 연구
종적 연구에서는 동일한 인물을 반복적으로 촬영합니다.이 정보는 영상 분석 및 통계 모델링에 모두 통합할 수 있습니다.
- 종방향 화상 처리에서는, 통상, 피사체내의 템플릿으로부터 공통의 정보로, 개개의 시점의 분할 및 해석 방법을 통지해 정규화한다.이 정규화는 측정 노이즈를 줄이기 위해 설계되었으며, 따라서 감도와 통계적 파워를 증가시키는 데 도움이 됩니다.동시에 효과 크기를 안정적으로 유지하기 위해 과도한 정규화를 피해야 합니다.예를 들어 고도의 정규화를 통해 테스트 재시도 신뢰성이 향상될 수 있지만 그룹 간의 진정한 변화와 차이를 탐지할 수 있는 능력은 제한됩니다.종종 제한된 효과 크기 손실을 감수하면서 소음 감소를 최적화하는 트레이드오프가 필요하다.세로형 이미지 처리의 또 다른 공통적인 과제는 종종 의도하지 않은 처리 편향의 도입입니다.예를 들어 Follow up(팔로우업) 영상이 기준 영상에 등록되고 다시 샘플링되면 보간 아티팩트가 기준 영상이 아닌 Follow up(팔로우업) 영상에만 적용됩니다.이러한 아티팩트는 스플리어스 효과(일반적으로 세로 변화를 과대평가하여 필요한 표본 크기를 과소평가하는 편향)를 일으킬 수 있습니다.따라서 처리 편향을 피하기 위해서는 항상 점을 정확하게 동일하게 취급하는 것이 중요합니다.
- 종적 데이터의 사후 처리 및 통계 분석에는 일반적으로 반복 측정 분산 분석 또는 보다 강력한 선형 혼합 효과 모형과 같은 전용 통계 도구가 필요합니다.또한 신호의 공간 분포를 고려하는 것이 유리합니다.예를 들어, 피질 두께 측정에서는 피질 표면의 피질 내 및 인접 피질 내에서의 상관 관계를 확인할 수 있습니다. 이 사실은 통계적 힘을 증가시키는 데 사용될 수 있습니다.또한 종적 데이터를 분석하고 유의한 예측 변수를 결정하기 위해 사건 발생 시간(일명 생존) 분석이 자주 사용됩니다.
이미지 기반 생리 모델링
종래 의료용 이미지 컴퓨팅은 이미지 취득 시점 및 시점에서 이용 가능한 구조정보 또는 기능정보의 정량화와 융합에 대응하고 있었습니다.이와 관련하여, 이것은 기초적인 해부학적, 물리적 또는 생리학적 과정의 정량적 감지라고 볼 수 있다.그러나 지난 몇 년간 질병이나 치료 과정의 예측 평가에 대한 관심이 높아지고 있다.따라서 생체역학적 또는 생리학적 성질의 이미지 기반 모델링은 설명적 각도에서 예측적 각도로 이미지 컴퓨팅의 가능성을 확장할 수 있다.
STEP 연구 [44][45]로드맵에 따르면 가상생리학 인간(VPH)은 방법론적이고 기술적인 프레임워크로, 확립되면 인체를 하나의 복잡한 시스템으로 조사할 수 있게 된다.VPH 개념의 기초가 되는 국제생리학연합(IUPS)은 10년 이상 [46][47]IUPS Physicalome Project를 후원해 왔습니다.이것은 인간의 생리를 이해하기 위한 계산 프레임워크를 제공하기 위한 전 세계적인 공공 영역 노력이다.유전자 조절 네트워크, 단백질 경로, 통합 세포 기능, 조직 및 전체 장기 구조/기능 관계를 통해 유전자에서 전체 유기체에 이르는 모든 수준의 통합 모델을 개발하는 것을 목표로 한다.이러한 접근방식은 현재의 의학 관행을 변화시키는 것을 목표로 하고 있으며 컴퓨터 [48]의학이라는 새로운 시대를 뒷받침하고 있습니다.
이러한 맥락에서 의료 영상과 이미지 컴퓨팅은 인체 내 구조 및 기능 정보를 이미지화하고 정량화하고 융합하는 시스템과 방법을 제공하기 때문에 점점 더 중요한 역할을 한다.이 두 가지 광범위한 연구 영역에는 특정 주제를 나타내기 위한 범용 계산 모델의 변환이 포함되며, 따라서 개인화된 계산 [49]모델을 위한 길을 열어줍니다.영상을 통한 범용 계산 모델의 개별화는 세 가지 보완적인 방향으로 실현될 수 있습니다.
- 주제별 계산 영역(computer domain) 및 관련 하위 영역(표준 유형)의 정의
- (동적 및/또는 기능적) 이미징에 의한 경계 및 초기 조건의 정의
- 구조적 및 기능적 조직의 특성화.
또한 이미징은 인간과 동물 모델 모두에서 그러한 모델의 평가와 검증에 중추적인 역할을 하며, 진단 및 치료 애플리케이션 모두에서 모델을 임상 환경으로 변환하는 데에도 중추적인 역할을 한다.이 특정한 맥락에서 분자, 생물학적 및 임상 전 이미징은 분자, 세포, 조직 및 동물 모델의 기본 구조와 기능에 대한 추가 데이터 및 이해를 제공합니다. 이는 적절한 경우 인간의 생리학에 전달될 수 있습니다.
기본 및 임상 영역에서 이미지 기반 VPH/Physiome 모델의 적용 범위는 매우 넓습니다.대체로 새로운 가상 이미징 기술이 될 것으로 예상됩니다.관측 가능하지만 때로는 희박하고 일관성이 없는 멀티모달 영상과 생리학적 측정의 통합을 기반으로 더 많은, 종종 관찰할 수 없는 파라미터가 silico에서 촬영됩니다.계산 모델은 조사 중인 생리학 또는 병리생리학 과정의 기초 생물물리학, 생화학 또는 생물학적 법칙에 부합하는 방식으로 측정에 대한 해석을 발생시킨다.궁극적으로, 그러한 조사 도구와 시스템은 질병 과정, 질병 진화의 자연사, 그리고 약리학적 및/또는 중재적 치료 절차의 질병 과정에 대한 영향을 이해하는 데 도움이 될 것이다.
이미징과 모델링 사이의 교차 여과는 생리학과 일치하는 방식으로 측정의 해석을 넘어선다.의료기기 및 약리치료의 모델과 결합된 이미지 기반 환자 고유 모델링은 예측 영상으로 가는 길을 열어주며, 이를 통해 실리코에서 그러한 개입을 이해하고 계획하고 최적화할 수 있다.
의료 영상촬영의 수학적 방법
많은 정교한 수학적 방법이 의료 이미징에 들어갔으며, 이미 다양한 소프트웨어 패키지로 구현되었습니다.여기에는 확장, 분할 및 등록을 위한 PDE(Partial Differential Equiations) 및 곡률 중심 흐름은 다음과 같습니다.PDE를 채용하고 있기 때문에 GPGPU에서의 병렬화 및 구현이 가능합니다.이러한 기술 중 많은 것들이 최적의 제어에 대한 아이디어에서 영감을 얻었습니다.따라서 제어에서 나온 아이디어는 최근 대화형 방법, 특히 세분화로 발전하고 있습니다.게다가 노이즈와 보다 동적으로 변화하는 이미지를 위한 통계적 추정 기법의 필요성 때문에 Kalman[50] 필터와 입자 필터가 사용되었다.광범위한 참조 목록을 포함한 이러한 방법에 대한 조사는 [51]에서 확인할 수 있습니다.
모달리티 고유의 컴퓨팅
일부 이미징 모달리티는 매우 특수한 정보를 제공합니다.생성된 이미지는 일반 스칼라 이미지로 취급할 수 없으며 의료 이미지 컴퓨팅의 새로운 하위 영역을 생성할 수 없습니다.예를 들어 확산 MRI, 기능 MRI 등이 있습니다.
확산 MRI
확산 MRI는 분자의 확산 과정을 측정할 수 있는 구조 자기 공명 영상 촬영 방식입니다.확산은 특정 방향을 따라 자기장에 경사 펄스를 인가함으로써 측정된다.전형적인 취득에서는 균일하게 분포된 구배 방향의 세트를 사용하여 확산 가중치 부피 세트를 생성한다.또, 경사 펄스를 인가하지 않고, 같은 자기장하에서 무가중 볼륨을 취득한다.각 수집은 여러 볼륨과 관련되어 있기 때문에 확산 MRI는 의료용 이미지 컴퓨팅에서 다양한 고유한 문제를 야기하고 있습니다.
의학에서 확산 MRI에는 두 가지 주요 계산 목표가 있습니다.
- 확산성 등의 국소 조직 특성 추정
- 확산의 국지적 방향과 전역 경로의 추정.
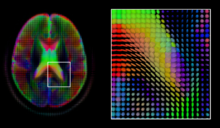
확산 [52]텐서, 3 × 3 대칭 정의 행렬은 이 두 가지 목표에 대한 간단한 해결책을 제공한다.정규 분포 국소 확산 프로파일의 공분산 행렬에 비례하므로, 이 행렬의 지배적인 고유 벡터는 국소 확산의 주요 방향이다.이 모델의 단순성 때문에 확산 텐서의 최대우도 추정은 각 위치에서 선형 방정식의 시스템을 독립적으로 푸는 것만으로 찾을 수 있다.단, 부피가 인접한 조직섬유를 포함하는 것으로 가정되므로 텐서의 [53]기초장소에 규칙성 조건을 부과함으로써 확산텐서 전체의 부피를 추정하는 것이 바람직할 수 있다.스칼라 값은 축삭섬유의 골수 이상화 또는 [55]부종의 존재와 같은 조직 특성을 간접적으로 측정하는 부분 이방성, 평균, 축방향 및 방사방향 확산성 등의 확산 텐서에서 추출할 수 있다.등록이나 세그멘테이션등의 표준 스칼라 화상 컴퓨팅 방법은, 그러한 스칼라치의 볼륨에 직접 적용할 수 있습니다.그러나 이러한 방법은 확산 텐서의 정보를 충분히 활용하기 위해 등록 및 [58][59]분할을 수행할 때 텐서 값 부피를 고려하도록 조정되었다.
부피의 각 위치에서 확산의 주요 방향이 주어지면 트랙토그래피로 [60]알려진 과정을 통해 확산의 전역 경로를 추정할 수 있다.그러나 확산 MRI의 분해능이 비교적 낮기 때문에 이러한 경로의 대부분은 한 곳에서 교차, 키스 또는 부채꼴이 될 수 있습니다.이 상황에서 확산 텐서의 단일 주방향은 국소 확산 분포에 적합한 모델이 아니다.이 문제에 대한 가장 일반적인 해결책은 보다 복잡한 모델을 사용하여 국소 확산의 여러 방향을 추정하는 것입니다.여기에는 확산 텐서,[61] Q-볼 이미징,[62] 확산 스펙트럼 이미징 및 섬유 방향 분포 함수의 [64][65]혼합물이 포함되며, 일반적으로 많은 구배 방향의 HARDI 획득이 필요하다.확산 텐서와 마찬가지로, 이러한 복잡한 모델에서 가치가 있는 볼륨은 등록[66][67][68] 및 [69]분할과 같은 이미지 컴퓨팅 방법을 적용할 때 특별한 처리가 필요합니다.
기능성 MRI
기능성 자기공명영상(fMRI)은 국소 혈류역학 또는 혈중 산소수준 의존신호(BOD)를 관찰하여 신경활동을 간접적으로 측정하는 의료 이미징 양식입니다.fMRI 데이터는 다양한 통찰력을 제공하며 대략 두 가지 범주로 나눌 수 있습니다.
- 과제 관련 fMRI는 실험 대상자가 일련의 시간적 실험 조건을 수행함에 따라 획득된다.블록 설계 실험에서 조건은 짧은 시간(예: 10초) 동안 존재하며 정지 기간과 교대로 이루어진다.사건 관련 실험은 무작위 자극 시퀀스에 의존하며 각 조건을 나타내기 위해 단일 시점을 사용한다.fMRI 관련 과제를 분석하기 위한 표준 접근법은 일반 선형 모델(GLM)이다.
- 실험 작업이 없을 때 정지 상태 fMRI를 획득합니다.전형적으로, 목적은 뇌의 본질적인 네트워크 구조를 연구하는 것이다.휴식 중에 이루어진 관찰은 부호화 또는 반사와 같은 특정 인지 과정과도 연결되어 있다.정지상태 fMRI에 대한 대부분의 연구는 fMRI 신호(LF-BOLD)의 저주파 변동에 초점을 맞추고 있습니다.중요한 발견에는 기본 네트워크, 포괄적인 [71]피질 파셀화 및 네트워크 [72]특성과 동작 파라미터의 링크 등이 있습니다.
기능성 신경 영상 데이터를 분석하는 데 사용되는 다양한 방법론이 있으며, 최선의 방법에 대한 합의가 이루어지지 않는 경우가 많습니다.대신 연구자들은 각 문제를 독립적으로 접근하고 적절한 모델/알고리즘을 선택합니다.이러한 맥락에서 신경과학, 컴퓨터 생물학, 통계학 및 기계학습 커뮤니티 간에 비교적 활발한 교류가 있다.주요 접근방식은 다음과 같습니다.
- 영상 데이터의 개별 복셀을 탐색하여 실험 조건과의 관계를 확인하는 대규모 일변량 접근법.주요 접근 방식은 일반 선형 모델(GLM)입니다.
- 다변량 및 분류기 기반 접근법은 종종 다중 복셀 패턴 분석 또는 다변량 패턴 분석으로 불리며 실험 조건에 대한 전역 및 잠재적으로 분산된 반응에 대한 데이터를 조사합니다.초기 접근법은 시각적 [73]자극에 대한 반응을 연구하기 위해 SVM(support vector machine)을 사용했다.최근 랜덤 포레스트 기반 지니 대비 또는 희박한 회귀 및 사전 학습과 같은 대체 패턴 인식 알고리즘이 탐색되었다.
- 기능적 연결성 분석은 영역 간의 상호작용을 포함한 뇌의 고유한 네트워크 구조를 연구합니다.그러한 연구의 대부분은 뇌를 구분하거나 행동 [76]측정과의 상관관계를 찾기 위해 휴식 상태 데이터에 초점을 맞추고 있다.과제별 데이터를 사용하여 뇌 영역 간의 인과 관계를 연구할 수 있습니다(예: 동적 인과 관계 매핑(DCM)).
대규모 피험자 집단으로 작업할 경우 공통 참조 프레임으로 개별 피험자를 정규화(등록)하는 것이 중요합니다.해부도(FSL, FreeSurfer, SPM)를 기반으로 정규화를 수행하기 위한 작업 및 도구가 있습니다.피사체 간의 공간적 가변성을 고려한 정렬은 보다 최근의 작업이다.예로는 fMRI 신호 [78]상관관계에 기초한 피질의 정렬, 태스크 또는 정지 상태 [79]데이터 모두에서 전역 기능 연결 구조에 기초한 정렬, 개별 복셀의 [80]자극 특정 활성화 프로파일에 기초한 정렬이 있다.
소프트웨어
의료용 이미지 컴퓨팅 소프트웨어는 IO, 시각화 및 상호작용, 사용자 인터페이스, 데이터 관리 및 계산을 제공하는 시스템의 복잡한 조합입니다.일반적으로 시스템 아키텍처는 알고리즘 개발자, 애플리케이션 개발자 및 사용자에게 서비스를 제공하기 위해 계층화됩니다.하위 계층은 기본 계산 기능을 제공하는 라이브러리 및/또는 툴킷이며, 상위 계층은 특정 의료 문제, 질병 또는 신체 시스템을 다루는 특수 애플리케이션입니다.
기타 주의사항
의료 이미지 컴퓨팅은 컴퓨터 비전 분야와도 관련이 있습니다.국제 사회인 MICCAI Society는 이 분야를 대표하여 연례 회의 및 관련 워크숍을 개최합니다.이 컨퍼런스의 진행은 Springer가 컴퓨터 사이언스 강의 노트 [81]시리즈에 게재하고 있습니다.2000년에 N.아야체와 J. 던컨은 [82]필드 상태를 검토했다.
「 」를 참조해 주세요.
레퍼런스
- ^ Perera Molligoda Arachchige, Arosh S.; Svet, Afanasy (2021-09-10). "Integrating artificial intelligence into radiology practice: undergraduate students' perspective". European Journal of Nuclear Medicine and Molecular Imaging. doi:10.1007/s00259-021-05558-y. ISSN 1619-7089.
- ^ Forghani, M.; Forouzanfar, M.; Teshnehlab, M. (2010). "Parameter optimization of improved fuzzy c-means clustering algorithm for brain MR image segmentation". Engineering Applications of Artificial Intelligence. 23 (2): 160–168. doi:10.1016/j.engappai.2009.10.002.
- ^ J Gee; M Reivich; R Bajcsy (1993). "Elastically Deforming a Three-Dimensional Atlas to Match Anatomical Brain Images". Journal of Computer Assisted Tomography. 17 (1): 225–236. doi:10.1097/00004728-199303000-00011. PMID 8454749. S2CID 25781937.
- ^ MR Sabuncu; BT Yeo; K Van Leemput; B Fischl; P Golland (June 2010). "A Generative Model for Image Segmentation Based on Label Fusion". IEEE Transactions on Medical Imaging. 29 (10): 1714–1729. doi:10.1109/TMI.2010.2050897. PMC 3268159. PMID 20562040.
- ^ Cootes TF, Taylor CJ, Cooper DH, Graham J (1995). "Active shape models-their training and application". Computer Vision and Image Understanding. 61 (1): 38–59. doi:10.1006/cviu.1995.1004.
- ^ Cootes, T.F.; Edwards, G.J.; Taylor, C.J. (2001). "Active appearance models". IEEE Transactions on Pattern Analysis and Machine Intelligence. 23 (6): 681–685. CiteSeerX 10.1.1.128.4967. doi:10.1109/34.927467.
- ^ G. Zheng; S. Li; G. Szekely (2017). Statistical Shape and Deformation Analysis. Academic Press. ISBN 9780128104941.
- ^ R. Goldenberg, R. Kimmel, E. Rivlin, and M. Rudzsky (2001). "Fast geodesic active contours" (PDF). IEEE Transactions on Image Processing. 10 (10): 1467–1475. Bibcode:2001ITIP...10.1467G. CiteSeerX 10.1.1.35.1977. doi:10.1109/83.951533. PMID 18255491.
{{cite journal}}: CS1 maint: 여러 이름: 작성자 목록(링크) - ^ Karasev, P.; Kolesov I.; Chudy, K.; Vela, P.; Tannenbaum, A. (2011). Interactive MRI segmentation with controlled active vision. Proceedings of the Conference on Decision and Control. pp. 2293–2298. doi:10.1109/CDC.2011.6161453. ISBN 978-1-61284-801-3. PMC 3935399. PMID 24584213.
- ^ K. 미쿨라, N. 페이리에라스, M. 레메시코바, A.Sarti: 유한 볼륨 기술을 사용하여 일반화된 주관적 표면법에 의한 3D 태생 영상 분할.FVCA5 - 제5회 복합 어플리케이션 유한량에 관한 국제 심포지엄, 에르메스 퍼블, 파리 2008.
- ^ A. Sarti, G. Citti: 주관적 표면과 리만 평균 곡률 흐름 그래프.액타 수학코메니아 대학 (북미) 70 (2000), 85 ~103
- ^ A. Sarti, R. Malladi, J.A. Sethian:주관적 표면:누락된 경계를 완성하는 방법.검사님, Natl.학술원 과학부 12호, 97호(2000년), 6258~6263.
- ^ A. Sarti, R. Malladi, J.A. Sethian:주관적 표면:경계 완성을 위한 기하학적 모델, 국제 컴퓨터 비전 저널, mi 46, No. 3(2002), 201-221.
- ^ Ehsani Rad, Abdolvahab; Mohd Rahim Mohd Shafry; Rehman Amjad; Altameem Ayman; Saba Tanzila (May 2013). "Evaluation of Current Dental Radiographs Segmentation Approaches in Computer-aided Applications". IETE Technical Review. 30 (3): 210. doi:10.4103/0256-4602.113498. S2CID 62571134.
- ^ Lisa Gottesfeld Brown (1992). "A survey of image registration techniques". ACM Computing Surveys. 24 (4): 325–376. CiteSeerX 10.1.1.35.2732. doi:10.1145/146370.146374. S2CID 14576088.
- ^ J. Maintz; M. Viergever (1998). "A survey of medical image registration". Medical Image Analysis. 2 (1): 1–36. CiteSeerX 10.1.1.46.4959. doi:10.1016/S1361-8415(01)80026-8. PMID 10638851.
- ^ J. Hajnal; D. Hawkes; D. Hill (2001). Medical Image Registration. Baton Rouge, Florida: CRC Press.
- ^ Barbara Zitová; Jan Flusser (2003). "Image registration methods: a survey". Image Vision Comput. 21 (11): 977–1000. doi:10.1016/S0262-8856(03)00137-9. hdl:10338.dmlcz/141595.
- ^ J. P. W. Pluim; J. B. A. Maintz; M. A. Viergever (2003). "Mutual information based registration of medical images: A survey". IEEE Trans. Med. Imaging. 22 (8): 986–1004. CiteSeerX 10.1.1.197.6513. doi:10.1109/TMI.2003.815867. PMID 12906253. S2CID 2605077.
- ^ Grenander, Ulf; Miller, Michael I. (1998). "Computational anatomy: an emerging discipline". Q. Appl. Math. LVI (4): 617–694. doi:10.1090/qam/1668732.
- ^ P. A. Viola (1995). Alignment by Maximization of Mutual Information (Thesis). Massachusetts Institute of Technology.
- ^ C. Wachinger; T. Klein; N. Navab (2011). "Locally adaptive Nakagami-based ultrasound similarity measures". Ultrasonics. 52 (4): 547–554. doi:10.1016/j.ultras.2011.11.009. PMID 22197152.
- ^ C. Wachinger; N. Navab (2012). "Entropy and Laplacian images: structural representations for multi-modal registration". Medical Image Analysis. 16 (1): 1–17. doi:10.1016/j.media.2011.03.001. PMID 21632274.
- ^ Hill, Derek LG; Hawkes, David J (1994-04-01). "Medical image registration using knowledge of adjacency of anatomical structures". Image and Vision Computing. 12 (3): 173–178. CiteSeerX 10.1.1.421.5162. doi:10.1016/0262-8856(94)90069-8. ISSN 0262-8856.
- ^ Toth, Daniel; Panayiotou, Maria; Brost, Alexander; Behar, Jonathan M.; Rinaldi, Christopher A.; Rhode, Kawal S.; Mountney, Peter (2016-10-17). Registration with Adjacent Anatomical Structures for Cardiac Resynchronization Therapy Guidance. Statistical Atlases and Computational Models of the Heart. Imaging and Modelling Challenges (Submitted manuscript). Lecture Notes in Computer Science. pp. 127–134. doi:10.1007/978-3-319-52718-5_14. ISBN 9783319527178.
- ^ 피에로브스키, 베처, E., Ofverstett, J., Lu. J., 벨비, C., 린드블라드, J. 및 슬라도예(2020)CoMIR: 등록을 위한 대조적인 멀티모달 이미지 표현.신경 정보 처리 시스템의 발전 (p. 18433–18444)Curran Associates, Inc.
- ^ M. De Craene; A. B. d Aische; B. Macq; S. K. Warfield (2004). "Multi-subject registration for unbiased statistical atlas construction" (PDF). Proceedings of Medical Image Computing and Computer-Assisted Intervention 2004. Lecture Notes in Computer Science. 3216: 655–662. doi:10.1007/978-3-540-30135-6_80. ISBN 978-3-540-22976-6.
- ^ C. J. Twining; T. Cootes; S. Marsland; V. Petrovic; R. Schestowitz; C. Taylor (2005). "A unified information-theoretic approach to groupwise non-rigid registration and model building". Proceedings of Information Processing in Medical Imaging 2005. Lecture Notes in Computer Science. 19: 1–14. doi:10.1007/11505730_1. ISBN 978-3-540-26545-0. PMID 17354680.
- ^ "The MNI brain and the Talairach atlas".
- ^ M. Sabuncu; S. K. Balci; M. E. Shenton; P. Golland (2009). "Image-driven Population Analysis through Mixture Modeling". IEEE Transactions on Medical Imaging. 28 (9): 1473–1487. CiteSeerX 10.1.1.158.3690. doi:10.1109/TMI.2009.2017942. PMC 2832589. PMID 19336293.
- ^ J. Ashburner; K.J. Friston (2000). "Voxel-Based Morphometry – The Methods". NeuroImage. 11 (6): 805–821. CiteSeerX 10.1.1.114.9512. doi:10.1006/nimg.2000.0582. PMID 10860804. S2CID 16777465.
- ^ C. Davatzikos (2004). "Why voxel-based morphometric analysis should be used with great caution when characterizing group differences". NeuroImage. 23 (1): 17–20. doi:10.1016/j.neuroimage.2004.05.010. PMID 15325347. S2CID 7452089.
- ^ K.J. Friston; W.D. Penny; C. Phillips; S.J. Kiebel; G. Hinton; J. Ashburner (2002). "Classical and Bayesian Inference in Neuroimaging: Theory". NeuroImage. 16 (2): 465–483. CiteSeerX 10.1.1.128.8333. doi:10.1006/nimg.2002.1090. PMID 12030832. S2CID 14911371.
- ^ Yong Fan; Nematollah Batmanghelich; Chris M. Clark; Christos Davatzikos (2008). "Spatial patterns of brain atrophy in MCI patients, identified via high-dimensional pattern classification, predict subsequent cognitive decline". NeuroImage. 39 (4): 1731–1743. doi:10.1016/j.neuroimage.2007.10.031. PMC 2861339. PMID 18053747.
- ^ Rémi Cuingnet; Emilie Gerardin; Jérôme Tessieras; Guillaume Auzias; Stéphane Lehéricy; Marie-Odile Habert; Marie Chupin; Habib Benali; Olivier Colliot (2011). "The Alzheimer's Disease Neuroimaging Initiative, Automatic classification of patients with Alzheimer's disease from structural MRI: A comparison of ten methods using the ADNI database" (PDF). NeuroImage. 56 (2): 766–781. doi:10.1016/j.neuroimage.2010.06.013. PMID 20542124. S2CID 628131.
- ^ Y. Wang; Y. Fan; P. Bhatt P; C. Davatzikos (2010). "High-dimensional pattern regression using machine learning: from medical images to continuous clinical variables". NeuroImage. 50 (4): 1519–35. doi:10.1016/j.neuroimage.2009.12.092. PMC 2839056. PMID 20056158.
- ^ Benoît Magnin; Lilia Mesrob; Serge Kinkingnéhun; Mélanie Pélégrini-Issac; Olivier Colliot; Marie Sarazin; Bruno Dubois; Stéphane Lehéricy; Habib Benali (2009). "Support vector machine-based classification of Alzheimer's disease from whole-brain anatomical MRI". Neuroradiology. 51 (2): 73–83. doi:10.1007/s00234-008-0463-x. PMID 18846369. S2CID 285128.
- ^ a b N.K. Batmanghelich; B. Taskar; C. Davatzikos (2012). "Generative-discriminative basis learning for medical imaging". IEEE Trans Med Imaging. 31 (1): 51–69. doi:10.1109/TMI.2011.2162961. PMC 3402718. PMID 21791408.
- ^ a b Glenn Fung; Jonathan Stoeckel (2007). "SVM feature selection for classification of SPECT images of Alzheimer's disease using spatial information". Knowledge and Information Systems. 11 (2): 243–258. CiteSeerX 10.1.1.62.6245. doi:10.1007/s10115-006-0043-5. S2CID 9901011.
- ^ a b R. Chaves; J. Ramírez; J.M. Górriz; M. López; D. Salas-Gonzalez; I. Álvarez; F. Segovia (2009). "SVM-based computer-aided diagnosis of the Alzheimer's disease using t-test NMSE feature selection with feature correlation weighting". Neuroscience Letters. 461 (3): 293–297. doi:10.1016/j.neulet.2009.06.052. PMID 19549559. S2CID 9981775.
- ^ a b Yanxi Liu; Leonid Teverovskiy; Owen Carmichael; Ron Kikinis; Martha Shenton; Cameron S. Carter; V. Andrew Stenger; Simon Davis; Howard Aizenstein; James T. Becker (2004). "discriminative mr image feature analysis for automatic schizophrenia and alzheimer's disease classification" (PDF). Medical Image Computing and Computer-assisted Intervention – Miccai. Lecture Notes in Computer Science. 3216: 393–401. doi:10.1007/978-3-540-30135-6_48. ISBN 978-3-540-22976-6.
- ^ Savio A.; Graña M. (2013). "Deformation based feature selection for Computer Aided Diagnosis of Alzheimer's Disease". Expert Systems with Applications. 40 (5): 1619–1628. doi:10.1016/j.eswa.2012.09.009. ISSN 0957-4174.
- ^ R. Filipovych; S. M. Resnick; C. Davatzikos (2011). "Semi-supervised cluster analysis of imaging data". NeuroImage. 54 (3): 2185–2197. doi:10.1016/j.neuroimage.2010.09.074. PMC 3008313. PMID 20933091.
- ^ STEP 조사 로드맵 웨이백 머신에서 2008-08-28 아카이브 완료.europhysiome.org
- ^ J. W. Fenner; B. Brook; G. Clapworthy; P. V. Coveney; V. Feipel; H. Gregersen; D. R. Hose; P. Kohl; P. Lawford; K. M. McCormack; D. Pinney; S. R. Thomas; S. Van Sint Jan; S. Waters; M. Viceconti (2008). "The EuroPhysiome, STEP and a roadmap for the virtual physiological human" (PDF). Philosophical Transactions of the Royal Society A. 366 (1878): 2979–2999. Bibcode:2008RSPTA.366.2979F. doi:10.1098/rsta.2008.0089. PMID 18559316. S2CID 1211981.
- ^ J. B. Bassingthwaighte (2000). "Strategies for the Physiome Project". Annals of Biomedical Engineering. 28 (8): 1043–1058. doi:10.1114/1.1313771. PMC 3425440. PMID 11144666.
- ^ P. J. Hunter; T. K. Borg (2003). "Integration from proteins to organs: The Physiome Project". Nat. Rev. Mol. Cell Biol. 4 (3): 237–243. doi:10.1038/nrm1054. PMID 12612642. S2CID 25185270.
- ^ R. L.Winslow; N. Trayanova; D. Geman; M. I. Miller (2012). "Computational medicine: Translating models to clinical care". Sci. Trans. Med. 4 (158): 158rv11. doi:10.1126/scitranslmed.3003528. PMC 3618897. PMID 23115356.
- ^ N. 아야체, J.-P.Boissel, S. Brunak, G. Clapworthy, G. Lonsdale, J. Finggberg, A. F. F. Frangi, G.데코, P. J. 헌터, P.닐슨, M.Halstead, D. R. Hose, I. Magnin, F. Martin-Sanchez, P. Sloot, J. Kaandorp, A.Hoekstra, S. Van Sint Jan, M.Viceconti (2005) "가상 생리학적 인간 지향: 인체 해부학과 생리의 다단계 모델링 및 시뮬레이션"총무국 INFSO 및 총무국 JRC, 백서
- ^ Boulfelfel D.; Rangayyan R.M.; Hahn L.J.; Kloiber R.; Kuduvalli G.R. (1994). "Restoration of single photon emission computed tomography images by the Kalman filter". IEEE Transactions on Medical Imaging. 13 (1): 102–109. doi:10.1109/42.276148. PMID 18218487.
- ^ Angenent, S.; Pichon, E.; Tannenbaum, A. (2006). "Mathematical methods in medical image processing". Bulletin of the AMS. 43 (3): 365–396. doi:10.1090/S0273-0979-06-01104-9. PMC 3640423. PMID 23645963.
- ^ P Basser; J Mattiello; D LeBihan (January 1994). "MR diffusion tensor spectroscopy, imaging". Biophysical Journal. 66 (1): 259–267. Bibcode:1994BpJ....66..259B. doi:10.1016/S0006-3495(94)80775-1. PMC 1275686. PMID 8130344.
- ^ P Fillard; X Pennec; V Arsigny; N Ayache (2007). "Clinical DT-MRI estimation, smoothing,, fiber tracking with log-Euclidean metrics". IEEE Transactions on Medical Imaging. 26 (11): 1472–1482. CiteSeerX 10.1.1.218.6380. doi:10.1109/TMI.2007.899173. PMID 18041263.
- ^ S-K Song; S-W Sun; M Ramsbottom; C Cheng; J Russell; A Cross (November 2002). "Dysmyelination Revealed through MRI as Increased Radial (but Unchanged Axial) Diffusion of Water". NeuroImage. 13 (3): 1429–1436. doi:10.1006/nimg.2002.1267. PMID 12414282. S2CID 43229972.
- ^ P Barzo; A Marmarou; P Fatouros; K Hayasaki; F Corwin (December 1997). "Contribution of vasogenic and cellular edema to traumatic brain swelling measured by diffusion-weighted imaging". Journal of Neurosurgery. 87 (6): 900–907. doi:10.3171/jns.1997.87.6.0900. PMID 9384402.
- ^ D Alexander; C Pierpaoli; P Basser (January 2001). "Spatial transformation of diffusion tensor magnetic resonance images" (PDF). IEEE Transactions on Medical Imaging. 20 (11): 1131–1139. doi:10.1109/42.963816. PMID 11700739. S2CID 6559551.
- ^ Y Cao; M Miller; S Mori; R Winslow; L Younes (June 2006). "Diffeomorphic Matching of Diffusion Tensor Images". Proceedings of IEEE Computer Society Conference on Computer Vision, Pattern Recognition (CVPR), Workshop on Mathematical Methods in Biomedical Image Analysis (MMBIA 2006). New York. p. 67. doi:10.1109/CVPRW.2006.65. PMC 2920614.
- ^ Z Wang; B Vemuri (October 2005). "DTI segmentation using an information theoretic tensor dissimilarity measure". IEEE Transactions on Medical Imaging. 24 (10): 1267–1277. CiteSeerX 10.1.1.464.9059. doi:10.1109/TMI.2005.854516. PMID 16229414. S2CID 32724414.
- ^ Melonakos, J.; Pichon, E.; Angenent, S.; Tannenbaum, A. (2008). "Finsler active contours". IEEE Trans. PAMI. 30 (3): 412–423. doi:10.1109/TPAMI.2007.70713. PMC 2796633. PMID 18195436.
- ^ S Mori; B Crain; V Chacko; P van Zijl (February 1999). "Three-dimensional tracking of axonal projections in the brain by magnetic resonance imaging". Annals of Neurology. 45 (2): 265–269. doi:10.1002/1531-8249(199902)45:2<265::AID-ANA21>3.0.CO;2-3. PMID 9989633.
- ^ D Tuch; T Reese; M Wiegell; N Makris; J Belliveau; V Wedeen (October 2002). "High angular resolution diffusion imaging reveals intravoxel white matter fiber heterogeneity". Magnetic Resonance in Medicine. 48 (4): 577–582. doi:10.1002/mrm.10268. PMID 12353272.
- ^ D Tuch (December 2004). "Q-ball imaging". Magnetic Resonance in Medicine. 52 (6): 1358–1372. doi:10.1002/mrm.20279. PMID 15562495.
- ^ V Wedeen; P Hagmann; W-Y Tseng; T Reese (December 2005). "Mapping complex tissue architecture with diffusion spectrum magnetic resonance imaging". Magnetic Resonance in Medicine. 54 (6): 1377–1386. doi:10.1002/mrm.20642. PMID 16247738.
- ^ K Jansons; D Alexander (July 2003). "Persistent angular structure: new insights from diffusion magnetic resonance imaging data". Proceedings of Information Processing in Medical Imaging (IPMI) 2003, LNCS 2732. pp. 672–683. doi:10.1007/978-3-540-45087-0_56.
- ^ J-D Tournier; F Calamante; D Gadian; A Connelly (2007). "Direct estimation of the fiber orientation density function from diffusion-weighted MRI data using spherical deconvolution". NeuroImage. 23 (3): 1176–1185. doi:10.1016/j.neuroimage.2004.07.037. PMID 15528117. S2CID 24169627.
- ^ X Geng; T Ross; W Zhan; H Gu; Y-P Chao; C-P Lin; G Christensen; N Schuff; Y Yang (July 2009). "Diffusion MRI Registration Using Orientation Distribution Functions". Proceedings of Information Processing in Medical Imaging (IPMI) 2009, LNCS 5636. Vol. 21. pp. 626–637. doi:10.1007/978-3-642-02498-6_52. PMC 3860746.
- ^ P-T Yap; Y Chen; H An; Y Yang; J Gilmore; W Lin; D Shen (2011). "SPHERE: SPherical Harmonic Elastic REgistration of HARDI data". NeuroImage. 55 (2): 545–556. doi:10.1016/j.neuroimage.2010.12.015. PMC 3035740. PMID 21147231.
- ^ P Zhang; M Niethammer; D Shen; P-T Yap (2012). "Large Deformation Diffeomorphic Registration of Diffusion-Weighted Images" (PDF). Proceedings of Medical Image Computing and Computer-Assisted Intervention (MICCAI). doi:10.1007/978-3-642-33418-4_22.
- ^ M Descoteaux; R Deriche (September 2007). "Segmentation of Q-Ball Images Using Statistical Surface Evolution". Proceedings of Medical Image Computing and Computer-Assisted Intervention (MICCAI) 2007, LNCS 4792. pp. 769–776. doi:10.1007/978-3-540-75759-7_93.
- ^ a b Friston, K.; Holmes, A.; Worsley, K.; Poline, J.; Frith, C.; Frackowiak, R.; et al. (1995). "Statistical parametric maps in functional imaging: a general linear approach". Hum Brain Mapp. 2 (4): 189–210. doi:10.1002/hbm.460020402. S2CID 9898609.
- ^ Buckner, R. L.; Andrews-Hanna, J. R.; Schacter, D. L. (2008). "The brain's default network: anatomy, function, and relevance to disease". Annals of the New York Academy of Sciences. 1124 (1): 1–38. Bibcode:2008NYASA1124....1B. CiteSeerX 10.1.1.689.6903. doi:10.1196/annals.1440.011. PMID 18400922. S2CID 3167595.
- ^ a b Yeo, B. T. T.; Krienen, F. M.; Sepulcre, J.; Sabuncu, M. R.; Lashkari, D.; Hollinshead, M.; Roffman, J. L.; Smoller, J. W.; Zöllei, L.; Polimeni, J. R.; Fischl, B.; Liu, H.; Buckner, R. L. (2011). "The organization of the human cerebral cortex estimated by intrinsic functional connectivity". J Neurophysiol. 106 (3): 1125–65. doi:10.1152/jn.00338.2011. PMC 3174820. PMID 21653723.
- ^ J. V. Haxby; M. I. Gobbini; M. L. Furey; A. Ishai; J. L. Schouten; P. Pietrini (2001). "Distributed and overlapping representations of faces and objects in ventral temporal cortex". Science. 293 (5539): 2425–30. Bibcode:2001Sci...293.2425H. CiteSeerX 10.1.1.381.2660. doi:10.1126/science.1063736. PMID 11577229. S2CID 6403660.
- ^ Langs, G.; Menze, B. H.; Lashkari, D.; Golland, P. (2011). "Detecting stable distributed patterns of brain activation using Gini contrast". NeuroImage. 56 (2): 497–507. doi:10.1016/j.neuroimage.2010.07.074. PMC 3960973. PMID 20709176.
- ^ Varoquaux, G.; Gramfort, A.; Pedregosa, F.; Michel, V.; Thirion, B. (2011). "Multi-subject dictionary learning to segment an atlas of brain spontaneous activity". Inf Process Med Imaging. Vol. 22. pp. 562–73.
- ^ van den Heuvel, M. P.; Stam, C. J.; Kahn, R. S.; Hulshoff Pol, H. E. (2009). "Efficiency of functional brain networks and intellectual performance". J Neurosci. 29 (23): 7619–24. doi:10.1523/JNEUROSCI.1443-09.2009. PMC 6665421. PMID 19515930.
- ^ Friston, K. (2003). "Dynamic causal modelling". NeuroImage. 19 (4): 1273–1302. doi:10.1016/S1053-8119(03)00202-7. PMID 12948688. S2CID 2176588.
- ^ Sabuncu, M. R.; Singer, B. D.; Conroy, B.; Bryan, R. E.; Ramadge, P. J.; Haxby, J. V. (2010). "Function-based Intersubject Alignment of Human Cortical Anatomy". Cerebral Cortex. 20 (1): 130–140. doi:10.1093/cercor/bhp085. PMC 2792192. PMID 19420007.
- ^ Langs, G.; Lashkari, D.; Sweet, A.; Tie, Y.; Rigolo, L.; Golby, A. J.; Golland, P. (2011). "Learning an atlas of a cognitive process in its functional geometry". Inf Process Med Imaging. Vol. 22. pp. 135–46.
- ^ Haxby, J. V.; Guntupalli, J. S.; Connolly, A. C.; Halchenko, Y. O.; Conroy, B. R.; Gobbini, M. I.; Hanke, M.; Ramadge, P. J. (2011). "A common, high-dimensional model of the representational space in human ventral temporal cortex". Neuron. 72 (2): 404–416. doi:10.1016/j.neuron.2011.08.026. PMC 3201764. PMID 22017997.
- ^ Wells, William M; Colchester, Alan; Delp, Scott (1998). Lecture Notes in Computer Science (Submitted manuscript). Lecture Notes in Computer Science. Vol. 1496. doi:10.1007/BFb0056181. ISBN 978-3-540-65136-9. S2CID 31031333.
- ^ JS Duncan; N Ayache (2000). "Medical image analysis: Progress over two decades and the challenges ahead". IEEE Transactions on Pattern Analysis and Machine Intelligence. 22: 85–106. CiteSeerX 10.1.1.410.8744. doi:10.1109/34.824822.
의료 이미지 컴퓨팅에 관한 저널
- Medical Image Analysis(MedIA; Medical Image Analysis), MICCAI Society의 공식 저널이기도 합니다.MICCAI 연례회의는 의료 이미지 컴퓨팅을 위한 프리미어 컨퍼런스를 개최합니다.
- IEEE TMI(의료 영상 처리)
- 의학물리학
- JDI(Journal of Digital Imaging(JDI; 디지털 이미징 저널)
- 의료용 화상 처리 및 그래픽스
- 컴퓨터 지원 방사선 및 외과 저널
- BMC 의료 이미징
또한 다음 저널은 의료 이미지 컴퓨팅 또는 의료 이미지 컴퓨팅의 방법과 특정 임상 응용 분야를 설명하는 기사를 가끔 게재합니다.