스도쿠의 수학

이 문서는 자체 발행 출처에 대한 과도하거나 부적절한 참조를 포함할 수 있다. 부적절하게 사용되는 신뢰할 수 없는 소스에 대한 참조를 제거하여 개선하십시오.(2021년 9월) (이 템플릿 메시지를 제거하는 방법 및 시기 학습)

스도쿠 퍼즐은 '충분한 스도쿠 그리드가 몇 개인가', '유효한 퍼즐에 있는 최소한의 단서 수는 얼마인가', '어떤 면에서 스도쿠 그리드가 대칭적일 수 있는가' 등의 질문에 수학적으로 답할 수 있다.

주요 결과는 고전적인 스도쿠의 경우 충전된 그리드의 수가 6,670,903,752,021,072,936,960(6.67×10²¹)이며, 변환을 보존하는 유효성에 따라 본질적으로 다른 그룹 5,472,730,538로 감소한다.대칭의 종류는 26가지가 있지만, 전체 충전 그리드의 약 0.005%에서만 찾을 수 있다.독특한 해결책을 가진 퍼즐은 적어도 17개의 단서를 가지고 있어야 하며, 풀린 격자마다 최대 21개의 단서를 가진 해결 가능한 퍼즐이 있다.지금까지 발견된 가장 큰 미니멀 퍼즐에는 40개의 단서가 있다.

유사한 결과가 변형 및 소형 그리드에 대해 알려져 있다.전통적인 9×9 격자보다 큰 수도쿠스에 대해서는 정확한 결과가 알려져 있지 않지만, 상당히 정확하다고 여겨지는 추정치는 있다.

개요

스도쿠에 대한 분석은 크게 두 가지로 나뉜다.

1. 완료된 그리드의 속성 분석
2. 완료된 퍼즐의 속성 분석.

초기 분석은 주로 해결 방법을 열거하는 데 초점이 맞춰져 있었으며, 2004년에 결과가 처음 나타났다.^[1]

부분적으로는 크기(N)로 특징지어지는 스도쿠 변종이 많고, 그 지역의 형태도 다양하다.언급되지 않는 한, 이 기사의 논의는 고전적인 스도쿠(Sudoku)를 전제로 한다.N=9(9×9 격자 및 3×3 지역).직사각형 스도쿠는 열-기둥 치수 R×C의 직사각형 영역을 사용한다.다른 변형으로는 불규칙한 형태를 띠거나 추가적인 제약조건(하이퍼큐브) 또는 다른 제약조건 유형(Samunamupure)이 있다.

지역은 블록이나 상자라고도 불린다.밴드는 3열과 3박스를 캡슐화하는 그리드의 일부분이고, 스택은 3열과 3박스를 캡슐화하는 그리드의 일부분이다.퍼즐은 부분적으로 완성된 격자이며, 초기 값은 기븐이나 단서들이다.적절한 퍼즐은 독특한 해결책을 가지고 있다.최소한의 퍼즐은 추가적인 해결책을 제시하지 않고는 어떤 단서도 제거할 수 없는 적절한 퍼즐이다.다른 용어는 스도쿠 용어집을 참조하십시오.^[2]

선수 입장에서 수도쿠스를 해결하는 것은 '숨겨진 Xy-chains' 등의 전략을 고민하는 데니스 베르티에 감독의 책 '수도쿠의 숨겨진 논리'(2007)에서 탐구됐다.^[3]

수학적 맥락

n×n 블록의 n²×n² 그리드에 대한 스도쿠 퍼즐을 푸는 일반적인 문제는 NP-완전한 것으로 알려져 있다.^[4]그러나 n=3(일반적인 스도쿠)의 경우, 이 결과는 실용성이 거의 없다: 알고리즘은 문제의 크기가 작기 때문에 퍼즐을 단 1초 만에 풀 수 있다.^[5]

퍼즐은 그래프 색칠 문제로 표현될 수 있다.^[6]목적은 부분적인 9-색상이 주어진 특정 그래프의 9-색상을 구성하는 것이다.스도쿠 그래프는 각 셀마다 하나의 꼭지점인 81개의 정점을 가지고 있다.정점에는 순서가 지정된 쌍(x, y)이 표시되며 여기서 x와 y는 1과 9 사이의 정수다.이 경우 (x, y) 및 (x, y)로 표시된 두 개의 뚜렷한 정점은 다음과 같은 경우에만 에지로 결합된다.

• x = x′(수직 열) 또는,
• y = y′(수직 행) 또는,
• ⌈ x/3 ⌉ = ⌈ x′/3 ⌉, ⌈ y/3 ⌉ = ⌈ y′/3 ⌉ (same 3×3 셀)

그런 다음 가장자리로 연결된 정점이 동일한 정수를 할당하지 않는 방식으로 퍼즐은 각 정점에 1과 9 사이의 정수를 할당하여 완성된다.

스도쿠 솔루션 격자도 라틴어 사각형이다.^[6]스도쿠는 추가적인 지역적 제약을 부과하기 때문에 라틴 광장보다 스도쿠 그리드가 현저히 적다.

그룹 테이블의 수도쿠스

라틴어 사각형의 경우처럼 유한 그룹의 (추가 또는) 곱셈표(Cayley tables)를 사용하여 수도쿠스 및 관련 숫자 표를 구성할 수 있다.즉, 하위그룹과 지수를 고려해야 한다.

Take for example ${\displaystyle \mathbb {Z} _{n}\oplus \mathbb {Z} _{n}}$ the group of pairs, adding each component separately modulo some ${\displaystyle n}$. By omitting one of the components, we suddenly find ourselves in ${\displaystyle \mathbb {Z} _{n}}$ (and this mapping is obviously compat각각의 추가, 즉 집단 동형상이다.)한 사람은 또한 후자가 전자의 지수를 나타내는 그룹이라고 말하는데, 왜냐하면 한때는 다른 요소들이 새로운 그룹에서 동등해지기 때문이다.${\displaystyle {}_{}}$ Z n${\displaystyle {}_{}}$component ${\displaystyle {\mathbb{}}_{}}$ ${\displaystyle {}_{}}$ ${\$$displaystyle 0}$을(를) 단순히 $0{\displaystyle \mathrm{}}$ {\$displaystyle \mathb {Z} _{n}\oplus \mathb {Z}$$_{n}}$로 되돌리기 위해$$ 누락된 구성 요소를 단순히 0$${\displaystylement 0}으로 채울 수 있기 때문에 하위 그룹이기도 하다.

이 보기에서는 $n{\displaystyle }$= ${\displaystyle 3}$ ${\displaystyle n=3}$에 대한 그리드 1의 예를 기록하십시오$.$

각 스도쿠 지역은 첫 번째 성분과 상관없이 추가되기 때문에 두 번째 성분(이름 그대로 하위그룹 ${\displaystyle {\mathrm{}}_{}}$ 3 ${\$에서 동일하게 보인다.$$한편, 각 블록에서 첫 번째 구성요소는 동일하며, 각 블록을 하나의 셀로 상상하면, 이러한 첫 번째 구성요소는 동일한 패턴을 보인다(명칭 인용 그룹 $Z{\displaystyle {\mathbb{}}_{}}$ ${\displaystyle {\mathrm{}}_{}}$ ${\$라틴 사각형의 글에서 요약한 바와 같이, 이것은 순서 $[\displaystyle 9}$의 라틴 사각형이다$.$

자, 이제 스도쿠를 산출하기 위해서, 그런 식으로 행(또는 동등하게 기둥)을 허용하면, 각 블록을 정확히 한 번 각 블록으로 재분배할 수 있다. 예를 들어, $1{\displaystyle \mathrm{}}$,${\displaystyle }$4,${\displaystyle 7}$,${\displaystyle 2}$,${\displaystyle 5}$,${\displaystyle }$8, ${\displaystyle 3}$, ${\displaystyle 6}$, 9 $displaystyle$ 1,$4,7,$2,5$,8,3,6$,$}$을 주문하면 된다$.$ 물론 이것은 라틴 제곱 특성을 보존한다.또한 블록의 두 번째 구성요소가 원래 순서 $3$의 라틴 사각형$($부분군 ${\displaystyle {\mathrm{}}_{}}$ 3 ${\$을 형성했기 때문에 각 블록에서 선들은 시공에 의해 구별되는 첫 번째 구성요소를 가지고 있고 블록의 각 선들은 두 번째 구성요소를 통해 구별되는 항목을 가지고 있다.그래서 우리는 스도쿠에 도착한다. (원하면 쌍을 숫자 1...9로 바꿔라.)위의 예와 행 순열로 우리는 격자 2에 도착한다.

그리드 ${\displaystyle {\mathrm{}}_{}}$ – $Z{\displaystyle {\mathbb{}}_{}}$ 3 ${\displaystyle {}_{}}$ ${\displaystyle {\mathbb{}}_{}}$ ${\displaystyle {\mathrm{}}_{}}$ ${\$의 추가 표 (0,0) (0,1) (0,2) (0,1) (0,2) (0,0) (0,2) (0,0) (0,1) (1,0) (1,1) (1,2) (1,1) (1,2) (1,0) (1,2) (1,0) (1,1) (2,0) (2,1) (2,2) (2,1) (2,2) (2,0) (2,2) (2,0) (2,1) (1,0) (1,1) (1,2) (1,1) (1,2) (1,0) (1,2) (1,0) (1,1) (2,0) (2,1) (2,2) (2,1) (2,2) (2,0) (2,2) (2,0) (2,1) (0,0) (0,1) (0,2) (0,1) (0,2) (0,0) (0,2) (0,0) (0,1) (2,0) (2,1) (2,2) (2,1) (2,2) (2,0) (2,2) (2,0) (2,1) (0,0) (0,1) (0,2) (0,1) (0,2) (0,0) (0,2) (0,0) (0,1) (1,0) (1,1) (1,2) (1,1) (1,2) (1,0) (1,2) (1,0) (1,1)

그리드 2 – 스도쿠 생성 (0,0) (0,1) (0,2) (1,0) (1,1) (1,2) (2,0) (2,1) (2,2) (1,0) (1,1) (1,2) (2,0) (2,1) (2,2) (0,0) (0,1) (0,2) (2,0) (2,1) (2,2) (0,0) (0,1) (0,2) (1,0) (1,1) (1,2) (0,1) (0,2) (0,0) (1,1) (1,2) (1,0) (2,1) (2,2) (2,0) (1,1) (1,2) (1,0) (2,1) (2,2) (2,0) (0,1) (0,2) (0,0) (2,1) (2,2) (2,0) (0,1) (0,2) (0,0) (1,1) (1,2) (1,0) (0,2) (0,0) (0,1) (1,2) (1,0) (1,1) (2,2) (2,0) (2,1) (1,2) (1,0) (1,1) (2,2) (2,0) (2,1) (0,2) (0,0) (0,1) (2,2) (2,0) (2,1) (0,2) (0,0) (0,1) (1,2) (1,0) (1,1)

이 방법이 효과가 있으려면 일반적으로 크기가 같은 두 그룹의 제품이 필요하지 않다.소위 적절한 크기의 유한집단의 짧은 정확한 순서가 이미 그 일을 하고 있다.$예$를 들어, ${\displaystyle {\mathrm{}}_{}}$4 {\$displaystyle \mathb {$Z$} _${4$}$ 그룹의$$ 경우, 지수 및 부분군 ${\displaystyle {\mathrm{}}_{}}$ $2{\displaystyle {\mathbb{}}_{}}$ ${\$ (열람 인수에서 이미) 모든 Sudokus가 이러한 방식으로 생성될 수 없다는 것이 분명해 보인다.

변형

스도쿠는 폴리오미노(스도쿠 지방의 지역)가 있는 라틴어 광장의 타일링(또는 커버)으로 해석할 수 있다.고전적인 9×9 스도쿠는 네모난 노노미노로 만들어졌다.N²×N² 스도쿠 퍼즐만 사각 폴리오미노로 타일링할 수 있지만 다른 크기의 퍼즐에는 스도쿠의 규칙을 적용하는 것이 가능하다.

확장된 변형 목록은 스도쿠 용어집을 참조하십시오.

직사각형 영역

인기 있는 변종은 직사각형 영역(블록 또는 상자)으로 만들어진다. 예를 들어 6×6 격자로 타일 처리된 2×3 헥소미노가 있다.이 변형에 대해 논할 때는 다음과 같은 표기법을 사용한다.

• R×C는 R 행과 C 열을 가진 직사각형 영역을 의미한다.
• 암시적 그리드 구성의 특징은 다음과 같다.
  • 그리드 치수 N×N, 여기서 N = R×C
  • C×R '슈퍼그리드'로 배열된 R×C 크기의 블록(박스) N개
  • R×N 크기의 C 밴드, 수평으로 인접한 블록 R로 구성됨
  • 수직으로 인접한 C 블록으로 구성된 N×C 크기의 R 스택

사각형 N×N 영역을 가진 스도쿠는 각 행과 기둥이 N 영역을 교차하고 N 셀을 서로 공유하기 때문에 사각형 스도쿠보다 대칭적이다.밴드 및 스택의 수도 N과 같다."3×3" 스도쿠는 추가로 고유하다: N은 원 룰(즉, N=3유형의 단위가 있다)에 따른 행-기둥-지역 제약의 수이기도 하다.

조각수도쿠스

지역이 (필요하게) 사각형이나 직사각형이 아닌 수도쿠는 지소 스도쿠라고 알려져 있다.특히 N이 프라임인 N×N 광장은 불규칙한 N-mino로만 타일링할 수 있다.N의 작은 값에 대해 정사각형(대칭 제외)을 타일로 배열하는 방법의 수가 계산되었다(OEIS의 순서 A172477).^[7]N ≥ 4의 경우 이러한 기울기 중 일부는 라틴어 사각형과 호환되지 않는다. 즉, 그러한 타일링의 모든 스도쿠 퍼즐은 해결책이 없다.^[7]

해결 방법

'몇 개의 스도쿠 그리드가 있는가?'라는 물음에 대한 답은 유사한 해결책이 언제 다른 것으로 간주되는가에 대한 정의에 달려 있다.

일반 스도쿠

모든 솔루션

가능한 모든 해결책의 열거에 있어, 해당 (81) 셀 값 중 하나가 다른 경우 두 해결책은 구별되는 것으로 간주된다.유사한 솔루션 간의 대칭 관계는 무시된다. 예를 들어, 용액의 회전은 구별되는 것으로 간주된다.대칭은 열거 전략에서 중요한 역할을 하지만 가능한 모든 해결책의 개수에서는 그렇지 않다.

완전한 조사를 위한 최초의 알려진 해결책은 QSCGZ(Guenter Stertenbrink)가 2003년에 rec.puzles 뉴스그룹에 게시하여 6,670,903,752,021,072,936,960 (6.67×10²¹)의 구별되는 솔루션을 획득했다.^[8][9][10]

2005년 연구에서 펠젠하우어와 자비스는^[11][10] 유효한 해결책에 사용되는 최상위 밴드의 순열을 분석했다.부분 그리드 솔루션에 대한 Band1 대칭 및 동등성 등급이 식별되면, 하위 두 대역의 보완을 구성하고 각 동등성 등급에 대해 계산했다.등가 등급에 대한 보완을 클래스 크기에 따라 가중하여 합산하면 총 솔루션 수가 6,670,903,752,021,072,936,960으로 나타나 QSCGZ가 획득한 값을 확인할 수 있다.그 가치는 그 후에 독립적으로 수없이 확인되었다.후에 밴드 생성을 기반으로 한 두 번째 열거 기법이 개발되었는데, 이는 계산적으로 상당히 덜 집약적이다.이 후속 기법은 원래 기법으로 계산 주기 수의 97분의 1을 대략 필요로 하였으나, 설정하기가 훨씬 더 복잡했다.

본질적으로 다른 솔루션

변환을 보존하는 유효성

두 개의 유효 그리드는 이른바 VPT(Validity reserving transformation)를 사용하여 다른 하나로부터 파생될 수 있다면 본질적으로 동일하다.이러한 변환은 항상 유효한 그리드를 다른 유효한 그리드로 변환한다.크게 두 가지 유형이 있는데, 기호 순열(릴라벨링)과 셀 순열(재범위)이다.다음 구성 요소:

• 기호 다시 라벨링(9!)
  (예를 들어 상단 행을 [123456789]로 고정시키는 것을 제외하고 가능한 모든 재형성 조합이 제거되면 고정 그리드의 수는 18,383,222,420,692,992로 감소한다.이 값은 6,670,903,752,021,072,936,960을 9로 나눈 값!)

및 재배열(흔들림):

• 밴드 순열(3!)
• 밴드 내 행 순열(3!×3!×3!)
• 순열 쌓기(3!)
• 스택 내의 열 순열(3!×3!×3!)
• 반사, 전위 및 회전(2)
  (위의 순열과 연계하여 단일 전이 또는 1/4회전 회전을 할 경우 반사, 전이, 회전의 조합이 생성될 수 있으므로, 이러한 연산은 2의 요인만 기여한다.)

이러한 운영은 등가 그리드 간의 관계를 정의한다.81개의 그리드 셀 값에 관하여, 재배열 연산은 대칭₈₁ 그룹 S의 하위 그룹을 형성한다. 순서 3!×⁸2 = 3,359,232.다시 샘플링 작업은 S와₉ 이형성이며 9! = 362,880 등가 그리드를 추가로 생성한다.그리드에 이러한 작업을 적용하면 3!×⁸2×9! 또는 1,218,998,108,160 본질적으로 동등한 그리드가 된다.그러나 위의 작업에서 그리드가 더 적게 발생하는 소수의 수도쿠스(sudokus)가 있다. 이는 자기 유사성 또는 자동형 수도쿠스(automorphic sudokus)이다.모든 본질적으로 고유한 그리드의 약 0.01%만이 자동형이지만,^[12] 그것들을 세는 것은 본질적으로 다른 수도의 정확한 수를 평가하기 위해 필요하다.

스도쿠 대칭군

스도쿠 대칭군의 정밀한 구조는 화환제품(花 wreath제품)을 사용하여 간결하게 표현할 수 있다.가능한 행(또는 열) 순열은 순서 3!⁴ = 1,296의 S에₃₃ 대한 이형 집단을 형성한다.^[13]전체 재배열 그룹은 그 그룹의 2개의 복사본에 대해 한 개는₂ 행 순열, 한 개는 열 순열로, 한 개는 열 순열로, 한 개는 해당 그룹의 2개의 복사본에 대해 작용하도록 하여 형성된다.이것은 순서 1,296₃ × 2 = 3,359²,232의 그룹인 S₃ ≀ S ≀ C이다₂.마지막으로, 라벨링 운영은 재배열 운영과 함께 통근하기 때문에 전체 스도쿠(VPT) 그룹은 (S₃ s₃ S c C₂) × 순서 1,218,998,108,160의₉ S이다.

고정 포인트 및 번사이드 보조정리

이러한 작업을 사용하여 도달할 수 있는 등가 그리드 집합(다시 모델링 제외)은 재배열 그룹의 작용에 따라 그리드의 궤도를 형성한다.본질적으로 다른 해결책의 수는 그 다음 번사이드의 보조정리기를 사용하여 계산할 수 있는 궤도의 수입니다.Burnside 고정점은 재배열 작업 시 변경되지 않거나 재조립에 의해서만 달라지는 그리드다.계산을 단순화하기 위해 재배열 그룹의 요소는 모두 동일한 수의 고정점을 갖는 결합 등급으로 분류된다.재배열 집단의 275개의 결합 등급 중 27개만 고정 포인트를 가지고 있는 것으로 나타났다;^[14] 이러한 결합 등급은 완성된 수도쿠 그리드에서 찾을 수 있는 다른 형태의 대칭(자기 유사성 또는 자동성)을 나타낸다.이 기법을 사용하여, 에드 러셀과 프레이저 자비스는 본질적으로 다른 스도쿠 솔루션의 수를 5,472,730,538로 계산한 최초의 사람이었다.^[14][15]

고정점("자동화" 및 그 유병률)^[14]을 갖는 재배열 집단의 결합 등급

이름 또는 구성[16]	코드	클래스 id.[14]	클래스 사이즈를[14] 맞추다	셀 주기	O [16]	F [16]	고정 격자 수 (다시 샘플링할 때까지), 원소당[14]	고정 그리드 수, 원소당	고정 격자 수 (다시 샘플링할 때까지), 학급 전체	고정 격자 수 학급 전체
아이덴티티	e	1	1		1	81	18,383,222,420,692,992	6,670,903,752,021,072,936,960	18,383,222,420,692,992	6,670,903,752,021,072,936,960
미니 행(MR)	ccc	8	16	27×3	3	0	107,495,424	39,007,939,461,120	1,719,926,784	624,127,031,377,920
2 MR, 1 MD	ccc c	7	96	27×3	3	0	21,233,664	7,705,271,992,320	2,038,431,744	739,706,111,262,720
1 MR, 2 MD	ccccc cc	9	192	27×3	3	0	4,204,224	1,525,628,805,120	807,211,008	292,920,730,583,040
미니 대각선(MD)	ccc ccc	10	64	27×3	3	0	2,508,084	910,133,521,920	160,517,376	58,248,545,402,880
점프 행(JR)	C	25	144	27×3	3	0	14,837,760	5,384,326,348,800	2,136,637,440	775,342,994,227,200
2 JR, 1 GR	C	28	864	27×3	3	0	2,085,120	756,648,345,600	1,801,543,680	653,744,170,598,400
1 JR, 2 GR	C cc	30	1,728	27×3	3	0	294,912	107,017,666,560	509,607,936	184,926,527,815,680
글라이딩 행(GR)	Ccc	32	1,152	27×3	3	0	6,342,480	2,301,559,142,400	7,306,536,960	2,651,396,132,044,800
전체 행(FR)	C9	27	288	9×9	9	0	5,184	1,881,169,920	1,492,992	541,776,936,960
2 FR, 1 WR	C9 c	26	1,728	9×9	9	0	2,592	940,584,960	4,478,976	1,625,330,810,880
1 FR, 2 WR	C9 cc	29	3,456	9×9	9	0	1,296	470,292,480	4,478,976	1,625,330,810,880
행 흔들기(WR)	C9 ccc	31	2,304	9×9	9	0	648	235,146,240	1,492,992	541,776,936,960
점프 대각선(JD)	CC	22	5,184	27×3	3	0	323,928	117,546,992,640	1,679,242,752	609,363,609,845,760
부러진 열(BC)	C C9	24	20,736	9×9	9	0	288	104,509,440	5,971,968	2,167,107,747,840
전체 대각선(FD)	C9 C9	23	20,736	9×9	9	0	162	58,786,560	3,359,232	1,218,998,108,160
대각선 미러(DM)	T	37	1,296	36×2	2	9	30,258,432	10,980,179,804,160	39,214,927,872	14,230,313,026,191,360
DM+MD	T ccc	40	10,368	3×3, 12×6	6	0	1,854	672,779,520	19,222,272	6,975,378,063,360
DM+JD	TC	43	93,312	3×3, 12×6	6	0	288	104,509,440	26,873,856	9,751,984,865,280
쿼터 턴(QT)	TS	86	69,984	20×4	4	1	13,056	4,737,761,280	913,711,104	331,567,485,419,520
하프 턴(HT)	드링크.	79	2,916	40×2	2	1	155,492,352	56,425,064,693,760	453,415,698,432	164,535,488,647,004,160
기둥 스틱(CS)	드링크.	134	972	36×2	2	9	449,445,888	163,094,923,837,440	436,861,403,136	158,528,265,969,991,680
CS+MC	cS6 sss	135	3,888	3×3, 12×6	6	0	27,648	10,032,906,240	107,495,424	39,007,939,461,120
CS+GR	cS6 C6	142	31,104	3×3, 12×6	6	0	6,480	2,351,462,400	201,553,920	73,139,886,489,600
CS+ JR/B2, GR/B13	S6 C6	143	15,552	3×3, 12×6	6	0	1,728	627,056,640	26,873,856	9,751,984,865,280
CS+ GR/밴드2,JR/B13	cs C6	144	15,552	3×3, 12×6	6	0	3,456	1,254,113,280	53,747,712	19,503,969,730,560
CS+JR	S C6	145	7,776	3×3, 12×6	6	0	13,824	5,016,453,120	107,495,424	39,007,939,461,120
(비필수)									949,129,933,824	344,420,270,386,053,120
총계									18,384,171,550,626,816	6,671,248,172,291,458,990,080

그리드는 동시에 여러 변환의 고정점일 수 있다는 점에 유의하십시오. 예를 들어 1/4회전 대칭이 있는 그리드는 절반 회전 대칭도 가진다.특정 그리드를 고정하는 모든 변환의 조합은 해당 그리드의 스태빌라이저 부분군("자동형성 그룹")이다.

스태빌라이저 부분군

러셀은 예시 그리드, 그룹 내 VPT 결합 클래스, 발전기 세트 및 해당 스태빌라이저 클래스와 본질적으로 다른 그리드(궤도)의 수와 함께 122개의 "본질적으로 다른" 비 안정화 부분군 결합 클래스("자율주의 그룹")^[17][18] 목록을 작성했다.이형성까지 26개의 다른 집단 구조가 있다.^[19]다음 섹션에 나열된 15개의 가능한 스태빌라이저 그룹 크기가 있다.

본질적으로 동등한 그리드 수

본질적으로 고유한 각 그리드는 본질적으로 동등한 그리드의 수에서 '결함'을 평가하기 위해 자기 유사성("자율성")에 대해^[12] 분석할 수 있다.그 결과는 아래 표에 요약되어 있다.5,472,730,538개 중 총 560,151개 그리드(약 1/10,000개)는 본질적으로 고유한 그리드(비경쟁적 스태빌라이저)의 형태를 가진다.

궤도 크기(즉, 본질적으로 동등한 그리드의 수)는 궤도-안정제 정리를 이용하여 계산할 수 있다: 그것은 스도쿠 대칭 그룹의 크기를 스태빌라이저(또는 "자율형") 그룹의 크기로 나눈 것이다.궤도 크기로 본질적으로 고유한 그리드(궤도 수)의 수를 곱하면 해당 스태빌라이저 그룹 크기를 가진 그리드의 총 개수를 얻을 수 있다. 그리고 다시 한 번 합하면 가능한 스도쿠 그리드의 총 개수를 얻을 수 있다."자동형" 그리드는 궤도가 작아서 무작위 그리드의 대칭성이 떨어질 확률은 근본적으로 다른 그리드의 경우 약 10,000분의 1에서 모든 그리드의 경우 약 20,000분의 1로 떨어진다.

스태빌라이저 그룹 크기별^[12] 스도쿠 그리드 수

크기 스태빌라이저 무리를 짓다	본질적으로. 고유 격자 (궤도 수)	등가 격자 (크기 크기), 다시 샘플링 무시	그리드 수, 다시 샘플링 무시	등가 그리드(또는 비트 크기), 다시 샘플링하는 것을 포함하여	총 그리드 수
1	5,472,170,387	3,359,232	18,382,289,873,462,784	1,218,998,108,160	6,670,565,349,282,175,057,920
2	548,449	1,679,616	921,183,715,584	609,499,054,080	334,279,146,711,121,920
3	7,336	1,119,744	8,214,441,984	406,332,702,720	2,980,856,707,153,920
4	2,826	839,808	2,373,297,408	304,749,527,040	861,222,163,415,040
6	1,257	559,872	703,759,104	203,166,351,360	255,380,103,659,520
8	29	419,904	12,177,216	152,374,763,520	4,418,868,142,080
9	42	373,248	15,676,416	135,444,234,240	5,688,657,838,080
12	92	279,936	25,754,112	101,583,175,680	9,345,652,162,560
18	85	186,624	15,863,040	67,722,117,120	5,756,379,955,200
27	2	124,416	248,832	45,148,078,080	90,296,156,160
36	15	93,312	1,399,680	33,861,058,560	507,915,878,400
54	11	62,208	684,288	22,574,039,040	248,314,429,440
72	2	46,656	93,312	16,930,529,280	33,861,058,560
108	3	31,104	93,312	11,287,019,520	33,861,058,560
162	1	20,736	20,736	7,524,679,680	7,524,679,680
648	1	5,184	5,184	1,881,169,920	1,881,169,920
>1	560,151		932,547,230,208		338,402,738,897,879,040
	5,472,730,538		18,383,222,420,692,992		6,670,903,752,021,072,936,960

기타 변형

많은 스도쿠 변형에 대한 열거 결과가 계산되었다. 이것들은 아래에 요약되어 있다.

추가 제약이 있는 스도쿠

다음은 고전 3×3 스도쿠(9×9 격자)의 모든 제한 사항이다.형식 이름이 표준화되지 않음: 정의를 보려면 속성 링크를 클릭하십시오.

유형	격자수	귀인	확인하셨습니까?
준매직 스도쿠	248,832	존스, 퍼킨스, 로치[20]	네[citation needed]
매직 스도쿠	5,971,968	스테르텐브링크[21]	네[citation needed]
하이퍼큐브	37,739,520	스테르텐브링크[22]	네[citation needed]
3도쿠	104,015,259,648	스테르텐브링크[23]	네[citation needed]
NRC 수도쿠	6,337,174,388,428,800	브루워[24]	네[citation needed]
스도쿠 10세	55,613,393,399,531,520	러셀[25]	네[citation needed]
디스조인트 그룹	201,105,135,151,764,480	러셀[26]	네[citation needed]

직사각형의 지역을 가진 스도쿠

표에서 블록 치수는 지역의 치수(예: 일반 스도쿠의 3×3)이다."Rel Err" 열은 계산된 밴드 카운트에 기반한 단순^[27] 근사치(아래 절에 자세히 설명됨)가 실제 그리드 카운트와 비교하는 방법을 나타낸다. 즉, 지금까지 평가된 모든 사례에서 과소평가된 것이다.사각 블록 그리드(n² × n²)의 숫자는 (OEIS의 경우 순서 A107739), 2 × n 블록(2n × 2n 그리드)의 번호는 (OEIS의 순서 A291187)에 열거되어 있다.

라틴어 사각형과 유사하게 첫 번째 블록은 표준화된 형태의 일대일 대응성이 있으며, 이 경우 맨 위 행과 맨 왼쪽 열이 모두 정렬된다(즉, 규칙이 허용하는 한 블록 내 및 스택/밴드 자체).$R{\displaystyle }$ ${\displaystyle \times }$ ${\displaystyle C}$ ${\displaystyle R\times C}$ 블럭이$$ 있는 그리드의 경우, 각 그리드는 다음과 같다.

총 그리드(일반 ^[28][29]3×3 스도쿠의 경우 9! × 72² 또는 1,881,169,920).아래에서 논의한 변환('Sudoku 대칭')을 보존하는 전체 유효성 집합의 작용과는 달리, 이러한 감소는 항상 일대일이다.

치수		전체 그리드 수				에스트 에러 (아래 참조)	의 분수 라틴 네모
격자무늬	블록	정확한	규모	귀인	확인하셨습니까?
4×4	2×2	288	2.8800×102	여러[30] 가지	네	−11.1%	0.5×100
6×6	2×3	28,200,960	2.8201×107	페테르센[31]	네[32]	−5.88%	3.5×10−2
8×8	2×4	29,136,487,207,403,520	2.9136×1016	러셀[32]	네[33]	−1.91%	2.7×10−4
9×9	3×3	6,670,903,752,021,072,936,960	6.6709×1021	스테르텐브링크[8]	네[10]	−0.207%	1.2×10−6
10×10	2×5	1,903,816,047,972,624,930,994,913,280,000	1.9038×1030	페테르센[34]	네[35]	−0.375%	1.9×10−7
12×12	3×4	81,171,437,193,104,932,746,936,103,027,318,645,818,654,720,000	8.1171×1046	페테르센/은색[36]	아니요.	−0.132%[36]	알 수 없는
12×12	2×6	38,296,278,920,738,107,863,746,324,732,012,492,486,187,417,600,000	3.8296×1049	페테르센[37]	아니요.	−0.238%[37]	알 수 없는
15×15	3×5	알 수 없는	est. 3.5086×1084	은색[38]	아니요.	n/a	알 수 없는
16×16	4×4	알 수 없는	EST 5.954×1098	은색[39]	아니요.	n/a	알 수 없는
20×20	4×5	알 수 없는	EST 3.1764×10175	은색[40]	아니요.	n/a	알 수 없는
25×25	5×5	알 수 없는	est. 4.3648×10308	실버/페테르센[41]	아니요.	n/a	알 수 없는

해결된 스도쿠는 변환을 보존하는 유효성의 작용에 따라 유효하게 유지된다(Jarvis^[14] 참조).각 변환에 대한 불변 그리드의 수를 세어 보면 본질적으로 다른 스도쿠 그리드의 수를 계산할 수 있다(위 참조).다른 차원의 스도쿠 그리드에 유사한 방법이 적용되었다. 그 결과는 아래 표에 요약되어 있다.사각 블록 그리드(OEIS의 순서 A109741)의 경우, 전환 변환이 VPT(대칭) 그룹에 포함될 수도 있고 아닐 수도 있다(아래 참조).본질적으로 다른 그리드의 수는 (알고 있거나 추정된) 총 그리드의 수를 VPT 그룹의 크기(쉽게 계산된)로 나누어 추정할 수 있으며, 이는 기본적으로 자동형 수도쿠스의 수를 무시할 수 있다고 가정한다.2 × n 블록(2n × 2n 그리드)에 대한 번호는 (OEIS의 순서 A291188)에 열거되어 있다.

치수		VPT 그룹			본질적으로 다른 그리드 수	참조
격자무늬	블록	T	크기	콘지 클래스 (다시 라벨 표시 포함)
4×4	2×2	네	128 × 4!		2	[42][43]
		아니요.	64 × 4!		3
6×6	2×3	아니요.	3,456 × 6!	90	49	자비스/러셀,[44] 페테르센[42]
8×8	2×4	아니요.	4,423,368 × 8!	400	1,673,187	러셀,[45] 페테르센[42]
9×9	3×3	네	3,359,232 × 9!	275	5,472,730,538	자비스/러셀,[14] 페테르센[46][42]
		아니요.	1,679,616 × 9!	484	10,945,437,157
10×10	2×5	아니요.	110,592,000 × 10!	1260	4,743,933,602,050,718	페테르센/러셀[47][48]
16×16	4×4	네	(4!)10 × 2 × 16!		EST 2.2458×1071	(문자로 설명됨)[49]
		아니요.	(4!)10 × 16!		est. 4.4916×1071

추정방법

케빈 킬포일^[50](Pettersen에^[27] 의해 일반화됨)의 방법을 사용하여 가능한 완성된 대역과 스택의 수를 사용하여 완성된 그리드의 수를 추정할 수 있다.이 방법은 스도쿠 행과 열 제약조건이 박스 제약조건에 따라 조건부로 독립적이라고 주장한다.Kilfoil-Silver-Pettersen 공식:^[27]

${\displaystyle {\mbox{R}}}}\simeq {\frac {(b_{R,C})^{C}\time (b_{C,R})^{R}}}{R}}}{R}}{RC(RC)!^{R}^{{R}!^{{{{{{}}}}}}}}^{RC}}}$

어디 b수평으로(동등하게, bC, R{\displaystyle b_{C,R}}수직으로 CRC×C 스택 인접한 R×C 상자 채우는 방법 중)R의 R×RC 밴드 인접한 R×C 상자 채우고, 분모(RC)의 R, C{\displaystyle b_{R,C}}은 수이다.방법 합격. 그 그리드에 달성해야 하는 RC이다.상자만 뒤틀리는 것.

페테르센이 설명한 대로: "X는 이렇게 하자: 합법적인 수도쿠 악단이 지은 $({\displaystyle n}$ m${\displaystyle }$)${\displaystyle \times }$ (${\displaystyle n}$ m ) × (n m${\displaystyle }$) × (n ${\displaystyle m}$ ) ${\displaystyle (nm)\times (nm)}$ - grrides의$$ 공간이 되되, 칼럼이 스도쿠의 규칙을 따르는지 여부에 대해서는 전혀 관심이 없다.X의 크기는 $b{\displaystyle }$ ${\displaystyle (n^{}}$ ${\displaystyle ,}$ m${\displaystyle {}^{}}$) m ${\$ 또한 Y도 행에 주의를 기울이지 않고 합법적인 스택에 의해 구축된 그리드의 집합이 되도록 하자, #Y는 그 $다음{\displaystyle }$ b${\displaystyle }$( ${\displaystyle m}$, ${\displaystyle n{}^{}}$)${\displaystyle n^{}}$ ${\$이다$.$nxm-sudoku 그리드는 X와 Y의 교차점이다.무작위 $x{\displaystyle }$ (${\displaystyle \in }$ ${\displaystyle X}$) ${\displaystyle$ x$(\in$ X$)}$과 $y{\displaystyle }$( ${\displaystyle y}$Y${\displaystyle )}$ ${\$$displaystyle$ $y$$(\in$ $Y$$)}$은 확률$({\displaystyle n}$ ${\displaystyle m}$)이 있는 주어진 상자에서 동일하며$,$ 이러한 확률은 각 박스에 대해 독립적이라는 가정 하에 위의 추정치에 도달한다."^[27]

이 추정치는 고전적인 9×9 그리드의 경우 약 0.2%까지 정확하고, 정확한 값이 알려진 대형 그리드의 경우 1% 이내에서 정확하다는 것이 입증되었다(위 표 참조).

밴드수

R×C 크기의 블록이 있는 채운 수도쿠 그리드에서$$ b ${\displaystyle R_{}}$, C ${\$ 가능한 대역의 수에 대한 정확한 공식은 다음과 같이 알려져 있다.

치수		밴드수	귀인	확인하셨습니까?
밴드	블록
2×2C	2×C	${\displaystyle b_{2,C}=(2C)!(C!)^{2}}$	(실제 결과)	네[citation needed]
3×3C	3×C	${\displaystyle b_{3,C}=(3C)!(C!)^{6}\sum _{k=0}^{C}{C \c 선택 k}^{3}}}$ 여기서 합계가 CFranelth 번호로 알려져 있다(OEIS에서 시퀀스 A000172).	페테르센[31]	네[citation needed]
4×4C	4×C	${\displaystyle b_{4,C}=(4C)!(C!)^{12}\sum _{a,b,c}{\frac {C!^{2}}:{a!b!c!}}\cdot \sum _{k_{12},k_{13},k_{14}, \atop k_{23},k_{24},k_{34}}{{a \choose k_{12}}{b \choose k_{13}}{c \choose k_{14}}{c \choose k_{23}}{b \choose k_{24}}{a \choose k_{34}}}\right)^{2}}}$ 여기서: 외부 합계는 0≤a,b,c 및 a+b+c=2C가 되도록 모든 a,b,c를 인수한다. 내측 합계는 모든 k12,k1314,k23,k,k24,k,k34 0 0을 차지하여 다음과 같이 한다. k12,k34 ≤ a and k13,k24 ≤ b 그리고 k14,k23 ≤ c와 k12+k13+k14 = a−k12+k23+k24 = b−k13+c−k23+k34 = c−k14+b−k24+a−k34 = C 외부 합계는 각각 2박스의 두 "하위 밴드"로 밴드를 분할하는 것에 해당한다. 숫자 a, b, c는 분할을 설명하고 두 서브밴드 모두 일치해야 하므로 합계를 제곱할 수 있다. 분할 변수는 다음과 같이 설명된다: "a는 첫 번째 상자의 1행과 2행의 기호 수(즉, 상자 1의 1행과 상자 2의 2행 또는 상자 2의 1행, 상자 1의 2행 중 하나)그리고 처음 두 상자의 3행과 4행의 기호 수, 그리고 두 개의 마지막 상자의 1행과 2행의 기호 수, 처음 두 상자의 3행과 4행의 기호 수가 된다. b는 첫 번째 두 상자의 1행과 3행의 기호 수, 그리고 변수 a와 같은 다른 조합이 된다. c는 다음과 같다.처음 두 상자의 1열과 4열에 있는 기호 수입니다."[51] 내부 합계는 주어진 a,b,c 사양에 대한 서브밴드 수를 카운트한다: "상자 1과 2의 행에 있는 기호 중에서 k는12 상자 1의 1열(따라서 상자 2의 행에도 있는 기호) 중 몇 개를 카운트한다.일반적으로 i(j)의 경우 처음 두 상자의 i열과 j열 기호 중 k열은ij 1번 상자의 i열과 2번 상자의 j열 중 몇 개인지 알려준다.[51]	페테르센[52]	네[53]

아래에 몇 가지 알려진 밴드 수가 나열되어 있다.Silver에 의해 구현되고 개선된 ^[54]Petersen의 알고리즘은 밴드를 하위 밴드로 분할하고,^[55] 그 다음 동등성 등급으로 분류된다; 그것은 현재 이 b를_R,C 정확하게 평가하기 위해 알려진 가장 빠른 기법이다.

치수		밴드수	귀인	확인하셨습니까?
밴드	블록
3×6	3×2	6! × 2!6 × 10 = 460800	페테르센(공식)
3×9	3×3	9! × 3!6 × 56 = 9! × 2612736 = 948109639680 ≈ 9.4811×1011 (44개의 등가 등급[11][56])	다양한[11][31]
3×12	3×4	12! × 4!6 × 346 = 31672366418991513600 ≈ 3.1672×1019	스테르텐브링크[citation needed]	네[57]
3×15	3×5	15! × 5!6 × 2252 ≈ 8.7934×1027	페테르센(공식)[38]
(보다 큰 3×C 값은 위에 제공된 공식을 사용하여 쉽게 계산할 수 있음)
4×8	4×2	8! × 2!12 × 5016 = 828396011520 ≈ 8.2840×1011	[필요하다]
4×12	4×3	12! × 3!12 × 2180544 = 2273614462643364849254400 ≈ 2.2736×1024	페테르센[31]	네[57]
4×16	4×4	16! × 4!12 × 1273431960 ≈ 9.7304×1038	은색[39][58]	네[citation needed]
4×20	4×5	20! × 5!12 × 879491145024 ≈ 1.9078×1055	러셀[58]	네[citation needed]
4×24	4×6	24! × 6!12 × 677542845061056 ≈ 8.1589×1072	러셀[58]	네[citation needed]
4×28	4×7	28! × 7!12 × 563690747238465024 ≈ 4.6169×1091	러셀[58]	네[citation needed]
(최대 4×100까지 계산은 Silver가 수행했지만 여기에 나열되지 않음)[59]
5×10	5×2	10! × 2!20 × 364867776 ≈ 1.3883×1021 (355 동등[34] 등급)	[필요하다]	아니요.
5×15	5×3	15! × 3!20 × 324408987992064 ≈ 1.5510×1042	은색[40]	네same author, different method
5×20	5×4	20! × 4!20 × 518910423730214314176 ≈ 5.0751×1066	은색[40]	네same author, different method
5×25	5×5	25! × 5!20 × 1165037550432885119709241344 ≈ 6.9280×1093	페테르센 / 실버[41]	아니요.
5×30	5×6	30! × 6!20 × 3261734691836217181002772823310336 ≈ 1.2127×10123	페테르센 / 실버[41]	아니요.
5×35	5×7	35! × 7!20 × 10664509989209199533282539525535793414144 ≈ 1.2325×10154	페테르센 / 실버[60]	아니요.
5×40	5×8	40! × 8!20 × 39119312409010825966116046645368393936122855616 ≈ 4.1157×10186	페테르센 / 실버[55]	아니요.
5×45	5×9	45! × 9!20 × 156805448016006165940259131378329076911634037242834944 ≈ 2.9406×10220	페테르센 / 실버[citation needed]	아니요.
5×50	5×10	50! × 10!20 × 674431748701227492664421138490224315931126734765581948747776 ≈ 3.2157×10255	페테르센 / 실버[citation needed]	아니요.
6×12	6×2	12! × 2!30 × 9480675056071680 = 4876139207527966044188061990912000 ≈ 4.8761×1033	페테르센[61]	아니요.

퍼즐

최소 기븐 수

보통의 수도쿠스(속성 퍼즐)는 독특한 해결책을 가지고 있다.최소한의 스도쿠는 적당한 스도쿠를 남겨두고 어떤 실마리도 제거할 수 없는 스도쿠다.다른 최소한의 수도쿠스는 다른 수의 단서를 가질 수 있다.이 절에서는 적절한 퍼즐을 위한 최소 기븐 수를 논한다.

일반 스도쿠

17개의 단서를 가진 스도쿠.

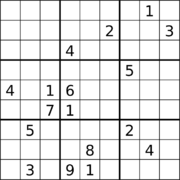
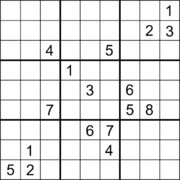17개의 단서와 대각선 대칭을 가진 스도쿠.[62]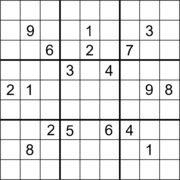

18개의 단서와 직교 대칭을 가진 스도쿠.[63]

24개의 단서와 완전한 기하학적 대칭을 가진 자동화된 스도쿠.[64]

19개의 단서와 2방향 직교 대칭을 가진 스도쿠.[65]

비록 그것들을 발견하는 것이 사소한 일은 아니지만, 많은 수도쿠스들이 17개의 단서를 가지고 발견되었다.^[66][67]게리 맥과이어, 바스티안 투게만, 길레스 시바리오의 논문은 2012년 1월 1일 발표한 논문에서 적절한 스도쿠의 최소 단서 수는 17개라는 것이 철저한 컴퓨터 검색을 통해 어떻게 증명되었는지를 설명하고 있으며,^[68][69][13] 이는 2013년 9월에 독자적으로 확인되었다.^[70]대각선 대칭이 있는 몇 개의 17-클루 퍼즐은 고든 로일의 17-클루 퍼즐 데이터베이스의 동등성 변환을 통한 검색 후에 에드 러셀에 의해 제공되었다.^[71][62]18개의 단서가 있는 스도쿠 퍼즐은 180° 회전 대칭으로, 두 경우 모두 이 숫자가 최소인지는 알 수 없지만 직교 대칭이 있는 퍼즐이 발견되었다.^[63]19개의 단서가 있는 스도쿠 퍼즐은 양방향 직교 대칭으로 발견되었고, 이 단서 수가 이 경우에 미미한지는 다시 한 번 알 수 없다.^[65]

24개의 단서인 2면 대칭(직교축의 대칭, 90° 회전 대칭, 180° 회전 대칭, 대각선 대칭)이 존재하는 것으로 알려져 있으며, 또한 자동형이다.여기서도 역시 이 정도의 단서가 이 스도쿠 계급에게 미미한 것인지는 알 수 없다.^[64][72]양방향 대각 대칭이 있는 스도쿠에서 가장 적은 단서는 18개로 생각되며, 적어도 한 경우 그러한 스도쿠도 자동성을 보인다.

본질적으로 다른 솔루션 그리드 5,472,730,538개 중에서 20개의 단서 퍼즐을 가지고 있지 않은 것은 4개뿐이며, 그 4개 그리드는 21개의 클루 퍼즐을 가지고 있다.^[73]

다른 크기의 수도쿠스

• 4×4(2×2) 스도쿠:어떤 4×4 스도쿠에서 가장 적은 단서는 4개인데, 그 중 13개의 비등가 퍼즐이 있다.(이 정도 크기의 비등가 최소 스도쿠스의 총 수는 36개)^[74]
• 6×6(2×3) 스도쿠:가장 적은 단서는 8이다.^[75]
• 8×8(2×4) 스도쿠:가장 적은 단서는 14개다.^[75]
• 10×10(2×5) 스도쿠:적어도 22개의 단서를 가진 퍼즐이 하나 만들어졌다.^[76]이것이 가능한 한 가장 적은 것인지는 알려져 있지 않다.
• 12×12(2×6) 스도쿠:적어도 32개의 단서를 가진 퍼즐이 하나 만들어졌다.^[76]이것이 가능한 한 가장 적은 것인지는 알려져 있지 않다.
• 12×12(3×4) 스도쿠:적어도 30개의 단서를 가진 퍼즐이 하나 만들어졌다.^[76]이것이 가능한 한 가장 적은 것인지는 알려져 있지 않다.
• 15×15(3×5) 스도쿠:적어도 48개의 단서를 가진 퍼즐이 하나 만들어졌다.^[76]이것이 가능한 한 가장 적은 것인지는 알려져 있지 않다.
• 16×16(4×4) 스도쿠:55개의 단서를 가진 퍼즐이 적어도 한 개 이상 만들어졌다.^[76]이것이 가능한 한 가장 적은 것인지는 알려져 있지 않다.
• 25×25(5×5) 스도쿠: 151개의 단서를 가진 퍼즐이 만들어졌다.^{[77][citation needed]}이것이 가능한 한 가장 적은 것인지는 알려져 있지 않다.

추가 제약이 있는 스도쿠

3×3 수도쿠스에 대한 추가 제약은 최소의 단서 수로 이어진다.

• 디스조인트 그룹: 글렌 파울러에 의해 12개짜리 퍼즐이^[78] 증명되었다.이후 11클루 퍼즐도 발견됐다.이것이 최선인지는 알 수 없다.
• 하이퍼큐브: 다양한 8-클루 퍼즐이^[79] Guenter Stertenbrink에 의해 입증되었다.이것이 최선이다.
• 매직 스도쿠: 구엔터 스테르텐브링크가 제공한 7클루 예시^[80].이것이 최선인지는 알 수 없다.
• 반 나이팅 스도쿠: 정확히 4개의 본질적으로 다른 8-클루 퍼즐이 존재하며 데이비드 클라미지 외 에 의해 생성되었다.^[81]이게 최선이야.
• 스도쿠 X: 552952 12클루 퍼즐^[82] 목록이 수집되었다.이것이 최선인지는 알 수 없다.
• NRC 수도쿠: 앤드리 브루워가 제공한 11-클루 예는^[24] 다음과 같다.이것이 최선인지는 알 수 없다.
• 2-Quasi-Magic Sudoku: 4-clue의^[83] 예는 토니 포브스에 의해 제공되었다.이것이 최선이라는 의심을 받고 있다.

여러 제약조건을 결합함으로써 유효한 2클루 스도쿠를 만들 수 있다.^[84]

불규칙한 지역을 가진 스도쿠

'두섬오'(^[85]지오메트리 번호판) 퍼즐은 스도쿠의 3×3(또는 R×C) 지역을 일정한 크기의 불규칙한 모양으로 대체한다.밥 해리스는 N×N 그리드에서 항상 (N - 1)클루 뒤섬오(du-sum-oh)를 만드는 것이 가능하다는^[86] 것을 증명했고, 몇 가지 예를 구성했다.요한 드 루이터는 어떤 N>3에도 N 크기의 불규칙한 모양을 가진 스도쿠 퍼즐로 바꿀 수 없는 폴리오미노 기울기가 존재한다는 것을 증명했다^[87].

합계번호위치("킬러 스도쿠")

합계 수 장소(Samunampure)에서는 어떤 행, 열 또는 지역에서도 반복 값이 없다는 통상적인 제약조건이 적용된다. 또한, 반복을 포함할 수 없는 다양한 크기와 모양의 추가 지역("카이지")이 존재하며, 그 안에 숫자의 합을 제공한다(예: 합계 10을 가진 4 셀 케이지는 일부 오데에서 1,2,3,4의 값으로 구성되어야 한다).r. 알려진 최소 세포 범위는 필립 뉴먼이 제공한 18개의^[88] 세포로, 이것은 가능한 가장 적은 것으로 추측된다(17세포의 예는 현재 알려지지 않은 17-클루 고전적인 수도쿠를 암시한다).Philip Newman에 의해 제공되는,^[89] 알려진 우리들의 최소 수는 7개인데, 이것이 가능한지 가장 적은지는 알려져 있지 않다.

미유키 미사와의 웹사이트에^[90] 있는 변종은 합계를 관계로 대체한다: 단서들은 기호 =, <, >로 인접 지역 합계의 상대적 가치를 보여준다.그녀는 8가지 관계만으로 모범을 보여 준다.이것이 최선인지는 알 수 없다.

최대 기븐 수

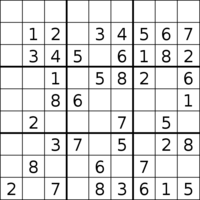
스도쿠를 최소화할 수 있는 가장 큰 단서는 40개로 추정되며, 이 중 단 2개만이 알려져 있다.만약 이들 수도쿠스 어느 하나에서 어떤 단서가 제거된다면, 퍼즐은 둘 이상의 해결책을 가지고 있을 것이다(따라서 제대로 된 수도쿠가 아니다).이러한 수도쿠스를 찾기 위한 작업에서는 36개의 단서를 가진 6억 5천만 개 이상의 최소 퍼즐을 포함한 다른 높은 클루 퍼즐이 목록화되었다.39개의 단서를 가진 약 2600개의 미니멀 수도쿠스도 발견되었다.^[91]

용액의 고유성 요건을 떨어뜨릴 경우 41클루 최소 사이비 퍼즐이 존재하는 것으로 알려져 있지만, 둘 이상의 용액 그리드로 완료할 수 있다.어떤 단서라도 제거하면 완성 횟수가 증가하며 이러한 관점에서 41개의 단서 중 어느 것도 중복되지 않는다.그리드의 절반 이상이 기븐으로 채워져 있는 상태에서(81개 셀 중 41개) 용액 제약의 고유성은 최소성 제약에 대해 여전히 지배적이다.^[92]

스도쿠에서 가능한 가장 많은 단서들에 대해서는, 여전히 독특한 해결책을 제시하지 않고, 풀 그리드(77)에 4가 부족하다.각각 두 개의 숫자로 된 두 개의 인스턴스가 누락되고 이들이 점유할 셀이 직교 사각형의 모서리이고, 이들 셀 중 정확히 두 개가 한 영역 내에 있는 경우, 마지막 숫자를 추가할 수 있는 두 가지 방법이 있다(해법 두 개).

최소 퍼즐 수

미니멀 수도쿠스(해결책의 고유성을 잃지 않고서는 어떤 단서도 지울 수 없는 스도쿠스)의 수는 정확히 알려지지 않았다.단, 발전기와 결합된 통계 기법('CSP – 제어-Bias 생성기의 불편 통계')^[93]은 대략 (상대 오차가 0.065%인)이 있음을 보여준다.

• 3.10 × 10 미니멀³⁷ 퍼즐,
• 2.55 × 10개의²⁵ 비응시 최소 퍼즐.

다른 저자들은 더 빠른 방법을 사용했고 추가적인 정밀한 분포 통계를 계산했다.^[94]

단서 기하학의 제약조건

적절한 스도쿠에게 불충분한 일련의 단서들.

30셀(5 x 6)의 빈 직사각형을 가진 스도쿠.(22개 단서)

9개의 빈 그룹이 있는 스도쿠.(22개 단서)

제대로 된 스도쿠는 위의 첫 번째 이미지의 선명한 공간에 위치의 범위에 한정된 단서를 가질 수 없다고 추측되어 왔다.^[95]적절한 스도쿠에서 가장 큰 직사각형 직사각형 "구멍"(단서가 없는 지역)은 30셀의 직사각형(5×6 직사각형 면적)으로 추정된다.^[96][97]한 예는 22개의 단서(두 번째 이미지)를 가진 스도쿠다.스도쿠에서 빈 그룹(행, 열, 상자)이 가장 많은 그룹은 9개로 추정된다.빈 행 3개, 빈 열 3개, 빈 상자 3개(제3 이미지)가 있는 스도쿠가 대표적이다.^[98][99]

오토모픽 수도쿠스

스도쿠 격자는 원래 격자로 다시 이어지는 방식으로 변환될 수 있다면 자동형이며, 다른 경우 같은 변환이 원래 격자로 다시 이어지지 않을 것이다.자동화된 그리드의 한 예는 180도 회전할 수 있는 그리드로, 새로운 셀 값이 원래 그리드의 순열인 새로운 그리드를 만들 수 있다.오토모픽 수도쿠스는 오토모픽 그리드로 해결하는 스도쿠 퍼즐이다.자동형 수도쿠스와 자동형 그리드의 두 가지 예가 아래에 제시되어 있다.

18개의 단서가 있는 오토모픽 스도쿠(양방향 대각선 대칭)[100]

24개의 단서(양방향 대각선 대칭, 변환 대칭)[101]를 가진 오토모픽 스도쿠

"Most Canonical" 솔루션 그리드(648개의 자동화)

각 그리드의 본질적으로 다른 그리드의 수
자동형성 계수

자동- 형태론	격자 번호	자동- 형태론	아니요. 격자무늬
1	5472170387	18	85
2	548449	27	2
3	7336	36	15
4	2826	54	11
6	1257	72	2
8	29	108	3
9	42	162	1
12	92	648	1

앞의 두 예에서 스도쿠가 180도 회전하고, 순열 (123456789) -> (987654321)와 다시 붙여진 단서가 같은 스도쿠로 되돌아간다는 점에 주목한다.다른 방식으로 표현하면, 이 수도쿠스는 180도 회전하는 한 쌍의 단서(a, b)마다 규칙(a) + (b) = 10을 따르는 속성을 가지고 있다.

이 수도쿠스는 자동형이기 때문에, 그들의 솔루션 그리드는 자동형이다.더욱이, 해결되는 모든 셀은 같은 기술로 해결되는 대칭적인 파트너를 가지고 있다(그리고 쌍은 + b = 10의 형태를 취한다).두 번째 예에서 스도쿠는 또한 변환(또는 반복) 대칭성을 보인다는 점에 유의하십시오. 단서는 그룹별로 군집화되어 있으며, 각 그룹의 단서는 순차적으로 정렬된다(즉, n, n+1, n+2, n+3).

세 번째 이미지는 Most Canonical 솔루션 그리드 입니다.^[102]이 그리드는 648개의 자동화를 가지며 비자동 그리드 대비 1/648의 비율로 모든 ~ 6.67×10²¹ 솔루션 그리드에 기여한다.

이러한 예에서 자동형은 식별하기 쉽지만, 일반적인 자동형은 항상 분명한 것은 아니다.오른쪽 표는 기존의 모든 자동화에 대해 본질적으로 다른 스도쿠 솔루션 그리드의 수를 보여준다.^[12]

고유 그리드 열거 세부사항(9×9)

연산 집약도가 현저히 떨어지는 밴드 생성을 기반으로 한 열거 기법이 개발되었다.전략은 유효 솔루션에 사용되는 탑 밴드의 순열을 분석하는 것으로 시작된다.부분 용액에 대한 Band1 대칭과 동등성 등급이 식별되면, 하위 두 대역의 보완이 구성되고 각 동등성 등급에 대해 계산된다.

상단 밴드 순열 계산

1	2	3
4	5	6
7	8	9

Band1 알고리즘은 다음과 같이 진행한다.

• B1에 값을 할당하여 자릿수에 대한 표준 라벨을 선택하고(그리드 참조), 나머지 Band1 순열 상대 B1을 계산한다.
• B2 행 트리플릿에 대해 B1 셀 값을 분할하여 B2의 순열을 계산한다.세 쌍의 조합에서 B2 순열을 계산한다.k=0이 있다.다음 3가지 방법을 선택하는 방법:

B2 r22에 대한 B1 r11 값, 나머지는 r16으로 가야 한다.

B2 r23에 대한 B1 r12 값, 나머지는 r16으로 가야 한다.

B2 r21에 대한 B1 r13 값, 나머지는 r16으로 가야 한다.

$B2}}=\sum _{k=0}^{3에 대한 {\displaystyle {\mbox{N 조합}{{3 \선택 k}^{3}}}$

(이 표현은 어떤 R×3 박스 밴드 변종에도 일반화될 수 있다. (페테르센^[31])따라서 B2는 56 × 6 순열에³ 기여한다.

• B3 삼중수소의 선택은 B1 B2 행 삼중수소에 의해 결정된다.B3는 항상 6개의³ 순열에 기여한다.

밴드1의 순열은 9! × 56 × 6⁶ = 9! × 2612736 ≈ 9.48×10이다¹¹.

밴드1순열내역

3중 rBR(상자/행) 레이블

r 1 1 r 1 2 r 1 3

r 2 1 r 2 2 r 2 3

r 3 1 r 3 2 r 3 3

B1의 순열은 9자리 숫자 9! = 362880을 다시 라벨링하는 방법의 수입니다.B2의 순열은 B1의 값에 따라 달라지기 때문에 계산이 더 복잡하다.(이것은 위에서 주어진 표현식의 시각적 표현이다)조건부 계산에는 각 대안에 대한 분기(하위 계산)가 필요하다.다행히 상위 B2 트리플트(r21)의 경우는 4개뿐인데, B1 중간 행 트리플트(r12)의 숫자 중 0, 1, 2, 3을 포함하고 있다.이 B2 상단 행을 선택하면 나머지 B2 조합이 고정된다.오른쪽에는 Band1 행 트리플트 라벨이 표시되어 있다.

(주: 조건부 조합은 그리드를 통해 연산이 진행됨에 따라 점점 더 어려워진다.이 시점에서 영향은 미미하다.)

케이스 0 매칭 셀 트리플릿

1 2 3 4 5 6 7 8 9

7 8 9 1 2 3 4 5 6

4 5 6 7 8 9 1 2 3

사례 0: 겹치지 않음.세 쌍둥이의 선택은 제거에 의해 결정될 수 있다.

r21은 r11 또는 r12일 수 없으므로 r13, r31은 r12 등이어야 한다.

사례 0 도표는 분홍색 셀이 트리플트 내에서 어떤 순서로 배열될 수 있는 트리플트 값인 이 구성을 보여준다.각각의 트리플렛은 3! = 6개의 순열이 있다.6쌍둥이는 6쌍둥이의⁶ 순열에 기여한다.

사례 3: 3자리 일치: 트리플t r21 = r12사례 0과 동일한 논리가 적용되지만 트리플릿 사용법은 다르다.트리플릿 r22는 = r13 등이어야 한다.순열 수는 다시 6⁶(펠겐하우어/자비스)이다.^[11]사례 0과 3을 순수한 일치 사례라고 부른다.

사례 1 매치 – 트리플릿 셀 옵션

1 2 3 4 5 6 7 8 9

3 3 2 1 3 2 1 2 1

3 2 1 3 2 1 3 2 1

사례 1: r12의 r21에 대해 1 일치

사례 1 다이어그램에서 B1 셀은 표준 값을 나타내며, B2 트리플릿에서 행-현 분포를 표시하기 위해 색상으로 구분된다.색은 분포를 반영하지만 위치나 값은 반영하지 않는다.이 경우: B2 상단 열 트리플릿(r21)은 B1 중간 트리플릿에서 1 값을 가지며, 다른 색상은 이제 추론할 수 있다.예: B2 아래쪽 행 트리플트(r23) 색상은 r21에 의해 강제 적용됨: 나머지 2 B1 중간 값은 아래로 가야 함 등각 색상에 대한 B2 옵션 수를 왼쪽 상단부터 입력하십시오.B3 선택사항은 B1, B2에 의해 행별로 결정되므로 B3 색상 코딩은 생략된다.B3는 항상 3행당 3행, 즉 블록당³ 6행의 순열에 기여한다.

B2의 경우, 트리플트 값이 어떤 위치에든 나타날 수 있으므로, 각 트리플트마다 3! 순열 계수가 적용된다.그러나 일부 값은 원점에 대해 쌍을 이루었기 때문에 원시 옵션 카운트를 사용하면 쌍 내의 상호 호환성으로 인해 순열 수를 초과하게 된다.옵션 카운트는 그룹화(2), 여기서 2! = 2( ${\displaystyle \genfrac{}{}{0ex}{}{\mathrm{참조}}{}}){\displaystyle }$로 나눌 필요가 있다. (n k${\displaystyle }$) ${\$ 각 행의 쌍은 B2 옵션 카운트에 대한 2s를 취소하여 3 × 6의³³ B2 기여를 남긴다.B2×B3 복합기여는 3³×6이다⁶.

사례 2 일치 – 트리플릿 셀 옵션

1 2 3 4 5 6 7 8 9

3 2 3 2 1 3 2 1 1

3 2 1 3 2 1 3 2 1

사례 2: r12의 r21에 대해 2 일치.사례 1과 동일한 논리가 적용되지만 B2 옵션 카운트 열 그룹화가 반전된 경우.사례 3은 또한 3³×6⁶ 순열에도 기여한다.

Band1 B1의 4가지 사례를 합치면..B3는 9! × 2 × (3³ + 1) × 6⁶ = 9! 56 × 6 순열을⁶ 부여한다.

밴드1 대칭 및 동등성 클래스

대칭은 Band1 순열을 열거하기 위한 계산 노력을 줄이기 위해 사용된다.대칭은 물체의 질을 보존하는 연산이다.스도쿠 그리드의 경우 대칭은 결과도 유효한 그리드인 변환이다.상단 대역에는 다음과 같은 대칭이 독립적으로 적용된다.

• 블럭 B1 값은 9! 순열로 다시 라벨링할 수 있음
• 블럭 B1..3은 교환할 수 있으며, 3!=6 순열
• 1행..3은 교환할 수 있으며, 3!=6 순열
• 각 블록 내에서 3개의 기둥을 상호 교환하여 3!³ = 6개의³ 순열을 제공할 수 있다.

대칭은 각 Band1 솔루션에 대해 9! × 6 = 362880⁵ × 7776 등가 순열을 부여한다.

대칭은 여기서 솔루션 사이의 동등성 관계를 정의하고 솔루션을 일련의 동등성 등급으로 분할한다.밴드1 행, 컬럼 및 블록 대칭은 ${\displaystyle 56}$× ${\displaystyle {6\mathrm{}}^{}}$ ${\$ 순열을$$ 각각 최대⁵ 6개의 순열이 있는 336 (56×6) 동등성 등급으로 나누고 각 클래스마다 9! 리마블링 순열로 나눈다.(일부 순열은 재실리로 인해 구별되는 요소가 발생하지 않을 수 있으므로 최소/최대 유의 사항이 적용된다.ng.)

동등 클래스의 모든 멤버에 대한 솔루션은 다른 멤버의 솔루션에서 생성될 수 있으므로, 모든 클래스에 걸쳐 모든 솔루션을 열거하려면 단일 멤버에 대한 솔루션만 열거하면 된다.내버려두다

• sb : 최고 밴드의 유효한 순열이다.
• Sb = [sb] : sb에 대한 동등성 등급이며, sb 및 일부
• Sb.z = Sb : Sb 크기 [sb]의 sb 요소 수(permutions)가 된다.
• Sb.n : Sb에 있는 (모든) sb에 대한 (band2,3)의 보완 수입니다.
• {Sb} : 동등성 관계에 상대적인 모든 Sb 동등성 클래스의 집합임
• {Sb.z = {Sb} : 동등성 클래스 수입니다.

총 솔루션 N 수는 다음과 같다.

N = σ{Sb} Sb.z × Sb.n

용액 및 계수 순열 대칭

Band1 대칭(위)은 순열 대칭으로, 순열 대칭은 순열 대칭으로, 순열 대칭은 순열 대칭이다.솔루션을 열거할 목적으로, 그리드 완성을 위한 계산 대칭은 최소 개수의 클래스를 생성하는 밴드 동등성 클래스를 정의하는데 사용될 수 있다.

대칭 칸막이를 계산하는 것은 하위 대역에 동일한 완성 제약을 두는 등급으로 유효한 Band1 순열이다; 대칭 동등성 등급 계산 대칭의 모든 멤버는 완료 제약조건이 동일하기 때문에 동일한 수의 그리드 보완을 가져야 한다.카운팅 대칭 제약조건은 Band1 컬럼 트리플릿(column value set, 암시적 요소 순서 없음)으로 식별된다.밴드 카운트 대칭을 사용하여 44개의 동등성 등급의^[56] 최소 생성 세트를 설정했다.

(1) Band1의 예 1 2 3 4 5 6 7 8 9 5 8 6 9 1 7 4 3 2 7 4 9 8 2 3 5 1 6

(2) 기둥 3중주 1 2 3 4 5 6 7 8 9 4 1 2 5 3 6 9 8 7 5 1 3 7 2 6 8 4 9

(3) 주문 콜. 1 2 3 4 5 6 7 8 9 1 3 5 2 6 7 4 9 8 1 2 4 3 6 5 8 7 9

다음 순서는 밴드 구성을 카운팅 대칭 동등성 등급에 매핑하는 것을 보여준다.유효한 대역 구성(1)으로 시작하십시오.각 열 내에 열 값을 정렬하여 열 세 개를 작성하십시오.이것은 유효한 스도쿠 대역은 아니지만, 예(2)와 같은 하한 대역의 제약을 두고 있다.B2, B3 열 트리플t 값에서 동등성 클래스 ID를 생성한다.칼럼과 박스 스왑을 사용하여 가장 낮은 사전 ID를 얻으십시오.마지막 그림은 ID의 컬럼과 박스 오더를 보여준다: 124 369 578 138 267 459.이 카운팅 대칭 ID를 가진 모든 밴드1 순열은 원래 예시와 동일한 수의 그리드 보완을 가질 것이다.이 프로세스의 확장은 대칭 등가 등급(3)을 계산할 수 있는 가능한 가장 큰 대칭 대칭 등가 등급을 만드는 데 사용될 수 있다.

참고, 동등성 클래스를 구성하고 식별하기 위해 컬럼 트리플릿을 사용하는 반면, 클래스 멤버 자체는 유효한 Band1 순열: 클래스 크기(Sb.z)는 One Rule 솔루션 요구사항에 적합한 컬럼 트리플릿 순열을 반영한다.대칭 계산은 완료 특성이며 부분 그리드(밴드 또는 스택)에만 적용된다.솔루션 보존을 위한 솔루션 대칭은 부분 그리드(밴드, 스택) 또는 전체 그리드 솔루션에 적용할 수 있다.마지막으로, 대칭 계산은 단순한 숫자 완성 계수 등식보다 더 제한적이다: 두 개의 (간결한) 대역은 동일한 계산 대칭 동등성 등급에 속하는데, 이는 동일한 완료 제약을 가하는 경우에만 해당된다.

밴드1감소내역

대칭은 유사한 개체를 동등성 클래스로 그룹화한다.동등성 등급과 여기서 사용되는 대역 대칭에 대해 두 개의 숫자를 구분해야 하며, 세 번째 숫자는 다음과 같다.

• 동등성 클래스 수({Sb.n).
• 등급에 따라 다를 수 있는 동등성 클래스의 카디널리티, 크기 또는 요소 수(Sb.z)
• Band1 동등성 클래스의 멤버와 호환되는 Band2,3의 개수(Sb.n)

밴드1(6⁵) 대칭은 (56×6⁶) 밴드1 유효 순열을 (56×6) 336 (56×6) 동등성 등급으로 나누고 각각 최대 () ${\displaystyle {6\mathrm{}}^{}}$ 5 ${\$ 6$^{5}$ 순열로$$ 나눈다.재구성이 필요한 경우 변환의 일부 조합은 뚜렷한 결과를 내지 못할 수 있으므로(아래 참조) 이상 주의사항이 필요하다.따라서 일부 동등성 등급은 6개⁵ 미만의 구별되는 순열을 포함할 수 있으며 이론적으로 최소 등급 수를 달성하지 못할 수 있다.

각각의 유효한 Band1 순열은 Band2,3 순열로 특정한 수의 솔루션으로 확장(완료)할 수 있다.유사성 때문에 동등성 등급의 각 구성원은 동일한 수의 보완을 가질 것이다.따라서 각 동등성 등급의 한 멤버에 대한 솔루션만 구성한 다음, 솔루션 수를 동등성 등급의 크기로 곱하면 된다.우리는 여전히 각 등가 등급의 크기를 파악하고 계산하는 과제를 남겨두고 있다.더 발전하려면 순열을 동등성 등급으로 분류(분류 및 계수)하기 위한 계산 기법의 능숙한 적용이 필요하다.

펠젠하우어/자르비스는^[11] B2,3 블록에서 순서가 지정된 숫자를 기준으로 사전 순서가 지정된 ID를 사용하여 밴드1 순열의 목록을 작성했다.블록 1은 표준 자릿수 할당을 사용하며 고유 ID에는 필요하지 않다.동등성 등급 식별 및 연결은 클래스 내에서 가장 낮은 ID를 사용한다.

(2×6²) B2,3 대칭 순열을 적용하면 각각 72 사이즈로 36288(28×6⁴) 동등성 등급이 생성된다.크기가 고정되어 있기 때문에 계산은 36288 동등성 등급 ID만 찾으면 된다(참고: 이 경우 Band1 순열의 경우, 가장 낮은 ID를 얻기 위해 이러한 순열을 적용하면 관련 동등성 등급에 지수를 제공한다).

블록, 열 및 행 대칭의 나머지 부분을 적용하여 36288개의 ID를 더 적은 수의 더 큰 동등성 등급으로 할당하는 등의 추가 감축을 제공했다.변환을 통해 B1 표준 라벨링이 손실되면 그 결과는 표준 B1 용도에 다시 첨부된 후 이 ID에 따라 분류된다.이 접근방식은 이론적 336개 최소 감축 한도보다 다소 덜 효과적인 416개의 동등성 등급을 생성했다.이중 쌍체 자릿수에 대한 대칭 패턴 계수 적용은 174개, 71개 등가 등급으로 감소하였다.밴드 카운트 대칭에 기초한 동등성 클래스의 도입(러셀의^[56] Felgenhauer/Jarvis에 이은 후속)은 동등성 클래스를 최소 생성 집합인 44개로 줄였다.

~2.6×10⁶, 56×6⁶ Band1 순열의 다양성은 44 Band1 동등성 등급의 집합으로 줄일 수 있다.44개의 등가 등급은 각각 수백만 개의 뚜렷한 풀 솔루션으로 확장할 수 있지만, 전체 솔루션 공간은 이 44개에서 공통적인 기원을 가지고 있다.44개의 등가 등급은 다른 열거형 접근법에서도 중심적인 역할을 하며, 추측은 나중에 퍼즐 특성을 탐구할 때 44개 등급의 특성으로 되돌아갈 것이다.

밴드 2-3 완료 및 결과

스도쿠 솔루션을 열거하는 것은 초기 설정 단계에 들어간 다음 두 개의 중첩된 루프로 나뉜다.처음에 모든 유효한 Band1 순열은 동등성 등급으로 분류되며, 각 등급은 Band2,3 보완에 공통적인 제약을 가한다.각 Band1 동등성 클래스에 대해 가능한 모든 Band2,3 솔루션을 열거해야 한다.외부 밴드1 루프는 44개의 동등성 클래스에 걸쳐 반복된다.내측 루프에서는 각 Band1 동등성 등급에 대한 모든 하부 밴드 보완을 찾아 카운트한다.

하부 밴드 솔루션 검색에 필요한 연산은 밴드1에 사용된 것과 동일한 유형의 대칭 어플리케이션으로 최소화할 수 있다.Band2,3의 1열에 6개의 값에 대한 6! (720) 순열이 있다.밴드(6×6) 순열 내에서 하위 밴드(2)와 행을 적용하면 72의 10개의 동등성 등급이 생성된다.이 시점에서 재귀 강하와 함께 나머지 48개 셀에 대해 10세트의 솔루션을 완성하면, 2GHz급 PC로 역추적 알고리즘이 가능하기 때문에 열거 수행에 추가적인 단순화가 필요하지 않다.이 접근법을 사용하여 빈 스도쿠 그리드를 채우는 방법의 수는 6,670,903,752,021,072,936,960(6.67×10²¹)인 것으로 나타났다.^[11]

Russell에 의해 확인된 결과에는 44개의 동등성 등급에 대한 솔루션 카운트의 분포도 포함된다.^[56]열거된 값은 9! 계수를 표지에 적용하기 전이고, 2개의 72계수(72² = 5184)는 스택 2,3과 밴드 2,3 순열 각각에 적용된다.클래스별 완료 횟수는 1억 건으로 일관하고, 클래스별로 적용되는 밴드1 순열 수는 4~3240회에서 차이가 있다.이 넓은 범위 안에 분명히 두 개의 군집이 있다.규모별로는 하위 33개 등급이 평균 400회 순열/클래스, 상위 11개 등급이 평균 ~2100회 순열이다.크기 및 완성 횟수에 대한 분포 간의 일관성 차이 또는 크기별 두 군집으로의 분리는 아직 조사되지 않았다.

참고 항목

• 콤비네이터 폭발 (라틴 사각형 대비 스도쿠 격자수 요약)
• 댄싱 링크스
• 스도쿠의 용어집
• 수도키안
• 스도쿠 코드

참조

추가 읽기

• Rosenhouse, Jason; Taalman, Laura (2011). Taking Sudoku Seriously: The math behind the world's most popular pencil puzzle. Oxford University Press.

외부 링크

• V. 엘서의 차이 맵 알고리즘도 스도쿠를 해결한다.
• 스도쿠 퍼즐 — Carsten Kehler Holst (Visual Prolog)의 구속조건 프로그래밍과 시각적 프롤로그 7 연습
• 헤르츠베르크와 머티의 스도쿠 스퀘어와 크로마틱 다항식들은 그래프 이론에서 스도쿠 퍼즐을 정점 색소 문제로 취급한다.