지도 접기

Map folding

종이접기 수학에서, 지도접기와 우표접기는 종이 한 장을 접을 수 있는 방법을 세는 두 가지 문제이다.우표 접기 문제에서 종이는 주름이 있는 우표 조각으로, 주름은 주름이 있는 곳에 놓여야 합니다.지도 접기 문제에서 종이는 주름을 기준으로 직사각형으로 나눈 지도이며, 주름은 다시 이 주름을 따라 있어야 합니다.

루카스(1891)는 우표 접기 문제의 발명을 에밀 르무아인의 [1]탓으로 돌린다.Touchard(1950)는 기타 몇 가지 초기 [2]레퍼런스를 제공합니다.

라벨 부착 스탬프

스탬프 접기 문제에서 접는 용지는 주름으로 구분된 정사각형 또는 직사각형 스탬프 조각으로, 스탬프는 주름에 따라 접을 수 밖에 없다.일반적으로 고려되는 문제의 한 가지 버전에서는 각 스탬프는 서로 구별할 수 있는 것으로 간주되기 때문에 스탬프 스트립의 두 개의 접힘은 [3]스탬프의 수직 시퀀스가 동일한 경우에만 동등하다고 간주됩니다.예를 들어, 3개의 다른 스탬프로 이루어진 스트립을 접는 방법에는 6가지가 있습니다.

Stampfoldings1x3.png

여기에는 스탬프의 6개 배열이 모두 포함되지만, 3개 이상의 스탬프의 경우 모든 배열이 가능한 것은 아닙니다.치환 p에 대해서, 패리티가 같은 2개의 숫자 i, j, i+1, j+1이 그 순환 순서로 p에 나타나도록 하면, p는 접을 수 없다.패리티 조건은 스탬프 i와 i + 1 사이의 주름과 스탬프 j와 j + 1 사이의 주름 사이에 접힌 스탬프 스택의 같은 쪽에 나타나는 것을 의미하지만 순환 순서 조건은 이러한 두 주름들이 서로 교차하는 것을 의미하므로 물리적으로 불가능합니다.예를 들면, 4극 치환 1324는, i=1, j=3의 금지 패턴을 가지고 있기 때문에, 접을 수 없다.이 패턴이 없는 나머지 순열은 모두 [3]접을 수 있습니다.n개의 스탬프 스트립을 접는 다양한 방법의 수는 시퀀스에 의해 지정된다.

1, 2, 6, 16, 50, 144, 462, 1392, 4536, 14060, 46310, 146376, 485914, 1557892, 5202690, ...(OEIS의 시퀀스 A000136).

이 숫자들은 항상 n으로 나눌 수 있다(접이식 스탬프 시퀀스의 순환 배열은 항상 접을 [3][4]수 있기 때문에). 그리고 이 중분류의 몫은 다음과 같다.

1, 1, 2, 4, 10, 24, 66, 174, 504, 1406, 4210, 12198, 37378, 111278, 346846, 1053874, ...(OEIS의 시퀀스 A000682),

반각 곡선이 "반각 곡선"이라고 불리는 선과 n개의 교차를 만들 수 있는 위상적으로 구별되는 방법의 수.

수학의 미해결 문제:

스탬프 폴딩 문제에 대한 해결책을 세는 공식이나 다항식 시간 알고리즘이 있습니까?

(수학에서 풀리지 않은 문제가 더 많다)

1960년대에 존 E.Koehler와 W. F. Lunnon은 당시 최대 28개의 [5][6][7]스탬프에 대해 이러한 수치를 계산할 수 있는 알고리즘을 구현했습니다.추가 연구에도 불구하고, 이러한 수치를 계산하는 알려진 방법은 [8][9]n의 함수로서 기하급수적인 시간이 걸린다.따라서 이 시퀀스를 n의 매우 큰 값으로 확장할 수 있는 공식이나 효율적인 알고리즘은 알려져 있지 않습니다.그럼에도 불구하고, 물리학의 발견적 방법은 이 [10]시퀀스의 지수적 성장률을 예측하기 위해 사용될 수 있다.

스탬프 폴딩 문제는 일반적으로 스탬프 스트립의 가능한 폴딩 상태의 수만을 고려하며, 전개된 스탬프 스트립에서 시작하는 일련의 움직임에 의해 물리적으로 폴딩을 구성할 수 있는지 여부를 고려하지 않습니다.그러나 목수 규칙 문제의 해법에 따라 접힌 모든 상태를 구성할 수 있다(또는 동등한 방법으로 [11]전개할 수 있다).

라벨이 붙어 있지 않은 스탬프

스탬프 접기 문제의 또 다른 변형에서는 스탬프 스트립이 공백으로 간주되어 한쪽 끝을 구별할 수 없고, 두 개의 접기는 모양이 다른 경우에만 구별되는 것으로 간주한다.접힌 스트립을 뒤집거나 앞뒤로 돌려도 모양이 바뀌지 않으므로 세 개의 스탬프는 S-곡선과 [3]나선형의 두 개의 접힘만 있습니다.보다 일반적으로, 이 정의를 가진 접힘의 수는 다음과 같습니다.

1, 1, 2, 5, 14, 38, 120, 353, 1148, 3527, 11622, 36627, 121622, 389560, 1301140, 4215748, ...(OEIS의 시퀀스 A001011)

지도

지도 접기는 각각의 주름을 산이나 계곡으로 만들 수 있는 직사각형 지도를 접는 방법이 얼마나 많은지에 대한 문제입니다.스탬프 폴딩과 다른 점은 한 [12]방향으로만 주름이 잡히는 것이 아니라 가로와 세로 모두 주름이 잡히는 것입니다.

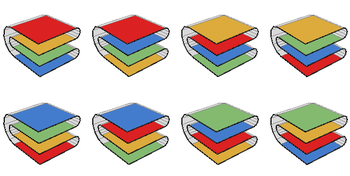
2 × [5]2 지도를 접는 방법에는 8가지가 있으며 접힌 정사각형의 서로 다른 수직 시퀀스를 지도를 접는 고유한 방법으로 간주한다.

MapFoldings-2x2.png

그러나 지도를 접는 방법의 수를 세는 일반적인 문제는 아직 해결되지 않았다.n × n 지도를 접는 방법의 수는 n 7 7에 대해서만 알려져 있다.다음과 같은 것이 있습니다.

1, 8, 1368, 300608, 186086600, 123912532224, 129950723279272(OEIS의 시퀀스 A001418).

복잡성

수학의 미해결 문제:

지도의 주름에 대한 산골짜기 과제를 지정하면, 평탄하게 접을 수 있는지 여부를 효율적으로 테스트할 수 있습니까?

(수학에서 풀리지 않은 문제가 더 많다)

지도 접기와 스탬프 접기 문제는 종이접기 수학에서 주름 무늬가 있는 정사각형을 접을 수 있는지 여부와 관련이 있다.스탬프 스트립의 각 주름에 접는 방향(산지 또는 계곡 접힘)을 지정하면 결과가 다항식 [13]시간에 평평하게 접힐 수 있는지 테스트할 수 있다.

지도에서 동일한 문제(주름에 의해 직사각형으로 구분됨)에 대해 다항식 시간 접기 알고리즘이 일반적으로 존재하는지 여부는 알 수 없지만, 2 × n [14]지도에 대해 다항식 알고리즘이 알려져 있다.지도를 한 줄로 접는 "단순" 접기 순서로 접는 제한된 경우 문제는 다항식입니다.예를 들어 직사각형이 아닌 용지에 대한 문제의 확장은 NP-완전입니다.[13]

1차원 우표도 주름이 산이나 계곡의 접힘이라는 라벨이 붙어 있기 때문에 [15]접을 수 있는 방법을 찾기가 어렵다.

「 」를 참조해 주세요.

레퍼런스

  1. ^ 를 클릭합니다Lucas, Édouard (1891), Théorie des nombres (in French), vol. I, Paris: Gauthier-Villars, p. 120.
  2. ^ 를 클릭합니다Touchard, Jacques (1950), "Contribution à l'étude du problème des timbres poste", Canadian Journal of Mathematics (in French), 2: 385–398, doi:10.4153/CJM-1950-035-6, MR 0037815.
  3. ^ a b c d Legendre, Stéphane (2014), "Foldings and meanders", The Australasian Journal of Combinatorics, 58: 275–291, arXiv:1302.2025, Bibcode:2013arXiv1302.2025L, MR 3211783
  4. ^ Legendre(2014Sainte-Laguë, André (1937), Avec des nombres et des lignes (in French), Paris: Vuibert, pp. 147–162)가 인용한 바와 같이
  5. ^ a b 특히 페이지 60~62를 참조하십시오Gardner, Martin (1983), "The combinatorics of paper folding", Wheels, Life and Other Mathematical Amusements, New York: W. H. Freeman, pp. 60–73, Bibcode:1983wlom.book.....G.
  6. ^ Koehler, John E. (1968), "Folding a strip of stamps", Journal of Combinatorial Theory, 5 (2): 135–152, doi:10.1016/S0021-9800(68)80048-1, MR 0228364
  7. ^ Lunnon, W. F. (1968), "A map-folding problem", Mathematics of Computation, 22 (101): 193–199, doi:10.2307/2004779, JSTOR 2004779, MR 0221957
  8. ^ Jensen, Iwan (2000), "A transfer matrix approach to the enumeration of plane meanders", Journal of Physics A: Mathematical and General, 33 (34): 5953, arXiv:cond-mat/0008178, Bibcode:2000JPhA...33.5953J, doi:10.1088/0305-4470/33/34/301, S2CID 14259684
  9. ^ Sawada, Joe; Li, Roy (2012), "Stamp foldings, semi-meanders, and open meanders: fast generation algorithms", Electronic Journal of Combinatorics, 19 (2): Paper 43, 16pp, doi:10.37236/2404, MR 2946101
  10. ^ Di Francesco, P. (2000), "Exact asymptotics of meander numbers", Formal power series and algebraic combinatorics (Moscow, 2000), Springer, Berlin, pp. 3–14, doi:10.1007/978-3-662-04166-6_1, ISBN 978-3-642-08662-5, MR 1798197
  11. ^ Connelly, Robert; Demaine, Erik D.; Rote, Günter (2003), "Straightening polygonal arcs and convexifying polygonal cycles" (PDF), Discrete and Computational Geometry, 30 (2): 205–239, doi:10.1007/s00454-003-0006-7, MR 1931840
  12. ^ Lunnon, W. F. (1971), "Multi-dimensional map-folding", The Computer Journal, 14: 75–80, doi:10.1093/comjnl/14.1.75, MR 0285409
  13. ^ a b 를 클릭합니다Arkin, Esther M.; Bender, Michael A.; Demaine, Erik D.; Demaine, Martin L.; Mitchell, Joseph S. B.; Sethia, Saurabh; Skiena, Steven S. (September 2004), "When can you fold a map?" (PDF), Computational Geometry: Theory and Applications, 29 (1): 23–46, doi:10.1016/j.comgeo.2004.03.012.
  14. ^ Morgan, Thomas D. (May 21, 2012), Map folding (Thesis), Master's thesis, Massachusetts Institute of Technology, Department of Electrical Engineering and Computer Science, hdl:1721.1/77030
  15. ^ Umesato, Takuya; Saitoh, Toshiki; Uehara, Ryuhei; Ito, Hiro; Okamoto, Yoshio (2013), "The complexity of the stamp folding problem", Theoretical Computer Science, 497: 13–19, doi:10.1016/j.tcs.2012.08.006, MR 3084129

외부 링크