리마송

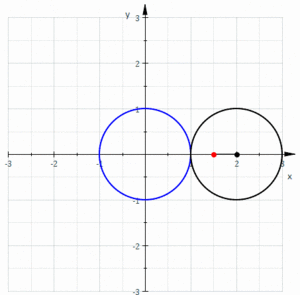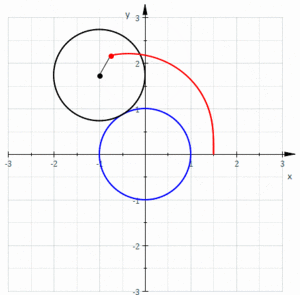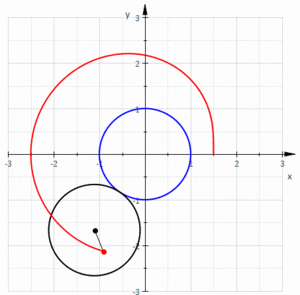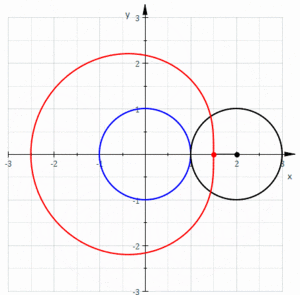
기하학에서 리마콘 또는 리마콘 / ˈ ɪ ɒ ən/는 파스칼 또는 파스칼의 스네일의 리마콘이라고도 하며, 원이 등반지름의 원의 바깥쪽을 돌 때 원에 고정된 점의 경로에 의해 형성되는 룰렛 곡선으로 정의됩니다. 작은 원이 큰 원 안에 들어가도록 반지름이 절반인 원을 돌 때 만들어지는 룰렛이라고 정의할 수도 있습니다. 따라서 그들은 중심 트로코이드라고 불리는 곡선 계열에 속합니다. 더 구체적으로는 에피트로코이드입니다. 카디오이드(cardioid)는 룰렛을 생성하는 점이 구르는 원 위에 놓여 있는 특별한 경우입니다. 결과적인 곡선에는 첨두가 있습니다.

곡선을 생성하는 점의 위치에 따라 내부 루프와 외부 루프가 있을 수 있으며(군명을 지정함), 하트 모양일 수도 있고 타원형일 수도 있습니다.

리마손(limaçon)은 4도의 쌍원 유리 평면 대수 곡선입니다.

세 개의 리마손: 보조개, cusp(심장근종), looped. 표시되지 않음: 볼록한 리마손

역사

리마송에 대한 최초의 공식적인 연구는 일반적으로 블레즈 파스칼의 아버지인 에티엔 파스칼에 기인합니다. 그러나 독일 르네상스 시대의 예술가 알브레히트 뒤러는 이 작품들에 대한 통찰력 있는 조사를 진행했습니다. 뒤러의 Underweysung der Messung(측정법)에는 리마송을 생산하기 위한 구체적인 기하학적 방법이 포함되어 있습니다. 그 곡선은 Gilles de Roberval이 접선을 찾는 예로 사용했을 때 이름 지어졌습니다.

방정식

극좌표에서 리마손의 방정식은 다음과 같은 형태를 갖습니다.

r=b+a\cos \theta.

이것은 r을 곱하여 데카르트 좌표로 변환할 수 있습니다(어떤 경우에는 가짜인 원점에 점을 도입하는 thus). r 2 = $r^{2}=x^{2}+y^{2}$ x $r^{2}=x^{2}+y^{2}$ + $r^{2}=x^{2}+y^{2}$ 2 {\ $display$ r^{2} = x^{2}+ y^{2}}와 r cos ⁡ θ = x {\display r\cos \theta = x}를 $r^{2}=x^{2}+y^{2}$ 하면 다음을 얻을 수 있습니다.

\left(x^{2}+y^{2}-ax\right)^{2}=b^{2}\left(x^{2}+y^{2}\right).

극값의 매개변수 형식을 데카르트 변환에 적용하면, 우리는 또한^[2]

x=(b+a\cos \theta )\cos \theta ={a \over 2}+b\cos \theta +{a \over 2}\cos 2\theta,

y=(b+a\cos \theta)\sin \theta = b\sin \theta +{a \over 2}\sin 2\theta;

세팅을 하면서

z=x+iy=(b+a\cos \theta )(\cos \theta +i\sin \theta )

복소 평면에서 곡선으로 다음 매개변수화를 산출합니다.

z={a \over 2}+be^{i\theta }+{a \over 2}e^{2i\theta }.

만약 ${\textstyle -{\frac {1}{2}}a}$ 수평으로 이동한다면 ${\textstyle -{\frac {1}{2}}a}$ {\ $textstyle -{\frac {1}{2}}a$ 즉,

z=be^{it}+{a \over 2}e^{2it}

=

be

+ a 2 e 2 it {\displaystyl

z=be^{it}+{a \over 2}e^{2it}

z = be^{it}+{a \over 2} e^{2it}},

원점의 위치를 변경함으로써, 우리는 중심 트로코이드의 방정식의 일반적인 형태로 변환할 것입니다. 이 시점에서 독립 변수의 변경을 기록하여 기본 극좌표 매개 변수화 θ = $\theta =\arg z$ ⁡ z {\displaystyle \theta =\arg z}를 더 이상 사용하지 않음을 분명히 합니다.

특수한 경우

특수한 경우 $a=b$ = ${\$ displaystyle a = b}에서 극 방정식은

r=b(1+\cos \theta )=2b\cos ^{2}{\frac {\theta }{2}}

아니면

r^{1 \over 2}=(2b)^{1 \over 2}\cos {\frac {\theta}{2}

사인 곡선의 나선형 곡선군의 일원으로 만드는 것입니다. 이 곡선이 심장병입니다.

특수한 $a=2b$ $a=2b$ = $a=2b$ b $a=2b$ {\displaystyle a = 2b}에서 방정식의 중심 트로코이드 형태는

z=b\left(e^{it}+e^{2it}\right)=be^{3it \over 2}\left(e^{it \over 2}+e^{-it \over 2}\right)=2be^{3it \over 2}\cos {t \over 2}

또는 극좌표에서,

r=2b\cos {\theta \over 3}

장미 곡선 계열의 일원으로 만드는 것입니다. 이 곡선은 삼등분선이며, 때때로 리마손 삼등분선이라고도 합니다.

형태

$b>a$ > $b>a$ $b>a$ 일 때 리마손은 단순 폐곡선입니다 $b>a$ 그러나 원점은 위에 주어진 데카르트 방정식을 만족하므로 이 방정식의 그래프는 교점 또는 고립점을 갖습니다.

$b>2a$ > $b>2a$ $b>2a$ ${\displaystyle$ b> $2a$ 일 때 곡선으로 경계지어지는 영역은 볼록하고, $a<b<2a$ < $a<b<2a$ < $a<b<2a$ a $a<b<2a$ {\ $displaystyle a< b< 2a$ 일 때 곡선은 2개의 변곡점으로 경계지어지는 만입부를 갖습니다. $b=2a$ = $b=2a$ $b=2a$ {\ $displaystyle$ b = 2a}에서 점 ( - a, 0 ) {\displaystyle (-a, 0)}은 0 곡률의 점입니다.

$b$ ${\displaystyle$ b $}$ 이 $($ 가) {\ $displaystyle$ a $}$ 에 비해 감소함에 $a$ 따라 $b=a$ = ${\$ displaystyle b=a}에서 곡선이 cardioid가 되고 만입이 cusp가 될 때까지 만입이 더 뚜렷해집니다. $0<b<a$ < $0<b<a$ < ${\displaystyle$ 0 < $b$ < $a}$ 의 경우 $0<b<a$ cusp가 내부 루프로 확장되고 곡선이 원점에서 교차합니다. $b$ $b$ 가 0에 $b$ 가까워지면 루프가 외부 곡선을 채우고 한계에서는 리마손이 두 번 횡단하는 원이 됩니다.

측정.

리마송 $r=b+a\cos \theta$ = $b$ + a cos ⁡ θ {\displaystyle r = b+a\cos \theta}로 둘러싸인 영역은 (b 2 + a 22) π {\textstyle \left(b^{2}+{a^{2} \over 2}\right)\pi}입니다. b < a < {\displaystyle b<a}일 때 내부 루프로 둘러싸인 영역을 두 번 계산합니다. 이 경우 곡선이 원점을 ${\textstyle \pi \pm \arccos {b \over a}}$ π ± arcos ${\textstyle \pi \pm \arccos {b \over a}}$ ⁡ $b {\textstyle \pi \pm \arcos$ {b \over a}} 각도로 교차합니다. 내부 루프로 둘러싸인 영역은

\left(b^{2}+{a^{2}}\over2}\right)\arccos {b \over a}-{3 \over2}b{\sqrt {a^{2}-b^{2}}

외부 루프로 둘러싸인 영역은

\left(b^{2}+{a^{2}}\over2}\right)\left(\pi -\arccos {b \over a}\right)+{3 \over2}b{\sqrt {a^{2}-b^{2}}

그리고 루프 사이의 영역은

{\displaystyle \left(b^{2}+{a^{2}}\over2}\right)\left(\pi-2\arccos {b \over a}\right)+3b{\sqrt {a^{2}-b^{2}}}.

^[1]

리마손의 둘레는 두 번째 종류의 완전한 타원 적분으로 주어집니다.

4(a+b)E\left({2{\sqrt {ab}} \over a+b}\right)}

다른 곡선과의 관계

$P$ $P$ 를 $P$ 점이라 하고 C ${\displaystyle$ C $}$ 를 $C$ $P$ 이 P{\ $displaystyle$ P}가 아닌 원이라 하자 $P$ 그러면 중심이 $C$ ${\displaystyle$ C $} 위$ 에 있고 $C$ P $P$ 를 통과하는 원들의 봉투는 $P$ 리마송입니다.

원의 페달은 리마손입니다. 실제로 반지름 $b$ 가{\ $displaystyle b}$ 이고 중심이 ( $(a,0)$ 0 $)$ {\ $displaystyle (a, 0)}$ 인 원 원점에 대한 페달은 극방정식 $r=b+a\cos \theta$ = $r=b+a\cos \theta$ + $r=b+a\cos \theta$ cos ⁡ θ {\displaystyle r = b+a\cos \theta }를 갖습니다.

$r=b+a\cos \theta$ = $r=b+a\cos \theta$ + $r=b+a\cos \theta$ a cos ⁡ θ {\displaystyle r = b+a\cos \theta}의 단위 원에 대한 역수는

r={1 \over {b+a\cos \theta}}

이는 이심률

{\tfrac {a}{b}}

{\displaystyle

{\tfrac {a}{

b}}

이고

{\tfrac {a}{b}}

원점에 초점이 있는 원뿔 단면의 방정식입니다. 따라서 리마손은 반전의 중심이 초점 중 하나인 원뿔의 역으로 정의될 수 있습니다. 원뿔이 포물선인 경우 역방향은 심장형이고, 원뿔이 쌍곡선인 경우 해당 리마손은 내부 루프를 가지며, 원뿔이 타원인 경우 해당 리마손은 루프가 없습니다.

원 위의 한 점에 대한 원의 콘코이드는 리마손입니다.

데카르트 타원형의 특별한 경우는 리마손입니다.^[3]

참고 항목

참고문헌

^ ^a ^b J. Dennis Lawrence (1972). A catalog of special plane curves. Dover Publications. pp. 113–118. ISBN 0-486-60288-5.
^ 바이스타인, 에릭 W "리마손" From MathWorld--Wolfram Web Resource.
^ O'Connor, John J.; Robertson, Edmund F., "Cartesian Oval", MacTutor History of Mathematics Archive, University of St Andrews

외부 링크

[Lawrence-1] J. Dennis Lawrence (1972). A catalog of special plane curves. Dover Publications. pp. 113–118. ISBN 0-486-60288-5.

[Weisstein-2] 바이스타인, 에릭 W "리마손" From MathWorld--Wolfram Web Resource.

[3] O'Connor, John J.; Robertson, Edmund F., "Cartesian Oval", MacTutor History of Mathematics Archive, University of St Andrews

[2]

[1]

[3]

Search

리마송

네임스페이스

더

목차

역사

방정식

특수한 경우

형태

측정.

다른 곡선과의 관계

참고 항목

참고문헌

더보기

외부 링크