트리(데이터 구조)
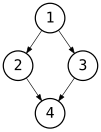
Tree (data structure)컴퓨터 과학에서 트리는 연결된 노드 집합이 있는 계층 트리 구조를 나타내는 널리 사용되는 추상 데이터 유형입니다.트리의 각 노드는 트리 유형에 따라 여러 하위 노드에 연결할 수 있지만 상위 노드가 없는 루트 노드를 제외하고 정확히 하나의 상위 노드에 연결해야 합니다.이러한 제약조건은 사이클이나 "루프"가 없음을 의미하며(어떤 노드도 자신의 조상이 될 수 없음), 또한 각 아이는 자신의 하위 트리의 루트 노드처럼 취급될 수 있으므로 재귀는 트리 트래버설에서 유용한 기술입니다.선형 데이터 구조와는 달리 많은 트리는 단일 직선으로 인접 노드 간의 관계로 나타낼 수 없습니다.
이진 트리는 일반적으로 사용되는 유형으로, 각 부모의 자녀 수를 정확히 두 개로 제한합니다.하위의 순서가 지정되면 이 데이터 구조는 그래프 이론의 순서 트리에 해당합니다.다른 데이터에 대한 값 또는 포인터는 트리 내의 모든 노드에 관련지을 수 있으며, 때로는 하위 노드가 없는 리프 노드에만 관련지을 수 있습니다.
추상 데이터 유형은 자녀에 대한 포인터를 가진 부모 목록, 부모에 대한 포인터를 가진 자녀 목록 또는 노드 목록과 부모-자녀 관계의 개별 목록(특정 유형의 인접 목록) 등 다양한 방법으로 나타낼 수 있습니다.표현은 더 복잡할 수 있습니다. 예를 들어 성능을 위해 인덱스 또는 상위 목록을 사용합니다.
컴퓨팅에 사용되는 나무는 그래프 이론의 나무, 집합 이론의 나무, 기술 집합 이론의 나무의 수학적 구조와 비슷하지만 다를 수 있습니다.
적용들
트리는 일반적으로 다음과 같은 응용 프로그램에서 계층 데이터를 나타내거나 조작하는 데 사용됩니다.
- 파일 시스템:
- 객체 지향 프로그래밍에서 클래스 간의 관계를 보여주는 클래스 계층 또는 "상속 트리"입니다. 다중 상속은 트리 이외의 그래프를 생성합니다.
- 컴퓨터 언어의 추상 구문 트리
- 자연어 처리:
- XML 및 HTML 문서의 문서 객체 모델("DOM 트리")
- 검색 트리는 트리 트래버설을 통해 효율적인 검색 알고리즘을 가능하게 하는 방식으로 데이터를 저장합니다.
- 정렬된 데이터 목록 표시
- 컴퓨터 생성 이미지:
- 반즈 저장 -은하 시뮬레이션에 사용되는 오두막 나무
- 무더기 도입
- 중첩된 세트
- Dewey Decimal Classification(듀이 십진분류법)과 같은 계층적 분류법.
- 계층형 시간 메모리
- 유전자 프로그래밍
- 계층 클러스터링
트리는 다음과 같은 다양한 수학적 구조를 표현하고 조작하는 데 사용할 수 있습니다.
트리 구조는 종종 다음과 같은 사물 간의 관계를 매핑하는 데 사용됩니다.
- 분해도에서 시각화할 수 있는 구성요소 및 하위 구성요소
- 프로그램에서 다른 서브루틴을 비재귀적으로 호출하는 서브루틴을 식별하는 데 사용되는 서브루틴 호출
- 진화, 소프트웨어 프로젝트에 의한 소스 코드(예: Linux 배포 타임라인), 다양한 종류의 자동차 디자인 등에 의한 종 간의 DNA 상속.
- 계층 네임스페이스의 내용
JSON 및 YAML 문서는 트리로 간주할 수 있지만 일반적으로 중첩된 목록 및 사전으로 표시됩니다.
용어.
노드는 데이터와 다른 노드(에지 또는 링크라고도 함)에 대한 연결을 포함할 수 있는 구조입니다.트리의 각 노드에는 트리의 하위 노드 아래에 0개 이상의 하위 노드가 있습니다(일반적으로 트리는 하위 노드를 아래로 하여 그려집니다).하위 노드가 있는 노드를 하위 노드(또는 상위 노드)라고 합니다.최상위 루트 노드를 제외하고 모든 노드에는 정확히 하나의 상위 노드가 있습니다.노드에는 상위 노드(예: 상위 노드)가 많을 수 있습니다.부모가 같은 하위 노드는 형제 노드입니다.일반적으로 형제자매는 순서가 있는데, 첫 번째 순서는 일반적으로 왼쪽에 그려집니다.일부 정의에서는 트리에 노드가 전혀 없는 것을 허용합니다.이 경우 트리는 비어 있습니다.
내부 노드(inner node, 줄여서 inode, branch node라고도 함)는 하위 노드를 가진 트리의 노드입니다.마찬가지로 외부 노드(외부 노드, 리프 노드 또는 터미널 노드라고도 함)는 자녀 노드가 없는 노드입니다.
노드의 높이는 해당 노드에서 리프까지의 가장 긴 하향 경로 길이입니다.뿌리의 높이는 나무의 높이입니다.노드의 깊이는 루트에 대한 경로 길이(루트 경로)입니다.제로 베이스 카운트를 사용하는 경우 루트노드는 깊이 0, 리프노드는 높이 0, 단일 노드(루트와 리프 모두)만 있는 트리에는 깊이 0이 됩니다.일반적으로 빈 트리(노드가 없는 트리, 가능하면 노드 없음)의 높이는 -1입니다.
각 비루트 노드는 해당 노드와 모든 하위 [a][1]노드를 포함하는 자체 하위 트리의 루트 노드로 취급할 수 있습니다.
트리와 함께 사용되는 다른 용어:
- Neighbor
- 부모 또는 자녀
- Ancestor
- 하위에서 상위로 반복하여 도달 가능한 노드입니다.
- Descendant
- 부모에서 자녀로 반복 처리하여 도달할 수 있는 노드입니다.서브차일드라고도 합니다.
- Degree
- 특정 노드에 대한 하위 노드 수입니다.잎은 반드시 0도를 가진다.
- Degree of tree
- 트리의 정도는 트리에 있는 노드의 최대 수준입니다.
- Distance
- 두 노드 사이의 최단 경로를 따른 에지 수입니다.
- Level
- 노드의 레벨은 노드와 루트 [2]노드 사이의 고유 경로를 따라 있는 에지 수입니다. 이것은 제로 베이스 카운트를 사용하는 경우의 깊이와 동일합니다.
- Width
- 레벨 내의 노드 수.
- Breadth
- 잎의 수
- Forest
- 하나 이상의 분리된 트리 집합입니다.
- Ordered tree
- 각 정점의 자식에 대해 순서가 지정된 루트 트리입니다.The Art of Computer Programming이라는 책은 지향적인 [3]나무라는 용어를 사용한다.
- Size of a tree
- 트리의 노드 수.
트리 및 비트리의 예
공통 조작
| 그래프와 트리 검색 알고리즘 |
|---|
| 최단 경로 |
| 리스트 |
| 관련 토픽 |
- 모든 항목을 열거하는 중
- 트리의 섹션 열거
- 아이템 검색
- 트리의 특정 위치에 새 항목 추가
- 항목 삭제
- 프루닝:트리의 전체 섹션 제거
- 접목:트리에 전체 섹션 추가
- 임의의 노드의 루트 찾기
- 두 노드의 가장 낮은 공통 조상 찾기
트래버설 및 검색
부모와 자녀 사이의 연결을 통해 나무의 항목을 밟는 것을 나무 걷기라고 하며, 그 행동은 나무 걷기이다.포인터가 특정 노드에 도착했을 때 작업이 수행될 수 있습니다.각 부모 노드가 자식보다 먼저 횡단되는 워크를 사전순서 워크라고 합니다.자녀가 각각의 부모를 횡단하기 전에 횡단되는 워크를 사후 워크라고 합니다.노드의 왼쪽 서브트리, 노드 자체, 마지막으로 오른쪽 서브트리가 횡단되는 워크를 순차 트래버설이라고 합니다.(이 마지막 시나리오는 왼쪽 서브트리와 오른쪽 서브트리의 정확히2개의 서브트리를 참조하고 있으며, 특히 바이너리 트리를 상정하고 있습니다).레벨 순서 워크는 효과적으로 트리 전체에 대해 폭 우선 검색을 수행합니다.노드는 레벨별로 트래버스되며, 여기서 루트 노드와 그 형제자매가 먼저 방문되고, 이어서 트리의 모든 노드가 트래버스될 때까지 그 자녀 노드와 그 형제자매가 차례로 방문됩니다.
표현
나무를 표현하는 방법에는 여러 가지가 있다.작업 메모리에서 노드는 일반적으로 자식, 부모 또는 둘 다에 대한 포인터와 함께 연관된 데이터를 사용하여 동적으로 할당됩니다.크기가 고정된 경우 노드가 목록에 저장될 수 있습니다.노드 및 노드 간의 관계는 별도의 특수한 유형의 인접 목록에 저장될 수 있습니다.관계형 데이터베이스에서 노드는 일반적으로 테이블 행으로 표시되며 상위 행과 하위 행 사이의 포인터를 용이하게 하는 인덱스 행 ID가 있습니다.
노드도 배열 내의 항목으로 저장할 수 있으며 노드 간의 관계는 배열 내의 위치에 따라 결정됩니다(바이너리 힙).
바이너리 트리는 리스트의 리스트로서 실장할 수 있습니다.목록의 선두(제1항의 값)는 왼쪽 자식(서브트리)이며, 테일(제2항 이후의 용어 리스트)은 오른쪽 자식(서브트리)입니다.이 값은 Lisp S 식에서도 변경할 수 있습니다.Lisp S 식에서는 헤드(첫 번째 항의 값)는 노드의 값, 테일(두 번째 항의 값)은 왼쪽 자식, 테일(세 번째 이후의 항의 목록)은 오른쪽 자식입니다.
순서가 매겨진 트리는 유한한 시퀀스(예: 자연수)[4]로 자연스럽게 부호화할 수 있습니다.
유형 이론
추상 데이터 타입으로서 추상 포레스트 타입 F(트리 리스트)를 사용하여 다음과 같은 함수에 의해 어떤 타입 E의 값을 갖는 추상 트리 타입 T를 정의한다.
- 값: T → E
- 아이:T → F
- 0: () → F
- 노드: E × F → T
다음 공리와 함께:
- 값(node(e, f)) = e
- children(node(e, f)) = f
유형 이론의 관점에서 트리는 생성자 0(빈 포레스트)과 노드( 주어진 값과 하위 값을 가진 루트 노드를 가진 트리)에 의해 정의된 유도형입니다.
수리 용어
전체적으로 볼 때 트리 데이터 구조는 일반적으로 각 노드에 값이 부가된 순서 트리입니다.구체적으로는 다음과 같습니다(공백하지 않아야 하는 경우).
- "뿌리에서 멀리" 방향을 가진 루트 트리(더 좁은 용어는 "arborescence")는 다음을 의미합니다.
- 특정 노드의 하위 노드에 대한 순서 지정
- (일부 데이터 유형의) 값을 지정합니다.
종종 트리는 고정(더 적절하게, 경계) 분기 계수를 가지며, 특히 항상 두 개의 하위 노드(아마도 비어 있을 수 있으므로 최대 두 개의 비어 있지 않은 하위 노드)를 가지므로 "이진수 트리"가 됩니다.
빈 트리를 허용하면 정의가 심플해지고 더 복잡해집니다.루트 트리는 비어 있지 않아야 합니다.따라서 위의 정의가 "빈 트리 또는 그와 같은 루트 트리"가 됩니다.한편 빈 트리는 고정된 분기 계수를 정의하는 것을 단순화합니다.빈 트리가 허용되면 이진 트리는 트리입니다.각 노드에는 정확히 2개의 자녀가 있으며 각각이 트리(빈칸)입니다.트리의 전체 작업 집합에는 포크 [clarification needed]작업이 포함되어야 합니다.
「 」를 참조해 주세요.
메모들
- ^ 이것은 그래프 이론에서 사용되는 하위 트리의 공식 정의와 다릅니다. 하위 트리는 트리를 형성하는 하위 그래프입니다. 모든 하위 트리를 포함할 필요는 없습니다.예를 들어 루트 노드 자체는 그래프 이론의 의미에서는 하위 트리이지만 데이터 구조 의미에서는 하위 노드가 없습니다.
레퍼런스
- ^ Weisstein, Eric W. "Subtree". MathWorld.
- ^ Susanna S. Epp (Aug 2010). Discrete Mathematics with Applications. Pacific Grove, CA: Brooks/Cole Publishing Co. p. 694. ISBN 978-0-495-39132-6.
- ^ Donald Knuth (1997). "Section 2.3.4.2: Oriented trees". The Art of Computer Programming. Vol. 1: Fundamental Algorithms (Third ed.). Addison-Wesley. p. 373.
- ^ L. Afanasiev; P. Blackburn; I. Dimitriou; B. Gaiffe; E. Goris; M. Marx; M. de Rijke (2005). "PDL for ordered trees" (PDF). Journal of Applied Non-Classical Logics. 15 (2): 115–135. doi:10.3166/jancl.15.115-135. S2CID 1979330.
추가 정보
- 도널드 크누트.컴퓨터 프로그래밍 기술: 기초 알고리즘, 제3판애디슨 웨슬리, 1997년ISBN 0-201-89683-4. 섹션 2.3: 나무, 페이지 308-423.
- 토마스 H. 코먼, 찰스 E. 리저슨, 로널드 L. 리베스트, 클리포드 스타인.알고리즘 소개, 제2판MIT Press and McGraw-Hill, 2001.ISBN 0-262-03293-7.섹션 10.4: 뿌리 나무의 표현, 페이지 214–217.12~14장 (이진 검색 트리, 빨간색-검은색 트리, 데이터 구조 증가), 페이지 253–320.
외부 링크
- 2013년 8월 8일 Sally Knipe가 발표한 복합 데이터 분석 수단으로서의 데이터 트리
- 알고리즘 및 데이터 구조 사전의 설명
- CRAN 패키지 data.tree – R 프로그래밍 언어로 트리 데이터 구조 구현
- WormWeb.org: C. elegans 세포 트리의 인터랙티브 시각화– 선충 C. elegans 세포 계보 트리 전체를 시각화한다(creascript).
- L의 바이너리 트리앨리슨