머저리나무

그래프 이론에서 m-ary 트리(음이 아닌 정수 m의 경우)(n-ary, k-ary 또는 k-way tree라고도 함)는 각 노드에 m개 이하의 자식이 있는 수목(또는 일부 저자의 경우 순서가 지정된 트리)^[1]^[2]입니다.이진 트리는 m = 2인 특수한 경우이고, 삼원 트리는 자식을 세 개로 제한하는 m = 3인 또 다른 경우입니다.

m-ary tree의 종류

전체 m-ary 트리는 각 수준 내의 모든 노드에 0개 또는 m개의 자식이 있는 m-ary 트리입니다.
완전한 m-ary^[3]^[4] 트리(또는 덜 일반적으로 완전한 m-ary^[5] 트리)는 모든 잎 노드가 동일한 깊이에 있는 완전한 m-ary 트리입니다.

m-ary tree의 특성

높이가 h인 m-ary 트리의 경우 최대 잎 수의 상한은 $m^{h}$ {\ $displaystyle$ m $^{h$ 입니다.
m-ary 트리의 높이 h는 루트 노드를 포함하지 않으며, 높이가 0인 루트 노드만 포함하는 트리입니다.
트리의 높이는 트리에 있는 노드의 최대 깊이 D와 같습니다.
완벽한 m-ary 트리의 ${\displaystyle$ N $}$ $N$ 수는 ∑ ${\textstyle \sum _{i=0}^{h}m^{i}={\frac {m^{h+1}-1}{m-1}}}$ = ${\textstyle \sum _{i=0}^{h}m^{i}={\frac {m^{h+1}-1}{m-1}}}$ ${\textstyle \sum _{i=0}^{h}m^{i}={\frac {m^{h+1}-1}{m-1}}}$ ${\textstyle \sum _{i=0}^{h}m^{i}={\frac {m^{h+1}-1}{m-1}}}$ i = ${\textstyle \sum _{i=0}^{h}m^{i}={\frac {m^{h+1}-1}{m-1}}}$ h + ${\textstyle \sum _{i=0}^{h}m^{i}={\frac {m^{h+1}-1}{m-1}}}$ - ${\textstyle \sum _{i=0}^{h}m^{i}={\frac {m^{h+1}-1}{m-1}}}$ ${\textstyle \sum _{i=0}^{h}m^{i}={\frac {m^{h+1}-1}{m-1}}}$ - 1 ${\textstyle \sum _{i=0}^{h}m^{i}={\frac {m^{h+1}-1}{m-1}}}$ {\ $textstyle \sum$ _ ${i$ = $0}^{h}m^{i$ }={\ $frac {m^{h+1}-1}{m-1}}$ 입니다 ${\textstyle \sum _{i=0}^{h}m^{i}={\frac {m^{h+1}-1}{m-1}}}$

{\begin{aligned}&{\frac {m^{h+1}-1}{m-1}}\geq N>{\frac {m^{h}-1}{m-1}}\[8pt]&m^{h+1}\geq(m-1)\cdot N+1>m^{h}\[8pt]&h+1\geq \log _{m}\left(m-1)\cdot N+1\right)>h\[8pt]&h\geq \left\lceil \log _{m}(m-1)\cdot N+1)-1\right\rceil .\end{aligned}

Big-Ω 의 정의에 따라 최대 깊이

D=h\geq \left\lceil \log _{m}((m-1))\cdot N+1)-1\rceil =O(\log _{m}n)=O(\log n/\log m)

n개의 노드가 있는 완전한 m-ary 트리의 ${\textstyle \lfloor \log _{m}((m-1)\cdot n)\rfloor }$ 는 ⌊ ${\textstyle \lfloor \log _{m}((m-1)\cdot n)\rfloor }$ m ⁡ ${\textstyle \lfloor \log _{m}((m-1)\cdot n)\rfloor }$ ( ( ${\textstyle \lfloor \log _{m}((m-1)\cdot n)\rfloor }$ - ${\textstyle \lfloor \log _{m}((m-1)\cdot n)\rfloor }$ ) ⋅ ${\textstyle \lfloor \log _{m}((m-1)\cdot n)\rfloor }$ ) ⌋ {\ $textstyle \lfloor \log$ _ ${m}$ ( ( $m-1)\cdot$ n )\ $rfloor$ ${\textstyle \lfloor \log _{m}((m-1)\cdot n)\rfloor }$ 입니다.
노드가 n개인 가능한 m-ary 트리의 총 ${\textstyle C_{n}={\frac {1}{(m-1)n+1}}\cdot {\binom {m\cdot n}{n}}}$ 는 ${\textstyle C_{n}={\frac {1}{(m-1)n+1}}\cdot {\binom {m\cdot n}{n}}}$ n = ${\textstyle C_{n}={\frac {1}{(m-1)n+1}}\cdot {\binom {m\cdot n}{n}}}$ ( ${\textstyle C_{n}={\frac {1}{(m-1)n+1}}\cdot {\binom {m\cdot n}{n}}}$ - ${\textstyle C_{n}={\frac {1}{(m-1)n+1}}\cdot {\binom {m\cdot n}{n}}}$ ) ${\textstyle C_{n}={\frac {1}{(m-1)n+1}}\cdot {\binom {m\cdot n}{n}}}$ + ${\textstyle C_{n}={\frac {1}{(m-1)n+1}}\cdot {\binom {m\cdot n}{n}}}$ ⋅ ( ${\textstyle C_{n}={\frac {1}{(m-1)n+1}}\cdot {\binom {m\cdot n}{n}}}$ ⋅ ${\textstyle C_{n}={\frac {1}{(m-1)n+1}}\cdot {\binom {m\cdot n}{n}}}$ ) ${\textstyle C_{n}={\frac {1}{(m-1)n+1}}\cdot {\binom {m\cdot n}{n}}}$ {\ $textstyle$ C_ ${n$ }={\ $frac {1}{(m-1)n+1}}\cdot$ {\ $binom {m\cdot$ n $}{n}($ 카탈란 숫자)입니다.

m-ary 트리의 횡단방법

m진 트리를 횡단하는 것은 이진 트리를 횡단하는 것과 매우 유사합니다.사전 순서 횡단은 부모, 왼쪽 하위 트리 및 오른쪽 하위 트리로 이동하며, 사후 순서 횡단의 경우 왼쪽 하위 트리, 오른쪽 하위 트리 및 부모 노드로 이동합니다.순서대로 횡단하려면 m > 2의 노드당 두 개 이상의 자식이 있으므로 왼쪽 및 오른쪽 하위 트리의 개념을 정의해야 합니다.왼쪽/오른쪽 하위 트리를 설정하는 일반적인 방법은 자식 노드 목록을 두 그룹으로 나누는 것입니다.노드의 m개 자식에 순서를 정의하면 첫 번째 { ${\textstyle \{1,\dots ,\lfloor {\frac {m}{2}}\rfloor \}}$ ${\textstyle \{1,\dots ,\lfloor {\frac {m}{2}}\rfloor \}}$ ⌊ ${\textstyle \{1,\dots ,\lfloor {\frac {m}{2}}\rfloor \}}$ ${\textstyle \{1,\dots ,\lfloor {\frac {m}{2}}\rfloor \}}$ ⌋ ${\textstyle \{1,\dots ,\lfloor {\frac {m}{2}}\rfloor \}}$ {\ $textstyle$ \{ $1,\dots,\lfloor$ {\ $frac {m}{2}}\rfloor$ \} 노드는 왼쪽 하위 트리를 구성하고 { ${\textstyle \{\lceil {\frac {m}{2}}\rceil ,\dots ,m\}}$ ⌈ ${\textstyle \{\lceil {\frac {m}{2}}\rceil ,\dots ,m\}}$ ${\textstyle \{\lceil {\frac {m}{2}}\rceil ,\dots ,m\}}$ ⌉ ${\textstyle \{\lceil {\frac {m}{2}}\rceil ,\dots ,m\}}$ …, ${\textstyle \{\lceil {\frac {m}{2}}\rceil ,\dots ,m\}}$ ${\textstyle \{\lceil {\frac {m}{2}}\rceil ,\dots ,m\}}$ {\ $textstyle \{\lceil$ {\ $frac {m}{2}}\rceil ,\dots,m\}$ 노드는 오른쪽 하위 트리를 구성합니다.

m-ary 트리를 이진 트리로 변환

실제 응용프로그램의 노드 대부분이 m개 미만의 자식을 포함하고 있으므로 m개의 트리를 표현하기 위해 배열을 사용하는 것은 비효율적입니다.결과적으로, 이 사실은 메모리에 사용되지 않는 큰 공간을 갖는 희소 배열로 이어집니다.임의의 m-ary 트리를 이진 트리로 변환하면 트리의 높이가 일정한 인자만큼 증가할 뿐이며 전체 최악의 경우 시간 복잡도에 영향을 미치지 않습니다.즉 ${\textstyle O(\log _{m}n)\equiv O(\log _{2}n)}$ ${\textstyle \log _{2}m\cdot \log _{m}n={\frac {\log m}{\log 2}}\cdot {\frac {\log n}{\log m}}=\log _{2}n}$ 2 ⁡ ${\textstyle \log _{2}m\cdot \log _{m}n={\frac {\log m}{\log 2}}\cdot {\frac {\log n}{\log m}}=\log _{2}n}$ ⋅ ${\textstyle \log _{2}m\cdot \log _{m}n={\frac {\log m}{\log 2}}\cdot {\frac {\log n}{\log m}}=\log _{2}n}$ m ⁡ ${\textstyle \log _{2}m\cdot \log _{m}n={\frac {\log m}{\log 2}}\cdot {\frac {\log n}{\log m}}=\log _{2}n}$ ${\textstyle O(\log _{m}n)\equiv O(\log _{2}n)}$ ⁡ n ≡ ${\textstyle O(\log _{m}n)\equiv O(\log _{2}n)}$ ( ${\textstyle O(\log _{m}n)\equiv O(\log _{2}n)}$ 2 ⁡ ${\textstyle O(\log _{m}n)\equiv O(\log _{2}n)}$ ) ${\textstyle$ O (\ $log _{m}n)$ = ${\textstyle \log _{2}m\cdot \log _{m}n={\frac {\log m}{\log 2}}\cdot {\frac {\log n}{\log m}}=\log _{2}n}$ ⁡ m ${\textstyle \log _{2}m\cdot \log _{m}n={\frac {\log m}{\log 2}}\cdot {\frac {\log n}{\log m}}=\log _{2}n}$ ⁡ $2$ ⋅ ${\textstyle \log _{2}m\cdot \log _{m}n={\frac {\log m}{\log 2}}\cdot {\frac {\log n}{\log m}}=\log _{2}n}$ ⁡ ${\textstyle \log _{2}m\cdot \log _{m}n={\frac {\log m}{\log 2}}\cdot {\frac {\log n}{\log m}}=\log _{2}n}$ ${\textstyle \log _{2}m\cdot \log _{m}n={\frac {\log m}{\log 2}}\cdot {\frac {\log n}{\log m}}=\log _{2}n}$ ⁡ m = ${\textstyle \log _{2}m\cdot \log _{m}n={\frac {\log m}{\log 2}}\cdot {\frac {\log n}{\log m}}=\log _{2}n}$ 2 ⁡ ${\textstyle \log _{2}m\cdot \log _{m}n={\frac {\log m}{\log 2}}\cdot {\frac {\log n}{\log m}}=\log _{2}n}$ {\ $textstyle \log$ _ ${2}m\cdot$ \ $log$ _ ${m}n$ ={\ $frac$ {\ $log$ m $}{\log 2}}\cdot {\$ frac {\ $log$ m $}{\$ log m}}=\ $log$ _ ${2}n$

먼저, 우리는 링크 리스트를 형성하기 위해 주어진 부모 노드의 모든 직계 자식 노드를 함께 연결합니다.그런 다음 부모에서 첫째(즉, 가장 왼쪽) 자녀로 연결되는 링크를 유지하고 나머지 자녀로 연결되는 다른 링크를 모두 제거합니다.모든 내부 노드를 처리하고 트리를 시계 방향으로 45도 회전시킬 때까지 모든 어린이(자녀가 있는 경우)에 대해 이 과정을 반복합니다.얻은 트리는 주어진 m-ary 트리에서 얻은 원하는 이진 트리입니다.

m-ary tree 저장방법

배열

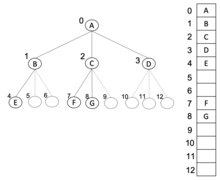
m-ary 트리는 배열에서 암시적인 데이터 구조로서 너비 우선 순서로 저장될 수도 있으며, 트리가 완전한 m-ary 트리인 경우 이 방법은 공간을 낭비하지 않습니다.이 콤팩트 배열에서 노드에 인덱스 i가 있는 경우 범위 {1,…,m}에 있는 c번째 $m\cdot i+c$ 은 인덱스 $m\cdot i+c$ ⋅ i + $m\cdot i+c$ c {\ $displaystyle m\cdot i+$ c $m\cdot i+c$ 에 있는 반면, 부모(있는 경우)는 ${\textstyle \left\lfloor {\frac {i-1}{m}}\right\rfloor }$ ⌊ ${\textstyle \left\lfloor {\frac {i-1}{m}}\right\rfloor }$ - 1 $m$ ⌋ $\left$ \textstyle {\ $frac {i-1}{m}}\right\rfloor$ }(루트에 인덱스 0이 있다고 가정)에 있습니다.이 방법은 특히 사전 주문 순회 중에 보다 컴팩트한 저장 공간과 보다 정확한 참조 위치를 제공합니다.이 메서드의 공간 복잡도는 O $O(m^{n})$ {\ $displaystyle$ O $(m^{n$ 입니다.

포인터 기반

각 노드에는 $m개$ ${\displaystyle$ m $}$ 개의 $m$ 자식 각각에 대한 포인터를 저장하는 내부 어레이가 있습니다.

배열 기반 구현에 비해 이 구현 방법은 O $O(m\cdot n)$ ⋅ n $O(m\cdot n)$ ${\displaystyle$ O $(m\cdot$ n $O(m\cdot n)$ 의 공간 복잡도가 우수합니다.

m-ary 트리의 열거

가능한 모든 m-ary 트리를 나열하는 것은 가설 또는 이론을 확인하는 방법으로 많은 학문 분야에서 유용합니다.m-ary 트리 객체를 적절히 표현하면 생성 과정을 크게 단순화할 수 있습니다.이진 값을 사용하여 주어진 인덱스에서 노드의 존재를 나타내는 n개의 노드를 갖는 m-ary 트리의 깊이 우선 검색을 사용하여 비트 시퀀스 표현을 구성할 수 있습니다.예를 들어, 비트 시퀀스 x=1110000100010001000은 아래와 같이 n=6개의 노드를 가진 3-ary 트리를 나타냅니다.

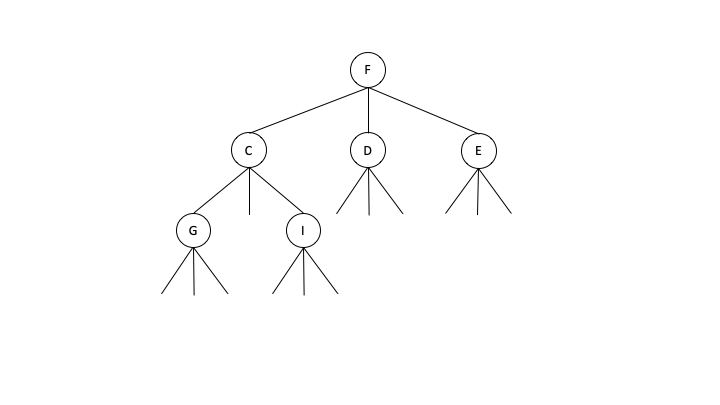
3-ary tree with bit sequence of 1110000100010001000 and Simple Zero Sequence of 004433 — 비트 시퀀스가 *1110000100010001000*이고 단순 영점 시퀀스가 *004433인* 3-ary 트리

이 표현의 문제점은 모든 비트 문자열을 사전식 순서대로 나열하면 연속되는 두 개의 문자열이 사전식으로 매우 다른 두 개의 트리를 나타낼 수 있다는 것을 의미합니다.따라서 이진 문자열에 대한 열거가 반드시 모든 m-ary ^[7]트리의 순서대로 생성되는 것은 아닙니다.더 나은 표현은 단순 영점 시퀀스라고 알려진 연속적인 영점 사이의 영점 수를 나타내는 정수 문자열을 기반으로 합니다. ${\textstyle S=s_{1},s_{2},\dots ,s_{n-1}}$ $=$ ${\textstyle S=s_{1},s_{2},\dots ,s_{n-1}}$ 1 ${\textstyle S=s_{1},s_{2},\dots ,s_{n-1}}$ ${\textstyle S=s_{1},s_{2},\dots ,s_{n-1}}$ 2 ${\textstyle S=s_{1},s_{2},\dots ,s_{n-1}}$ ${\textstyle S=s_{1},s_{2},\dots ,s_{n-1}}$ ${\textstyle S=s_{1},s_{2},\dots ,s_{n-1}}$ ${\textstyle S=s_{1},s_{2},\dots ,s_{n-1}}$ - 1 ${\textstyle S=s_{1},s_{2},\dots ,s_{n-1}}$ {\ $textsty$ S= $s_{1}, s_{2},\dots,s_{n-1}}$ 는 비트 ${\textstyle 10^{s_{1}}10^{s_{2}}\ldots 10^{s_{n-1}}10^{j}}$ ${\textstyle 10^{s_{1}}10^{s_{2}}\ldots 10^{s_{n-1}}10^{j}}$ s ${\textstyle 10^{s_{1}}10^{s_{2}}\ldots 10^{s_{n-1}}10^{j}}$ ${\textstyle 10^{s_{1}}10^{s_{2}}\ldots 10^{s_{n-1}}10^{j}}$ s ${\textstyle 10^{s_{1}}10^{s_{2}}\ldots 10^{s_{n-1}}10^{j}}$ … ${\textstyle 10^{s_{1}}10^{s_{2}}\ldots 10^{s_{n-1}}10^{j}}$ s ${\textstyle 10^{s_{1}}10^{s_{2}}\ldots 10^{s_{n-1}}10^{j}}$ n - ${\textstyle 10^{s_{1}}10^{s_{2}}\ldots 10^{s_{n-1}}10^{j}}$ j {\ $textstyle$ 10 $^{s_{1$ }}, $10^{s_{$ 2}}, ldots $10^{s_{n-1}, 10^{$ j}, 여기서 j는 문자열이 적절한 길이를 갖도록 하기 위해 시퀀스의 끝에 필요한 0의 개수입니다.예를 들어, $1110000100010001000\equiv 10^{0}10^{0}10^{4}10^{4}10^{3}\equiv 00433$ 1000 ≡ $1110000100010001000\equiv 10^{0}10^{0}10^{4}10^{4}10^{3}\equiv 00433$ $1110000100010001000\equiv 10^{0}10^{0}10^{4}10^{4}10^{3}\equiv 00433$ $1110000100010001000\equiv 10^{0}10^{0}10^{4}10^{4}10^{3}\equiv 00433$ $1110000100010001000\equiv 10^{0}10^{0}10^{4}10^{4}10^{3}\equiv 00433$ 4 $1110000100010001000\equiv 10^{0}10^{0}10^{4}10^{4}10^{3}\equiv 00433$ $1110000100010001000\equiv 10^{0}10^{0}10^{4}10^{4}10^{3}\equiv 00433$ 3 ≡ $1110000100010001000\equiv 10^{0}10^{0}10^{4}10^{4}10^{3}\equiv 00433$ {\ $displaystyle 111000010001000$ 1000\ $equiv 10$ ^{ $0}$ 10 $^{0}10^{4}10^{3$ }\ $equiv$ 00433 $}$ 은 위 그림의 단순 제로 시퀀스 표현입니다.00433을 좀 더 압축적으로 표현하면 $0^{2}4^{1}3^{2}$ 2 4 $0^{2}4^{1}3^{2}$ $0^{2}4^{1}3^{2}$ $0^{2}4^{1}3^{2}$ {\ $displaystyle$ 0 $^{2}4^{1}3^{2$ 이며, 중복되는 베이스는 인접할 수 없습니다.이 새 표현을 사용하면 O $O(1)$ ${\displaystyle$ O $(1$ 에서 다음 유효한 시퀀스를 구성할 수 있습니다. 다음과 같은 경우 간단한 영(0) 시퀀스가 유효합니다.

\sum _{i=1}^{i=j}s_{i}\leq (m-1)j\qquad \for all j\leq n-1.

즉, m-ary 트리의 비트 시퀀스에서 0의 수는 null 포인터(즉, 자식 노드가 연결되지 않은 포인터)의 총 수를 초과할 수 없습니다.이 합은 n

n-1

-

n-1

{\

displaystyle n-1}

개의

n-1

n-1

에 제한을 가하고 있으므로 잘못된 구조(예:

n^{t}h

노드를 연결하는 데 사용 가능한 null 포인터 포함)를

n^{t}h

않고 n번째

n^{t}h

{\

displaystyle

n

^{t}h}

개의

n^{t}h

노드를 추가할 수 있는 여지가 있습니다.

아래 표는 노드가 4개인 모든 3-ary 트리의 유효한 단순 0 시퀀스 목록을 보여 줍니다.

222	200	111	033	013
221	132	110	032	012
220	131	105	031	011
213	130	104	030	010
212	123	103	024	006
211	122	102	023	005
210	121	101	022	004
204	120	100	021	003
203	114	042	020	002
202	113	041	015	001
201	112	040	014	000

테이블의 오른쪽 하단(즉, "000")부터 시작하여 "000"부터 "006"까지 가능한 순서 트리의 생성을 제어하는 백본 템플릿이 있습니다.이 그룹("00X")의 백본 템플릿은 아래에 나와 있으며, 여기서 "x"라는 레이블이 붙은 위치에 노드가 추가됩니다.

백본 템플릿에서 가능한 모든 위치를 다 사용하면 아래에 나와 있는 것처럼 세 번째 노드의 한 위치를 오른쪽으로 이동하여 새 템플릿을 구성하고 "X"라는 레이블이 지정된 모든 위치를 다 사용할 때까지 동일한 열거가 수행됩니다.

m = $m=3$ {\ $displaystyle$ m= $3},$ $n=4$ = $n=4$ {\ $displaystyle$ n= $4$ 인 모든 m-ary 트리의 열거 테이블로 돌아가 보면, "006"에서 "010"으로의 명백한 점프는 다음과 같이 알고리즘적인 방식으로 사소한 방식으로 설명될 수 있습니다.

이 열거에 대한 의사 코드는 ^[7]다음과 같습니다.

절차 NEXT (s, s, …, s) 만약 s = 0이면 i ← max {is > 0} s ← i < n - 1이면 s ← (i + 1) ⋅ (m - 1) - j ← i + 2, i + 3, …, n - 1s ← k - 1 end이면 종료

무루프 열거법

O $O(1)$ ( $O(1)$ ${\displaystyle$ O $(1)}$ 최악의 $O(1)$ 시간을 $O(1)$ 생성 알고리즘은 시간 복잡도가 루프 또는 재귀를 포함할 수 없기 때문에 루프리스라고 불립니다.초기화 후 O $O(1)$ {\ $displaystyle$ O $(1$ 에 연속적인 트리 개체를 생성하는 경우 m-ary 트리에 대한 루프리스 열거는 루프리스라고 합니다. ${\displaystyle$ a $}$ 이 $a$ (가) 노드 중 $d$ 이고d {\ $displaystyle$ d $}이($ ) t {\displaystyle t}번째 $d$ $t$ 자식인 $a$ 된 m-ary 트리 T에 대해 다음을 수행하여 ${\displaystyle$ a $}$ 의 $a$ 왼쪽 t 회전을 수행합니다.d{\ $displaystyle$ d $}$ 이 $d$ (가) 루트 노드이고 $,$ b {\ $displaystyle$ b $}$ 과 $b$ (와) 모든 하위 $트리$ 를 {\ $displaystyle$ }의 하위 트리로 만듭니다. $m-1$ 로 $m-1$ m $m-1$ - 1 {\ $displaystyle$ $m-1$ m-1 $m-1$ $}$ 의 왼쪽 대부분의 하위 $트리$ 를 {\ $displaystyle$ }개에 할당하고 $,$ d {\ $displaystyle$ d}개의 $d$ 오른쪽 가장 $하위$ 트리는 {\ $displaystyle$ d $}$ $d$ 로 $d$ 승격되는 동안에도 연결된 상태를 $유지$ 합니다.다음과 같이 root:

i = 1...n에 대해 m진 트리를 왼쪽 트리로 변환: t = 2...m에 대해: 깊이 i ≥ 1에 있는 노드의 자식: 깊이 i end에 있는 노드에서 L-t 회전하는 동안 끝에서 끝까지

d에서 오른쪽 t 회전은 이 연산의 역입니다.T의 왼쪽 체인은 $x_{1},x_{2},\dots ,x_{n}$ 1 $,$ $x_{1},x_{2},\dots ,x_{n}$ $x_{1},x_{2},\dots ,x_{n}$ …, $x_{1},x_{2},\dots ,x_{n}$ n $x_{1},x_{2},\dots ,x_{n}$ {\ $displaystyle x_{1}, x_{2},\dots, x_{n}}$ 개 $x_{1},x_{2},\dots ,x_{n}$ 노드로 $x_{1}$ 시퀀스이며, $x_{n}$ n {\ $displaystyle x_{$ n $x_{1}$ $x_{n}$ } $x_{n}$ 를 제외한 모든 노드는 왼쪽 포인터에 하나의 자식을 연결합니다( $m[1]$ m [ $m[1]$ {\ $displaystyle$ m $[1$ 모든 m-ary 트리는 2에서 m까지의 유한한 왼쪽-t 회전 시퀀스를 사용하여 왼쪽 체인 트리로 변환될 수 있습니다.특히 각 깊이에서 $m-1$ m - $m-1$ {\ $displaystyle m-1}$ 하위 $m-1$ 트리가 null이 될 때까지 각 $x_{i}$ $x_{i}$ {\ $displaystyle x_{i}$ 에 $x_{i}$ 대해 왼쪽 회전을 수행하여 이 작업을 수행할 수 있습니다.그러면, $c_{i}$ ${\$ 로 $c_{i}$ 표시되는 깊이에서 수행되는 좌회전 횟수의 순서는 동일한 우회전 순서를 수행함으로써 회복될 수 있는 m-ary 트리의 코드워드를 정의합니다.

$c_{1},c_{2},\dots ,c_{m-1}$ 1 $c_{1},c_{2},\dots ,c_{m-1}$ $c_{1},c_{2},\dots ,c_{m-1}$ $c_{1},c_{2},\dots ,c_{m-1}$ $c_{1},c_{2},\dots ,c_{m-1}$ $c_{1},c_{2},\dots ,c_{m-1}$ - $c_{1},c_{2},\dots ,c_{m-1}$ {\ $displaystyle$ $c_$ {1}, $c_{2},\$ displaystyle $c_{2},\display,c_{m-1}}$ $m-1$ L-2 회전 수, L-3 회전 수, ..., 근에서 발생한 L-m 회전 수(즉, i=1)를 나타내도록 합니다.그러면 c $c_{(i-1)(m-1)+t-1}$ ( $c_{(i-1)(m-1)+t-1}$ - $c_{(i-1)(m-1)+t-1}$ ) ( $c_{(i-1)(m-1)+t-1}$ - $c_{(i-1)(m-1)+t-1}$ ) + $c_{(i-1)(m-1)+t-1}$ - 1 $c_{(i-1)(m-1)+t-1}$ {\ $displaystyle c_{(i-1)$ ( $m-1)$ + $t-1}}$ 는 $c_{(i-1)(m-1)+t-1}$ 깊이 i에서 필요한 L-t 회전 수이 됩니다.

각 깊이에서 왼쪽 회전 횟수를 캡처하는 것은 m-ary 트리를 인코딩하는 방법입니다.따라서 가능한 모든 법적 인코딩을 열거하면 주어진 m과 n에 대한 모든 m-ary 트리를 생성하는 데 도움이 될 것입니다.그러나 m개의 음이 아닌 정수의 모든 $c_{i}$ {\ $displaystyle c_{i}$ 개 $c_{i}$ 시퀀스가 유효한 m-ary 트리를 나타내는 것은 아닙니다.(n - $(n-1)\cdot (m-1)+1$ ⋅ ( $(n-1)\cdot (m-1)+1$ - $(n-1)\cdot (m-1)+1$ ) + $(n-1)\cdot (m-1)+1$ {\ $displaystyle (n-1)\cdot (m-1)+1}$ 개의 음이 아닌 정수의 $(n-1)\cdot (m-1)+1$ 수열은 다음과 같은 경우에만 유효한 m-ary 트리 표현입니다.

\sum _{i=j}^{n}\sum _{t=2}^{m}c_{(i-1)(m-1)+t-1}\qquad \leq n-j,\qquad \for all j\in 0\n.

n개의 노드를 가진 m-ary의 사전적으로 가장 작은 코드워드 표현은 모두 0이고 가장 큰 것은 n-1이고 오른쪽에 m-1 0이 뒤따릅니다.

1부터 n⋅(k - 1)까지의 모든 i에 대해 초기화 c[i]를 0으로 설정 p[i]에서 1부터 n까지의 i에 대해 n - 1로 설정 ← 0 j ← m - 1 종료 조건 c[1] = n - 1 프로시저 NEXT 합계 ← 합계 + 1 - c[j + 1] c[j] ← c[j] + 1 인 경우 p[q[j] + 1 인 경우 p[q[j] ← p[j + c[j]] ← p[q[j] + c[j]] ← p[q[j] + 1 인 경우 p[q[j] = 0 if sum ← p[q[j]] 인 경우 j  j j− 1 다른 p[n] ← 합 j ← m - 끝인 경우 1 end

어플

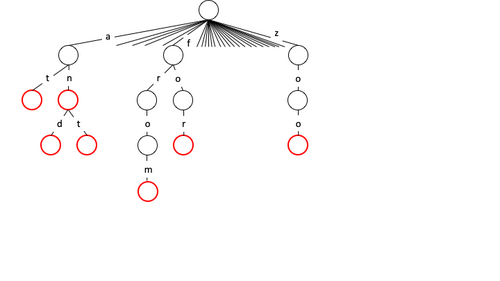
m-ary 트리의 응용 프로그램 중 하나는 허용 가능한 문자열의 유효성 검사를 위한 사전을 만드는 것입니다.이를 위해서는 시작점을 나타내는 트리의 루트가 있는 유효한 알파벳의 수(예를 들어 영어 알파벳의 문자 수)와 같게 해야 합니다.마찬가지로 각 자식은 문자열에서 다음으로 가능한 문자를 나타내는 자식을 최대 m까지 가질 수 있습니다.따라서 경로를 따라 있는 문자는 키의 끝 문자를 "말단 노드"로 표시하여 유효한 키를 나타낼 수 있습니다.예를 들어, 아래 예에서 "at" 및 "and"는 터미널 노드로 표시된 "t" 및 "d"의 유효한 키 문자열입니다.터미널 노드는 지정된 키에 연결할 추가 정보를 저장할 수 있습니다.B-tree, Octree 및/또는 trie를 사용하여 이러한 사전을 구축하는 유사한 방법이 있습니다.

참고 항목

참고문헌

^ Li, Liwu (1998). Java: Data Structures and Programming. Section 8.1.2.1, Multi-Ary Trees: Springer. doi:10.1007/978-3-642-95851-9. ISBN 978-3-642-95853-3. S2CID 708416. Retrieved 20 July 2023.{{cite book}}: CS1 메인 : 위치 (링크)
^ Stanley, Richard P. (2011). Enumerative Combinatorics, Volume I. Appendix: Graph Theory Terminology: Cambridge University Press. p. 573. ISBN 978-1-107-60262-5. Retrieved 20 July 2023.
^ Gross, Jonathan L.; Yellen, Jay; Anderson, Mark (2018). Graph Theory and Its Applications (3rd ed.). Section 3.2, Rooted Trees, Ordered Trees, and Binary Trees: CRC Press. p. 132. ISBN 978-1-4822-4948-4.{{cite book}}: CS1 메인 : 위치 (링크)
^ Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2022). Introduction to Algorithms (4th ed.). Section B.5.3, Binary and positional trees: MIT Press. p. 1174. ISBN 9780262046305. Retrieved 20 July 2023.{{cite book}}: CS1 메인 : 위치 (링크)
^ Schumacher, Patrik (2012). "Excursion: Network Theory". The Autopoiesis of Architecture: A New Agenda for Architecture, Vol. II. Wiley. p. 103. ISBN 978-0-470-66616-6.
^ Graham, Ronald L.; Knuth, Donald E.; Patashnik, Oren (1994). Concrete Mathematics: A Foundation for Computer Science (2nd ed.). AIP.
^ ^a ^b Baronaigien, Dominique Roelants van (2000). "Loop Free Generation of K-ary trees". Journal of Algorithms. 35 (1): 100–107. doi:10.1006/jagm.1999.1073.
^ ^a ^b Korsh, James F (1994). "Loopless generation of k-ary tree sequences". Information Processing Letters. Elsevier. 52 (5): 243–247. doi:10.1016/0020-0190(94)00149-9.

Storer, James A. (2001). An Introduction to Data Structures and Algorithms. Birkhäuser Boston. ISBN 3-7643-4253-6.

외부 링크

N-ary tree, Bruno R.프리즈, 박사, 피엔.

[1] Li, Liwu (1998). Java: Data Structures and Programming. Section 8.1.2.1, Multi-Ary Trees: Springer. doi:10.1007/978-3-642-95851-9. ISBN 978-3-642-95853-3. S2CID 708416. Retrieved 20 July 2023.{{cite book}}: CS1 메인 : 위치 (링크)

[2] Stanley, Richard P. (2011). Enumerative Combinatorics, Volume I. Appendix: Graph Theory Terminology: Cambridge University Press. p. 573. ISBN 978-1-107-60262-5. Retrieved 20 July 2023.

[3] Gross, Jonathan L.; Yellen, Jay; Anderson, Mark (2018). Graph Theory and Its Applications (3rd ed.). Section 3.2, Rooted Trees, Ordered Trees, and Binary Trees: CRC Press. p. 132. ISBN 978-1-4822-4948-4.{{cite book}}: CS1 메인 : 위치 (링크)

[4] Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2022). Introduction to Algorithms (4th ed.). Section B.5.3, Binary and positional trees: MIT Press. p. 1174. ISBN 9780262046305. Retrieved 20 July 2023.{{cite book}}: CS1 메인 : 위치 (링크)

[5] Schumacher, Patrik (2012). "Excursion: Network Theory". The Autopoiesis of Architecture: A New Agenda for Architecture, Vol. II. Wiley. p. 103. ISBN 978-0-470-66616-6.

[6] Graham, Ronald L.; Knuth, Donald E.; Patashnik, Oren (1994). Concrete Mathematics: A Foundation for Computer Science (2nd ed.). AIP.

[looplessgeneration-7] Baronaigien, Dominique Roelants van (2000). "Loop Free Generation of K-ary trees". Journal of Algorithms. 35 (1): 100–107. doi:10.1006/jagm.1999.1073.

[karyrotationgeneration-8] Korsh, James F (1994). "Loopless generation of k-ary tree sequences". Information Processing Letters. Elsevier. 52 (5): 243–247. doi:10.1016/0020-0190(94)00149-9.

[1]

[2]

[3]

[4]

[5]

[7]

v t 트리 데이터 구조
트리 검색 (동적 집합/연관 배열)	2–3 2–3–4 AA (a,b) AVL B B+ B* 나^x (최적) 이항 검색 댄싱 하트리 간격 주문통계 (좌측기울기) 레드-블랙 희생양 스플레이 T 트랩 UB 무게균형
수북이	이진법 이항법 브로달 피보나치 레프트 페어링 스큐 반 엠데 보아스 약한
시도하다	크트리 C-trie(압축 ADT) 해시 라딕스 접미사 삼차 탐색 엑스패스트 와이패스트
공간 데이터 분할 트리	공 BK BSP 데카르트 힐베르트 R k-d(최소 k-d) M 미터법 MVP 옥트리 PH 우선순위 R 쿼드 R R+ R* 부분 부사장 X
기타나무	덮다 지수 펜윅 손가락. 프랙탈 트리 색인 퓨전 해시 캘린더 아이디스턴스 케이아리 좌충우돌 링크/컷 로그 구조 병합 머클 p q. 범위 SPQR 정상

Search